Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Alireza Gorjian
 -- 2829 2023-03-21 18:05:21 |
2 Reference format revised.
Lindsay Dong
+ 194 word(s) 3023 2023-03-22 01:48:25 |

Video Upload Options

Do you have a full video?
Send video materials Upload full video

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Gorjian, A.; Eskandari, M.; Moradi, M.H. Conservation Voltage Reduction in Modern Power Systems. Encyclopedia. Available online: https://encyclopedia.pub/entry/42402 (accessed on 27 July 2024).
Gorjian A, Eskandari M, Moradi MH. Conservation Voltage Reduction in Modern Power Systems. Encyclopedia. Available at: https://encyclopedia.pub/entry/42402. Accessed July 27, 2024.
Gorjian, Alireza, Mohsen Eskandari, Mohammad H. Moradi. "Conservation Voltage Reduction in Modern Power Systems" Encyclopedia, https://encyclopedia.pub/entry/42402 (accessed July 27, 2024).
Gorjian, A., Eskandari, M., & Moradi, M.H. (2023, March 21). Conservation Voltage Reduction in Modern Power Systems. In Encyclopedia. https://encyclopedia.pub/entry/42402
Gorjian, Alireza, et al. "Conservation Voltage Reduction in Modern Power Systems." Encyclopedia. Web. 21 March, 2023.
Conservation Voltage Reduction in Modern Power Systems
Edit
This entry is adapted from the peer-reviewed paper 10.3390/en16052502

Conservation voltage reduction (CVR) is a potentially effective and efficient technique for inertia synthesis and frequency support in modern grids comprising power electronics (PE)-based components, aiming to improve dynamic stability. In conventional power systems with synchronous generators, CVR utilization strategies aiming to conserve energy are split into two broad categories namely, open-loop and closed-loop techniques. Electromechanical voltage regulating devices, such as on-load tap changers (OLTCs), line drop compensators, and capacitor banks, are used to utilize CVR through open-loop procedures without measuring the voltage as a feedback signal. 

AI conservation voltage reduction (CVR) dynamics frequency support

1. Introduction

The stability of power systems should be preserved from various time scales, such as steady-state operation, dynamics, and faults transients, in each of which stability requirement should be achieved [1]. In this light, maintaining the balance between power production and consumption is the key factor. For example, from dynamics point view, instant balance should be held at the time scale of less than to a few seconds in power electronics (PE)-based modern grids. However, stabilizing PE-interfaced modern grids comprising inverter-interfaced distributed generation units (IIDGs) is challenging due to the multiple time scales of the control system of inverters. In addition, the high penetration of intermittent renewable energy sources (RESs) imposes more uncertainties to the grid which makes the stabilization scheme more complicated and more expensive [2].
The conservation voltage reduction (CVR) technique, which conventionally is used for peak shaving and demand reduction [3], can be an alternative/complementary solution for improving the dynamics stability. CVR is implemented by reducing the grid voltage which results in a reduction in power consumption based on the load-voltage sensitivity (LVS) [4]. Meanwhile, by controlling the voltage at the lower end of the voltage tolerance limit in dynamics, and consequently controlling the demanded active and reactive power, CVR can bring an instant balance in power production consumption at the dynamics time scale, resulting in improved grid stability. This is a remarkable achievement thanks to the fast response IIDGs provided that an appropriate control scheme for CVR is designed. Yet, CVR can also be a solution to economic and marketing problems by decreasing power consumption as a part of demand-side management programs in modern power systems.
Recently, CVR application in PE-based modern grids such as microgrids (MGs) comprising IIDGs has gained significant attention [5]. MGs are popular due to their high efficiency [6] and reliability in integrating IIDGs including RESs, BESSs, and smart loads (SLs) [7][8][9]. Further, the PE-based equipment is the key component, providing the necessary interface between the distributed energy resources (DERs), BESSs, and SLs to the grid [10]. However, the high penetration of PE interfaces and lack of physical inertia result in low inertia grids that consequently lead to critical frequency excursion and sharp dynamic instabilities [11]. CVR can be used as a frequency support approach in MGs with high IIDG penetration, providing the necessary inertia and subsequently addressing transient and dynamic instabilities. Hence, CVR increases the grid’s strength which prevents critical frequency deviations that consequently improve the flexibility and controllability of the micro sources (MSs) [12][13].

2. CVR Applications

2.1. CVR Performance and Principles

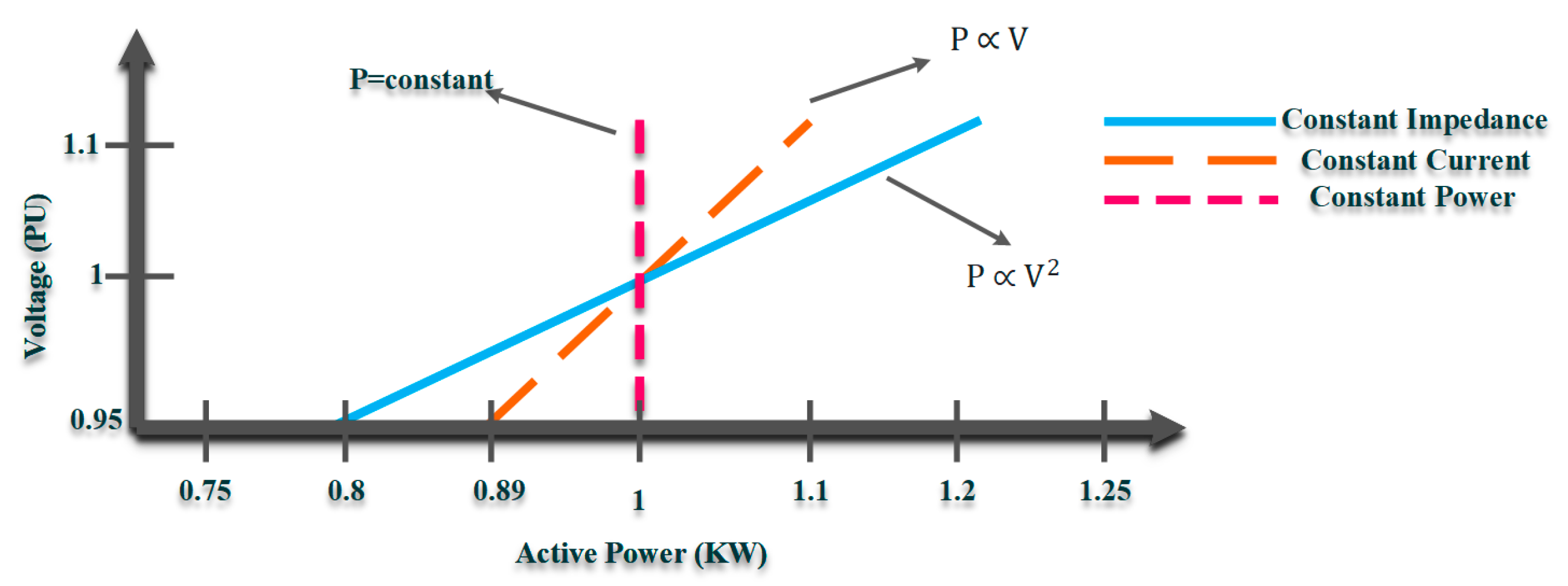
CVR is a low-cost, convenient, and straightforward technology used in power systems employing the basic rules of LVS. Due to the voltage dependency of the demanded active/reactive power, CVR can be adopted to regulate power consumption through LVS and by adjusting the voltage level (voltage Mag. and/or phase). The power flow of a source-load model using ZIP (constant impedance (Z), constant current (I), and constant power (P)) as a common load model illustrates how the LVS basics can be articulated. Note that the ZIP load modeling technique takes into account the time-variant and thermal responses of the load model to the voltage alternation, making it a more accurate load modeling technique for CVR.
The power flow equations, including the injected active and reactive powers delivered from the source to the load terminal as the function of the voltage, can be expressed as follows. 
P L = P 0 ( α 1 , P ( v v 0 ) 2 + α 2 , P ( v v 0 ) ) +   α 3 , P
Q L = Q 0 ( α 1 , q ( v v 0 ) 2 + α 2 , q ( v v 0 ) ) +   α 3 , q )
where P and Q are the active and reactive power demands, respectively. In addition, P 0 and Q 0 are the rated active and reactive power at the nominal voltage of V 0 respectively. α1,P (α1,q), α2,P (α2,q) and α3,P (α3,q) are the constant impedance, constant current, and constant power coefficients of the active and reactive power demand, respectively. Accordingly, the relationship between instantaneous active power versus operating voltage for a sample ZIP load model can be driven as in Figure 1. Note that the same methodology can be driven for reactive power as well.
/media/item_content/202303/641a4e50102a0energies-16-02502-g001.png
Figure 1. Power dependency on supply voltage for a 1 kW load using ZIP model [14].
Based on LVS, the voltage sensitivity level varies according to different types of modern power networks as a result of several factors, including the grid’s configuration, load modeling, and the inductance to resistance (X/R) ratio. As illustrated in Figure 1, different load types exhibit diverse responses to CVR since LVS varies in terms of voltage dependency. CVR applications and impacts heavily rely on the different types of loads connected to the power network, and as a result, load modeling is crucial for CVR development. In light of this, a variety of load-modeling strategies are suggested in the literature, introducing various methodologies [15]. 

2.2. CVR Applications in Modern PE-Based Grids

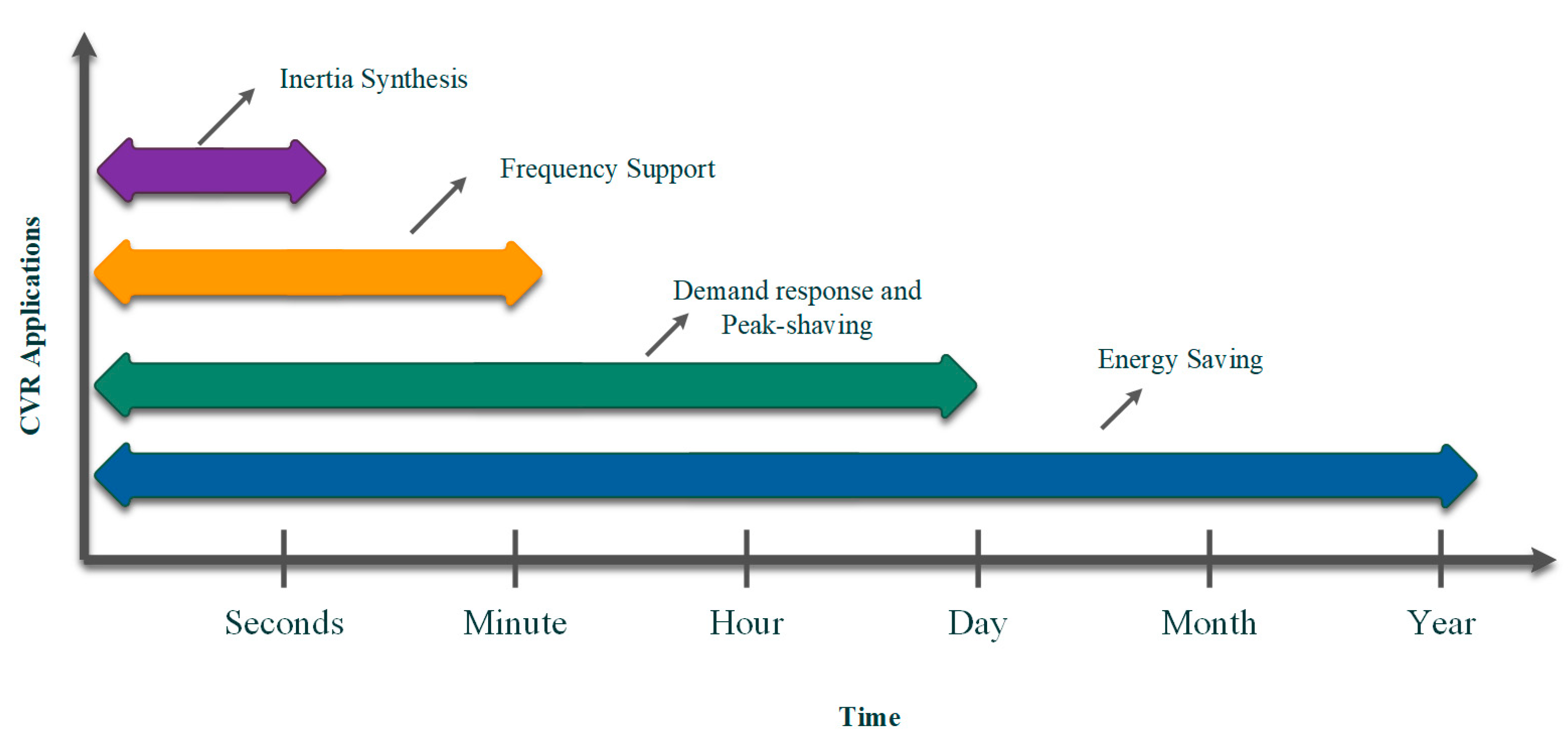
In PE-based grids, CVR is adopted to address both stability and economic issues with a variety of applications over a range of time scales. Categorizing the CVR applications through their time scales provides a new perspective of distinguishing the CVR impact on PE-based grids that leads to using the appropriate CVR implementation techniques, as well as selecting the proper method to quantify and maximize its impacts. An overview of the CVR applications in modern power systems spanning various timescales is shown in Figure 2.
/media/item_content/202303/641a4e643e201energies-16-02502-g002.png
Figure 2. CVR applications in modern PE-based grids at different time scales.

2.2.1. Demand Response, Peak-Shaving, and Energy-Saving via CVR

Reducing desired active/reactive power consumption to save energy is a straightforward CVR use in electric grids. Although the grid configuration and load model have a huge impact on the energy-conserving level, on average, each 1 percent voltage decrease by the CVR is equal to 0.8 percent in the demand power reduction [16]. As the constant power demand types retain the primary load power while utilizing the CVR and lowering the voltage level, it adversely influences these types of demand, such as the PC desktop, TV, PC monitor, and lighting. As a result, by decreasing the voltage, the current rises, increasing power consumption. From a different perspective, the energy consumption level in closed-loop load models, such as the induction stove, increases by lowering the voltage level, and therefore, by using the CVR, the current increases, leading to an increase in the energy consumption level.
In comparison with energy-saving, the CVR application on demand response and peak-shaving happen during a shorter timescale, whereas the employment methodologies are almost the same. To implement the CVR as an energy-saving and peak demand reduction approach in modern grids, DG sitting and sizing processes by considering limits on the voltage span region can be used to effectively reduce the energy consumption level [17][18][19][20][21][22][23][24]. The integration of DG and BESS placement with CVR indicates significant power reduction and increased energy savings, enhancing the system’s functionality and efficiency in the event of a load increase [25]. 

2.2.2. Inertia Synthesis and Dynamics Frequency Support via CVR

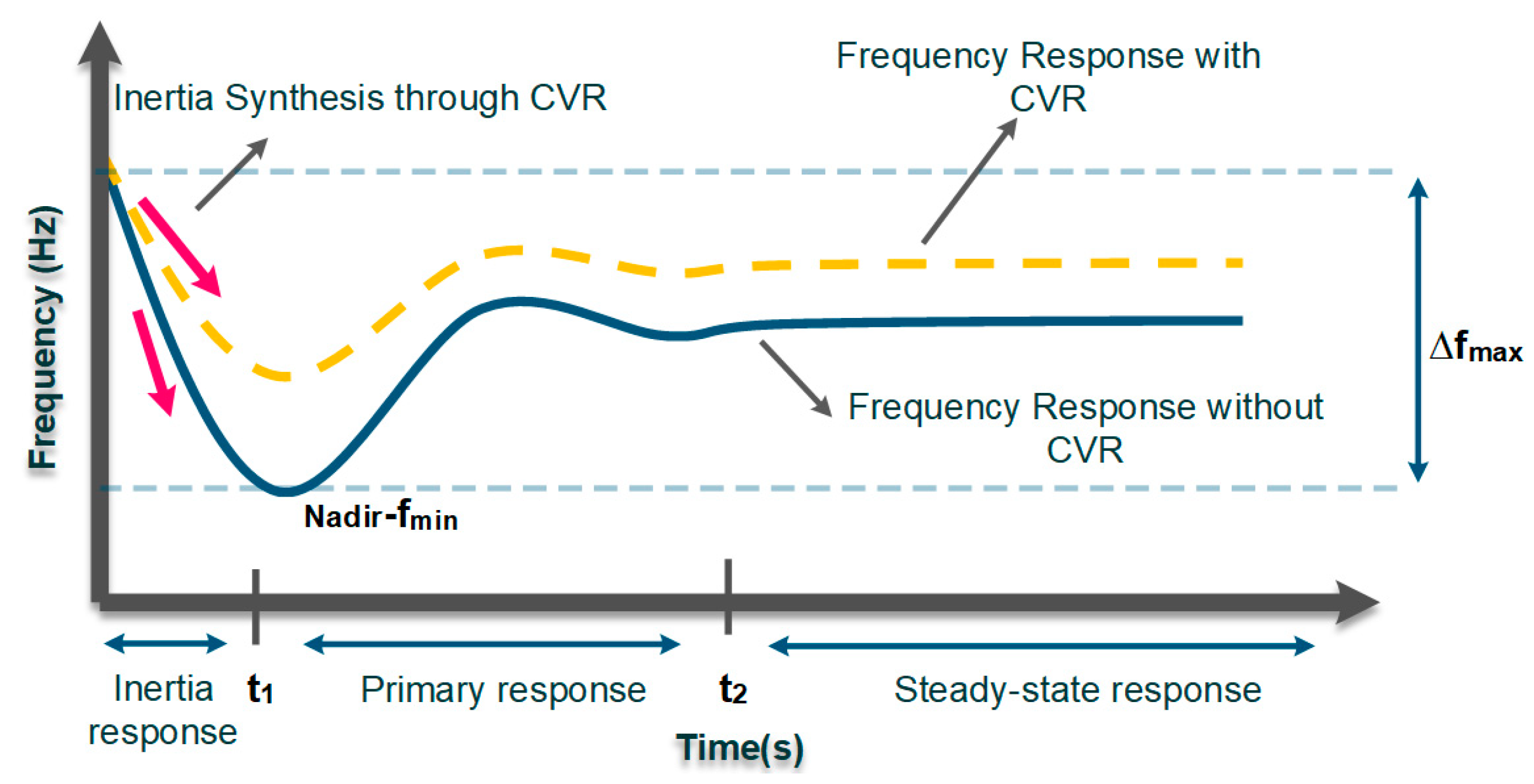
IIDGs owe their connectivity to the emerging advancements in power-electronics technologies, which raise control and stability challenges. MG concepts have been created in the context of smart grids to address control and management issues associated with the high penetration of RESs. However, due to the absence of rotatory mass in PE-based networks, the lack of inertia is a major problem that causes crucial transient and dynamic instabilities as well as excessive frequency fluctuations [26]. Inertia is essential for stabilizing the power system and also smoothing the transient and dynamic response of the power grids. Thus, insufficient inertia in PE-based grids directly impacts the frequency nadir (fmin) and the rate of change of frequency (RoCoF), which is defined as follows:
R o C o F = d f d t ≈ 1 I n e r t i a ∝ 1 H
where H is the inertia constant. It is important to note that pole slipping events that result in critical dynamic instabilities can be caused by RoCoF ranges between 1.5 Hz and 2 Hz [27]. In order to address the aforementioned issues, inertia synthesis and frequency support via CVR is a practical solution aimed at enhancing transient and dynamic stability in PE-based grids (see Figure 3). As the yellow dashed line illustrates by regulating the demand side voltage level and subsequently the demanded active/reactive power, CVR can boost the inertia level by maintaining an instant balance in power generation and consumption. 
/media/item_content/202303/641a4ea8e7225energies-16-02502-g003.png
Figure 3. Inertia synthesis and frequency support via CVR.

3. CVR Implementation Techniques in Modern Grids

3.1. CVR Implementation in PE-Based Grids (Grid-Connected MGs)

Smart inverters and SLs are used to execute CVR in modern grids and grid-connected inverter-dominated MGs. These techniques, which are novel VVO-based solutions, are intended to implement CVR in massive PE-based power systems that also take into account the influence of RESs and IIDGs [28].

3.1.1. CVR through Smart Inverters

The smart inverter is a breakthrough technology for integrating DERs, specifically PVs and WTs, as well as BESSs, into modern grids with operational abilities beyond the inverters’ core functions [29][30].
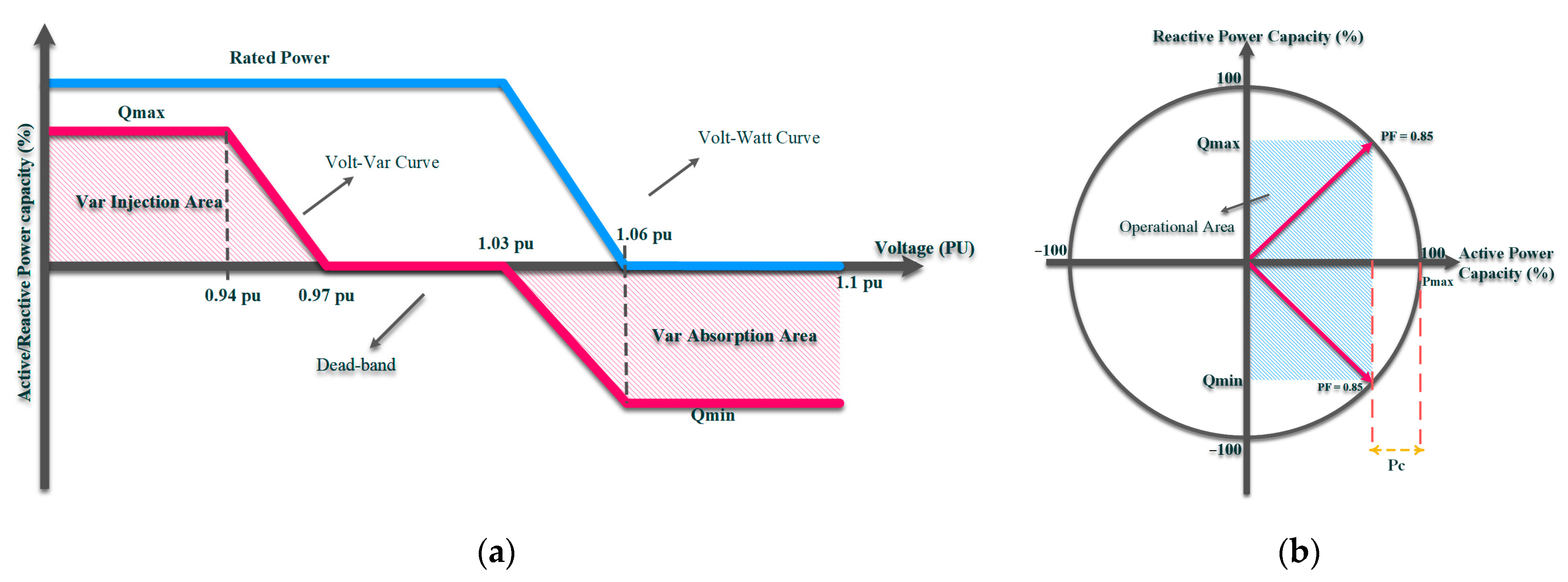
Precisely, with the previous consent of the grid operator, IIDGs were permitted to control voltage under the IEEE Standard 1547 by injecting or absorbing reactive power [31]. Thus, IIDGs can be used as controllable active and/or reactive power sources, and smart inverters can realize their voltage regulation capability. Specifically, the utilities typically restrict the penetration of large-scale PVs and WTs due to their negative effects, such as voltage rise in the distribution network. As a result, smart inverters’ primary application is to solve this problem by regulating the IIDG’s active/reactive power injection or absorption. Depending on the grid configuration, smart inverters may be used to modify the required active/reactive powers of residential-scale loads [32]. Precisely, the smart inverter follows the volt–var curve defined by the utility in the inductive network with a high X/R ratio, see Figure 4.
/media/item_content/202303/641a4ec6c887cenergies-16-02502-g005.png
Figure 4. Smart inverter’s characteristics: (a) smart inverter’s volt–var and volt-watt curves; (b) smart inverter’s operational area.
Hence, based on IIDG’s reactive power injection capacity, the VAr injection occurs in case of voltage drops (less than 0.97 pu) and VAr absorption occurs during the voltage rise (over 1.03 pu). On the other side, the smart inverter follows the defined volt-watt curve in the resistive network with a low X/R ratio and the IIDG’s rated active power mitigates during the voltage rise (over 1.03 pu). Note that costume volt–var and volt-watt curves are defined by the utilities for multiple purposes such as the CVR. The autonomous control mode of smart inverters tracks the volt–var and volt-watt curves for voltage regulation [33].
Smart inverters can also be controlled by designing control rules through data-driven and machine-learning-based methods. Due to higher accuracy and precision when dealing with uncertain grids, machine learning and deep learning techniques have recently attracted a lot of interest [34][35][36][37][38]. Smart inverter-based CVR utilization requires high bandwidth communication links (HBWCL). These communication links are responsible for transmitting data such as referenced active/reactive power and voltage values as well as security signals between utility operators, smart inverters, and measuring equipment. Employing data-driven methods can significantly reduce the use of communication links. 

3.1.2. CVR through Smart Loads

SLs are PE-based equipment can be used to implement CVR by using voltage regulation capabilities to provide inertia synthesis and frequency support [39][40]. Modern PE-based grids use the voltage management capabilities of SLs to modify the required power consumption of large-scale loads to improve the grid’s transient and dynamic responses through CVR.
Electrical loads can be divided into critical (sensitive) and non-critical (NC) types, with the critical loads being unable to withstand a wide range of voltage alternations due to their requirement for uninterrupted, high-quality electricity. In contrast, power consumption in MGs supplying NC loads can be controlled by altering voltage with little to no effect on the consumer. SL is a voltage-dependent NC load connected to a voltage compensator (PE converter with a DC link) that can be employed to inject voltage with controlled magnitude and/or phase angle [41]. Specifically, the combination of voltage-dependent loads coupled with modern equipment, such as PE interfaced converters or electrical springs (ES), forms an SL compact that gives the capability of controlling load power consumption through CVR [42]. Note that an ES passes the RES’s fluctuations to NC loads by allowing their power consumption to vary [43].

3.2. CVR Implementation in Islanded PE-Based MGs

CVR implementation in small-scale islanded MGs is realized through droop controllers [44]. To regulate voltage and frequency and manage the active/reactive power-sharing process among IIDGs, various types of droop schemes, including the conventional, modified, and adaptive types, are used in PE-based MGs [45]. Advanced voltage [46][47][48] and power control [49][50][51] methods are utilized in islanded PE-based MGs to develop droop-based CVR to enhance dynamic stability using frequency support techniques.

4. Quantifying CVR Impacts on Modern Grids

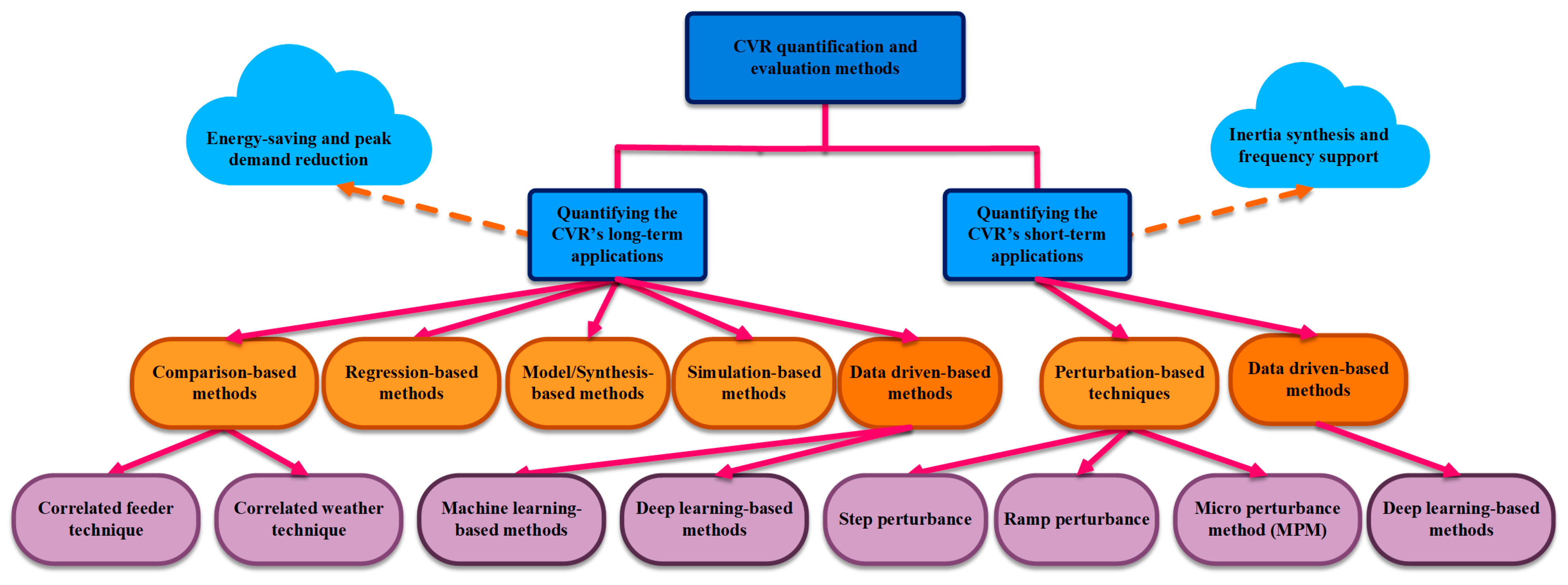
CVR applications in PE-based modern grids should be quantified to represent and evaluate the CVR impacts on voltage, frequency, and demanded active/reactive power. In addition, proposing a benchmark for comparing CVR impacts, enhances the system’s accuracy in selecting the target feeder to maximize voltage reduction amount and consequently maximize the CVR benefits. Classifying the CVR quantification methods based on the CVR application can intensely improve the evaluation methods in terms of finding the proper method, tools, and equipment. Thereby, the overall perspective of the application-based classification of CVR quantification techniques is depicted in Figure 5.
/media/item_content/202303/641a4ee83b7d0energies-16-02502-g013.png
Figure 5. The overall perspective of CVR quantification methods.

4.1. Quantifying the CVR’s Long-Term Applications

CVR factor is commonly used to quantify the long-term CVR applications and can be expressed for active/reactive power as follows [52]:
CVR f ,   P = % Δ P % Δ V = % ( P post − P pre P mean ) × 100 % ( V post − V pre ) / V mean × 100
CVR f ,   Q = % Δ Q % Δ V = % ( Q post − Q pre Q mean ) × 100 % ( V post − V pre ) / V mean × 100
where V post ( V pre ), P post ( P pre ), and Q post ( Q pre ) are the measured values of voltage, active and reactive powers, after (before) CVR adjustment, respectively. In addition, V mean , P mean , and Q mean are the mean values of voltage, active, and reactive powers, respectively.
Several CVR-factor derivation techniques concentrate on steady-state time scales that quantify the CVR’s long-term applications, such as energy saving. The following categories apply to these techniques.
  • comparison-based methods;
  • regression-based methods;
  • model/synthesis-based methods;
  • simulation-based methods;
  • data-driven-based methods.

4.2. Quantifying the CVR’s Short-Term Applications

As transients/dynamic stability in modern grids is improved through short-term applications of the CVR (i.e., inertia synthesis and frequency support), quantifying CVR impacts during mentioned time scales is not possible by using traditional quantification techniques with the high penetration of IIDGs. Critical issues and challenges of applying conventional techniques for evaluating CVR short-term applications are listed as follows:
  • A critical issue is with the natural fluctuations of the inverter-interfaced suppliers’ impact in PE-based grids on voltage profile, which distorts the CVR effects. The fast response of the PE-based suppliers and consumers (i.e., IIDGs, and SLs) needs real-time quantification methods. However, the traditional quantification methods are unable to track the CVR impact continuously and in real-time.
  • Further, since all of the traditional quantification techniques outlined in the preceding sections are focused on steady states, they are unable to quantify and follow the effect of CVR on transients and dynamics. Alternative techniques are therefore required to fully quantify and assess the CVR across all time scales.
  • Moreover, distinguishing between the load’s change behavior and the data noise during the transients and dynamics becomes bold. In light of this, a suitable noise reduction methodology, not covered by the other methods, is urgently required for estimating CVR in modern PE-based grids.
Thereby, alternative quantification methods are proposed aiming to address the aforementioned difficulties and problems.

4.2.1. Perturbation-Based Techniques

Perturbation-based approaches are online CVR evaluation frameworks that measure CVR-related load and voltage data in real time to evaluate CVR effects [53][54][55][56][57]. Thus, for quantifying the needed data in a continuous manner, proactive voltage perturbation schemes are employed. The perturbation induces the CVR effect; meanwhile, the CVR factor is continuously calculated through experimental data. Note that various perturbation-based quantification approaches utilize various perturbation signals, noise reduction strategies, and CVR quantification indices.

4.2.2. Data-Driven Based Techniques (Short-Term Applications)

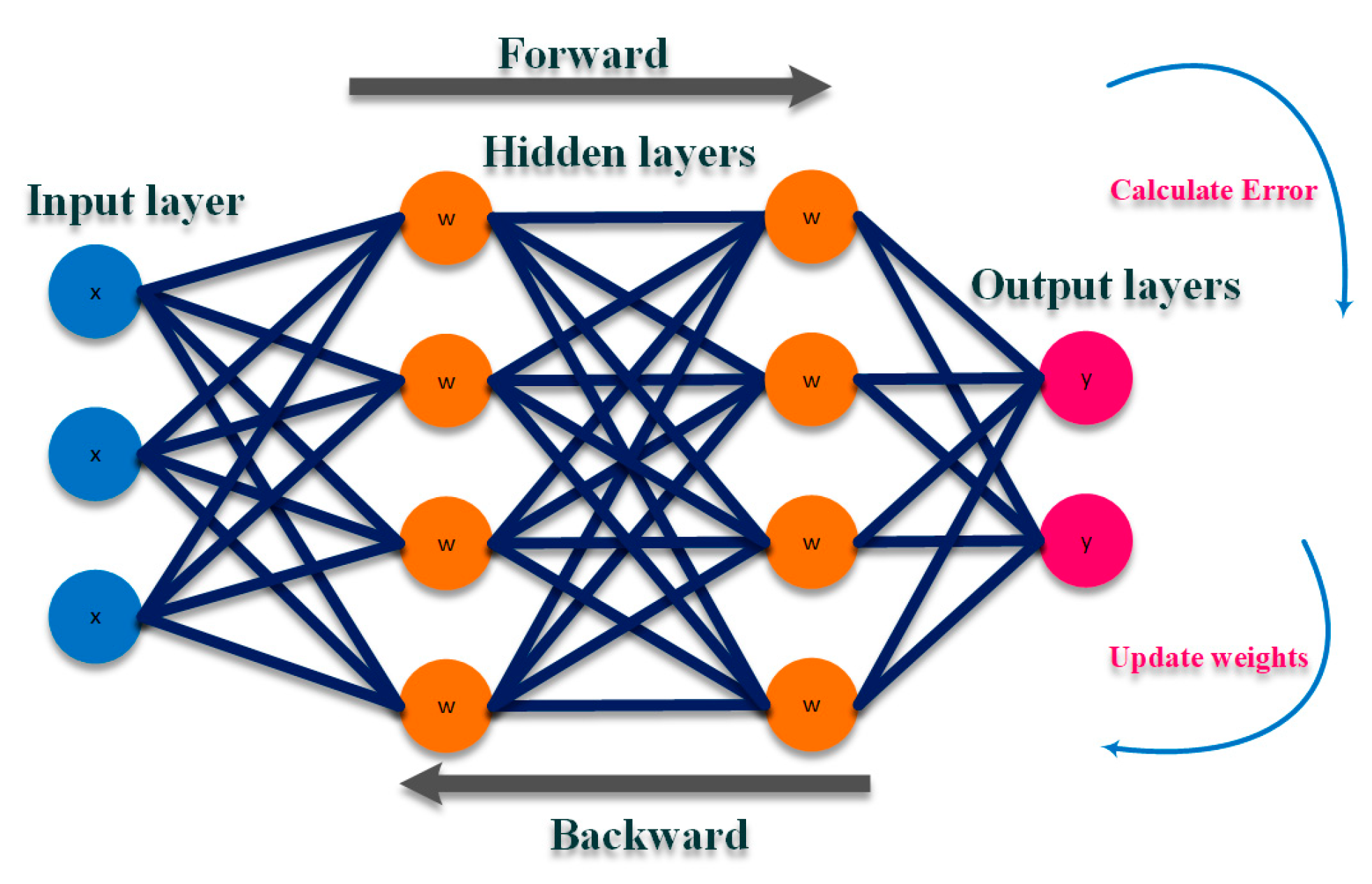
Data-driven methods in quantifying the short-term CVR applications are focused on DNN-based algorithms that show high accuracy in evaluating the CVR impacts [58][59]. In light of this, a DNN model with a backpropagation training algorithm is proposed in [58] to analyze the behavior of the CVR and its effects on the target feeder. As shown in Figure 6, in a backpropagation-based DNN algorithm the DNN forwards the received inputs and associates them with weights and biases to produce the output. Then, in an iterative scheme, the DNN is trained with a supervised learning approach, in which the difference between the system’s output and a known predicted output as an error is supplied to the training algorithm. Thereby, the weights are updated to minimize the global error driven in each iteration according to the updated weights in a forward and backward algorithm.
/media/item_content/202303/641a4fe978743energies-16-02502-g021.png
Figure 6. Sample DNN with a backpropagation algorithm.
In the proposed DNN-based quantification technique the model is trained through the Levenberg–Marquardt training method which considers day, hour, and whether information as the load profile inputs. The proposed model predicts load savings and creates a CVR baseline. Unlike the similarity-based techniques, the DNN acts as a generative-based scheme to estimate the output load saving. Thereby, the method accuracy is highly increased, making the proposed model a precise quantification technique. In this scheme, the dynamic load behavior can be tracked by the proposed technique which makes the model capable of evaluating the short-term applications of the CVR. The practical result on multiple substations in Washington EMC utility shows high accuracy with 0.22% error in tracking and generating the load during the dynamics change load behavior by the CVR.

References

  1. Moradi, M.H.; Eskandari, M.; Hosseinian, S.M. Cooperative Control Strategy of Energy Storage Systems and Micro Sources for Stabilizing Microgrids in Different Operation Modes. Int. J. Electr. Power Energy Syst. 2016, 78, 390–400.
  2. Eskandari, M.; Rajabi, A.; Rezaeimozafar, M.; Savkin, A.V.; Member, S.; Moradi, M.H.; Dong, Z.Y. Battery Energy Storage Systems (BESSs) and the Economy- Dynamics of Microgrids: Review, Analysis, and Classification for Standardization of BESSs Applications. J. Energy Storage 2022, 55, 105627.
  3. Ma, Z.; Xiang, Y.; Wang, Z. Robust Conservation Voltage Reduction Evaluation Using Soft Constrained Gradient Analysis. IEEE Trans. Power Syst. 2022, 37, 4485–4496.
  4. McNamara, M.; Fengand, D.; Pettit, T.; Lawlor, D. Conservation Voltage Reduction/Volt VAR Optimization EM&V Practices. 2017. Available online: https://www.energystar.gov/ (accessed on 19 January 2017).
  5. Ranamuka, D.; Agalgaonkar, A.P.; Muttaqi, K.M. Conservation Voltage Reduction and VAr Management Considering Urban Distribution System Operation with Solar-PV. Int. J. Electr. Power Energy Syst. 2019, 105, 856–866.
  6. Moradi, M.H.; Eskandari, M.; Mahdi Hosseinian, S. Operational Strategy Optimization in an Optimal Sized Smart Microgrid. IEEE Trans. Smart Grid 2015, 6, 1087–1095.
  7. Hirsch, A.; Parag, Y.; Guerrero, J. Microgrids: A Review of Technologies, Key Drivers, and Outstanding Issues. Renew. Sustain. Energy Rev. 2018, 90, 402–411.
  8. Dheer, D.K.; Soni, N.; Doolla, S. Improvement of Small Signal Stability Margin and Transient Response in Inverter-Dominated Microgrids. Sustain. Energy Grids Netw. 2016, 5, 135–147.
  9. Worighi, I.; Maach, A.; Hafid, A.; Hegazy, O.; van Mierlo, J. Integrating Renewable Energy in Smart Grid System: Architecture, Virtualization and Analysis. Sustain. Energy Grids Netw. 2019, 18, 100226.
  10. Asadi, Y.; Eskandari, M.; Mansouri, M.; Savkin, A.V.; Pathan, E. Frequency and Voltage Control Techniques through Inverter-Interfaced Distributed Energy Resources in Microgrids: A Review. Energies 2022, 15, 8580.
  11. Mehrkhodavandi, H.; Arefi, A.; Yazdani, A.; Najmizadeh, A.; Fani, S. Virtual Inertia a Must for Mitigation of Frequency Instability in Microgrids: A Comprehensive Review. In Proceedings of the 2021 31st Australasian Universities Power Engineering Conference, AUPEC 2021, Perth, Australia, 26–30 September 2021.
  12. Farrokhabadi, M.; Cañizares, C.A.; Bhattacharya, K. Frequency Control in Isolated/Islanded Microgrids through Voltage Regulation. IEEE Trans. Smart Grid 2017, 8, 1185–1194.
  13. Schneider, K.P.; Radhakrishnan, N.; Tang, Y.; Tuffner, F.K.; Liu, C.C.; Xie, J.; Ton, D. Improving Primary Frequency Response to Support Networked Microgrid Operations. IEEE Trans. Power Syst. 2019, 34, 659–667.
  14. McKenna, K.; Keane, A. Open and Closed-Loop Residential Load Models for Assessment of Conservation Voltage Reduction. IEEE Trans. Power Syst. 2017, 32, 2995–3005.
  15. Zhao, J.; Wang, Z.; Wang, J. Robust Time-Varying Load Modeling for Conservation Voltage Reduction Assessment. IEEE Trans. Smart Grid 2018, 9, 3304–3312.
  16. Pinney, D. Costs and Benefits of Conservation Voltage Reduction; National Rural Cooperative Association: Arlington, VA, USA, 2013.
  17. Wang, Z.; Chen, B.; Wang, J.; Begovic, M.M. Stochastic DG Placement for Conservation Voltage Reduction Based on Multiple Replications Procedure. IEEE Trans. Power Deliv. 2015, 30, 1039–1047.
  18. Haidar, Z.; Waqar, A.; Adamali Shah, N.M.; Al-Mutib, K. Optimal Power Flow Using Distributed Generation and Conservation Voltage Reduction Techniques for Micro-Grids. In Proceedings of the 2018 International Conference on Emerging Trends and Innovations in Engineering And Technological Research, ICETIETR 2018, Ernakulam, India, 11–13 July 2018.
  19. Pamshetti, V.B.; Thakur, A.K.; Singh, S.; Singh, S.P. Bi-Level Operational Planning of Microgrids Considering Conservation Voltage Reduction. In Proceedings of the 9th IEEE International Conference on Power Electronics, Drives and Energy Systems, PEDES 2020, Jaipur, India, 16–19 December 2020.
  20. Hossan, M.S.; Chowdhury, B.; Arora, M.; Lim, C. Effective CVR Planning with Smart DGs Using MINLP. In Proceedings of the 2017 North American Power Symposium, NAPS 2017, Morgantown, WV, USA, 17–19 September 2017.
  21. Gheydi, M.; Nouri, A.; Ghadimi, N. Planning in Microgrids with Conservation of Voltage Reduction. IEEE Syst. J. 2018, 12, 2782–2790.
  22. Quijano, D.A.; Padilha-Feltrin, A. Optimal Integration of Distributed Generation and Conservation Voltage Reduction in Active Distribution Networks. Int. J. Electr. Power Energy Syst. 2019, 113, 197–207.
  23. Moradi, M.H.; Eskandari, M.; Showkati, H. A Hybrid Method for Simultaneous Optimization of DG Capacity and Operational Strategy in Microgrids Utilizing Renewable Energy Resources. Int. J. Electr. Power Energy Syst. 2014, 56, 241–258.
  24. Soykan, G.; Er, G.; Canakoglu, E. Optimal Sizing of an Isolated Microgrid with Electric Vehicles Using Stochastic Programming. Sustain. Energy Grids Netw. 2022, 32, 100850.
  25. Zhang, Y.; Ren, S.; Dong, Z.Y.; Xu, Y.; Meng, K.; Zheng, Y. Optimal Placement of Battery Energy Storage in Distribution Networks Considering Conservation Voltage Reduction and Stochastic Load Composition. IET Gener. Transm. Distrib. 2017, 11, 3862–3870.
  26. Azizi, S.; Sun, M.; Liu, G.; Terzija, V. Local Frequency-Based Estimation of the Rate of Change of Frequency of the Center of Inertia. IEEE Trans. Power Syst. 2020, 35, 4948–4951.
  27. DNV KEMA Energy & Sustainability; EirGrid RoCoF an Independent Analysis on the Ability of Generators to Ride through Rate of Change of Frequency Values up to 2 Hz/s. Available online: http://www.eirgridgroup.com/site-files/library/EirGrid/DNV-KEMA_Report_RoCoF_20130208final_pdf (accessed on 12 February 2022).
  28. Padullaparti, H.V.; Nguyen, Q.; Santoso, S. Advances in Volt-Var Control Approaches in Utility Distribution Systems. In Proceedings of the IEEE Power and Energy Society General Meeting 2016, Boston, MA, USA, 17–21 July 2016.
  29. Pecenak, Z.K.; Kleissl, J.; Disfani, V.R. Smart Inverter Impacts on California Distribution Feeders with Increasing Pv Penetration: A Case Study. In Proceedings of the IEEE Power and Energy Society General Meeting 2017, Chicago, IL, USA, 16–20 July 2017; pp. 1–5.
  30. Gargoom, A.; Elmusrati, M.; Gaouda, A. Enhancing the Operation of Smart Inverters with PMU and Data Concentrators. Int. J. Electr. Power Energy Syst. 2022, 140, 108077.
  31. IEEE Standard Association IEEE Std. 1547-2018. Standard for Interconnection and Interoperability of Distributed Energy Resources with Associated Electric Power Systems Interfaces. Available online: https://standards.ieee.org/standard/1547-2018.html (accessed on 26 December 2021).
  32. Sunderman, W.; Dugan, R.C.; Smith, J. Open Source Modeling of Advanced Inverter Functions for Solar Photovoltaic Installations. In Proceedings of the IEEE Power Engineering Society Transmission and Distribution Conference, Chicago, IL, USA, 14–17 April 2014.
  33. Ding, F.; Pratt, A.; Bialek, T.; Bell, F.; McCarty, M.; Atef, K.; Nagarajan, A.; Gotseff, P. Voltage Support Study of Smart PV Inverters on a High-Photovoltaic Penetration Utility Distribution Feeder. In Proceedings of the Conference Record of the IEEE Photovoltaic Specialists Conference 2016, Portland, OR, USA, 5–10 June 2016; pp. 1375–1380.
  34. Hu, J.; Liu, Z.; Chen, J.; Hu, W.; Zhang, Z.; Chen, Z. A Novel Deep Learning–Based Fault Diagnosis Algorithm for Preventing Protection Malfunction. Int. J. Electr. Power Energy Syst. 2023, 144, 108622.
  35. Kanwal, S.; Khan, B.; Muhammad Ali, S. Machine Learning Based Weighted Scheduling Scheme for Active Power Control of Hybrid Microgrid. Int. J. Electr. Power Energy Syst. 2021, 125, 106461.
  36. Li, L.; Zhang, S. Peer-to-Peer Multi-Energy Sharing for Home Microgrids: An Integration of Data-Driven and Model-Driven Approaches. Int. J. Electr. Power Energy Syst. 2021, 133, 107243.
  37. Fellner, D.; Strasser, T.I.; Kastner, W. Applying Deep Learning-Based Concepts for the Detection of Device Misconfigurations in Power Systems. Sustain. Energy Grids Netw. 2022, 32, 100851.
  38. Ozcanli, A.K.; Baysal, M. Islanding Detection in Microgrid Using Deep Learning Based on 1D CNN and CNN-LSTM Networks. Sustain. Energy Grids Netw. 2022, 32, 100839.
  39. Pilehvar, M.S.; Shadmand, M.B.; Mirafzal, B. Analysis of Smart Loads in Nanogrids. IEEE Access 2019, 7, 548–562.
  40. Darbandsari, A.; Amraee, T. Under Frequency Load Shedding for Low Inertia Grids Utilizing Smart Loads. Int. J. Electr. Power Energy Syst. 2022, 135, 107506.
  41. Akhtar, Z.; Chaudhuri, B.; Hui, S.Y.R. Smart Loads for Voltage Control in Distribution Networks. IEEE Trans. Smart Grid 2017, 8, 937–946.
  42. Chen, T.; Guo, J.; Chaudhuri, B.; Hui, S.Y. Virtual Inertia from Smart Loads. IEEE Trans. Smart Grid 2020, 11, 4311–4320.
  43. Pawar, R.S.; Gawande, S.P.; Kadwane, S.G.; Waghmare, M.A.; Nagpure, R.N. Electric Spring Configurations: Comprehensive Analysis. In Proceedings of the 2018 IEEE International Conference on Power, Instrumentation, Control and Computing, PICC 2018, Thrissur, India, 18–20 January 2018; pp. 1–6.
  44. Eskandari, M.; Li, L.; Moradi, M.H.; Siano, P.; Blaabjerg, F. Active Power Sharing and Frequency Restoration in an Autonomous Networked Microgrid. IEEE Trans. Power Syst. 2019, 34, 4706–4717.
  45. Eskandari, M.; Li, L.; Moradi, M.H.; Siano, P. A Nodal Approach Based State-Space Model of Droop-Based Autonomous Networked Microgrids. Sustain. Energy Grids Netw. 2019, 18, 100216.
  46. Guo, C.; Wang, X.; Zheng, Y.; Zhang, F. Real-Time Optimal Energy Management of Microgrid with Uncertainties Based on Deep Reinforcement Learning. Energy 2022, 238, 121873.
  47. Jendoubi, I.; Bouffard, F. Data-Driven Sustainable Distributed Energy Resources’ Control Based on Multi-Agent Deep Reinforcement Learning. Sustain. Energy Grids Netw. 2022, 32, 100919.
  48. Eskandari, M.; Savkin, A.V.; Fletcher, J. A Deep Reinforcement Learning-Based Intelligent Grid-Forming Inverter for Inertia Synthesis by Impedance Emulation. IEEE Trans. Power Syst. 2023, 1–4.
  49. Eskandari, M.; Li, L.; Moradi, M.H. Decentralized Optimal Servo Control System for Implementing Instantaneous Reactive Power Sharing in Microgrids. IEEE Trans. Sustain. Energy 2018, 9, 525–537.
  50. Eskandari, M.; Li, L.; Moradi, M.H.; Siano, P.; Blaabjerg, F. Simultaneous Reactive Power Sharing and Voltage Regulation in an Autonomous Networked Microgrid. IET Gener. Transm. Distrib. 2020, 14, 1366–1377.
  51. Eskandari, M.; Li, L.; Moradi, M.H.; Wang, F.; Blaabjerg, F. A Control System for Stable Operation of Autonomous Networked Microgrids. IEEE Trans. Power Deliv. 2020, 35, 1633–1647.
  52. Shim, K.S.; Go, S.I.; Yun, S.Y.; Choi, J.H.; Nam-Koong, W.; Shin, C.H.; Ahn, S.J. Estimation of Conservation Voltage Reduction Factors Using Measurement Data of KEPCO System. Energies 2017, 10, 2148.
  53. de Carne, G.; Bruno, S.; Liserre, M.; la Scala, M. Distributed Online Load Sensitivity Identification by Smart Transformer and Industrial Metering. IEEE Trans. Ind. Appl. 2019, 55, 7328–7337.
  54. Jayaraman, S.; Miranbeigi, M.; Kandula, R.P.; Divan, D. Improving Energy Efficiency and Productivity at Industrial Plants Using Dynamic Voltage Management. IEEE Trans. Ind. Appl. 2020, 56, 1250–1257.
  55. Xu, J.; Xie, B.; Liao, S.; Ke, D.; Sun, Y.; Jiang, X.; Yu, J. CVR-Based Real-Time Power Fluctuation Smoothing Control for Distribution Systems with High Penetration of PV and Experimental Demonstration. IEEE Trans. Smart Grid 2022, 13, 3619–3635.
  56. Jayaraman, S.; Miranbeigi, M.; Kandula, P.; Grant, T.; Divan, D. Reducing Energy Consumption in Industrial Plants Using behind the Meter Conservation Voltage Reduction. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition, ECCE 2018, Portland, OR, USA, 23–27 September 2018; pp. 4791–4798.
  57. Xu, J.; Xie, B.; Liao, S.; Sun, Y.; Ke, D.; Yang, J.; Li, P.; Yu, L.; Xu, Q.; Ma, X. Online Assessment of Conservation Voltage Reduction Effects with Micro-Perturbation. IEEE Trans. Smart Grid 2021, 12, 2224–2238.
  58. El-Shahat, A.; Haddad, R.J.; Alba-Flores, R.; Rios, F.; Helton, Z. Conservation Voltage Reduction Case Study. IEEE Access 2020, 8, 55383–55397.
  59. Yadav, G.; Liao, Y.; Jewell, N.; Ionel, D.M. CVR Study and Active Power Loss Estimation Based on Analytical and ANN Method. Energies 2022, 15, 4689.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Engineering, Electrical & Electronic
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Alireza Gorjian
,
Mohsen Eskandari
,
Mohammad H. Moradi
View Times: 426
Revisions: 2 times (View History)
Update Date: 22 Mar 2023
Table of Contents
    1000/1000
    Hot Most Recent
    Video Production Service
    Feedback