Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Xuelong Yang
 -- 3015 2023-02-03 09:52:49 |
2 update references and layout
Rita Xu
 Meta information modification 3015 2023-02-03 10:00:50 |

Video Upload Options

We provide professional Video Production Services to translate complex research into visually appealing presentations. Would you like to try it?
No, upload directly Yes

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Zhang, H.;  Zou, D.;  Yang, X.;  Mou, J.;  Zhou, Q.;  Xu, M. Liquid–Gas Jet Pump. Encyclopedia. Available online: https://encyclopedia.pub/entry/40803 (accessed on 28 December 2024).
Zhang H,  Zou D,  Yang X,  Mou J,  Zhou Q,  Xu M. Liquid–Gas Jet Pump. Encyclopedia. Available at: https://encyclopedia.pub/entry/40803. Accessed December 28, 2024.
Zhang, Huiyan, Daohang Zou, Xuelong Yang, Jiegang Mou, Qiwei Zhou, Maosen Xu. "Liquid–Gas Jet Pump" Encyclopedia, https://encyclopedia.pub/entry/40803 (accessed December 28, 2024).
Zhang, H.,  Zou, D.,  Yang, X.,  Mou, J.,  Zhou, Q., & Xu, M. (2023, February 03). Liquid–Gas Jet Pump. In Encyclopedia. https://encyclopedia.pub/entry/40803
Zhang, Huiyan, et al. "Liquid–Gas Jet Pump." Encyclopedia. Web. 03 February, 2023.
Liquid–Gas Jet Pump
Edit
This entry is adapted from the peer-reviewed paper 10.3390/en15196978

The liquid–gas jet pump (LGJP) is a kind of fluid conveying machinery and mixing reaction equipment, utilizing high-speed working liquid ejected from the nozzle to transfer energy to pumped gas through momentum exchange.

liquid–gas jet pump pulsed liquid–gas jet pump centrifugal jet vacuum pump gas–liquid two-phase flow

1. Introduction

The liquid–gas jet pump (LGJP) has the advantages of a simple structure, easy processing, simple installation, good sealing, no moving parts and easy maintenance and is widely used, especially under various special working conditions such as high temperature, high pressure, vacuum and underwater [1][2][3][4][5][6]. However, the low energy transfer efficiency of the LGJP is not conducive to its further promotion and use. Therefore, a current focus of research is on how to keep the LGJP running efficiently under different applications [7][8]. At the same time, a change in operating conditions will also affect the performance of the LGJP, so improving its adaptability to operating conditions has also attracted more attention from scholars [9][10][11]. Scholars have carried out a lot of work on the LGJP using theoretical analysis, experimental research and computational fluid dynamics (CFD) technology to explore its internal two-phase flow and gas suction mechanism in an attempt to fundamentally solve these problems [12][13][14][15].

2. Structure and Principle

The LGJP is mainly composed of four parts: the nozzle, the mixing chamber, the throat and the diffuser (see Figure 1). When the working fluid (liquid) is spewed out at high speed from the nozzle, the gas around it is sucked to form negative pressure in the mixing chamber, and the suction gas is sucked in. The two fluids are then mixed in the throat and exchange momentum, so that the velocity of the working fluid decreases and the velocity of the sucked gas increases. At the outlet of the throat, the velocities of the two fluids are basically the same. The velocity of the mixed fluid in the diffuser gradually decreases while the pressure gradually increases, converting kinetic energy into pressure energy.
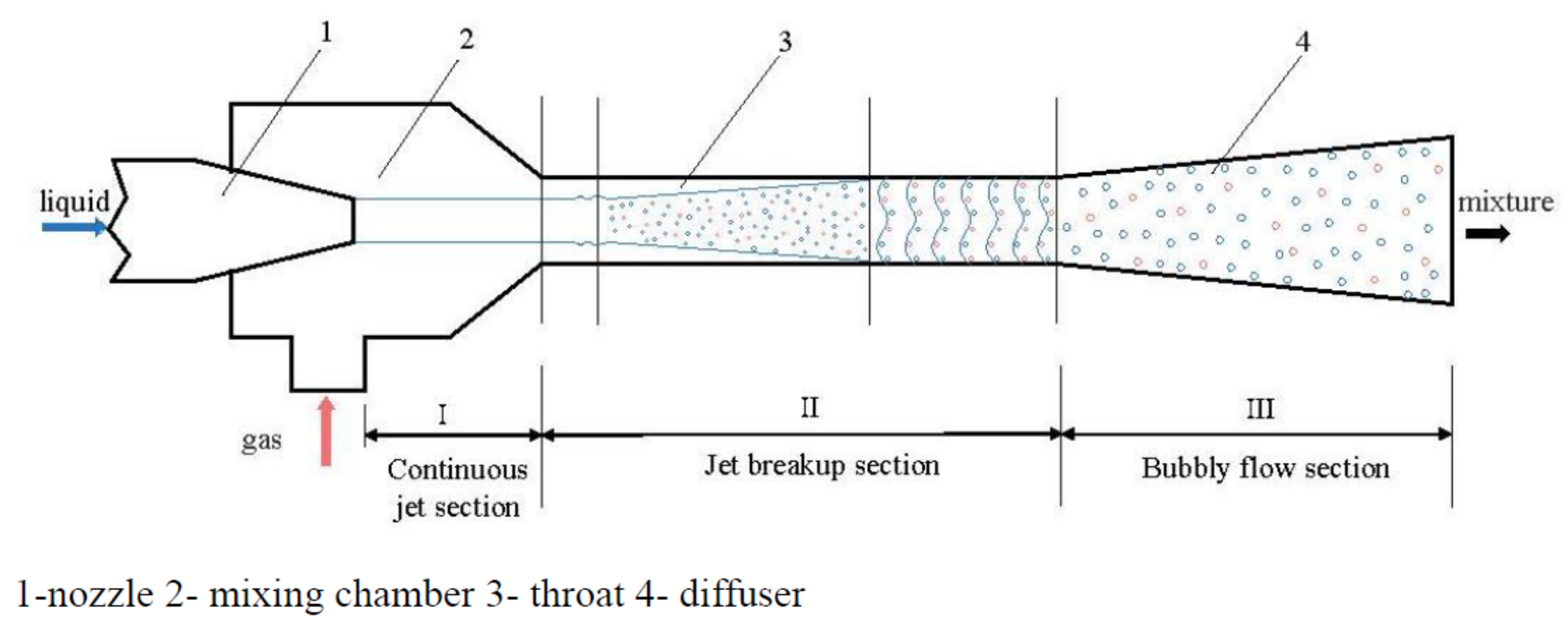
Energies 15 06978 g001
Figure 1. Working principle and structure diagram of the LGJP.
The liquid and gas in the mixing chamber have different velocities, and when the two are mixed, a large energy loss occurs, which reduces the efficiency of the LGJP. At present, the methods to improve the mixing efficiency mainly include structural optimization [2][4][5][6] and the use of pulsed jets [16], that is, a pulsed liquid–gas jet pump (PLGJP). There are two main ways of pulse generation: one is to install the pulse generator at the front of the nozzle without changing the original liquid–gas jet pump structure, so that the working liquid has a certain pulse frequency [15]; the other is the centrifugal jet vacuum pump [6] (CJVP).
The CJVP adopts the structure of the runner nozzle and the deflector on the basis of retaining the LGJP mixing chamber, throat, diffuser and other structures (see Figure 2). Only when the runner nozzle communicates with the deflector and the mixing chamber can the working fluid be thrown out into the mixing chamber through the runner nozzle, and the connection time of each runner nozzle is limited, thereby generating a pulsed jet.
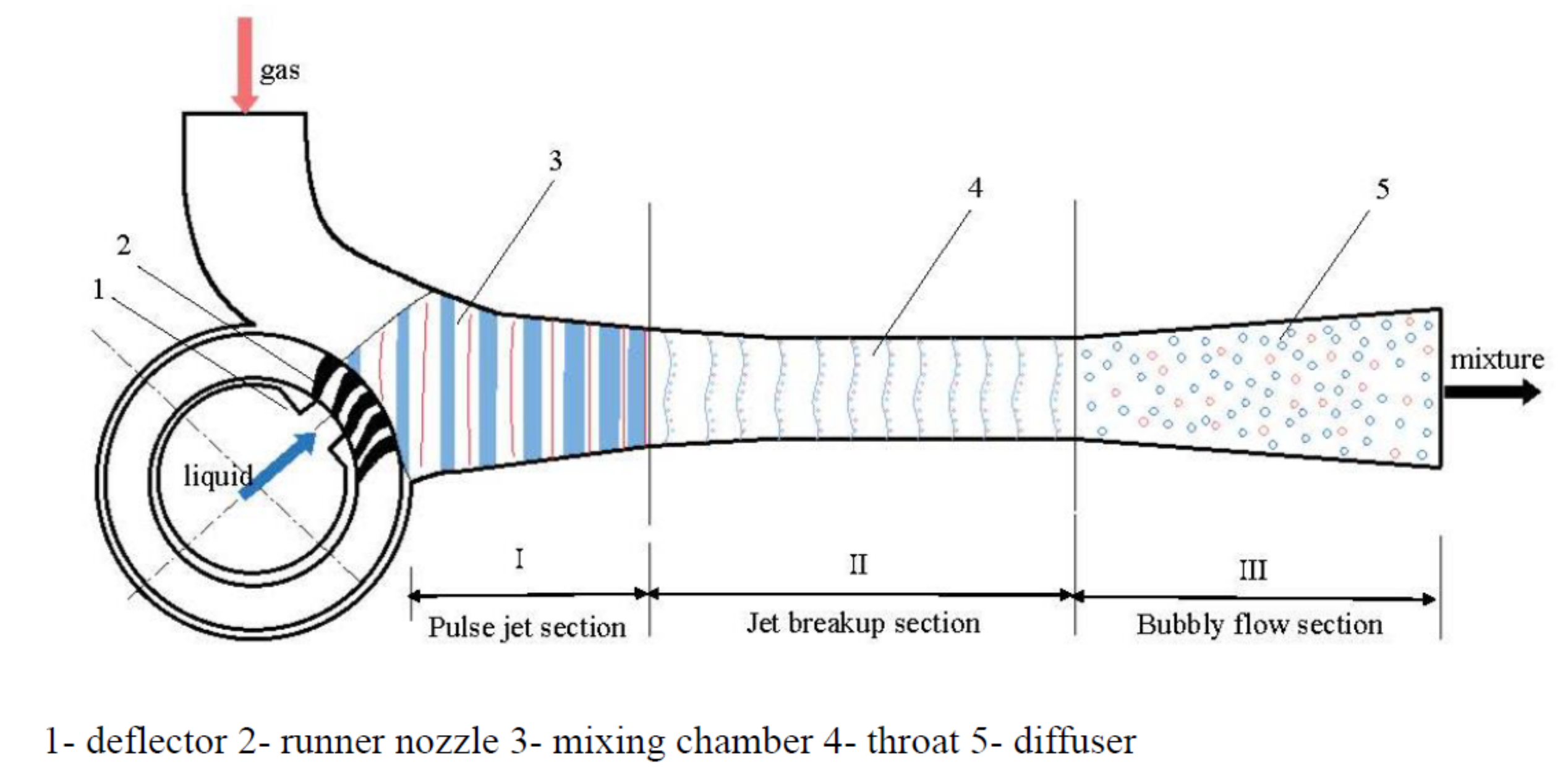
Energies 15 06978 g002
Figure 2. Working principle and structure diagram of the CJVP.
Pulse jets can rapidly mix fluids, thereby reducing the length of the mixing section. The PLGJP has good suction performance because the inertial force of the pulse jet increases the working pressure of the jet pump, thereby improving the suction capacity. There are two ways for the pulsed jet to carry the gas into the suction chamber: one is the viscous effect between the fluids, and the other is that the gap between the pulsed jets ejected from the nozzle plays the role of the piston pump. The pulse frequency generated by a pulse generator is usually less than 10 Hz [6], while the pulse frequency generated by a CJVP can reach more than 1000 Hz, so it has higher suction capacity and efficiency.

3. Research Status of the LGJP

Jet pump design theory has been studied for more than 150 years. As early as the 1860s, the German scholar Zeune [17] established the theoretical basis of jet pump design according to the momentum theorem. Although the research of the jet pump has a long history, it was not until the 1930s that, with the continuous development of science and the continuous improvement of the knowledge system about fluid mechanics and aerodynamics, the theoretical research and practical application of the LGJP were further developed. The specific concept of the LGJP was first proposed by the scholar Hoeffer [2] in 1922 and was successfully applied in the vacuum pumping experiment of a condenser. Subsequently, a large number of research papers on the LGJP were published in various magazines. Then, through a large number of experimental studies conducted by Rammingen [18], they discovered the sudden rise in the pressure of the two-phase fluid after mixing at the throat. Then more scholars began to study the effect of changing the length of the throat on the mixing performance of the gas–liquid two-phase flow on this basis to obtain the approximate range of the optimal length. At the same time, Bonnington [3] found in the gas–liquid two-phase mixing experiment of the transparent throat that as the flow rate of the LGJP increased, the entrainment efficiency of the LGJP decreased. The gas effect was obviously improved. Within a certain length of the throat, the longer the throat, the better the entrainment effect.
Witte [17] was the first to combine the application of the Euler equation with the theoretical analysis of the LGJP and described the flow process of the two-phase fluid in the tube in detail, thereby defining the mixed shock wave. He found that the two-phase fluid in the flow mixing process showed a great influence on the compressed gas, and the structure of the LGJP was further optimized. Higgins [4] deduced the unary relationship of the drag coefficient introduced by the LGJP and verified the correctness of the theoretical derivation through experiments. The results showed that the suction performance was the best when the two-phase fluid was mixed at the throat outlet of the LGJP. Lu [5][6] derived the basic performance equation of the LGJP based on the simplified method of unitary flow, optimized some parameters, took into account the influence of different flow rates of each structural plane in the pump and verified the accuracy of the theoretical equation through experiments. On this basis, he comprehensively summarized the research results of experts and scholars at home and abroad on the jet pump. In 1989, he published a monograph on jet technology, the Theory and Application of Liquid–Gas Jet Pump Technology, and in 2004, he published again, the Theory and Application of Jet Technology. Long [7] obtained the performance equation of the LGJP under the condition of constant determination based on the relevant theories of fluid mechanics on the premise of constant determination of the basic performance equation of the LGJP, laying a foundation for further study and analysis of the internal flow mechanism of the unsteady liquid–gas jet pump.
Betzler [5] used experiments to analyze the influence of the size of the diffuser, and the results showed that the LGJP displayed better suction performance when the two-phase fluid was completely mixed before entering the diffuser. When optimizing the overall structure of the LGJP, it was found that when the length–diameter ratio of the throat was 23, the gas isothermal compression rate of the LGJP could reach about 19%. Based on a large number of experimental results, Cunningham [18] analyzed that the gas isothermal compression efficiency of the LGJP could reach 40% or even higher under optimal working conditions as long as the structural parameters of the LGJP, such as the throat length–diameter ratio and throat diameter, were given reasonable values. When Neve [4] tested the performance of the diffuser of the LGJP, he found that the performance of the diffuser was related to the degree of homogeneous mixing of the two-phase fluid in the diffuser and the inconsistency of velocity at the entrance of the diffuser.
Haidl [8] used a converging nozzle to measure the suction capacity of a conventional liquid–gas jet pump while experimenting with the performance of the pump in less stable configurations, providing the best design suggestions for units with various geometric shapes, directions and operating conditions to minimize gas entrainment. Opletal [10] studied the influence of the geometric parameters of the jet pump on the injection ratio and mass transfer coefficient, showed that the working structure parameters had an important influence on the injection performance of the LGJP and proposed a method to evaluate the mass transfer performance. Kim [11] and others simulated and analyzed that the suction rate of a LGJP was proportional to the fluid circulation velocity in the pump, but as the nozzle diameter increased, the suction volume decreased. The Rahman [9] experiment found that nozzle geometry affected the gas entrainment rate and pressure drop in the pump and that a low nozzle coefficient could form a higher vacuum in the pump. Sharma [12] designed different shapes of nozzles for experiments and analyzed and compared the performance of LGJPs of various shapes. Sung [1] compared the entrainment flow of the LGJP in three installation modes: horizontal, vertical upward and vertical downward and found that the gas entrainment rate installed vertically downward was the best. Liu [13] observed the flow process in the pump and measured the pressure distribution in the pipe through experiments. Based on the expression of American scholars, he supplemented the expression for the optimal throat length and proposed that the isothermal compression efficiency during vacuum pumping could reach 20~50% of the optimal parameter design of the LGJP. Liao [14] studied the performance of the LGJP through experiments and at the same time, used a method of numerical simulation to analyze the variation law and interaction of various parameters in the LGJP. He measured and recorded the pressure of the LGJP and flow data under different area ratios, and the influence of the area ratio on the inspiratory performance was determined by analysis. Gao [15][16] used geometric parameters and working parameters, such as nozzles with different diameters, area ratio, throat distance and pulse frequency, to test the liquid–gas piston pulse jet pump and preliminarily mastered the stable conditions of the device operation. Ge [19] proposed that when the throat-to-nozzle distance of the LGJP remained unchanged, the pressure ratio gradually decreases with the increase in the flow ratio. When the throat distance was 1.5 times the nozzle diameter, the efficiency of the LGJP was the highest, and the optimal throat distance range of the LGJP was determined to be 1.0 to 1.7 times the nozzle diameter.
Bhatkar [20] experimentally studied the performance parameters of the LGJP. The results showed that the working efficiency increased with the increase in the flow ratio and decreased with the decrease in the pressure ratio. Wu [21] conducted experiments under the same orifice Reynolds number and different liquid–gas flow ratio. The experiments showed that the bubble size in the pump was inversely proportional to the flow ratio, and the bubble diameter significantly changed at a low Reynolds number but changed little at a high Reynolds number. Eisallak [22] experimentally analyzed the influence of inlet pressure on jet flow. The results showed that the performance of LGJP was improved when the inlet pressure was weak, and the pump efficiency was reduced when the inlet pressure was strong. Mikheev [23] conducted an experimental analysis on the nozzle and capacity curve of the LGJP in the working environment where the inlet pressure was greater than 1 MPa. Zhang [24] put forward the scheme of using the LGJP to recover casing gas and emphasized that the optimal distance between the nozzle and throat of the LGJP is different under different working fluid pressures.
Carvalho [25] carried out numerical simulation research on the flow field of two-phase fluid in the throat of the LGJP with CFD software on the computer. Jiao [26] analyzed the mathematical model of the LGJP, synthesized the empirical resistance coefficients of each structure of the LGJP as a dimensionless undetermined coefficient, determined its undetermined coefficient through a large number of experiments and obtained the correlation function expression. The mathematical model of single-phase flow was extended, and the mathematical model of two-phase flow of the LGJP was determined. At the same time, the results of multiple numerical simulations showed that compared with the single-phase flow model, the mathematical model of two-phase flow was more accurate in analyzing and comparing the performance of the LGJP. Ismagilov [27] measured the performance of the LGJP and analyzed its characteristics by discussing the physics of the LGJP and establishing a mathematical model. Sharma [28] conducted a simulation analysis on the influence of the turbulent flow effect in the CFD model on the internal flow and gas entrainment rate of the LGJP to optimize the design of the pump. Zhu [29] studied the influence of the structure size on the suction performance of the LGJP and used the CFD numerical simulation method to study the relationship between the structural parameters of the nozzle area ratio, the throat, the nozzle distance, the throat length and the suction performance, respectively. Finally, the optimal range of each structure size under the highest efficiency was given. Semlitsch [30] proposed that four alternative jet pump configurations have been explored, i.e., a chevron primary nozzle, an empirical primary nozzle, a primary nozzle with swilling inserts and a multiple injector nozzle. The simulation found that, with the chevron primary nozzle, the jet pump efficiency with the chevrons slightly increased (less than one percent). Using an elliptical primary nozzle, the diffuser was only partially better utilized with an elliptical primary jet pipe exit, but an improvement of the jet pump efficiency of approximately two percent was achieved. With the primary nozzle with swirling inserts, the ratio of flow momentum to mixing could be manipulated with an increase in guide vane height to optimize the primary jet structure. The efficiency of the jet pump increased by about 6% using a multiple injector nozzle. Zheng [31] used a numerical simulation to simulate the internal flow field of the LGJP and found that with the increase in the liquid flow rate and the diameter of the diffuser outlet, the pressure dropped at the jet outlet and increased at the inlet of the jet pump accordingly. In addition, the wall flow effect increased, and the working efficiency decreased. Qin [32] pointed out that the appropriate liquid inlet speed can stabilize the volume fraction of each phase in the LGJP, which is conducive to the normal injection of the ejector. The increase in the output pressure of the diffuser leads to steam liquefaction and affects the normal operation of the ejector. Gao [33] conducted a three-dimensional numerical simulation calculation on the throat cavity contraction half angle of different LGJPs. It was found that the variation trend of the efficiency of the LGJP with the contraction half angle was similar to that of the pressure ratio, and there was a maximum value. The optimal suction efficiency interval was determined according to the reduction in the maximum suction efficiency by 5%, and the optimal range of the corresponding throat contraction half angle was 13.5°~17.1°. Wang [34] simulated the mixed flow in a LGJP and divided the mixing process into three stages: coaxial flow, mixed shock flow and bubble flow. The mixed shock wave was the main factor affecting the mixed flow characteristics and the performance of the LGJP.
Yang [35][36][37][38] designed the diffuser of the jet pump using the method of constant speed or constant pressure change, studied the influence of structural parameters on the internal flow field and found, through analysis that compared with the traditional conical diffuser, that the diffuser with constant speed or constant pressure change obtained a better performance and significantly shortened the length of the jet pump. There was an optimal combination of throat and diffuser. In order to improve the performance of an annular jet pump, the constant velocity/pressure rate of change method was used to design its diffuser, and the results showed that the prediction results of the RNG k-ε turbulence model were in better agreement with the experimental data than the standard, and this is an achievable k-ε turbulence model.
Sato [39] used high-speed camera technology to observe the whole process of cavitation generation, development and collapse in the Venturi and observed the unstable sheet-like cavitation cloud in the diffusion section under a small cavitation number. Stutz [40] observed the unstable sheet-like cavitating cloud of a Venturi tube with an X-ray device and dual light detector, found that the change in the cavitating cloud volume with time characterized the periodic law of cavitating cloud shedding and pointed out that the exit velocity had an important impact on the cavitating flow and the frequency of cavitating cloud shedding. Coutier [41][42] carried out a numerical simulation of the unstable cavitating flow in rectangular Venturi, and the obtained results are in good agreement with the test results of Stutz [40].
In order to improve the accuracy of the unsteady cavitation simulation of hydrofoil, Gu [43][44][45] used the GCI evaluation method to study grid independence and dispersion error to determine the optimal number of grids and reveal the mechanism of instability and falling off of hydrofoil cavitation. Yazici [46] studied the cavitating flow in the two-dimensional axisymmetric Venturi, found that the vibration frequency range of the cavitating flow was wide and observed that the high momentum bubbles eventually collapsed into small low momentum bubbles in the diffusion tube, and the vibration became smaller. Sayyaadi [47] observed the fluctuating process of the cavitating flow in Venturi using a high-speed camera and found that compared with the working pressure, the cavitating number had a more significant impact on the pulsating frequency, eigenfrequency and dimensionless parameter st of the length of the cavitating cloud and believed that the return jet was the main factor for cavitating cloud shedding. Xu [48] studied the influence of the area ratio of the diffuser inlet to the nozzle outlet, the volume of the displacement container and the configuration of the suction gap on the performance of the Venturi counter flow diverter pumping system. The RFD system with an area ratio greater than 1 showed a higher efficiency, and the reduction in the volume pressure around the jet core led to cavitation, which led to a reduction in the lifting efficiency.

References

  1. Kumar, R.S.; Mani, A.; Kumaraswamy, S. Analysis of a jet-pump-assisted vacuum desalination system using power plant waste heat. Desalination 2005, 179, 345–354.
  2. Neve, R.S. The performance and modeling of liquid jet gas pumps. Int. J. Heat Fluid Flow 1988, 9, 156–164.
  3. Carvalho, P.M. Modeling the Electrical Submersible Jet Pump Producing High Gas-Liquid-Ratio Petroleum Wells. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 1998.
  4. Neve, R.S. Diffuser performance in two-phase jet pumps. Int. J. Multiph. Flow 1991, 17, 267–272.
  5. Lu, H. Theory and Application of Jet Pump Technology; Water Conservancy and Electric Power Press: Beijing, China, 1989.
  6. Lu, H. Theory and Application of Jet Technology; Wuhan University Press: Wuhan, China, 2004.
  7. Liao, D.; Lu, H. Research on basic performance and correction coefficients of liquid-liquid gas jet pump. Chin. J. Hydrodyn. 1996, 12, 610–617.
  8. Haidl, J.; Mařík, K.; Moucha, T.; Rejl, F.J.; Valenz, L.; Zednikova, M. Hydraulic characteristics of liquid–gas ejector pump with a coherent liquid jet. Chem. Eng. Res. Des. 2021, 168, 435–442.
  9. Rahman, F.; Umesh, D.; Subbarao, D.; Ramasamy, M. Enhancement of entrainment rates in liquid–gas ejectors. Chem. Eng. Process. Process Intensif. 2010, 49, 1128–1135.
  10. Opletal, M.; Novotný, P.; Linek, V.; Moucha, T.; Kordač, M. Gas suction and mass transfer in gas-liquid up-flow ejector loop reactors. Effect of nozzle and ejector geometry. Chem. Eng. J. 2018, 353, 436–452.
  11. Kim, M.I.; Kim, O.S.; Lee, D.H.; Kim, S.D. Numerical and experimental investigations of gas–liquid dispersion in an ejector. Chem. Eng. Sci. 2007, 62, 7133–7139.
  12. Sharma, V.P.; Kumaraswamy, S.; Mani, A. Effect of various nozzle profiles on performance of a two-phase flow jet pump. Int. J. Mech. Aerosp. Ind. Mechatron. Manuf. Eng. 2012, 1, 173–179.
  13. Liu, J. Experimental Research on performance of liquid-air jet pump. J. Wuhan Inst. Water Conserv. Electr. Power 1982, 3, 105–114.
  14. Liao, D.; Lu, H. Study on basic performance and correction coefficients of liquid-liquid gas jet pump. Fluid Mach. 1997, 4, 26–29.
  15. Gao, C.; Wang, Y. Research and application progress of liquid-gas jet pump. China Pet. Mach. 2008, 2, 67–70.
  16. Zhang, J.; Gao, C.; Yan, Y.; Wang, X. Pulsed liquid-air jet pump energy balance. J. Drain. Irrig. Mach. 2012, 30, 422–427.
  17. Witte, J.H. Mixing Shocks and Their Influence on the Design of Liquid-Gas Ejectors. Master’s Thesis, Delft University, Delft, The Netherlands, 1962.
  18. Cunningham, R.G. Liquid jet pumps for two-phase flows. J. Fluids Eng. 1995, 117, 309–316.
  19. Ge, Y.; Ge, Q.; Yang, J. Numerical simulation of throat distance of liquid-gas jet pump and its optimal range determination. Fluid Mach. 2012, 40, 21–24.
  20. Bhatkar, V.; Sur, A. An experimental analysis of liquid air jet pump. Front. Heat Mass Transf. (FHMT) 2021, 17, 12.
  21. Wu, Y.L.; Xiang, Q.J.; Li, H.; Chen, S.X. Study on bubble sizes in a down-flow liquid jet gas pump. IOP Conf. Ser. Earth Environ. Sci. 2012, 15, 052017.
  22. Eisallak, M.; Hefny, M.M. Experimental investigation of the performance of liquid gas jet pumps with inlet swirling. Proc. Inst. Mech. Eng. Part A J. Power Energy 2010, 224, 363–372.
  23. Mikheev, N.I.; Davletshin, I.A.; Mikheev, A.N.; Kratirov, D.V.; Fafurin, V.A. Efficiency of liquid-jet high-pressure booster compressors. J. Phys. Conf. Ser. 2017, 891, 012202.
  24. Zhang, Y.; Zhao, J.; Liu, Z.; Zuo, P.; Kwabena, A.R. Numerical simulation and parameter study of ejector in casing gas recovery system. J. Mech. Sci. Technol. 2021, 35, 2689–2696.
  25. Choi, S.H.; Ji, H.S.; Kim, K.C. Comparative study of hydrodynamic characteristics with respect to direction of installation of gas-liquid ejector system. J. Mech. Sci. Technol. 2015, 29, 3267–3276.
  26. Jiao, B.; Blais, R.N.; Schmidt, Z. Efficiency and pressure recovery in hydraulic jet pumping of two-phase gas/liquid mixtures. SPE Prod. Eng. 1990, 5, 361–364.
  27. Ismagilov, A.R.; Spiridonov, E.K. Operational process and characteristics of liquid-gas jet pumps with the ejected vapor-gas medium. Procedia Eng. 2016, 150, 247–253.
  28. Sharma, D.; Patwardhan, A.; Ranade, V. Effect of turbulent dispersion on hydrodynamic characteristics in a liquid jet ejector. Energy 2018, 164, 10–20.
  29. Chen, L.; Liu, S. Numerical simulation of internal flow field of pulsed liquid-gas jet pump. Machinery 2013, 8, 29–31.
  30. Semlitsch, B. Large Eddy Simulation of Turbulent Compressible Jets. Ph.D. Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2014.
  31. Zheng, P.; Qin, J.; Chen, X. Numerical simulation and optimization of gas-liquid ejector ejection performance. J. Jiangsu Univ. (Nat. Sci. Ed.) 2017, 38, 30–36.
  32. Qin, J.; Zheng, P.; Chen, X. Numerical simulation of gas-liquid ejector jet performance under different inlet and outlet conditions. Chin. J. Process Eng. 2017, 17, 469–476.
  33. Gao, G.; Xing, Y.; Wang, Y. Numerical study on the influence of the constriction half angle of the throat segment on the flow field characteristics of a liquid-air jet pump. Chin. J. Vac. Sci. Technol. 2020, 40, 174–179.
  34. Wang, X.; Li, H.; Dong, J.; Wu, J.; Tu, J. Numerical study on mixing flow behavior in gas-liquid ejector. Exp. Comput. Multiph. Flow 2021, 3, 108–112.
  35. Yang, X.; Long, X.; Kang, Y.; Xiao, L. Application of constant rate of velocity or pressure change method to improve annular jet pump performance. Int. J. Fluid Mach. Syst. 2013, 6, 137–143.
  36. Wang, X.; Yang, X.; Long, X.; Zhou, D. Application of constant rate of velocity change method to improve dust cleaning performance. Disaster Adv. 2013, 6, 459–468.
  37. Xiao, J.; Wu, Q.; Chen, L.; Ke, W.; Wu, C.; Yang, X.; Yu, L.; Jiang, H. Assessment of different CFD modeling and solving approaches for a supersonic steam ejector simulation. Atmosphere 2022, 13, 144.
  38. Yang, X.; Long, X.; Kang, Y.; Xiao, L. Effect of diffuser structure and throat length on jet pump performance. J. Harbin Inst. Technol. 2014, 46, 111–115.
  39. Sato, K.; Hachino, K.; Saito, Y. Inception and dynamics of traveling-bubble-type cavitation in a venturi. In Proceedings of the ASME/JSME 2003 4th Joint Fluids Summer Engineering Conference, Honolulu, HI, USA, 6–10 July 2003; Volume 36967, pp. 279–285.
  40. Stutz, B.; Legoupil, S. X-ray measurements within unsteady cavitation. Exp. Fluids 2003, 35, 130–138.
  41. Coutier Delgosha, O.; Reboud, J.; Delannoy, Y. Numerical simulation of the unsteady behaviour of cavitating flows. Int. J. Numer. Methods Fluids 2003, 42, 527–548.
  42. Coutier Delgosha, O.; Fortes Patella, R.; Reboud, J.L. Evaluation of the turbulence model influence on the numerical simulations of unsteady cavitation. J. Fluids Eng. 2003, 125, 38–45.
  43. Gu, Y.; Ma, L.; Yan, M.; He, C.; Zhang, J.; Mou, J.; Wu, D.; Ren, Y. Strategies for improving friction behavior based on carbon nanotube additive materials: A review. Tribol. Int. 2022, 228, 107490.
  44. He, C.; Gu, Y.; Zhang, J.; Ma, L.; Yan, M.; Mou, J.; Ren, Y. Preparation and modification technology analysis of Ionic Polymer-Metal Composites (IPMCs). Int. J. Mol. Sci. 2022, 23, 3522.
  45. Gu, Y.; Zhang, J.; Yu, S.; Mou, C.; Li, Z.; He, C.; Wu, D.; Mou, J.; Ren, Y. Unsteady numerical simulation method of hydrofoil surface cavitation. Int. J. Mech. Sci. 2022, 228, 107490.
  46. Yazici, B.; Tuncer, I.; Ak, M. Numerical & experimental investigation of flow through a cavitating venturi. In Proceedings of the 2007 3rd International Conference on Recent Advances in Space Technologies, Istanbul, Turkey, 14–16 June 2007; pp. 236–241.
  47. Sayyaadi, H. Instability of the cavitating flow in a venturi reactor. Fluid Dyn. Res. 2010, 42, 055503.
  48. Xu, C.; Huang, Y. Experimental characteristics of pneumatic pulse jet pumping systems with a Venturi-like reverse flow diverter. Int. J. Chem. React. Eng. 2011, 9, A34.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Engineering, Mechanical
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Huiyan Zhang
,
Daohang Zou
,
Xuelong Yang
,
Jiegang Mou
,
Qiwei Zhou
,
Maosen Xu
View Times: 785
Revisions: 2 times (View History)
Update Date: 03 Feb 2023
Table of Contents
    1000/1000
    Hot Most Recent
    Video Production Service
    Feedback