Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Yaping Ren
 -- 3052 2023-01-12 10:27:11 |
2 layout
Camila Xu
 Meta information modification 3052 2023-01-12 10:47:04 |

Video Upload Options

We provide professional Video Production Services to translate complex research into visually appealing presentations. Would you like to try it?
No, upload directly Yes

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Ren, Y.;  Lu, X.;  Guo, H.;  Xie, Z.;  Zhang, H.;  Zhang, C. Facility Location and Vehicle-Routing Problem in Reverse Logistics. Encyclopedia. Available online: https://encyclopedia.pub/entry/40108 (accessed on 15 November 2024).
Ren Y,  Lu X,  Guo H,  Xie Z,  Zhang H,  Zhang C. Facility Location and Vehicle-Routing Problem in Reverse Logistics. Encyclopedia. Available at: https://encyclopedia.pub/entry/40108. Accessed November 15, 2024.
Ren, Yaping, Xinyu Lu, Hongfei Guo, Zhaokang Xie, Haoyang Zhang, Chaoyong Zhang. "Facility Location and Vehicle-Routing Problem in Reverse Logistics" Encyclopedia, https://encyclopedia.pub/entry/40108 (accessed November 15, 2024).
Ren, Y.,  Lu, X.,  Guo, H.,  Xie, Z.,  Zhang, H., & Zhang, C. (2023, January 12). Facility Location and Vehicle-Routing Problem in Reverse Logistics. In Encyclopedia. https://encyclopedia.pub/entry/40108
Ren, Yaping, et al. "Facility Location and Vehicle-Routing Problem in Reverse Logistics." Encyclopedia. Web. 12 January, 2023.
Facility Location and Vehicle-Routing Problem in Reverse Logistics
Edit
This entry is adapted from the peer-reviewed paper 10.3390/math11020298

The concept of reverse logistics (RL) was put forward in 1992, whose essence was to transfer end-of-life (EOL) products from the consumer to the producer for processing.

reverse logistics remanufacturing EOL product

1. Introduction

Reverse logistics (RL) and remanufacturing are the two main processes for end-of-life (EOL) products’ recovery, aiming to maximize resource utilization by means of collecting, disassembling, refurbishing, and reassembling to grant the EOL products the same quality and functionality as new products. In order to improve the efficiency of product recovery, it is vital to solve the combinatorial optimization problems (COPs) involved effectively; therefore, scholars have conducted much research on them.
The concept of RL was put forward by Stock [1] in 1992, whose essence was to transfer EOL products from the consumer to the producer for processing. The COPs in RL include facility location and the vehicle-routing problem (VRP). The facility location is to build an appropriate network structure to determine the location of various facilities, such as collection centers, remanufacturing centers, distribution centers, etc. The VRP is to formulate a specific transportation plan to transport EOL products to the above facilities, including the driving path, number of vehicles, types of vehicles, etc. There are some reviews about the facility location and VRP in RL [2][3][4][5].
However, only the transportation process of RL cannot truly realize the reuse of resources; remanufacturing is the key to achieve sustainable development [6]. Remanufacturing is a process to recover EOL products to the same state as new products through inspection, disassembly, cleaning, maintenance, replacement, reassembly, etc. [7]. The COPs involved include disassembly sequence planning (DSP), disassembly-line-balancing problem (DLBP), disassembly scheduling, production scheduling, reassembly, etc. There are also some reviews about each of the COPs in remanufacturing [8][9][10][11].

2. Facility Location and VRP in RL

Before remanufacturing EOL products, collecting them from users is the first step, which is essentially a process of RL. To perform this efficiently, it is necessary to properly plan the location of various facilities and products’ flow routes. Specifically, companies need to choose how to collect EOL products from users and transport them to collection centers, where to inspect EOL products, where to remanufacture EOL products to make them available for resale, and how to sell remanufactured products to potential users [12]. That is to solve the problem of facility location and the VRP in RL.

2.1. Facility Location in RL

Generally, the facility location determines the location of the collection center, remanufacturing center, distributing center, and so on to minimize the logistics costs. Scholars have designed different network structures based on these facilities, which can be summarized as three types. This section will analyze the three kinds of network structures from the perspective of mathematical models, including: general network structure, closed-loop network structure, and hybrid network structure.

2.1.1. General Network Structure

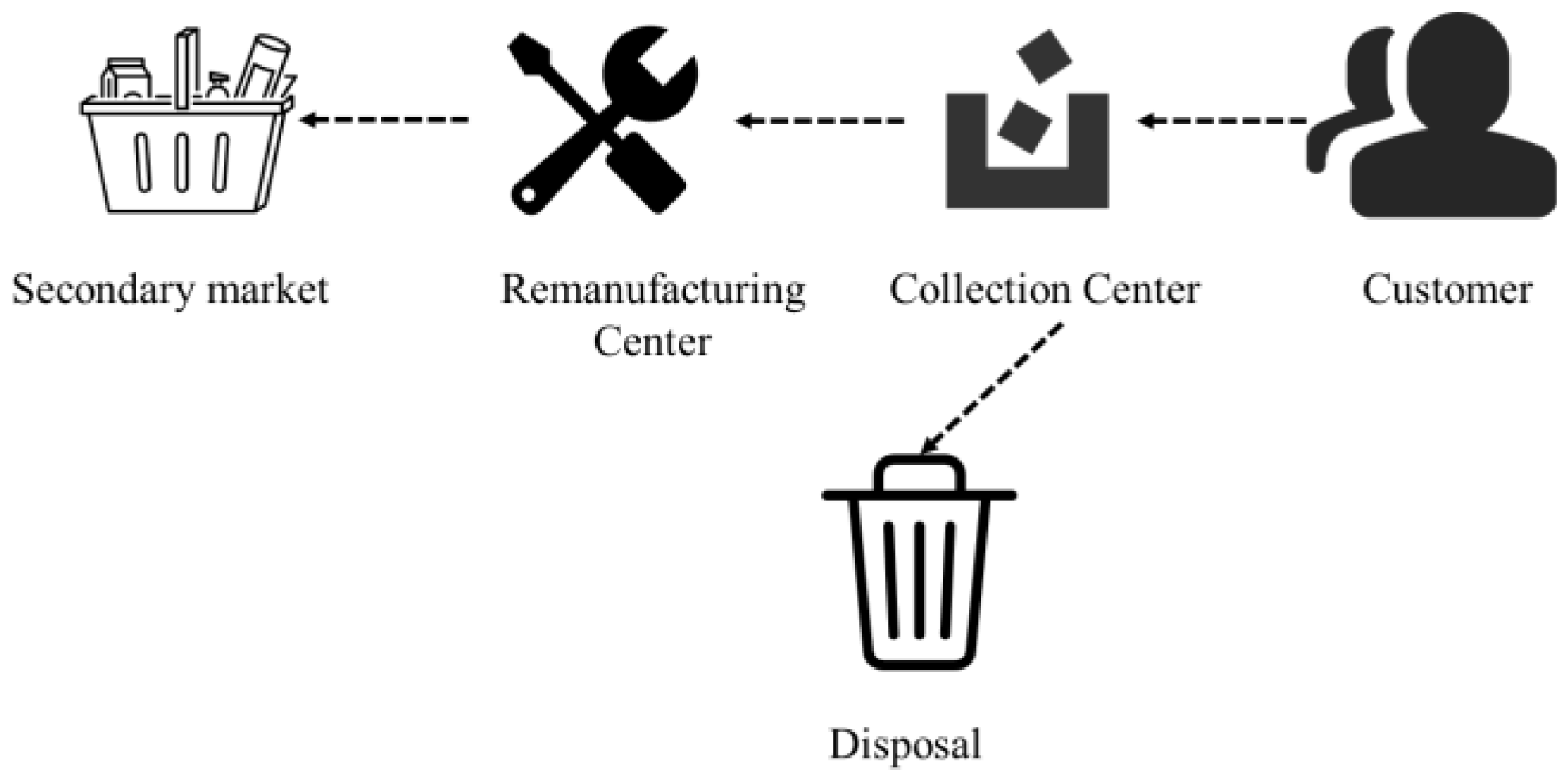
The general network structure consists of four parts: consumers, collection centers, remanufacturing centers, and secondary markets, as shown in Figure 1. The collection center collects EOL products from consumers, inspects and disassembles the products, and then, according to the value of the components, chooses to discard or remanufacture; finally, the remanufactured finished products flow back to the market for sale. It is worth noting that in this network structure, remanufactured products are usually different from new products and mainly flow to the second-hand market.
Mathematics 11 00298 g001
Figure 1. General network structure.
It can be seen from Table 1 that most researchers choose the single-objective mixed-integer linear programming (MILP) model when establishing the mathematical model of the general network structure. Two papers established the mixed-integer nonlinear programming model (MILNP) [13][14], and they were single-objective optimization to maximize the total profit or minimize the total cost [14][15][16][17][18][19][20]. However, while minimizing the total cost, Roghanian and Pazhoheshfar [21] considered the uncertainty of capacity, demand, and product quantity in RL parameters, so they proposed a probabilistic mixed-integer linear programming model (P-MILP) and converted it into an equivalent deterministic model when solving. Tari and Alumur [22] considered the fairness between different companies and the problem of providing a stable product flow for each company while minimizing the total cost, thus establishing multi-objective mixed-integer linear programming (M-MILP).
Table 1. Mathematical model of general network structure.
NO Years Type Num. of Objectives Products Solution
[13] 2010 MINLP One (maximize profit) Tire retreading Lingo 8.0
[15] 2012 MILP One (maximize profit) Washing machines
and tumble dryers		 CPLEX
[21] 2014 P-MILP One (minimize the total cost) Hypothetical problem Genetic algorithm
[22] 2014 M-MILP Three (minimize total cost, ensure equity among different firms, and provide stable product flow to each company within the planning scope) Electrical waste and electronic equipment CPLEX
[16] 2015 MILP One (maximize profit) Washing machines
and tumble dryers		 CPLEX
[17] 2016 MILP One (maximize profit) Vehicles CPLEX
[18] 2017 MILP One (maximize profit)   Genetic algorithm
[14] 2018 MINLP One (maximize profit) Waste recycling Hybrid genetic algorithm
[19] 2019 MILP One (minimize the total cost) Lithium-ion batteries Three-phase heuristic
[20] 2020 MILP One (maximize profit) Numerical research CPLEX
In addition to minimizing the total cost and maximizing the total profit, the main purpose of establishing the mathematical model is to find out the location, capacity, and quantity of the core facilities, such as the collection center and the remanufacturing center that need to be opened in the RL network. Sasikumar et al. [13] provided decisions related to the number and location of facilities to be opened and the allocation of corresponding product flows through the establishment of MILP. Roghanian and Pazhoheshfar [21] proposed a multi-product, multi-stage RL network problem. It was not only necessary to determine the subset of disassembly centers and machining centers to be opened, but also necessary to determine the transportation strategy to meet the needs of manufacturing centers and recycling centers, with the minimum fixed opening cost and total transportation cost. Alshamsi and Diabat [16] also introduced important transportation considerations by providing options for using internal fleets and outsourcing options. Liao [14] introduced a modular remanufacturing process and emission reduction; two papers [14][16] also considered the carbon footprint while determining the location of factories (inspection/remanufacturing), the transportation of cores/remanufactured products between factories, and the route of vehicles between factories.

2.1.2. Closed-Loop Network Structure

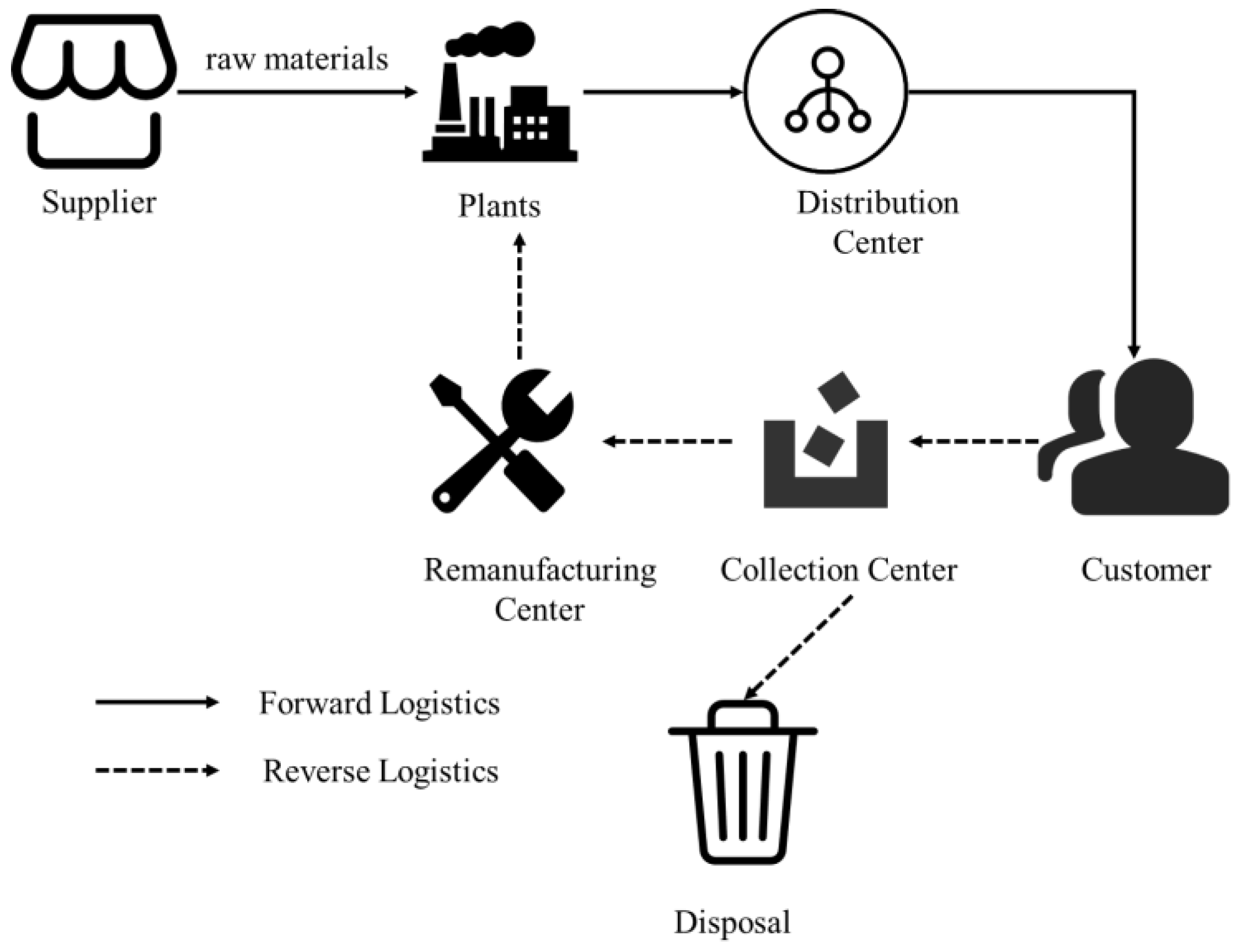
To protect the environment, many countries expand producer responsibility through legislation. Driven by economic benefits, many manufacturers began to integrate RL [23], thus evolving a closed-loop network structure (CLNS), as shown in Figure 2. The CLNS integrates forward logistics and reverse logistics, producing huge economic and environmental benefits, and is the most widely studied network structure by scholars. In the CLNS, manufacturers obtain raw materials from suppliers, and the products manufactured are sold to customers through distributors. The products used by customers are collected by the collection center and selectively sent to the remanufacturing center. After remanufacturing, they return to forward logistics. In the CLNS, the terminals of forward logistics and reverse logistics are the same customer group.
Mathematics 11 00298 g002
Figure 2. Closed-loop network structure.
Table 2 and Table 3 are, respectively, the previous mathematical model research on CLNS and the corresponding abbreviations of terms. In paper [24], the environmental problems are integrated into an integer CLNS model, and a genetic algorithm based on the spanning tree structure is proposed to solve the NP-hard problem. Pishvaee et al. [25] also established a multi-objective fuzzy mathematical model to design the environmental protection supply chain. They used life cycle assessment to quantify the environmental impact of the network. Zohal and Soleimani [26] also regard the model as a green CLNS according to the CO2 emissions of the gold industry. As shown in Table 2, most scholars are studying how to use metaheuristics and heuristic algorithms to solve the model. Devika et al. [27] proposed six different mixed metaheuristics to solve the sustainable CLNS problem they developed. In paper [28], a CLNS decision model under uncertainty was proposed, and the imperialist competitive algorithm, particle swarm optimization, and genetic algorithm were used to solve the large-scale NP-hard model developed by them. In another study, Fard et al. [29] considered the three-level decision model to express their forward/reverse supply chain network design problem, and adopted a variety of metaheuristic algorithms, including tabu search, variable neighborhood search, particle swarm optimization, water wave optimization, and Keshtel algorithm. The results show that the metaheuristic algorithm is an effective method to solve the model in practice.
Table 2. Mathematical model of CLNS.
NO Years Type Objectives Network Stages Solution Outputs
[24] 2010 MILP MC, MEI SC, PC, DC, CZ, RYC E FL, PA, I, PT, TM, CR
[30] 2011 MILP MC, MEI, MS SC, PC, DC, CZ, CC, RDC, RCC, RMC, RYC, DIC OM SO, FL, A, PA, PT, TA, NP
[31] 2012 SMIP MC SC, PC, DC, CZ, CC, RDC, RCC, RMC, RYC, DIC OM SO, FL, A, PA, PT, TA, NP
[25] 2012 MILP MC PC, DC, RCC OM FL, FC, A, PA
[27] 2014 FMIP MC, MEI PC, CZ, CC, RCC (Steel), RCC(Plastic), DIC IFS FL, TA, PA, NP
[32] 2015 SMIP MC CZ, CZ, CC, RDC, RCC, DIC E FL, TA, QND
[26] 2016 MINLP MC SC, PC, CZ, W, DC, RMC, RCC E, OM FC, TA, UP, I, NP
[28] 2017 MILP MC SC, PC, DC, CZ, D, RMC, RDC, DIC GA FL, PA, TA
[29] 2018 MILP MC, MEI CC, DC, CZ, SC, RYC OM FL, A, NP, CS, TA
[33] 2019 MINLP MC, MEI, MS SC, PC, DC, CZ, CC, RDC, RCC, RMC, RYC, DIC OM SO, FL, A, PA, PT, TA, NP, DC
Table 3. Abbreviations comparison table.
Item Content Notation
Objectives Min cost/max profit MC
  Min environment impacts MEI
  Max social benefits MS
Network Stages Supply centers SC
  Production centers PC
  Distribution centers DC
  Warehouses W
  Customer zones (retail outlets) CZ
  Collection/inspection centers CC
  Dismantlers D
  Redistribution centers RDC
  Recovering centers RCC
  Remanufacturing centers RMC
  Recycling centers RYC
  Disposal/incineration centers DIC
Solution Method Exact E
  Genetic-algorithm-based GA
  Other metaheuristics OM
  Interactive fuzzy solution approach IFS
Outputs Suppliers/orders SO
  Facilities location FL
  Facility capacity FC
  Allocation A
  Discount DC
  Production amount PA
  Utilization of production centers UP
  Production technology PT
  Transportation amount TA
  Transportation mode TM
  Number of vehicles NV
  Inventory I
  Number of used products which are processed NP
  Carbon credits sold/purchased CS
  Quantity of non-satisfied demand QND

2.1.3. Hybrid Network Structure

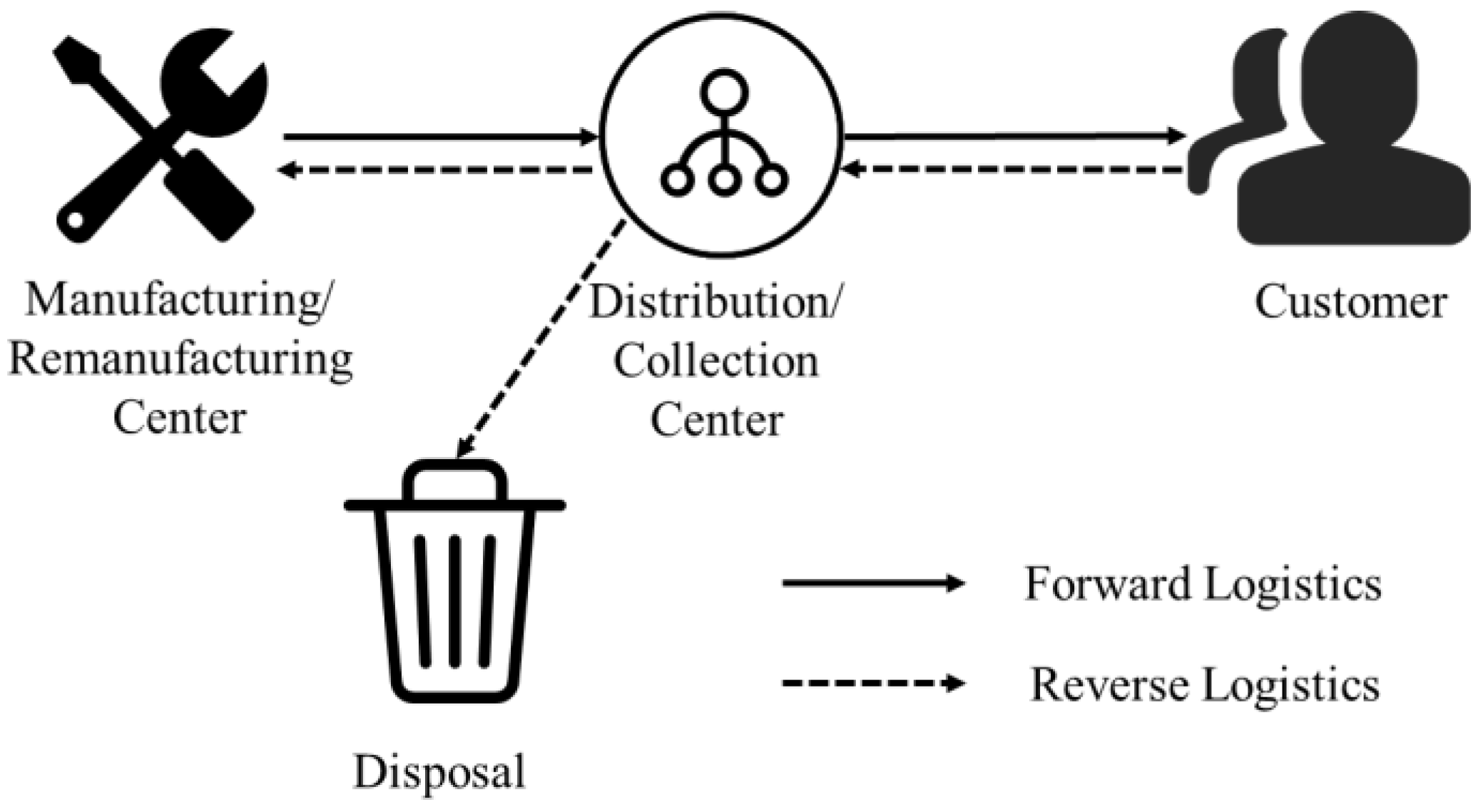
Some scholars have put forward the concept of hybrid facilities, that is, the merger of a manufacturing center and remanufacturing center, and the merger of a distribution center and collection center, as shown in Figure 3, thus representing integrated forward and reverse logistics [34]. Due to the existence of mixed facilities, RL can use the nodes of forward logistics to optimize its design, thereby effectively reducing or eliminating the cost of building new RL networks. Therefore, in recent years, it has also become a research hotspot of scholars.
Mathematics 11 00298 g003
Figure 3. Hybrid network structure.
In this growing research field, the number of literature sources is growing rapidly. Fleischmann et al.’s pioneering work in hybrid network structure modeling studied the impact of product recycling on the design of a logistics network [35]. The study argued that the impact of product recycling depended heavily on the environment. In some cases, it may be feasible to integrate this activity into the existing logistics structure, while in other cases, it may be necessary to redesign the logistics network in an overall manner. Since this research, Salma et al. [36] incorporated capacity constraints, demand uncertainty, and returns into the multi-product planning based on this model. Later, they integrated strategic and tactical decisions by considering two inter-related time scales: at the strategic level, they gave a discretization of the time range, which must meet the needs and reporting values; at the tactical level, more detailed planning was allowed to achieve this goal [37]. Cardoso et al. [38] analyzed the integration of RL activities under demand uncertainty, took the maximum expected net present value as the objective function, and made decision variables for facility size and location, process installation, forward and reverse logistics, and inventory level. Later, the author expanded this work to solve the uncertainty and characterize the elastic closed-loop network structure [39].
Subsequently, environmental and social sustainability issues began to be considered. Paksoy et al. [40] analyzed the supply plan and considered the emission cost (total cost minimization) and the profit maximization of the recycled products in the economic objective function. Mota et al. [41] considered the sustainability of the economy, environment, and society. They proposed a mathematical model with the minimization of the total cost of the network structure as the economic objective function; the minimization of the life cycle assessment index ReCipe as the environmental objective function; and the location of the network structure activities in underdeveloped areas as the social objective function. Gao et al. [42], based on the existing forward logistics network, proposed a double-objective stochastic integer programming model aiming at economic and environmental benefits, which aimed to support production, remanufacturing, and waste activities by addressing the uncertainty factors of new product demand and the return volume of old products in the customer area.

2.2. VRP in RL

After locating critical facilities, the next question is how to reversely transport EOL products, that is, the vehicle-routing problem in RL. The VRP in RL refers to how to arrange vehicle types, quantities, capacities, routes, etc., to collect waste products from customers, to achieve the goal of the minimum cost or the shortest route. Collection is the starting point of EOL product recovery, so scholars have carried out much research to improve the efficiency of this link.
The VRP in RL can be described as: a certain number of customers must use a certain number of fleets with limited capacity, which are usually assumed to be the same. The vehicles are stationed in a central parking lot and return after collecting waste products from customers according to the route requirements. Cao et al. [43] used RL to reuse the Internet of Things through identifying the resources required for road infrastructure, and modeled RL to transfer the Internet of Things from a tailings dam to a processing plant, and then to a road construction site. For minimizing the total cost, Richnák and Gubová [44] established a heterogeneous-fleet electric-vehicle path-recovery time window model considering vehicle load constraints. The type of vehicle limited the weight of recyclable waste and the time limit allowed by the customer. Chen et al. [45] proposed a nonlinear programming model including the number of second-hand products and reprocessed products. For both types of requirements, analysis and insight were provided in the form of a complete strategy consisting of different scenarios that allow optimal decisions to be made under a variety of conditions. Through sensitivity analysis, numerical examples supplemented the understanding of the model. Santana et al. [46] considered the risks in the e-waste recycling process and modeled the reverse logistics process of electrical and electronic equipment as a MILP with biological objectives under uncertainty. The cooperative alliance strategy was employed by Mishra et al. [47] to actualize the constrained capabilities of VRP in RL. The cooperative mechanism made it possible to prevent inefficient resource distribution, cut back on circular logistics, and minimize long-distance travel. In order to minimize recovery tasks, Chen et al. [48] used an improved ant colony algorithm to handle vehicle design and route optimization problems. Foroutan et al. [49] established a mixed-integer nonlinear programming model for multi-mode green vehicle routing and scheduling with the objective of minimizing operating costs and environmental costs and considering return, lead time, and delay costs. A mathematical model for the recovery of EOL cars was developed by Chaabane et al. [50] by combining the traditional VRP with the receiving and delivery problem as well as the restrictions of various vehicle kinds and time periods.
The multi-vehicle routing optimization problem with time limitations has also been the subject of interest for scholars’ in-depth research. In order to meet the needs of minimizing transportation and procurement costs, the research in the literature [51] included choosing suppliers and setting up homogeneous fleets to buy various products from chosen suppliers. It also defined new branching rules, introduced new inequality families, and established the competitiveness of the new branching price-reduction method. To optimize the multi-depot production material-allocation system and research the routing problem of delivery vehicles, Xu et al. [52] took into account a variety of factors, including multiple warehouses, multiple vehicle types, multiple commodities, mismatches between customer supply and demand, and arbitrary segmentation of delivery and delivery demands. Fan et al. [53] designed a genetic variable neighborhood algorithm for multi-vehicle routing optimization problem with fuzzy set requirements by improving the adaptive search strategy. A multi-mode electric vehicle routing optimization model was developed by Guo et al. [54] taking into account the differentiating service costs under the consideration of vehicle diversity, charging strategy, person vehicle matching, and service time difference.
With the improvement in logistics network and the development of e-commerce, in order to improve customer satisfaction, logistics service providers need to handle a large number of delivery orders and return orders at the same time. In this case, the joint optimization of simultaneous pickup and delivery VRP (VRPSPD) can significantly improve the utilization rate of vehicles [55].
Studies have shown that solving the problem of collecting refurbished goods in forward and reverse logistics can improve the utilization rate of refurbished products, shorten the return time, and improve customer satisfaction [55]. Dethloff [56] studied VRPSPD in order to avoid redundant handling work, considering that customers have both picking and delivery needs. They developed an insertion-based heuristics method, which can be used to construct initial feasible solutions, which can be improved by subsequent application of the local search process. A specific case of VRPSPD that allows for the decomposition of the picking and delivery needs was developed by Masson et al. [57]. This method can be used in real-world transportation systems with many of pickup trucks but few deliveries. Nagy et al. [58] proposed a VRP with separable delivery and picking, and studied the cost reduction caused by demand segmentation of simultaneous delivery and pickup. In order to optimize vehicle scheduling to satisfy freight requests, Ghilas et al. [59] created a VRPSPD with scheduling lines and took synchronization and time window limitations into account in the solution algorithm. Gschwind et al. [60] evaluated the performance of branch cut and price algorithms in VRPSPD to solve the shortest path issue under time windows and resource limitation. Goeke [61] investigated the VRPSPD of electric cars, in which the route design of electric vehicles attempted to optimize the pick-up and delivery services in metropolitan areas with a lower environmental impact. Wolfinger [62] proposed a mixed-integer programming model to develop a single warehouse VRPPD with split load, and tested the algorithm performance through extensive computing experiments through large-scale neighborhood search. Haddad et al. [63] developed a multi-warehouse VRPPD to design a sustainable picking and distribution route between multiple warehouses. The efficiency of transportation can be increased at the same time, within the limitations of vehicle capacity and time window.

References

  1. Stock, J.R. Reverse Logistics: White Paper; Council of Logistics Management: Lombard, IL, USA, 1992.
  2. Zhang, X.; Zou, B.; Feng, Z.; Wang, Y.; Yan, W. A Review on Remanufacturing Reverse Logistics Network Design and Model Optimization. Processes 2021, 10, 84.
  3. Chanintrakul, P.; Coronado Mondragon, A.E.; Lalwani, C.; Wong, C.Y. Reverse logistics network design: A state-of-the-art literature review. Int. J. Bus. Perform. Supply Chain Model. 2009, 1, 61–81.
  4. Waidyathilaka, E.; Tharaka, V.K.; Wickramarachchi, A.P.R. Trends in Green Vehicle Routing in Reverse Logistics. In Proceedings of the International Conference on Industrial Engineering and Operations Management (IEOM), Bangkok, Thailand, 5–7 March 2019.
  5. Han, H.; Ponce Cueto, E. Waste collection vehicle routing problem: Literature review. PROMET Traffic Transp. 2015, 27, 345–358.
  6. Majumder, P.; Groenevelt, H. Competition in remanufacturing. Prod. Oper. Manag. 2001, 10, 125–141.
  7. Nasr, N.; Thurston, M. Remanufacturing: A key enabler to sustainable product systems. Rochester Instit. Technol. 2006, 23, 14–17.
  8. Laili, Y.; Li, Y.; Fang, Y.; Pham, D.T.; Zhang, L. Model review and algorithm comparison on multi-objective disassembly line balancing. J. Manuf. Syst. 2020, 56, 484–500.
  9. Zhou, Z.; Liu, J.; Pham, D.T.; Xu, W.; Ramirez, F.J.; Ji, C.; Liu, Q. Disassembly sequence planning: Recent developments and future trends. Proc. Instit. Mech. Eng. Part B J. Eng. Manuf. 2019, 233, 1450–1471.
  10. Morgan, S.D.; Gagnon, R.J. A systematic literature review of remanufacturing scheduling. Int. J. Prod. Res. 2013, 51, 4853–4879.
  11. Wang, Y.; Mendis, G.P.; Peng, S.; Sutherland, J.W. Component-oriented reassembly in remanufacturing systems: Managing uncertainty and satisfying customer needs. J. Manuf. Sci. Eng. 2019, 141, 021005.
  12. Fleischmann, M.; Bloemhof-Ruwaard, J.M.; Beullens, P.; Dekker, R. Reverse logistics network design. In Reverse Logistics; Springer: Berlin/Heidelberg, Germany, 2004; pp. 65–94.
  13. Sasikumar, P.; Kannan, G.; Haq, A.N. A multi-echelon reverse logistics network design for product recovery—A case of truck tire remanufacturing. Int. J. Adv. Manuf. Technol. 2010, 49, 1223–1234.
  14. Liao, T.Y. Reverse logistics network design for product recovery and remanufacturing. Appl. Math. Model. 2018, 60, 145–163.
  15. Alumur, S.A.; Nickel, S.; Saldanha-da-Gama, F.; Verter, V. Multi-period reverse logistics network design. Eur. J. Oper. Res. 2012, 220, 67–78.
  16. Alshamsi, A.; Diabat, A. A reverse logistics network design. J. Manuf. Syst. 2015, 37, 589–598.
  17. Demirel, E.; Demirel, N.; Gökçen, H. A mixed integer linear programming model to optimize reverse logistics activities of end-of-life vehicles in Turkey. J. Clean. Prod. 2016, 112, 2101–2113.
  18. Alshamsi, A.; Diabat, A. A Genetic Algorithm for Reverse Logistics network design: A case study from the GCC. J. Clean. Prod. 2017, 151, 652–669.
  19. Reddy, K.N.; Kumar, A.; Ballantyne, E.E.F. A three-phase heuristic approach for reverse logistics network design incorporating carbon footprint. Int. J. Prod. Res. 2019, 57, 6090–6114.
  20. Reddy, K.N.; Kumar, A.; Sarkis, J.; Tiwari, M.K. Effect of carbon tax on reverse logistics network design. Comput. Ind. Eng. 2020, 139, 106184.
  21. Roghanian, E.; Pazhoheshfar, P. An optimization model for reverse logistics network under stochastic environment by using genetic algorithm. J. Manuf. Syst. 2014, 33, 348–356.
  22. Tari, I.; Alumur, S.A. Collection center location with equity considerations in reverse logistics networks. INFOR Inf. Syst. Oper. Res. 2014, 52, 157–173.
  23. Zarei, M.; Mansour, S.; Husseinzadeh Kashan, A.; Karimi, B. Designing a reverse logistics network for end-of-life vehicles recovery. Math. Probl. Eng. 2010, 2010, 649028.
  24. Wang, H.F.; Hsu, H.W. A closed-loop logistic model with a spanning-tree based genetic algorithm. Comput. Oper. Res. 2010, 37, 376–389.
  25. Pishvaee, M.S.; Torabi, S.A.; Razmi, J. Credibility-based fuzzy mathematical programming model for green logistics design under uncertainty. Comput. Ind. Eng. 2012, 62, 624–632.
  26. Zohal, M.; Soleimani, H. Developing an ant colony approach for green closed-loop supply chain network design: A case study in gold industry. J. Clean. Prod. 2016, 133, 314–337.
  27. Devika, K.; Jafarian, A.; Nourbakhsh, V. Designing a sustainable closed-loop supply chain network based on triple bottom line approach: A comparison of metaheuristics hybridization techniques. Eur. J. Oper. Res. 2014, 235, 594–615.
  28. Fard, A.M.F.; Gholian-Jouybari, F.; Paydar, M.M.; Hajiaghaei-Keshteli, M. A bi-objective stochastic closed-loop supply chain network design problem considering downside risk. Ind. Eng. Manag. Syst. 2017, 16, 342–362.
  29. Fard, A.M.F.; Hajaghaei-Keshteli, M. A tri-level location-allocation model for forward/reverse supply chain. Appl. Soft Comput. 2018, 62, 328–346.
  30. Pishvaee, M.S.; Rabbani, M.; Torabi, S.A. A robust optimization approach to closed-loop supply chain network design under uncertainty. Appl. Math. Model. 2011, 35, 637–649.
  31. Chaabane, A.; Ramudhin, A.; Paquet, M. Design of sustainable supply chains under the emission trading scheme. Int. J. Prod. Econ. 2012, 135, 37–49.
  32. Soleimani, H.; Kannan, G. A hybrid particle swarm optimization and genetic algorithm for closed-loop supply chain network design in large-scale networks. Appl. Math. Model. 2015, 39, 3990–4012.
  33. Hajiaghaei-Keshteli, M.; Fathollahi Fard, A.M. Sustainable closed-loop supply chain network design with discount supposition. Neural Comput. Appl. 2019, 31, 5343–5377.
  34. Lee, D.H.; Dong, M.; Bian, W. The design of sustainable logistics network under uncertainty. Int. J. Prod. Econ. 2010, 128, 159–166.
  35. Fleischmann, M.; Beullens, P.; Bloemhof-Ruwaard, J.M.; Van Wassenhove, L.N. The impact of product recovery on logistics network design. Prod. Oper. Manag. 2001, 10, 156–173.
  36. Salema, M.I.G.; Barbosa-Povoa, A.P.; Novais, A.Q. An optimization model for the design of a capacitated multi-product reverse logistics network with uncertainty. Eur. J. Oper. Res. 2007, 179, 1063–1077.
  37. Salema, M.I.G.; Barbosa-Povoa, A.P.; Novais, A.Q. Simultaneous design and planning of supply chains with reverse flows: A generic modelling framework. Eur. J. Oper. Res. 2010, 203, 336–349.
  38. Cardoso, S.R.; Barbosa-Póvoa, A.P.F.D.; Relvas, S. Design and planning of supply chains with integration of reverse logistics activities under demand uncertainty. Eur. J. Oper. Res. 2013, 226, 436–451.
  39. Cardoso, S.R.; Barbosa-Póvoa, A.P.; Relvas, S.; Novais, A.Q. Resilience metrics in the assessment of complex supply-chains performance operating under demand uncertainty. Omega 2015, 56, 53–73.
  40. Paksoy, T.; Bektaş, T.; Özceylan, E. Operational and environmental performance measures in a multi-product closed-loop supply chain. Transp. Res. Part E Logist. Transp. Rev. 2011, 47, 532–546.
  41. Mota, B.; Gomes, M.I.; Carvalho, A.; Barbosa-Povoa, A.P. Towards supply chain sustainability: Economic, environmental and social design and planning. J. Clean. Prod. 2015, 105, 14–27.
  42. Gao, X. A novel reverse logistics network design considering multi-level investments for facility reconstruction with environmental considerations. Sustainability 2019, 11, 2710.
  43. Cao, S.; Liao, W.; Huang, Y. Heterogeneous fleet recyclables collection routing optimization in a two-echelon collaborative reverse logistics network from circular economic and environmental perspective. Sci. Total Environ. 2021, 758, 144062.
  44. Richnák, P.; Gubová, K. Green and reverse logistics in conditions of sustainable development in enterprises in Slovakia. Sustainability 2021, 13, 581.
  45. Chen, Z.-S.; Zhang, X.; Govindan, K.; Wang, X.-J.; Chim, K.-S. Third-party reverse logistics provider selection: A computational semantic analysis-based multi-perspective multi-attribute decision-making approach. Expert Syst. Appl. 2021, 166, 114051.
  46. Santana, J.C.C.; Guerhardt, F.; Franzini, C.E.; Ho, L.L.; Ribeiro, S.E.R., Jr.; Cânovas, G.; Yamamura, C.L.K.; Vanalle, R.M.; Berssaneti, F.T. Refurbishing and recycling of cell phones as a sustainable process of reverse logistics: A case study in Brazil. J. Clean. Prod. 2021, 283, 124585.
  47. Mishra, A.R.; Rani, P.; Pandey, K. Fermatean fuzzy CRITIC-EDAS approach for the selection of sustainable third-party reverse logistics providers using improved generalized score function. J. Ambient Intell. Hum. Comput. 2022, 13, 295–311.
  48. Chen, C.-M.; Xie, W.-C.; Li, L.-L.; Fan, S.-S.; Jiang, W.-B. The Research on Logistics Vehicle Path Optimization of Improved Ant Colony Algorithm. Adv. Sci. Lett. 2012, 11, 493–497.
  49. Foroutan, R.A.; Rezaeian, J.; Mahdavi, I. Green vehicle routing and scheduling problem with heterogeneous fleet including reverse logistics in the form of collecting returned goods. Appl. Soft Comput. 2020, 94, 106462.
  50. Chaabane, A.; Montecinos, J.; Ouhimmou, M.; Khabou, A. Vehicle routing problem for reverse logistics of End-of-Life Vehicles (ELVs). Waste Manag. 2021, 120, 209–220.
  51. Desrosiers, J.; Lübbecke, M.E. Branch-price-and-cut algorithms. In Encyclopedia of Operations Research and Management Science; John Wiley & Sons: Chichester, UK, 2011; pp. 109–131.
  52. Xu, D.; Li, K.; Zheng, P.; Tian, Q. Multi-parking, multi-vehicle, multi-category supply and demand unmatched and arbitrarily splittable delivery vehicle routing problem optimization. J. Manag. 2020, 17, 1086–1095.
  53. Fan, H.; Liu, H.; Liu, P.; Ren, X. Optimization of the simultaneous distribution and collection path of irregular vehicles with fuzzy collection demand. Control Theory Appl. 2020, 1, 14.
  54. Guo, F.; Yang, J.; Yang, C. Research on path optimization and charging strategy of multi-model electric vehicles considering differentiated service time. Chin. Manag. Sci. 2019, 27, 118–128.
  55. Zhang, M.; Pratap, S.; Zhao, Z.; Prajapati, D.; Huang, G.Q. Forward and reverse logistics vehicle routing problems with time horizons in B2C e-commerce logistics. Int. J. Prod. Res. 2021, 59, 6291–6310.
  56. Dethloff, J. Vehicle routing and reverse logistics: The vehicle routing problem with simultaneous delivery and pick-up. OR-Spektrum 2001, 23, 79–96.
  57. Masson, R.; Ropke, S.; Lehuédé, F.; Péton, O. A branch-and-cut-and-price approach for the pickup and delivery problem with shuttle routes. Eur. J. Oper. Res. 2014, 236, 849–862.
  58. Nagy, G.; Wassan, N.A.; Speranza, M.G.; Archetti, C. The vehicle routing problem with divisible deliveries and pickups. Transp. Sci. 2015, 49, 271–294.
  59. Ghilas, V.; Demir, E.; Van Woensel, T. An adaptive large neighborhood search heuristic for the pickup and delivery problem with time windows and scheduled lines. Comput. Oper. Res. 2016, 72, 12–30.
  60. Gschwind, T.; Irnich, S.; Rothenbächer, A.K.; Tilk, C. Bidirectional labeling in column-generation algorithms for pickup-and-delivery problems. Eur. J. Oper. Res. 2018, 266, 521–530.
  61. Goeke, D. Granular tabu search for the pickup and delivery problem with time windows and electric vehicles. Eur. J. Oper. Res. 2019, 278, 821–836.
  62. Wolfinger, D. A large neighborhood search for the pickup and delivery problem with time windows, split loads and transshipments. Comput. Oper. Res. 2021, 126, 105110.
  63. Haddad, M.N.; Martinelli, R.; Vidal, T.; Ochi, L.S.; Martins, S.; Jamilson, M.; Souza, J.F.M.; Hartl, R. Large neighborhood-based metaheuristic and branch-and-price for the pickup and delivery problem with split loads. Eur. J. Oper. Res. 2018, 270, 1014–1027.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Mathematics
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Yaping Ren
,
Xinyu Lu
,
Hongfei Guo
,
Zhaokang Xie
,
Haoyang Zhang
,
Chaoyong Zhang
View Times: 615
Revisions: 2 times (View History)
Update Date: 13 Jan 2023
Table of Contents
    1000/1000
    Hot Most Recent
    ScholarVision Creations
    Feedback