Reverse logistics (RL) and remanufacturing are the two main processes for end-of-life (EOL) products’ recovery, aiming to maximize resource utilization by means of collecting, disassembling, refurbishing, and reassembling to grant the EOL products the same quality and functionality as new products. In order to improve the efficiency of product recovery, it is vital to solve the combinatorial optimization problems (COPs) involved effectively; therefore, scholars have conducted much research on them.

The concept of RL was put forward by Stock [1] in 1992, whose essence was to transfer EOL products from the consumer to the producer for processing. The COPs in RL include facility location and the vehicle-routing problem (VRP). The facility location is to build an appropriate network structure to determine the location of various facilities, such as collection centers, remanufacturing centers, distribution centers, etc. The VRP is to formulate a specific transportation plan to transport EOL products to the above facilities, including the driving path, number of vehicles, types of vehicles, etc. There are some reviews about the facility location and VRP in RL ^[2][3][4][5][2,3,4,5].

However, only the transportation process of RL cannot truly realize the reuse of resources; remanufacturing is the key to achieve sustainable development [6]. Remanufacturing is a process to recover EOL products to the same state as new products through inspection, disassembly, cleaning, maintenance, replacement, reassembly, etc. [7]. The COPs involved include disassembly sequence planning (DSP), disassembly-line-balancing problem (DLBP), disassembly scheduling, production scheduling, reassembly, etc. There are also some reviews about each of the COPs in remanufacturing ^{[8][9][10][11]}[8,9,10,11].

2. Facility Location and VRP in RL

Before remanufacturing EOL products, collecting them from users is the first step, which is essentially a process of RL. To perform this efficiently, it is necessary to properly plan the location of various facilities and products’ flow routes. Specifically, companies need to choose how to collect EOL products from users and transport them to collection centers, where to inspect EOL products, where to remanufacture EOL products to make them available for resale, and how to sell remanufactured products to potential users [12]. That is to solve the problem of facility location and the VRP in RL.

2.1. Facility Location in RL

Generally, the facility location determines the location of the collection center, remanufacturing center, distributing center, and so on to minimize the logistics costs. Scholars have designed different network structures based on these facilities, which can be summarized as three types. This section will analyze the three kinds of network structures from the perspective of mathematical models, including: general network structure, closed-loop network structure, and hybrid network structure.

2.1.1. General Network Structure

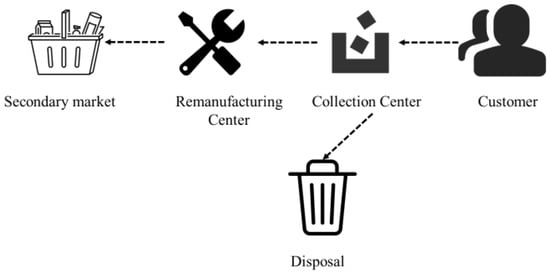
The general network structure consists of four parts: consumers, collection centers, remanufacturing centers, and secondary markets, as shown in Figure 1. The collection center collects EOL products from consumers, inspects and disassembles the products, and then, according to the value of the components, chooses to discard or remanufacture; finally, the remanufactured finished products flow back to the market for sale. It is worth noting that in this network structure, remanufactured products are usually different from new products and mainly flow to the second-hand market. It can be seen from Table 1 2 that most researchers choose the single-objective mixed-integer linear programming (MILP) model when establishing the mathematical model of the general network structure. Two papers established the mixed-integer nonlinear programming model (MILNP) ^[13][14][13,14], and they were single-objective optimization to maximize the total profit or minimize the total cost ^{[14][15][16][17][18][19][20]}[14,15,16,17,18,19,20]. However, while minimizing the total cost, Roghanian and Pazhoheshfar [21] considered the uncertainty of capacity, demand, and product quantity in RL parameters, so they proposed a probabilistic mixed-integer linear programming model (P-MILP) and converted it into an equivalent deterministic model when solving. Tari and Alumur [22] considered the fairness between different companies and the problem of providing a stable product flow for each company while minimizing the total cost, thus establishing multi-objective mixed-integer linear programming (M-MILP). In addition to minimizing the total cost and maximizing the total profit, the main purpose of establishing the mathematical model is to find out the location, capacity, and quantity of the core facilities, such as the collection center and the remanufacturing center that need to be opened in the RL network. Sasikumar et al. [13] provided decisions related to the number and location of facilities to be opened and the allocation of corresponding product flows through the establishment of MILP. Roghanian and Pazhoheshfar [21] proposed a multi-product, multi-stage RL network problem. It was not only necessary to determine the subset of disassembly centers and machining centers to be opened, but also necessary to determine the transportation strategy to meet the needs of manufacturing centers and recycling centers, with the minimum fixed opening cost and total transportation cost. Alshamsi and Diabat [16] also introduced important transportation considerations by providing options for using internal fleets and outsourcing options. Liao [14] introduced a modular remanufacturing process and emission reduction; two papers ^[14][16][14,16] also considered the carbon footprint while determining the location of factories (inspection/remanufacturing), the transportation of cores/remanufactured products between factories, and the route of vehicles between factories.

2.1.2. Closed-Loop Network Structure

To protect the environment, many countries expand producer responsibility through legislation. Driven by economic benefits, many manufacturers began to integrate RL [23], thus evolving a closed-loop network structure (CLNS), as shown in Figure 2. The CLNS integrates forward logistics and reverse logistics, producing huge economic and environmental benefits, and is the most widely studied network structure by scholars. In the CLNS, manufacturers obtain raw materials from suppliers, and the products manufactured are sold to customers through distributors. The products used by customers are collected by the collection center and selectively sent to the remanufacturing center. After remanufacturing, they return to forward logistics. In the CLNS, the terminals of forward logistics and reverse logistics are the same customer group. Table 23 and Table 34 are, respectively, the previous mathematical model research on CLNS and the corresponding abbreviations of terms. In paper [24], the environmental problems are integrated into an integer CLNS model, and a genetic algorithm based on the spanning tree structure is proposed to solve the NP-hard problem. Pishvaee et al. [25] also established a multi-objective fuzzy mathematical model to design the environmental protection supply chain. They used life cycle assessment to quantify the environmental impact of the network. Zohal and Soleimani [26] also regard the model as a green CLNS according to the CO2 emissions of the gold industry. As shown in Table 23, most scholars are studying how to use metaheuristics and heuristic algorithms to solve the model. Devika et al. [27] proposed six different mixed metaheuristics to solve the sustainable CLNS problem they developed. In paper [28], a CLNS decision model under uncertainty was proposed, and the imperialist competitive algorithm, particle swarm optimization, and genetic algorithm were used to solve the large-scale NP-hard model developed by them. In another study, Fard et al. [29] considered the three-level decision model to express their forward/reverse supply chain network design problem, and adopted a variety of metaheuristic algorithms, including tabu search, variable neighborhood search, particle swarm optimization, water wave optimization, and Keshtel algorithm. The results show that the metaheuristic algorithm is an effective method to solve the model in practice.

2.1.3. Hybrid Network Structure

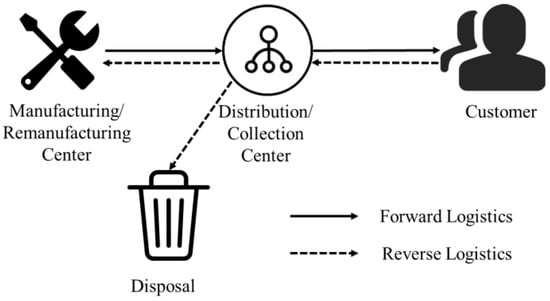
Some scholars have put forward the concept of hybrid facilities, that is, the merger of a manufacturing center and remanufacturing center, and the merger of a distribution center and collection center, as shown in Figure 3, thus representing integrated forward and reverse logistics [34]. Due to the existence of mixed facilities, RL can use the nodes of forward logistics to optimize its design, thereby effectively reducing or eliminating the cost of building new RL networks. Therefore, in recent years, it has also become a research hotspot of scholars. In this growing research field, the number of literature sources is growing rapidly. Fleischmann et al.’s pioneering work in hybrid network structure modeling studied the impact of product recycling on the design of a logistics network [35]. The study argued that the impact of product recycling depended heavily on the environment. In some cases, it may be feasible to integrate this activity into the existing logistics structure, while in other cases, it may be necessary to redesign the logistics network in an overall manner. Since this researchtudy, Salma et al. [36] incorporated capacity constraints, demand uncertainty, and returns into the multi-product planning based on this model. Later, they integrated strategic and tactical decisions by considering two inter-related time scales: at the strategic level, they gave a discretization of the time range, which must meet the needs and reporting values; at the tactical level, more detailed planning was allowed to achieve this goal [37]. Cardoso et al. [38] analyzed the integration of RL activities under demand uncertainty, took the maximum expected net present value as the objective function, and made decision variables for facility size and location, process installation, forward and reverse logistics, and inventory level. Later, the author expanded this work to solve the uncertainty and characterize the elastic closed-loop network structure [39]. Subsequently, environmental and social sustainability issues began to be considered. Paksoy et al. [40] analyzed the supply plan and considered the emission cost (total cost minimization) and the profit maximization of the recycled products in the economic objective function. Mota et al. [41] considered the sustainability of the economy, environment, and society. They proposed a mathematical model with the minimization of the total cost of the network structure as the economic objective function; the minimization of the life cycle assessment index ReCipe as the environmental objective function; and the location of the network structure activities in underdeveloped areas as the social objective function. Gao et al. [42], based on the existing forward logistics network, proposed a double-objective stochastic integer programming model aiming at economic and environmental benefits, which aimed to support production, remanufacturing, and waste activities by addressing the uncertainty factors of new product demand and the return volume of old products in the customer area.

2.2. VRP in RL

After locating critical facilities, the next question is how to reversely transport EOL products, that is, the vehicle-routing problem in RL. The VRP in RL refers to how to arrange vehicle types, quantities, capacities, routes, etc., to collect waste products from customers, to achieve the goal of the minimum cost or the shortest route. Collection is the starting point of EOL product recovery, so scholars have carried out much research to improve the efficiency of this link. The VRP in RL can be described as: a certain number of customers must use a certain number of fleets with limited capacity, which are usually assumed to be the same. The vehicles are stationed in a central parking lot and return after collecting waste products from customers according to the route requirements. Cao et al. [43] used RL to reuse the Internet of Things through identifying the resources required for road infrastructure, and modeled RL to transfer the Internet of Things from a tailings dam to a processing plant, and then to a road construction site. For minimizing the total cost, Richnák and Gubová [44] established a heterogeneous-fleet electric-vehicle path-recovery time window model considering vehicle load constraints. The type of vehicle limited the weight of recyclable waste and the time limit allowed by the customer. Chen et al. [45] proposed a nonlinear programming model including the number of second-hand products and reprocessed products. For both types of requirements, analysis and insight were provided in the form of a complete strategy consisting of different scenarios that allow optimal decisions to be made under a variety of conditions. Through sensitivity analysis, numerical examples supplemented the understanding of the model. Santana et al. [46] considered the risks in the e-waste recycling process and modeled the reverse logistics process of electrical and electronic equipment as a MILP with biological objectives under uncertainty. The cooperative alliance strategy was employed by Mishra et al. [47] to actualize the constrained capabilities of VRP in RL. The cooperative mechanism made it possible to prevent inefficient resource distribution, cut back on circular logistics, and minimize long-distance travel. In order to minimize recovery tasks, Chen et al. [48] used an improved ant colony algorithm to handle vehicle design and route optimization problems. Foroutan et al. [49] established a mixed-integer nonlinear programming model for multi-mode green vehicle routing and scheduling with the objective of minimizing operating costs and environmental costs and considering return, lead time, and delay costs. A mathematical model for the recovery of EOL cars was developed by Chaabane et al. [50] by combining the traditional VRP with the receiving and delivery problem as well as the restrictions of various vehicle kinds and time periods. The multi-vehicle routing optimization problem with time limitations has also been the subject of interest for scholars’ in-depth research. In order to meet the needs of minimizing transportation and procurement costs, the research in the literature [51] included choosing suppliers and setting up homogeneous fleets to buy various products from chosen suppliers. It also defined new branching rules, introduced new inequality families, and established the competitiveness of the new branching price-reduction method. To optimize the multi-depot production material-allocation system and research the routing problem of delivery vehicles, Xu et al. [52] took into account a variety of factors, including multiple warehouses, multiple vehicle types, multiple commodities, mismatches between customer supply and demand, and arbitrary segmentation of delivery and delivery demands. Fan et al. [53] designed a genetic variable neighborhood algorithm for multi-vehicle routing optimization problem with fuzzy set requirements by improving the adaptive search strategy. A multi-mode electric vehicle routing optimization model was developed by Guo et al. [54] taking into account the differentiating service costs under the consideration of vehicle diversity, charging strategy, person vehicle matching, and service time difference. With the improvement in logistics network and the development of e-commerce, in order to improve customer satisfaction, logistics service providers need to handle a large number of delivery orders and return orders at the same time. In this case, the joint optimization of simultaneous pickup and delivery VRP (VRPSPD) can significantly improve the utilization rate of vehicles [55]. Studies have shown that solving the problem of collecting refurbished goods in forward and reverse logistics can improve the utilization rate of refurbished products, shorten the return time, and improve customer satisfaction [55]. Dethloff [56] studied VRPSPD in order to avoid redundant handling work, considering that customers have both picking and delivery needs. They developed an insertion-based heuristics method, which can be used to construct initial feasible solutions, which can be improved by subsequent application of the local search process. A specific case of VRPSPD that allows for the decomposition of the picking and delivery needs was developed by Masson et al. [57]. This method can be used in real-world transportation systems with many of pickup trucks but few deliveries. Nagy et al. [58] proposed a VRP with separable delivery and picking, and studied the cost reduction caused by demand segmentation of simultaneous delivery and pickup. In order to optimize vehicle scheduling to satisfy freight requests, Ghilas et al. [59] created a VRPSPD with scheduling lines and took synchronization and time window limitations into account in the solution algorithm. Gschwind et al. [60] evaluated the performance of branch cut and price algorithms in VRPSPD to solve the shortest path issue under time windows and resource limitation. Goeke [61] investigated the VRPSPD of electric cars, in which the route design of electric vehicles attempted to optimize the pick-up and delivery services in metropolitan areas with a lower environmental impact. Wolfinger [62] proposed a mixed-integer programming model to develop a single warehouse VRPPD with split load, and tested the algorithm performance through extensive computing experiments through large-scale neighborhood search. Haddad et al. [63] developed a multi-warehouse VRPPD to design a sustainable picking and distribution route between multiple warehouses. The efficiency of transportation can be increased at the same time, within the limitations of vehicle capacity and time window.