1. Definition

Visualization of the ${\displaystyle \mathrm{\wp }}$-function with invariants ${\displaystyle g_2=1+i}$ and ${\displaystyle g_3=2-3i}$ in which white corresponds to a pole, black to a zero. https://handwiki.org/wiki/index.php?curid=1280544

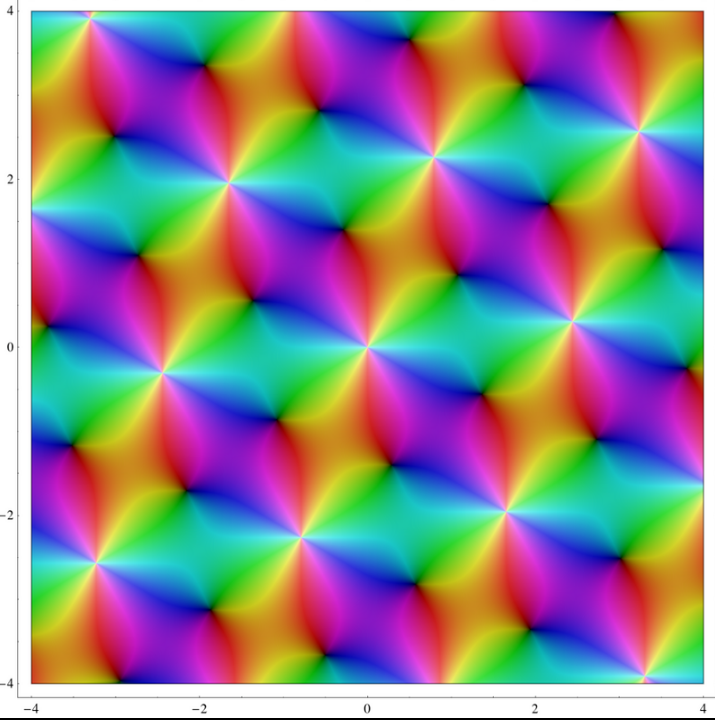
Let ${\displaystyle {\omega }_1,{\omega }_2\in \mathbb{C}}$ be two complex numbers that are linear independent over ${\displaystyle \mathbb{R}}$ and let ${\displaystyle \mathrm{\Lambda }:=\mathbb{Z}{\omega }_1+\mathbb{Z}{\omega }_2:=\{m{\omega }_1+n{\omega }_2:m,n\in \mathbb{Z}\}}$ be the lattice generated by those numbers. Then the ${\displaystyle \mathrm{\wp }}$-function is defined as follows:

$\text{Undefined control sequence weierp}$

This series converges locally uniformly absolutely in ${\displaystyle \mathbb{C}\setminus \mathrm{\Lambda }}$. Oftentimes instead of ${\displaystyle \mathrm{\wp }(z,{\omega }_1,{\omega }_2)}$ only ${\displaystyle \mathrm{\wp }(z)}$ is written.

The Weierstrass ${\displaystyle \mathrm{\wp }}$-function is constructed exactly in such a way that it has a pole of the order two at each lattice point.

Because the sum ${\displaystyle \sum _{\lambda \in \mathrm{\Lambda }}\frac{1}{(z-\lambda {)}^2}}$ alone would not converge it is necessary to add the term ${\displaystyle -\frac{1}{{\lambda }^2}}$.^[1]

It is common to use ${\displaystyle 1}$ and $\text{Undefined control sequence operatorname}$ as generators of the lattice. Multiplying by ${\displaystyle \frac{1}{{\omega }_1}}$ maps the lattice ${\displaystyle \mathbb{Z}{\omega }_1+\mathbb{Z}{\omega }_2}$ isomorphically onto the lattice ${\displaystyle \mathbb{Z}+\mathbb{Z}\tau }$ with ${\displaystyle \tau =\frac{{\omega }_2}{{\omega }_1}}$. By possibly substituting ${\displaystyle \tau }$ by ${\displaystyle -\tau }$ it can be assumed that ${\displaystyle \tau \in \mathbb{H}}$. One sets ${\displaystyle \mathrm{\wp }(z,\tau ):=\mathrm{\wp }(z,1,\tau )}$.

2. Motivation

A cubic of the form ${\displaystyle C_{g_2,g_3}^{\mathbb{C}}=\{(x,y)\in {\mathbb{C}}^2:y^2=4x^3-g_{2}x+g_3\}}$, where ${\displaystyle g_2,g_3\in \mathbb{C}}$ are complex numbers with ${\displaystyle g_2^3-27g_3^2\ne 0}$, can not be rationally parameterized.^[2] Yet one still wants to find a way to parameterize it.

For the quadric ${\displaystyle K=\{(x,y)\in {\mathbb{R}}^2:x^2+y^2=1\}}$, the unit circle, there exists a (non-rational) parameterization using the sine function and its derivative the cosine function:

${\displaystyle \psi :\mathbb{R}/2\pi \mathbb{Z}\to K,t\mapsto (\sin (t),\cos (t))}$.

Because of the periodicity of the sine and cosine ${\displaystyle \mathbb{R}/2\pi \mathbb{Z}}$ is chosen to be the domain, so the function is bijective.

In a similar way one can get a parameterization of ${\displaystyle C_{g_2,g_3}^{\mathbb{C}}}$ by means of the doubly periodic ${\displaystyle \mathrm{\wp }}$-function (see in the section "Relation to ellitpic curves"). This parameterization has the domain ${\displaystyle \mathbb{C}/\mathrm{\Lambda }}$, which is topologically equivalent to a torus.^[3]

There is another analogy to the trigonometric functions. Consider the integral function

${\displaystyle a(x)={\int }_0^x\frac{dy}{\sqrt{(1-y^2)}}}$.

It can be simplified by substituting ${\displaystyle y=\sin (t)}$ and ${\displaystyle s=\arcsin (x)}$:

${\displaystyle a(x)={\int }_0^{s}dt=s=\arcsin (x)}$.

That means ${\displaystyle a^{-1}(x)=\sin (x)}$. So the sine function is an inverse function of an integral function.^[4]

Elliptic functions are also inverse functions of integral functions, namely of elliptic integrals. In particular the ${\displaystyle \mathrm{\wp }}$-function is obtained in the following way:

Let

$\text{Undefined control sequence infin}$.

Then ${\displaystyle u^{-1}}$ can be extended to the complex plane and this extension equals the ${\displaystyle \mathrm{\wp }}$-function.^[5]

3. Properties

• ℘ is an even function. That means ${\displaystyle \mathrm{\wp }(z)=\mathrm{\wp }(-z)}$ for all ${\displaystyle z\in \mathbb{C}\setminus \mathrm{\Lambda }}$, which can be seen in the following way:

$\text{Undefined control sequence weierp}$

The second last equality holds because ${\displaystyle \{-\lambda :\lambda \in \mathrm{\Lambda }\}=\mathrm{\Lambda }}$. Since the sum converges absolutely this rearrangement does not change the limit.

• ℘ is meromorphic and its derivative is^[6]

${\displaystyle {\mathrm{\wp }}^{\prime }(z)=-2\sum _{\lambda \in \mathrm{\Lambda }}\frac{1}{(z-\lambda {)}^3}}$.

• ${\displaystyle \mathrm{\wp }}$ and ${\displaystyle {\mathrm{\wp }}^{\prime }}$ are doubly periodic with the periods ${\displaystyle {\omega }_1}$und ${\displaystyle {\omega }_2}$.^[6] This means:

${\displaystyle \mathrm{\wp }(z+{\omega }_1)=\mathrm{\wp }(z)=\mathrm{\wp }(z+{\omega }_2)}$ and ${\displaystyle {\mathrm{\wp }}^{\prime }(z+{\omega }_1)={\mathrm{\wp }}^{\prime }(z)={\mathrm{\wp }}^{\prime }(z+{\omega }_2)}$.

It follows that ${\displaystyle \mathrm{\wp }(z+\lambda )=\mathrm{\wp }(z)}$ and ${\displaystyle {\mathrm{\wp }}^{\prime }(z+\lambda )={\mathrm{\wp }}^{\prime }(z)}$ for all ${\displaystyle \lambda \in \mathrm{\Lambda }}$. Functions which are meromorphic and doubly periodic are also called elliptic functions.

4. Laurent Expansion

Let ${\displaystyle r:=min\{|\lambda |:0\ne \lambda \in \mathrm{\Lambda }\}}$. Then for ${\displaystyle 0<|z|<r}$ the ${\displaystyle \mathrm{\wp }}$-function has the following Laurent expansion

$\text{Undefined control sequence infin}$

where

${\displaystyle G_n=\sum _{0\ne \lambda \in \mathrm{\Lambda }}{\lambda }^{-n}}$ for ${\displaystyle n\ge 3}$ are so called Eisenstein series.^[6]

5. Differential Equation

Set ${\displaystyle g_2=60G_4}$ and ${\displaystyle g_3=140G_6}$. Then the ${\displaystyle \mathrm{\wp }}$-function satisfies the differential equation^[6]

${\displaystyle {\mathrm{\wp }}^{\prime 2}(z)=4{\mathrm{\wp }}^3(z)-g_2\mathrm{\wp }(z)-g_3}$.

This relation can be verified by forming a linear combination of powers of ${\displaystyle \mathrm{\wp }}$ and ${\displaystyle {\mathrm{\wp }}^{\prime }}$ to eliminate the pole at ${\displaystyle z=0}$. This yields an entire elliptic function that has to be constant by Liouville's theorem .^[6]

6. Invariants

The real part of the invariant g₃ as a function of the nome q on the unit disk. https://handwiki.org/wiki/index.php?curid=1389931

The imaginary part of the invariant g₃ as a function of the nome q on the unit disk. https://handwiki.org/wiki/index.php?curid=1178918

The coefficients of the above differential equation g₂ and g₃ are known as the invariants. Because they depent on the lattice ${\displaystyle \mathrm{\Lambda }}$ they can be viewed as functions in ${\displaystyle {\omega }_1}$and ${\displaystyle {\omega }_2}$.

The series expansion suggests that g₂ and g₃ are homogeneous functions of degree −4 and −6. That is^[7]

${\displaystyle g_2(\lambda {\omega }_1,\lambda {\omega }_2)={\lambda }^{-4}{g}_2({\omega }_1,{\omega }_2)}$

${\displaystyle g_3(\lambda {\omega }_1,\lambda {\omega }_2)={\lambda }^{-6}{g}_3({\omega }_1,{\omega }_2)}$ for ${\displaystyle \lambda \ne 0}$.

If ${\displaystyle {\omega }_1}$and ${\displaystyle {\omega }_2}$ are chosen in such a way that $\text{Undefined control sequence operatorname}$ g₂ and g₃ can be interpreted as functions on the upper half-plane $\text{Undefined control sequence operatorname}$.

Let ${\displaystyle \tau =\frac{{\omega }_2}{{\omega }_1}}$. One has:^[8]

${\displaystyle g_2(1,\tau )={\omega }_1^4{g}_2({\omega }_1,{\omega }_2)}$,

${\displaystyle g_3(1,\tau )={\omega }_1^6{g}_3({\omega }_1,{\omega }_2)}$.

That means g₂ and g₃ are only scaled by doing this. Set

${\displaystyle g_2(\tau ):=g_2(1,\tau )}$, ${\displaystyle g_3(\tau ):=g_3(1,\tau )}$.

As functions of ${\displaystyle \tau \in \mathbb{H}}$ ${\displaystyle g_2,g_3}$ are so called modular forms.

The Fourier series for ${\displaystyle g_2}$ and ${\displaystyle g_3}$ are given as follows:^[9]

${\displaystyle g_2(\tau )=\frac{4}{3}{\pi }^4[1+240\sum _{k=1}^{\mathrm{\infty }}{\sigma }_3(k)q^{2k}]}$

${\displaystyle g_3(\tau )=\frac{8}{27}{\pi }^6[1-504\sum _{k=1}^{\mathrm{\infty }}{\sigma }_5(k)q^{2k}]}$

where ${\displaystyle {\sigma }_a(k):=\sum _{d\mid k}{d}^{\alpha }}$ is the divisor function and ${\displaystyle q:=\exp (i\pi \tau )}$.

7. Modular Discriminant

The real part of the discriminant as a function of the nome q on the unit disk.

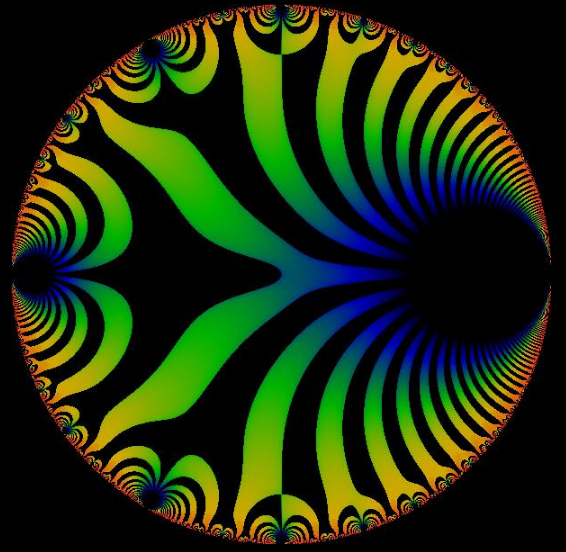
The modular discriminant Δ is defined as the discriminant of the polynomial at right-hand side of the above differential equation:

${\displaystyle \mathrm{\Delta }=g_2^3-27g_3^2.}$

The discriminant is a modular form of weight 12. That is, under the action of the modular group, it transforms as

${\displaystyle \mathrm{\Delta }\left(\frac{a\tau +b}{c\tau +d}\right)={(c\tau +d)}^{12}\mathrm{\Delta }(\tau )}$

where ${\displaystyle a,b,d,c\in \mathbb{Z}}$ with ad − bc = 1.^[10]

Note that ${\displaystyle \mathrm{\Delta }=(2\pi {)}^{12}{\eta }^{24}}$ where ${\displaystyle \eta }$ is the Dedekind eta function.^[11]

For the Fourier coefficients of ${\displaystyle \mathrm{\Delta }}$, see Ramanujan tau function.

8. The Constants e₁, e₂ and e₃

${\displaystyle e_1}$, ${\displaystyle e_2}$ and ${\displaystyle e_3}$ are usually used to denote the values of the ${\displaystyle \mathrm{\wp }}$-function at the half-periods.

${\displaystyle e_1\equiv \mathrm{\wp }\left(\frac{{\omega }_1}{2}\right)}$

${\displaystyle e_2\equiv \mathrm{\wp }\left(\frac{{\omega }_2}{2}\right)}$

${\displaystyle e_3\equiv \mathrm{\wp }\left(\frac{{\omega }_1+{\omega }_2}{2}\right)}$

They are pairwise distinct and only depend on the lattice ${\displaystyle \mathrm{\Lambda }}$ and not on its generators.^[12]

${\displaystyle e_1}$, ${\displaystyle e_2}$ and ${\displaystyle e_3}$ are the roots of the cubic polynomial ${\displaystyle 4\mathrm{\wp }(z{)}^3-g_2\mathrm{\wp }(z)-g_3}$ and are related by the equation:

${\displaystyle e_1+e_2+e_3=0}$.

Because those roots are distinct the discriminant ${\displaystyle \mathrm{\Delta }}$ does not vanish on the upper half plane.^[13] Now we can rewrite the differential equation:

${\displaystyle {\mathrm{\wp }}^{\prime 2}(z)=4(\mathrm{\wp }(z)-e_1)(\mathrm{\wp }(z)-e_2)(\mathrm{\wp }(z)-e_3)}$.

That means the half-periods are zeros of ${\displaystyle {\mathrm{\wp }}^{\prime }}$.

The invariants ${\displaystyle g_2}$ and ${\displaystyle g_3}$ can be expressed in terms of these constants in the following way:^[14]

${\displaystyle g_2=-4(e_1{e}_2+e_1{e}_3+e_2{e}_3)}$

${\displaystyle g_3=4e_1{e}_2{e}_3}$

9. Relation to Elliptic Curves

Consider the projective cubic curve

$\text{Undefined control sequence infin}$.

For this cubic, also called Weierstrass cubic, there exists no rational parameterization, if ${\displaystyle \mathrm{\Delta }\ne 0}$.^[2] In this case it is also called an elliptic curve. Nevertheless there is a parameterization that uses the ${\displaystyle \mathrm{\wp }}$-function and its derivative ${\displaystyle {\mathrm{\wp }}^{\prime }}$:^[15]

$\text{Unknown environment 'cases'}$

Now the map ${\displaystyle \phi }$ is bijective and parameterizes the elliptic curve ${\displaystyle {\overline{C}}_{g_2,g_3}^{\mathbb{C}}}$.

${\displaystyle \mathbb{C}/\mathrm{\Lambda }}$ is an abelian group and a topological space, equipped with the quotient topology.

It can be shown that every Weierstrass cubic is given in such a way. That is to say that for every pair ${\displaystyle g_2,g_3\in \mathbb{C}}$ with ${\displaystyle \mathrm{\Delta }=g_2^3-27g_3^2\ne 0}$ there exists a lattice ${\displaystyle \mathbb{Z}{\omega }_1+\mathbb{Z}{\omega }_2}$, such that

${\displaystyle g_2=g_2({\omega }_1,{\omega }_2)}$ and ${\displaystyle g_3=g_3({\omega }_1,{\omega }_2)}$.^[16]

The statement that elliptic curves over ${\displaystyle \mathbb{Q}}$ can be parameterized over ${\displaystyle \mathbb{Q}}$, is known as the modularity theorem. This is an important theorem in number theory. It was part of Andrew Wiles' proof (1995) of Fermat's Last Theorem.

10. Addition Theorems

Let ${\displaystyle z,w\in \mathbb{C}}$, so that ${\displaystyle z,w,z+w,z-w\notin \mathrm{\Lambda }}$. Then one has:^[17]

${\displaystyle \mathrm{\wp }(z+w)=\frac{1}{4}{\left[\frac{{\mathrm{\wp }}^{\prime }(z)-{\mathrm{\wp }}^{\prime }(w)}{\mathrm{\wp }(z)-\mathrm{\wp }(w)}\right]}^2-\mathrm{\wp }(z)-\mathrm{\wp }(w)}$.

As well as the duplication formula:^[17]

${\displaystyle \mathrm{\wp }(2z)=\frac{1}{4}{\left[\frac{{\mathrm{\wp }}^{″}(z)}{{\mathrm{\wp }}^{\prime }(z)}\right]}^2-2\mathrm{\wp }(z)}$.

These formulas also have a geometric interpretation, if one looks at the elliptic curve ${\displaystyle {\overline{C}}_{g_2,g_3}^{\mathbb{C}}}$ together with the mapping ${\displaystyle \phi :\mathbb{C}/\mathrm{\Lambda }\to {\overline{C}}_{g_2,g_3}^{\mathbb{C}}}$ as in the previous section.

The group structure of ${\displaystyle (\mathbb{C}/\mathrm{\Lambda },+)}$ translates to the curve ${\displaystyle {\overline{C}}_{g_2,g_3}^{\mathbb{C}}}$and can be geometrically interpreted there:

The sum of three pairwise different points ${\displaystyle a,b,c\in {\overline{C}}_{g_2,g_3}^{\mathbb{C}}}$is zero if and only if they lie on the same line in ${\displaystyle {\mathbb{P}}_{\mathbb{C}}^2}$.^[18]

This is equivalent to:

${\displaystyle det\left(\begin{array}{rrr}1& \mathrm{\wp }(u+v)& -{\mathrm{\wp }}^{\prime }(u+v)\\ 1& \mathrm{\wp }(v)& {\mathrm{\wp }}^{\prime }(v)\\ 1& \mathrm{\wp }(u)& {\mathrm{\wp }}^{\prime }(u)\end{array}\right)=0}$,

where ${\displaystyle \mathrm{\wp }(u)=a}$, ${\displaystyle \mathrm{\wp }(v)=b}$ and ${\displaystyle u,v\notin \mathrm{\Lambda }}$.^[19]

11. Relation to Jacobi's Elliptic Functions

For numerical work, it is often convenient to calculate the Weierstrass elliptic function in terms of Jacobi's elliptic functions.

The basic relations are:^[20]

$\text{Undefined control sequence operatorname}$

where ${\displaystyle e_1,e_2}$and ${\displaystyle e_3}$ are the three roots described above and where the modulus k of the Jacobi functions equals

${\displaystyle k=\sqrt{\frac{e_2-e_3}{e_1-e_3}}}$

and their argument w equals

${\displaystyle w=z\sqrt{e_1-e_3}.}$

12. Typography

The Weierstrass's elliptic function is usually written with a rather special, lower case script letter ℘.^[21]

In computing, the letter ℘ is available as \wp in TeX. In Unicode the code point is U+2118 ℘ SCRIPT CAPITAL P (HTML ℘ · ℘), with the more correct alias weierstrass elliptic function.^[22] In HTML, it can be escaped as ℘.