You're using an outdated browser. Please upgrade to a modern browser for the best experience.

Submitted Successfully!
Thank you for your contribution! You can also upload a video entry or images related to this topic.
For video creation, please contact our Academic Video Service.
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | ABDULRAHMAN ABDULLAH BAHASHWAN | -- | 3833 | 2022-11-29 07:07:35 | | | |
| 2 | Amina Yu | -3 word(s) | 3830 | 2022-11-30 01:39:54 | | |
Video Upload Options
We provide professional Academic Video Service to translate complex research into visually appealing presentations. Would you like to try it?
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Bahashwan, A.A.; Ibrahim, R.B.; Omar, M.B.; Faqih, M.; Bahashwan, A.A. The Lean Blowout Prediction Techniques. Encyclopedia. Available online: https://encyclopedia.pub/entry/37013 (accessed on 15 December 2025).
Bahashwan AA, Ibrahim RB, Omar MB, Faqih M, Bahashwan AA. The Lean Blowout Prediction Techniques. Encyclopedia. Available at: https://encyclopedia.pub/entry/37013. Accessed December 15, 2025.
Bahashwan, Abdulrahman Abdullah, Rosdiazli Bin Ibrahim, Madiah Binti Omar, Mochammad Faqih, Abdulrahman Abdullah Bahashwan. "The Lean Blowout Prediction Techniques" Encyclopedia, https://encyclopedia.pub/entry/37013 (accessed December 15, 2025).
Bahashwan, A.A., Ibrahim, R.B., Omar, M.B., Faqih, M., & Bahashwan, A.A. (2022, November 29). The Lean Blowout Prediction Techniques. In Encyclopedia. https://encyclopedia.pub/entry/37013
Bahashwan, Abdulrahman Abdullah, et al. "The Lean Blowout Prediction Techniques." Encyclopedia. Web. 29 November, 2022.
Copy Citation
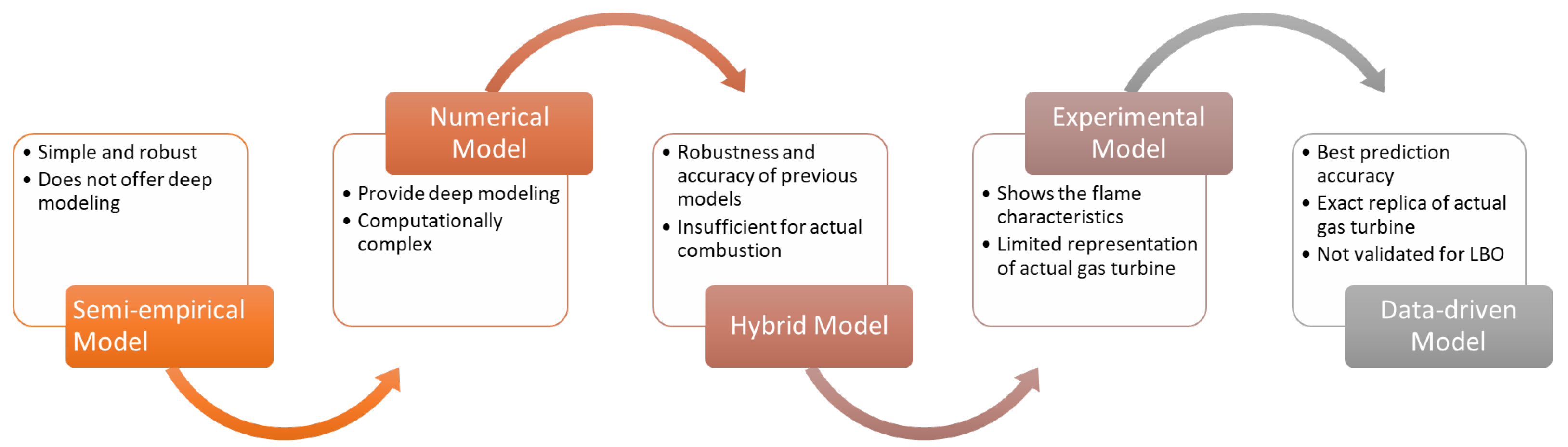
The lean blowout is the most critical issue in lean premixed gas turbine combustion. Decades of research into LBO prediction methods have yielded promising results. Predictions can be classified into five categories based on methodology: semi-empirical model, numerical simulation, hybrid, experimental, and data-driven model.
gas turbine
lean premixed combustor
lean blowout
prediction technique
data-driven
1. The Semi-Empirical Model
The combustors’ geometries are pretty complicated. Because of the high complexity, the semi-empirical model is proposed based on the physical approach to simplify the system because the physics-based model is the preferred model within the semi-empirical. In addition, the semi-empirical model could help provide a good estimation of the gas turbine performance and can be used to improve the LBO limits at the design stages of the LPM combustors. Because of this simultaneous complexity, it is recommended that a semi-empirical model be used to simplify the system [1].
The swirl-stabilized combustor is the most common form of the gas turbine. The LBO mechanism and prediction techniques for such combustors have been extensively explored during the last decades. One of the most widely used approaches for predicting the lean blowout gas turbine is the the semi-empirical-based model. Since the semi-empirical approach was developed earlier, it has gone through a lengthy study process and has been progressively changed and enhanced to ensure its suitability for engineering applications. The model is mainly used for LBO limits prediction in the gas turbine. It was an essential tool for designing a lean premixed combustor with better LBO limits. The semi-empirical approach can be divided into two categories: the first is the characteristic time (CT) and the second is the perfect stirred reactor (PSR).
The CT model is based on the Damkohler (Da) number, and it was was pioneered by Zukoski and Marble [2], who made a breakthrough in the semi-empirical models in 1955. The authors used the ignition delay time of the fuel/air mixes as an equivalent to the time required for shear layer mixing. In another word, The LBO would occur when the ignition delay time is longer than the particle time spent in the shear layer. On the opposite side, the combustion is stable when the ignition delay time is shorter. Therefore, the indication of LBO is when both times are equal. The equation can be written as follows
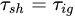
where τsh and τig are the particle time spent in a shear layer and the ignition delay time, respectively. Such a simple equation was beneficial in the early stages of LPM combustion design to predict the LBO limits in terms of determining the best recirculating zone length and the stream velocity, as the equation can be further written as follows

where Lrz and Vs are the length of the recirculation zone and the steam velocity. Because of the simplicity of the model, it needed further development to predict the LBO limit accurately. Later, Plee and Mellor [3] improved the characteristic time model’s prediction formula of Zukoaki and Marble, and they added droplet evaporation rates to the preceding model and successfully validated the model on three types of combustors [4][5][6][7]. The equation of Plee and Mellor can be expressed as follows
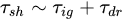
where Tdr is the droplet evaporation rate. However, the performance of the model was not optimum.
On the other hand, Longwell et al. [8] in 1953 hypothesized that the recirculation zone behind a bluff body might be idealized as a Perfect Stirred Reactor (PSR), with the burning zone being the PSR. The PSR model became a central tenet in the research of the LBO semi-empirical models. The authors suggested that when the heat loss in the recirculation zone and the heat released are equal, LBO will occur. Additionally, they observed that the pressure of the recirculation zone is proportional to the stability of LBO velocity.
Later, Lefebvre [9][10], one of the pioneers of the semi-empirical model, developed a model and advanced the prediction formula and expression based on Longwells’s work to make it capable of predicting LBO limits in the swirl-stabilized combustors. According to Lefebvre’s LBO model, the LBO limitations are determined by combustor geometries, operation conditions, and fuel characteristics. The main assumptions of Lefebvre’s model are that the whole inlet air flow is involved in the fuel mixing and combustion at the LBO, and secondly, the turbulent flame filled the whole combustor at LBO, as shown in the physical model of Lefebvre’s expression. The model was validated on eight different combustors with uncertainties of ±30% [11].
Afterward, numerous works to improve the Lefebvre model have been suggested, as Lefebvre’s formula uses a constant to represent the combustor configurations of the upstream dilution holes, which limits the model’s applicability in different variations of combustors. Therefore, a study used a formula to replace the constant value in Lefebvre’s model, as documented by Ateshkadi et al. [12], and they included a temperature-based parameter collected from their experimental results. However, Mongia et al. [13] revealed that none of the existing models can be used for modern combustion and suggested that the focus should be on the flame volume rather than the combustion volume to improve Lefebvre’s model further. Later, Mongia et al. [14] used a data reduction to evaluate the test data in order to achieve more accurate predictions. They then optimized Lefebvre’s LBO model’s parameters and exponents to be applicable to 5 different combustors.
Furthermore, Xie et al. [15] proposed a new semi-empirical model based on Lefebvre’s model better to investigate the impact of geometrical structural factors on combustors. The authors used the concept of flame volume (FV) observations based on a visualization experiment of the flame size at different fuel/air ratios. It was noticed that the flame could not fill the whole area within the combustor liner near the LBO, and it was instead very short. Adding the FV approach has improved Lefebvre’s model. It considers the effect of the variation in primary zone configuration and the dome geometry as the FV varies depending on the combustor’s design. The main assumptions of the FV model at LBO are that the inlet airflow can be divided into two parts: the airflow involved in the combustion (dome airflow and part of the liner airflow) and the airflow in the dilution downstream, as shown in the physical model of FV LBO expression. The second assumption is that the remaining airflow enters the liner uniformly, and the airflow involved in the combustion depends on the size of the turbulent flame zone.
The flame volume approach offers a more direct link between LBO performance and flame characteristics, so increasing the modeling depth and, consequently, the prediction accuracy [16]. On the other hand, with the recent development in LPM combustion, the ultra-low NOx emission gas turbine came into existence. The geometry of the new combustor’s dome differs from the previous combustors to achieve lower NOx emission and better stability. The fuel/air inlets are divided into the main and pilot stages. Only the pilot stages operate near LBO to ensure power and flame stability. Due to the differences in the previous and the current dome configuration, the earlier models’ performance was not ideal for predicting the LBO limits. Therefore, another study was conducted by Sun et al. [17], who improved the FV model by using a novel flame volume and multi-point (FV-MP) to be used for the low NOx combustor.
Similarly, Rowen’s model is a well-known semi-empirical model that is used explicitly for heavy-duty gas turbines [18]. Rowen’s model is a simplified mathematical representation of the conventional gas turbine, as shown in the simplified block diagram. However, due to the recent development and the existance of the dry low emission (DLE) gas turbine, the model was improved by Omar et al. [19][20][21][22] by adding a pilot fuel valve based on the DLE gas turbine operational data. The improved model could produce high accuracy prediction for the gas turbine performance, and it can be used for LBO limits prediction for the new combustors.
When it comes to dealing with lean blowout limit prediction, the semi-empirical methodologies are often the most practical options due to their simplicity, robustness, and cost-effectiveness. Its primary use is in the design stage, where it assists in the investigation of the limits of the LBO and developing combustors that are more resistant to such an occurrence. Until today, the semi-empirical model is widely utilized in aero-engine lean blowout prediction but not in heavy-duty industrial gas turbines. Although this strategy is the oldest one compared to the others, and even though it has undergone many different types of development and refinement, it still has significant drawbacks. It exhibits little generalizability in a variety of combustors; therefore, the degree of uncertainty might be as high as fifty percent, particularly with regard to newly developed combustors [23]. Similarly, the lack of depth in the semi-empirical modeling substantially impacts the accuracy and inability to associate the geometric variation with the LBO events [16]. On the other hand, as was mentioned earlier, various semi-empirical models, such as Rowen’s model, show promising results in presenting the lean premixed heavy-duty gas turbines. These results are especially promising when the models are associated with a numerical simulation approach or a data-driven configuration to improve their accuracy of LBO limits predictions.
2. Numerical Simulation
The semi-empirical model provided fundamental information for the prediction of LBO limits. However, it was a simplistic approach and does not provide deeper knowledge on the matter as shown in the development process in Figure 1. Therefore, there has been an increase in the reporting of numerical prediction methods in recent years. The LBO limits are often determined using either the Large Eddy Simulation (LES) or Unsteady Reynolds-averaged Navier–Stokes (URANS) methods. In the past, LES and Direct Numerical Simulation (DNS) have been used in numerical modeling to capture the dynamic features of the flame close to the LBO. Furthermore, the flow features have been studied extensively [24]. As a result, several articles published use numerical simulations to investigate the LBO phenomena. The main strength of numerical simulation is the capacity to construct complicated flow fields, both non-reactive and reactive. Nearly all studies using numerical models have revealed that the flow field is volatile close to the LBO [25].

Figure 1. Development of LBO prediction techniques.
Although there have been many advancements in modeling techniques over the last several decades, two main frameworks have arisen depending on the degree of characterization of the underlying flow: the Reynolds-averaged Navier–Stokes (RANS) approach and the recent Large Eddy Simulation (LES) method. The RANS approach is still a popular method for LBO prediction and is preferred to the LES in some studies due to its low computational cost and complexity, due to the disregard of the time resolution, as documented by Ahmed and Yong [16]. The authors predicted the LBO using the primary zone’s flow structure. Then, the data were simulated using RANS simulation and compared with experimental data. The result showed high efficiency in predicting LBO. Later, Akhtar et al. [26] used a combination of a flame-generated-manifold (FGM) model and Reynolds-Averaged Navier–Stokes (RANS) turbulence modeling to explore a turbulent premixed single jet flame at an enhanced preheating temperature and pressure. They discovered that the flame location depended on the input velocity or turbulence and could compute LBO limits with a ±20% uncertainty compared to the experimental blowout velocity. Nevertheless, RANS is less accurate than LES and considered a non-universal approach [27].
On the other hand, the LES technique has emerged as the go-to numerical tool for combustion applications because of its efficacy in describing turbulent physical processes. In addition, the LES framework may take advantage of the exponential growth of computation speed by steadily amplifying the range of physical length and time scales that are directly resolved rather than modeled. This is where LES comes in handy as it provides a smooth transition to model-free DNS [28]. As a result, the discipline of turbulent combustion has majorly chosen the LES method, leading to impressive developments in a number of subfields [29][30]. It has been used in a number of studies, such as those of Ihme and Pitsch [31], Garmory and Mastorakos [32], Ayache et al. [33], and Hasti et al. [34], to predict the LBO successfully.
Furthermore, some studies suggested using the chemical reduction technique to reduce the computation time, especially by utilizing the FGM model with the LES model as documented by Nassini et al. [35]. The authors investigated the flame behavior and fragmentation of the flame using the FGM model based on an expanded turbulent flame closure (TFC) technique and the LES simulation. The two tested operating conditions deviated from the computed equivalence ratio by ±5% and ±10% from the experimental LBO point. Similarly, Schwagerus et al. [36] used FGM with LES simulation to reduce computation time. The authors focused on observing flame shape changes close to LBO by decreasing the fuel/air equivalence ratios Φ with constant inlet velocity. Secondly, by increasing the inlet velocity with a constant fuel/air equivalence ratios Φ, the result showed a conical flame under unstable conditions and the flame extended near LBO. The LBO occurs after reducing the equivalence ratios Φ and increasing the inlet velocity. The results of the proposed approach were very close to the experimental findings.
Additionally, other studies used the simulation method to predict the LBO away from the LES and RANS as documented by Maran et al. [37]. The authors used simulations for various intake pressures and V-gutter angles. A simplified approach was used for predicting the LBO for an afterburner combustor by using the recirculation zone’s average gas temperature (AGT). The prediction was successful and showed ±10% uncertainty compared to the experimental values. Similarly, V and R [38] tested the influence of combustor inlet air ratio (CIAR) on the LBO of a micro gas turbine of a swirl stabilized can-type combustor. The author used the 2D simulation method on FLUENT software by using the average exit gas temperature (AEGT) as the parameter. The result showed that the LBO limit increases with the decrease of inlet air velocity and significantly decreases with low inlet air velocity and reduction in CIAR, matching accuracy with the experimental findings with a deviation of ±6.23%. The chemical reactor network (CRN) simulation has been utilized as well for LBO prediction as seen in Kaluri et al. [39] and Gupta et al. [40]. The authors used a real-time model to predict the event of LBO by using temperature measurements in real time using the real-time chemical reactor network (RT-CRN). The input is the measured temperature and mass flow rate of fuel/air. The result showed that near LBO, a maximum concentration of hydroxy OH radicals was downstream. The difference in the concentration of OH radicals in the flame zone and recirculation zone indicates near LBO. However, the CRN approach was not easy to implement.
3. Hybrid Method
The hybrid prediction methods can be achieved by combining the semi-empirical models and numerical simulation. The semi-empirical model is used to determine several important flow field characteristics. At the same time, the numerical simulation is used for a precise flow field in the combustor. Therefore, the hybrid approaches have the potential to optimize the benefits of both of the preceding two strategies. Several hybrid approaches have been suggested and implemented, which can be divided into two: the semi-empirical based hybrid and the numerical based hybrid.
The hybrid method is a promising approach and could maximize the advantages since they combine the benefits of both models. The simplicity and robustness of the semi-empirical model and the better accuracy of the numerical model are where the inadequacies in the earlier model can be compensated. The hybrid method could have a wider range of applications while producing higher accuracy than a single method. However, more validation is needed for such a method [41]. Despite this, the hybrid model is still limited in its applicability due to its inability to be employed in a variety of combustor configurations. It is necessary to do more validation and further development on the operational circumstances, particularly the semi-empirical-based hybrid model. The relatively high level of uncertainty, which can range anywhere from 5% to 15% with such a model, is the primary downside.
4. Experimental Method
The experimental method herein refers to the use of the laboratory-scale combustor to study the LBO. As it is mimicking the lean premixed gas turbine, the flame characteristics are the most frequently used LBO prediction parameter in most setups, especially in the laboratory-scale combustors. A variety of methods were performed for LBO prediction, such as using sensors, the statistical approach, image processing using a camera or the observational method. The sensor method is mainly used for exhaust temperature detection, as documented by Rieker et al. [42], using a diode absorption sensor. However, the most recent sensor used for LBO prediction is the ion current sensor. It is simple, cheap, and easy to maintain [43]. Many experiments through the last decades with various combustors have shown that an ion current sensor with a central electrode may be installed simply in a combustor chamber without significant modification. Ion current signals may be used as a quick and reliable indication of flame conditions and essential operating parameters. The ion current sensor was used successfully to predict the LBO when mounted in a suitable position, as documented by Li et al. [44], Wollgarten et al. [45] and Chang et al. [46]. Nevertheless, ion current sensors provide weak ion current signals easily interfered with by other electronic devices and are difficult to gather by the acquisition system. Additionally, the weak signals would significantly limit the sensor’s accuracy and reliability for flame detection [43].
Many authors used the statistical approach by collecting experimental data and used an artificial intelligence (AI) technique for the LBO prediction. One of the studies documented by De et al. [47]. The authors utilized the CH* chemiluminescence data that were obtained experimentally with statistical analysis using the recurrence quantification analysis (RQA). The findings suggested that RQA could accurately predict LBO by recording the transition to LBO. However, the authors determined that adopting statistical approaches such as RQA required significant processing time. Later, the same authors [48] employed different statistical methods to determine the heat release rate variability while witnessing the flame transition toward LBO. The findings indicated that frequency analysis based on the heat release rate was appropriate for early LBO prediction and could be applied in an actual combustor. Then, recently, ref. [49] described the use of flame color to identify combustion while reaching lean blowout. The study used the RGB colors to create an anomaly measure and observed the relation with LBO. The findings indicated that the anomaly measure of the RGB successfully predicted LBO.
Furthermore, different studies analyzed the flame color by using the camera for image collections of the flame near LBO. For example, Chaudhari et al. [50] have developed a unique approach for detecting LBOs based on flame colors. They utilized a commercial CCD camera to determine the ratio of red to blue intensities in the flame picture as the LBO indicator. The experiment showed that using the ratio of red and blue is suitable for LBO detection. They were followed by the investigation of [51]. The authors confirmed the result of the previous experiment by using a similar technique of observing the red and blue color and image processing tools. Consequently, Bhattacharya et al. [52] attempted an online prediction of LBO successfully by collecting the heat release data and RGB images of the flame colors at near LBO conditions. Another experiment of flame color in addition to chemiluminescence was used to forecast LBOs, as De et al. [53] demonstrated. Two approaches were employed to capture the flame colors: a spectrometer and a charged-coupled device camera (CCD) to examine the flame’s red, green, and blue hues. The observation was made during the shift from stability to LBO-like behavior. The findings indicated that the approaches were effective at predicting LBO, particularly when combined with a spectrometer. Although the CCD camera was capable of producing a comparable forecast, it was less precise than the spectrometer.
Additionally, different methods have been used lately, as shown in Bhattacharya et al. [54]. The authors used a frequency-based fast Fourier transform (FFT) technique in time series. The experiment successfully detected the thermoacoustic instability and the change of the combustor from stability to LBO. However, the proposed method requires deep knowledge of the combustor’s acoustic mode. Furthermore, in recent years, CH* chemiluminescence image processing techniques have been widely employed to characterize the heat release and local equivalence ratio of stabilized flames [55]. OH* chemiluminescence is a common technique for capturing the flame shape [56]. Mondal et al. [57] relied on the CH* chemiluminescence. They investigated an alternative prediction approach for the lean blowout by using the AI technique of hidden Markov modeling (HMM) technique to observe the change in chemiluminescence data over time using a time series. The research mainly focused on the transition of the combustor from stable to LBO and near LBO to stable and effectively predicted LBO. Nevertheless, chemiluminescence emissions are susceptible to other species’ influence [58]. Lastly, an interesting study by Kirubakaran and Bhatt [59] by using a laboratory-scale combustor of a micro gas turbine. The authors used inlet velocity in a range of 1.70 to 11 m/s to study its effect on the LBO. The result shows that inlet velocity could be used to predict the LBO in a statistical approach and showed that inlet velocity significantly affects combustion.
5. Date-Driven Method
Historically, modern science and engineering have relied on semi-empirical-based models that are often developed to improve complicated systems’ design stages. The primary benefit of employing semi-empirical models is that they are based on simplified mathematical equations and adequately explain the topic under consideration. Unfortunately, these models need significant engineering work to construct, and in certain circumstances, reliable models are impossible to acquire owing to the system’s complicated or unknown physical and chemical reactions [60]. On the other side, the recent exponential expansion of data enables the creation and dissemination of novel techniques that are entirely data-driven [61][62][63]. These data-driven models may be constructed more simply by gathering measurements taken over the system’s operational range and then learning or embedding the connection between the sensor measurements into the model architecture using mathematical approaches.
Additionally, the data-driven approach has been widely used in various fields, especially for performance enhancement and fault prediction. In the area of gas turbines, the data-driven approach has been used exponentially for fault detection, such as detecting the fault in the gas turbine engine sensors as demonstrated by Naderi and Khorasani [64], Pourbabaee et al. [65], Navi et al. [66], and Cartocci et al. [67]. Similarly, it was used for aircraft engine health prediction, as demonstrated by Bathaie and Khorasani [68], Liu [69] and Liu et el. [70]. It was also used to predict gas turbine system degradation over time by Olsson et al. [71] and Sanaye et al. [72]. The previous studies show the data-driven technique’s robust performance and high-accuracy fault prediction. Regarding LBO prediction, the fully data-driven approach is a promising technique to achieve the highest performance and accuracy. Multiple indicators could be used to accurately predict the LBO, such as the fuel/air ratio, sudden drop in load, and flame temperature, which are essential parameters found in most historical data in the LPM gas turbines.
References
- Lei, S.; Yong, H. An overview of methodologies to predict lean blowout limits for gas turbine combustors. In Proceedings of the 2019 16th International Bhurban Conference on Applied Sciences and Technology (IBCAST), Islamabad, Pakistan, 8–12 January 2019; pp. 709–718.
- Zukoski, E.E.; Marble, F.E. Experiments concerning the mechanism of flame blowoff from bluff bodies. Caltech 1983. Available online: https://resolver.caltech.edu/CaltechAUTHORS:20110203-125953778 (accessed on 6 October 2022).
- Plee, S.; Mellor, A. Review of flashback reported in prevaporizing/premixing combustors. Combust. Flame 1978, 32, 193–203.
- Plee, S.L.; Mellor, A.M. Characteristic time correlation for lean blowoff of bluff-body-stabilized flames. Combust. Flame 1979, 35, 61–80.
- Derr, W.S.; Mellor, A.M. Characteristic times for lean blowoff in turbine combustors. J. Propuls. Power 1987, 3, 377–380.
- Jarymowycz, T.A.; Mellor, A.M. Correlation of lean blowoff in an annular combustor. J. Propuls. Power 1986, 2, 190–192.
- Leonard, P.; Mellor, A. Correlation of lean blowoff of gas turbine combustors using alternative fuels. J. Energy 1983, 7, 729–732.
- Longwell, J.P.; Frost, E.E.; Weiss, M.A. Flame Stability in Bluff Body Recirculation Zones. Ind. Eng. Chem. 1953, 45, 1629–1633.
- Lefebvre, A. Fuel effects on gas turbine combustion—ignition, stability, and combustion efficiency. J. Eng. Gas Turbines Power. 1985, 107, 24–37.
- Lefebvre, A.H.; Ballal, D.R. Gas Turbine Combustion: Alternative Fuels and Emissions; CRC Press: Boca Raton, FL, USA, 2010.
- Ballal, D.R.; Lefebvre, A.H. Weak Extinction Limits of Turbulent Flowing Mixtures. J. Eng. Power 1979, 101, 343–348.
- Ateshkadi, A.; McDonell, V.G.; Samuelsen, G.S. Lean blowout model for a spray-fired swirl-stabilized combustor. Proc. Combust. Inst. 2000, 28, 1281–1288.
- Mongia, H.; Vermeersch, M.; Held, T. A simple reactor-based approach for correlating lean blowout of turbopropulsion engine combustors. In Proceedings of the 37th Joint Propulsion Conference and Exhibit, Salt Lake City, UT, USA, 8–11 July 2001; p. 3420.
- Mongia, H.; Vermeersch, M.; Held, T. Data Reduction and Analysis (DRA) for Emissions and Lean Blowout. In Proceedings of the 41st Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 2003.
- Xie, F.; Huang, Y.; Hu, B.; Wang, F. Improved Semiempirical Correlation to Predict Lean Blowout Limits for Gas Turbine Combustors. J. Propuls. Power 2012, 28, 197–203.
- Ahmed, E.; Yong, H. Prediction of lean blowout performance of gas turbine combustor based on flow structures. Aeronaut. J. 2017, 122, 238–259.
- Sun, L.; Huang, Y.; Wang, R.; Feng, X.; Liu, Z.; Wu, J. FV-MP model to predict lean blowout limits for multi-point lean direct injection combustors. Aerosp. Sci. Technol. 2019, 88, 185–192.
- Rowen, W.I. Simplified Mathematical Representations of Heavy-Duty Gas Turbines. J. Eng. Power 1983, 105, 865–869.
- Omar, M.; Ibrahim, R.; Abdullah, M.F.; Tarik, M.H.M. Modelling and System Identification of Gas Fuel Valves in Rowen’s Model for Dry Low Emission Gas Turbine. In Proceedings of the 2018 IEEE Conference on Big Data and Analytics (ICBDA), Langkawi, Kedah, Malaysia, 21–22 November 2018; pp. 33–37.
- Omar, M.; Tarik, M.H.M.; Ibrahim, R.; Abdullah, M.F. Suitability study on using rowen’s model for dry-low emission gas turbine operational performance. In Proceedings of the TENCON 2017—2017 IEEE Region 10 Conference, Penang, Malaysia, 5–8 November 2017; pp. 1925–1930.
- Omar, M.B.; Ibrahim, R.B.; Abdullah, M.F.; Tarik, M.H.M. Modelling of Dry-Low Emission Gas Turbine Fuel System using First Principle Data-Driven Method. J. Power Technol. 2020, 100, 1–13.
- Faqih, M.; Omar, M.B.; Ibrahim, R.B. Development of Rowen’s Model for Dry-Low Emission Gas Turbine Dynamic Simulation using Scilab. In Proceedings of the 2022 IEEE 5th International Symposium in Robotics and Manufacturing Automation (ROMA), Malacca, Malaysia, 6–8 August 2022; pp. 1–5.
- Hu, B.; Huang, Y.; Wang, F. FIA method for LBO limit predictions of aero-engine combustors based on FV model. Aerosp. Sci. Technol. 2013, 28, 435–446.
- Huang, Y.; Sun, L. On the Quick Prediction of Lean Blowout Limits for Gas Turbine Combustors. Destech Trans. Environ. Energy Earth Sci. 2018.
- Sun, L.; Huang, Y.; Wang, X.; Zheng, Z.; Wang, R.; Feng, X. Hybrid method based on flame volume concept for lean blowout limits prediction of aero engine combustors. Chin. J. Aeronaut. 2021, 34, 425–437.
- Akhtar, S.; Piffaretti, S.; Shamim, T. Numerical investigation of flame structure and blowout limit for lean premixed turbulent methane-air flames under high pressure conditions. Appl. Energy 2018, 228, 21–32.
- Ladeinde, F. Advanced computational-fluid-dynamics techniques for scramjet combustion simulation. AIAA J. 2010, 48, 513–514.
- Chen, J.H. Petascale direct numerical simulation of turbulent combustion—Fundamental insights towards predictive models. Proc. Combust. Inst. 2011, 33, 99–123.
- Mercier, R.; Auzillon, P.; Moureau, V.; Darabiha, N.; Gicquel, O.; Veynante, D.; Fiorina, B. Les modeling of the impact of heat losses and differential diffusion on turbulent stratified flame propagation: Application to the tu darmstadt stratified flame. Flow Turbul. Combust. 2014, 93, 349–381.
- Gonzalez-Juez, E.; Kerstein, A.; Ranjan, R.; Menon, S. Advances and challenges in modeling high-speed turbulent combustion in propulsion systems. Prog. Energy Combust. Sci. 2017, 60, 26–67.
- Ihme, M.; Pitsch, H. Prediction of extinction and reignition in nonpremixed turbulent flames using a flamelet/progress variable model: 2. Application in LES of Sandia flames D and E. Combust. Flame 2008, 155, 90–107.
- Garmory, A.; Mastorakos, E. Capturing localised extinction in Sandia Flame F with LES–CMC. Proc. Combust. Inst. 2011, 33, 1673–1680.
- Ayache, S.; Mastorakos, E. Conditional Moment Closure/Large Eddy Simulation of the Delft-III Natural Gas Non-premixed Jet Flame. Flow Turbul. Combust. 2012, 88, 207–231.
- Hasti, V.R.; Kundu, P.; Kumar, G.; Drennan, S.A.; Som, S.; Won, S.H.; Dryer, F.L.; Gore, J.P. Lean blow-out (LBO) computations in a gas turbine combustor. In Proceedings of the 2018 Joint Propulsion Conference, Cincinnati, OH, USA, 9–11 July 2018.
- Nassini, P.C.; Pampaloni, D.; Meloni, R.; Andreini, A. Lean blow-out prediction in an industrial gas turbine combustor through a LES-based CFD analysis. Combust. Flame 2021, 229, 111391.
- Schwagerus, A.; Habisreuther, P.; Zarzalis, N. Lean-Blow-Out Simulation of Natural Gas Fueled, Premixed Turbulent Jet Flame Arrays with LES and FGM-Modeling. In Proceedings of the ASME Turbo Expo 2021: Turbomachinery Technical Conference and Exposition, Combustion, Fuels, and Emissions, Online, 7–11 June 2021; Volume 3A.
- Maran, P.; Boopathi, S.; Gowtham, P.; Chidambaram, S. Prediction of Lean Blowout Limits for Methane-Air Bluff Body Stabilized Combustion using a Temperature Gradient Method in a Model Gas-Turbine Afterburner. Int. J. Turbo Jet-Engines 2020, 37, 343–352.
- Kirubakaran, V.; Naren Shankar, R. Prediction of lean blowout performance on variation of combustor inlet area ratio for micro gas turbine combustor. Aircr. Eng. Aerosp. Technol. 2021, 93, 915–924.
- Kaluri, A.; Malte, P.; Novosselov, I. Real-time prediction of lean blowout using chemical reactor network. Fuel 2018, 234, 797–808.
- Gupta, S.; Malte, P.; Brunton, S.L.; Novosselov, I. Prevention of lean flame blowout using a predictive chemical reactor network control. Fuel 2019, 236, 583–588.
- Sturgess, G.; Shouse, D. A hybrid model for calculating lean blowouts in practical combustors. In Proceedings of the 32nd Joint Propulsion Conference and Exhibit, Buena Vista, FL, USA, 1–3 July 1996.
- Rieker, G.B.; Jeffries, J.B.; Hanson, R.K.; Mathur, T.; Gruber, M.R.; Carter, C.D. Diode laser-based detection of combustor instabilities with application to a scramjet engine. Proc. Combust. Inst. 2009, 32, 831–838.
- Xu, H.; Fan, W.; Feng, J.; Yan, P.; Qi, S.; Zhang, R. Parameter Determination and Ion Current Improvement of the Ion Current Sensor Used for Flame Monitoring. Sensors 2021, 21, 697.
- Li, F.; Xu, L.; Du, M.; Yang, L.; Cao, Z. Ion current sensing-based lean blowout detection for a pulse combustor. Combust. Flame 2017, 176, 263–271.
- Wollgarten, J.C.; Zarzalis, N.; Turrini, F.; Peschiulli, A. Experimental investigations of ion current in liquid-fuelled gas turbine combustors. Int. J. Spray Combust. Dyn. 2017, 9, 172–185.
- Chang, L.; Cao, Z.; Fu, B.; Lin, Y.; Xu, L. Lean blowout detection for bluff-body stabilized flame. Fuel 2020, 266, 117008.
- De, S.; Bhattacharya, A.; Mondal, S.; Mukhopadhyay, A.; Sen, S. Application of recurrence quantification analysis for early detection of lean blowout in a swirl-stabilized dump combustor. Chaos 2020, 30, 043115.
- De, S.; Bhattacharya, A.; Mondal, S.; Mukhopadhyay, A.; Sen, S. Identification and early prediction of lean blowout in premixed flames. Sādhanā 2020, 45, 222.
- De, S.; Bhattacharya, A.; Mukhopadhyay, A.; Sen, S. Early detection of lean blowout in a combustor using symbolic analysis of colour images. Measurement 2021, 186, 110113.
- Chaudhari, R.R.; Sahu, R.P.; Ghosh, S.; Mukhopadhyay, A.; Sen, S. Flame color as a lean blowout predictor. Int. J. Spray Combust. Dyn. 2013, 5, 49–66.
- Sen, U.; Sharma, A.; Panja, S.; Mukherjee, S.; Sen, S.; Mukhopadhyay, A. Correlation of equivalence ratio with spectrometric analysis for premixed combustion. Fluid Mech. Fluid Power Contemp. Res. 2017, 1475–1483.
- Bhattacharya, A.; Gupta, B.; Hansda, S.; Haque, Z.; Kumar, A.; Mishra, M.K.; De, S.; Mukhopadhyay, A.; Sen, S. Lean Blowout Phenomena and Prior Detection of Lean Blowout in a Premixed Model Annular Combustor. In Proceedings of the Gas Turbine India Conference. American Society of Mechanical Engineers, Online, 29 November 2021; Volume 83532, p. V002T04A009.
- De, S.; Biswas, A.; Bhattacharya, A.; Mukhopadhyay, A.; Sen, S. Use of Flame Color and Chemiluminescence for Early Detection of Lean Blowout in Gas Turbine Combustors at Different Levels of Fuel–Air Premixing. Combust. Sci. Technol. 2019, 192, 933–957.
- Bhattacharya, C.; De, S.; Mukhopadhyay, A.; Sen, S.; Ray, A. Detection and classification of lean blow-out and thermoacoustic instability in turbulent combustors. Appl. Therm. Eng. 2020, 180, 115808.
- Klusmeyer, A.; Cross, C.; Lubarsky, E.; Bibik, O.; Shcherbik, D.; Zinn, B. Prediction of blow-offs of bluff body stabilized flames utilizing close-coupled injection of liquid fuels. J. Eng. Gas Turbines Power 2013, 135, 011504.
- Chen, Y.; Fan, Y.; Han, Q.; Shan, X.; Bi, Y.; Deng, Y. The influence of cooling air jets on the premixed flame structure and stability of air-cooled bluff-body flameholder. Fuel 2022, 310, 122239.
- Mondal, S.; De, S.; Mukhopadhyay, A.; Sen, S.; Ray, A. Early Prediction of Lean Blowout from Chemiluminescence Time Series Data. Combust. Sci. Technol. 2020, 194, 1108–1135.
- Docquier, N.; Candel, S. Combustion control and sensors: A review. Prog. Energy Combust. Sci. 2002, 28, 107–150.
- Kirubakaran, V.; Bhatt, D. Experimental Prediction of Lean Blowout Limits for 3kW Micro Gas Turbine Combustor fuelled with LPG. Incas Bull. 2021, 13, 89–95.
- Iannitelli, M.; Allegorico, C.; Garau, F.; Capanni, M. A Hybrid Model for on-line Detection of Gas Turbine Lean Blowout Events. PHM Soc. Eur. Conf. 2018, 4.
- Yan, W.; Yu, L. On accurate and reliable anomaly detection for gas turbine combustors: A deep learning approach. arXiv 2019, arXiv:1908.09238.
- Roman, R.C.; Precup, R.E.; Petriu, E.M.; Dragan, F. Combination of data-driven active disturbance rejection and Takagi-Sugeno fuzzy control with experimental validation on tower crane systems. Energies 2019, 12, 1548.
- Hashemi, S.M.; Botez, R.M.; Grigorie, T.L. New reliability studies of data-driven aircraft trajectory prediction. Aerospace 2020, 7, 145.
- Naderi, E.; Khorasani, K. Data-driven fault detection, isolation and estimation of aircraft gas turbine engine actuator and sensors. Mech. Syst. Signal Process. 2018, 100, 415–438.
- Pourbabaee, B.; Meskin, N.; Khorasani, K. Robust sensor fault detection and isolation of gas turbine engines subjected to time-varying parameter uncertainties. Mech. Syst. Signal Process. 2016, 76, 136–156.
- Navi, M.; Davoodi, M.R.; Meskin, N. Sensor fault detection and isolation of an industrial gas turbine using partial kernel PCA. IFAC-PapersOnLine 2015, 48, 1389–1396.
- Cartocci, N.; Napolitano, M.R.; Costante, G.; Valigi, P.; Fravolini, M.L. Aircraft robust data-driven multiple sensor fault diagnosis based on optimality criteria. Mech. Syst. Signal Process. 2022, 170, 108668.
- Tayarani-Bathaie, S.S.; Khorasani, K. Fault detection and isolation of gas turbine engines using a bank of neural networks. J. Process. Control 2015, 36, 22–41.
- Liu, J. Gas path fault diagnosis of aircraft engine using HELM and transfer learning. Eng. Appl. Artif. Intell. 2022, 114, 105149.
- Liu, S.; Wang, H.; Tang, J.; Zhang, X. Research on fault diagnosis of gas turbine rotor based on adversarial discriminative domain adaption transfer learning. Measurement 2022, 196, 111174.
- Olsson, T.; Ramentol, E.; Rahman, M.; Oostveen, M.; Kyprianidis, K. A data-driven approach for predicting long-term degradation of a fleet of micro gas turbines. Energy AI 2021, 4, 100064.
- Sanaye, S.; Hosseini, S. Prediction of blade life cycle for an industrial gas turbine at off-design conditions by applying thermodynamics, turbo-machinery and artificial neural network models. Energy Rep. 2020, 6, 1268–1285.
More
Information
Subjects:
Energy & Fuels
Contributors
MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register
:
View Times:
1.7K
Revisions:
2 times
(View History)
Update Date:
30 Nov 2022
Notice
You are not a member of the advisory board for this topic. If you want to update advisory board member profile, please contact office@encyclopedia.pub.
OK
Confirm
Only members of the Encyclopedia advisory board for this topic are allowed to note entries. Would you like to become an advisory board member of the Encyclopedia?
Yes
No
${ textCharacter }/${ maxCharacter }
Submit
Cancel
Back
Comments
${ item }
|
More
No more~
There is no comment~
${ textCharacter }/${ maxCharacter }
Submit
Cancel
${ selectedItem.replyTextCharacter }/${ selectedItem.replyMaxCharacter }
Submit
Cancel
Confirm
Are you sure to Delete?
Yes
No




