1. History

1.1. Philosophical Atomism

The idea that matter is made up of discrete units is a very old. Democritus (c.460–c.370 BC) called these units atoms. He taught that atoms were infinite in number, uncreated, and eternal, and that the qualities of an object result from the kind of atoms that compose it. ^[1][2][3]

1.2. Quantum Physical Models of Atoms

In 1924, Louis de Broglie proposed that all moving particles—particularly subatomic particles such as electrons—exhibit a degree of wave-like behavior. Erwin Schrödinger, fascinated by this idea, explored whether or not the movement of an electron in an atom could be better explained as a wave rather than as a particle. Schrödinger's equation, published in 1926,^[4] describes an electron as a wave function instead of as a point particle. This approach elegantly predicted many of the spectral phenomena that Bohr's model failed to explain. One of its critics, Max Born, proposed instead that Schrödinger's wave function did not describe the physical extent of an electron (like a charge distribution in classical electromagnetism), but rather gave the probability that an electron would, when measured, be found at a particular point.^[5] This reconciled the ideas of wave-like and particle-like electrons: the behavior of an electron, or of any other subatomic entity, has both wave-like and particle-like aspects.^[6] The precise mathematical statement of the position-momentum uncertainty principle is due to Earle Hesse Kennard, Wolfgang Pauli, and Hermann Weyl.^[7][8]) This invalidated Bohr's model, with its neat, clearly defined circular orbits. The modern model of the atom describes the positions of electrons in an atom in terms of probabilities. An electron can potentially be found at any distance from the nucleus, but, depending on its energy level and angular momentum, exists more frequently in certain regions around the nucleus than others; this pattern is referred to as its atomic orbital. ^[9] The shapes of atomic orbitals are found by solving the Schrödinger equation; however, analytic solutions of the Schrödinger equation are known for very few relatively simple model Hamiltonians including the hydrogen atom. Even the helium atom—which contains just two electrons—has defied all attempts at a fully analytic treatment.

1.3. Attempts to Visualize the Shapes of Atoms

Schrödinger's equation makes it possible to find exactly the electron cloud density for a hydrogen atom with one electron^[10] (left), and with some approximation for a covalent bond forming H₂ (right) where two hydrogen atoms share the two electrons ^[11]. https://handwiki.org/wiki/index.php?curid=2010422

The plum pudding model is first model of an atom shape. This model is proposed by J. J. Thomson in 1904.^[12], soon after the discovery of the electron. In 1911, Ernest Rutherford, an experiment with scattering alpha particles showed that a positively charged substance is concentrated in the nucleus, which is at least 3,000 times smaller than the size of an atom. Erwin Schrödinger, Werner Heisenberg and others led to the full development of quantum mechanics in the mid-1920s, which showed the rotational motion of light electrons around a heavy nucleus. Electrons fill the entire volume of the atom. In this regard, Richard Feynman^[13]proposed to consider an atom in the form of a cloud, whose electron cloud density is proportional to the probability density for observing the electron. Thus “picture” of an atom is a nucleus surrounded by an “electron cloud”.

2. Electron Cloud Density of Atoms, Molecules and Chemical Bonds

Photos of the electron cloud density ρ(x,y): a) carbon nanotube; ^[14] b) rudenite;^[15] c) covalent chemical bonds in crystalline silicon; ^[16] d)a separate molecule of pentane^[17]. https://handwiki.org/wiki/index.php?curid=1477433

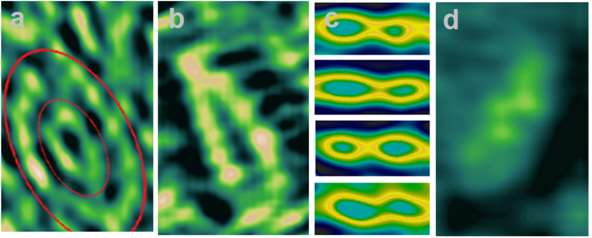
In its efforts to learn as much as possible about nature, modern physics has found that electron clouds can be “known” with certainty. Direct visualization of individual electron cloud was obtained in 2018 Olexandr P. Kucherov a physicist from Ukraine .^[17] Direct visualization of small objects studied by chemistry is made possible by the discovery of the electron beam shifting in accordance with the electron cloud density. Accordance with this effect, an atom begins to illuminate, depicting its own form! A quantum mechanical theory of the effect is given. As a result, it was possible to trace a chemical reaction with a change in the chemical bonds, geometry molecules, and distances between atoms.

3. Electron Cloud Density of an Individual Carbon Atom

Electron clouds density ρ(x,y) of carbon atom (left) in crystalline graphite (right) visualized with 10 pm resolution by means of the electron beam shifting effect;^[18] . https://handwiki.org/wiki/index.php?curid=1237590

Electron cloud densitometry was used to visualize crystalline graphite along with internal orbitals and valence electrons. Photo on the left shows how six electrons form a complex shape of a carbon atom ₆C. Tow core electrons create pink sphere in the center. One valence electron forms weak π bond (blue) and three valence electrons form strong σ bonds sp² orbital hybrids left, right (green) and behind from the center of the carbon atom. The color scale of the electron cloud density ρ(x,y) is given as a percentage. A space around the atom is mostly black because there is zero density of the electron cloud.

Photo on the right shows crystalline carbon where the atoms (pink spheres) are arranged in layers that are connected by strong σ bonds sp² orbital hybrids (green), while the weak π bonds (blue) extend between the layers.

4. Quantum Mechanics Theory of the Electron Beam Shifting Effect

In the mathematically rigorous formulation of quantum mechanics, the state of a quantum mechanical system is a wave function Ψ. The wave function Ψ₁₂(q₁,q₂) with coordinates q₁,q₂, describes the state of a composite systems consisting of en electron cloud of the testing sample Ψ₁(q₁) and plane wave of the electron beam which propagates along the axis z:

Ψ2(z) = √j exp (ikz) , 

where j – electron beam density; k - constant for a plane wave. Respectively, the screen of the electron densitometer is in the plane x,y.

According to quantum superposition, the wave function of the composite systems is the product of these two wave functions:

Ψ12(q1,q2) = Ψ1(q1) √j exp (ikz). 

The probability ρ (x, y) to find an electron at the point x,y of the densitometer screen is the integral over all the coordinates of the plane wave and the coordinate z of the wave function of the electrons of the atom:

ρ (x, y) = ʃ Ψ12(q1,q2) Ψ*12(q1,q2) dq1dz. 

The integral over the coordinates dq₁ of a plane wave is equal to j, the square of the modulus. Under the integral remains the density of the electron cloud:

ρ(x, y) = jnʃρ(x,y,z) dz, 

where ρ (x, y, z) is the probability of finding an electron in the volume dx, dy, dz of an atom which satisfies the normalization condition:

1 = ʃʃʃρ(x,y,z) dx, dy, dz. 

Note that the normalization condition must be satisfied for each of the n electrons in the atom. Finally, the relationship between the intensity of the electron beam and the density of the electron cloud at the point x, y takes the form:

I (x, y) = jnρ(x,y), 

where n is the number of electrons in the atom.^[18]

As a result, the intensity of the electron beam passing through the electron cloud of the testing sample at the point x, y is directly proportional to the density of the electron cloud in the column at that point. It is the essence of the electron beam shifting effect.

The expression was obtained in general on the basis of quantum mechanics. The integral of the wave functions found from the Schrödinger equation and the superposition principle was taken.

5. Application

The photo shows a Rudenite,^[18] the superdense film of two layers of flat hexagonal grapheme: a) Spatial ball-match 3D model of rudenite; b) side view; c) for comparison on the same scale with the model is a photo of electronic clouds of rudenite, side view. https://handwiki.org/wiki/index.php?curid=1128535

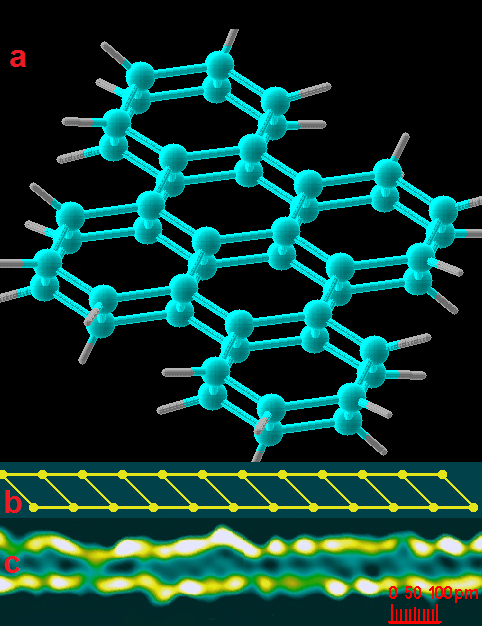
Electron cloud densitometry makes it possible to study in some detail the mutual arrangement of atoms in a molecule and the shape of chemical bonds, as well as to follow the ways in which chemical reactions take place. As a result of the use of electron cloud densitometry, Rudenite was found, which is a superdense allotropic form carbon with a two-layer diamond-like structure^[15] whose existence was later confirmed by an independent group of scientists.^[19] Subsequently, by electron cloud densitometry, this substance was synthesized in an amount sufficient for laboratory studies^[18]