
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Siyuan Zhang | -- | 2052 | 2022-11-18 02:21:58 | | | |
| 2 | Amina Yu | + 2 word(s) | 2054 | 2022-11-18 03:54:55 | | |
Video Upload Options
Contact and friction are closely related to the engineering industry, especially in the technologies associated with rolling bearing, wheel–rail control, head–disk interaction and so on. Therefore, which factors are related to the contact mechanical properties of solid surface and how to design and control the interface friction coefficient are hot issues in scientific research and engineering practice. In fact, the contact behavior and friction properties are closely related to the microstructure of the contact surface. Based on the accurate characterizations of the surface topography, the corresponding research can start from the local contact model, investigating the contact and friction relationships of each contact asperity of the rough surface, and finally accurately predicting the contact relationships and friction performances of the interfaces.
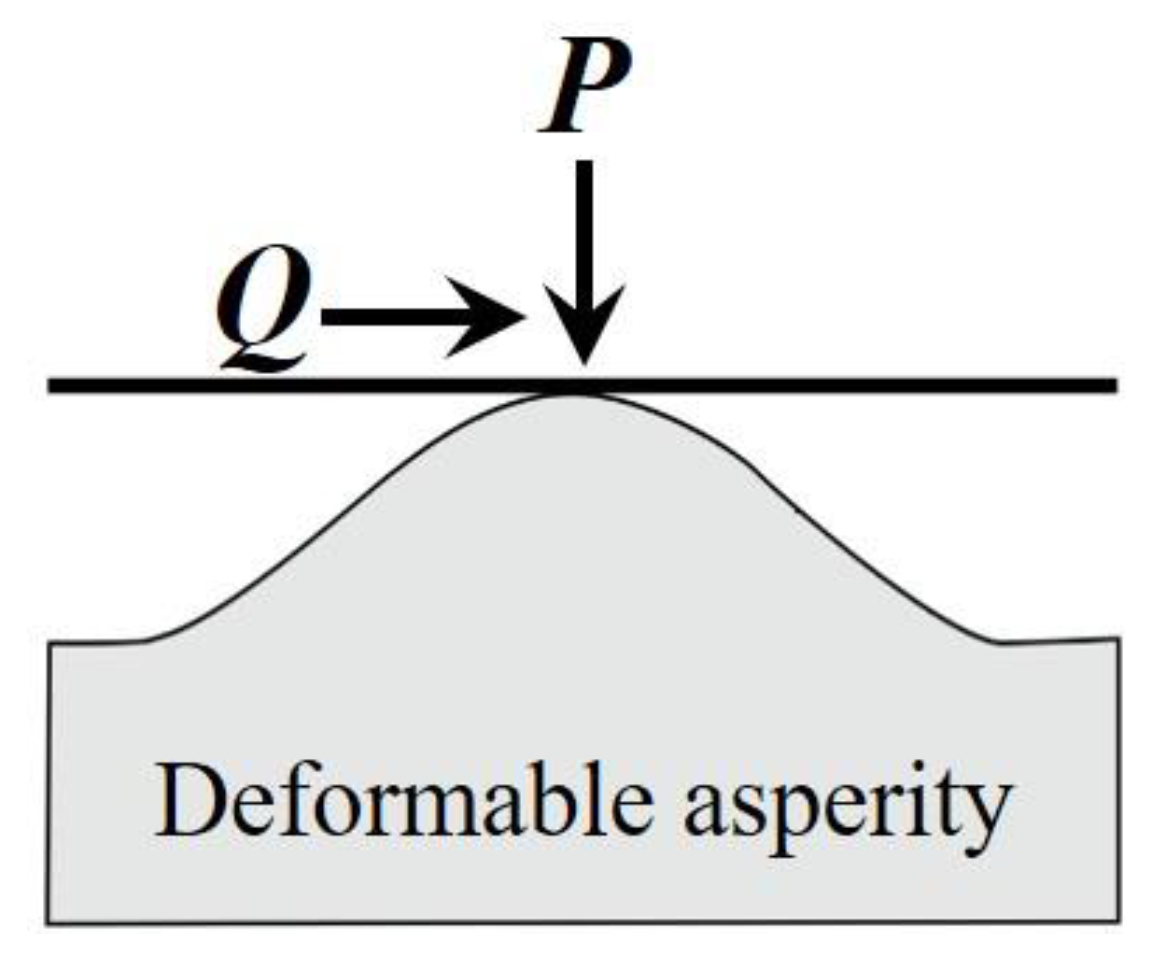
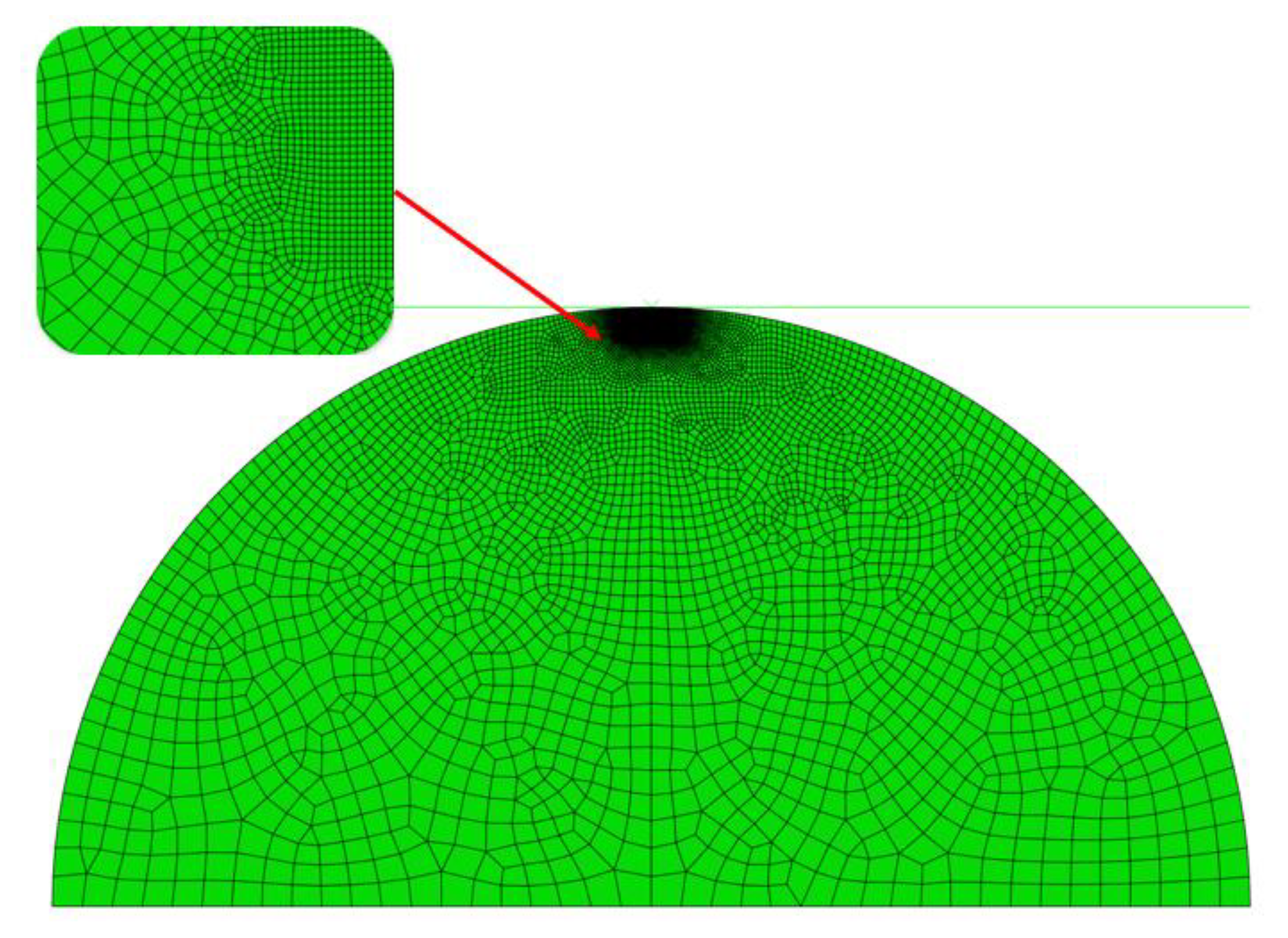
1. Friction and Slip Behaviors of a Single Asperity
2. Examples of Interface Friction Behavior Standing on Contact Mechanics
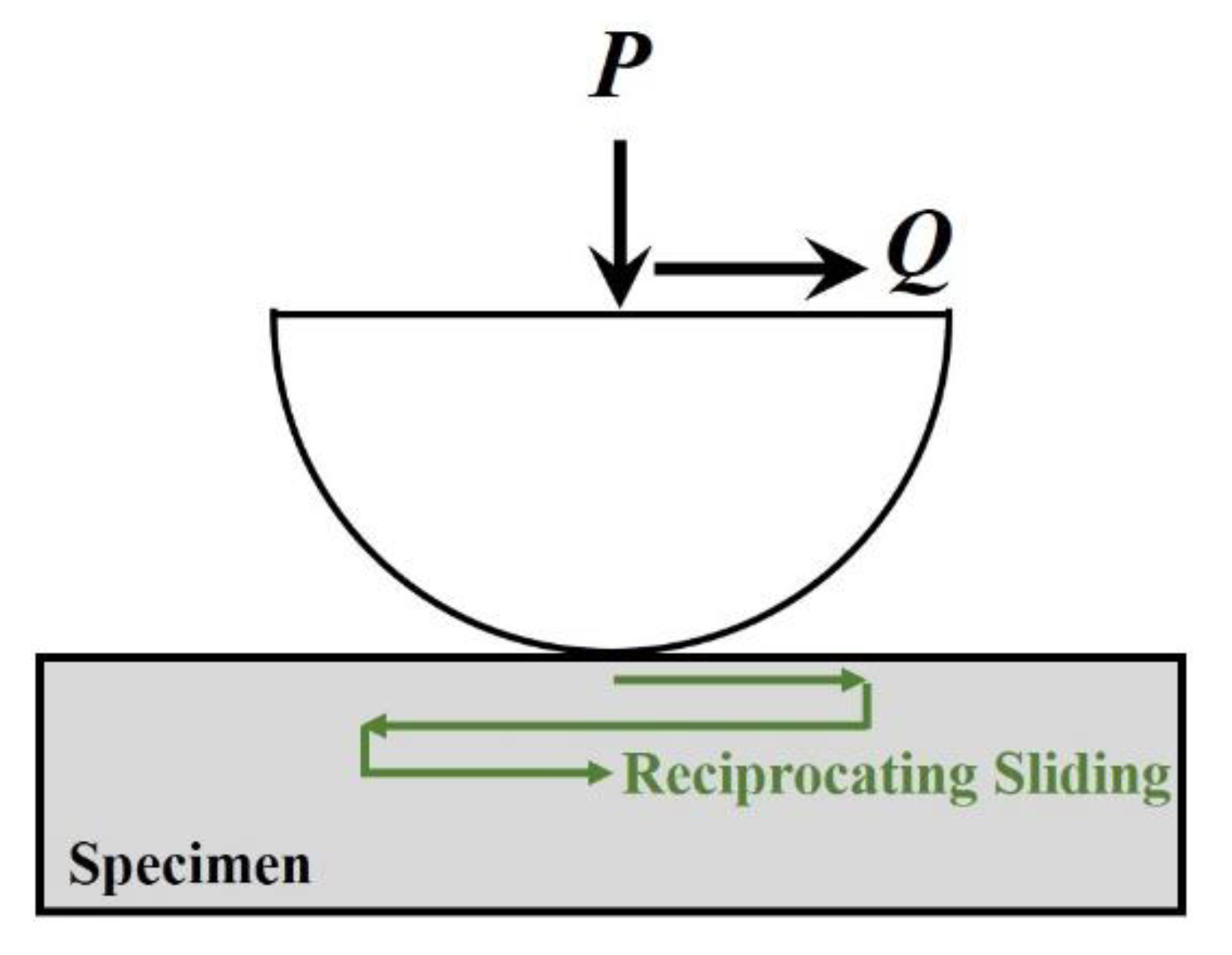
3. Experimental Methods for Friction Studies
References
- Mindlin, R.D. Compliance of Elastic Bodies in Contact. J. Appl. Mech. 1949, 16, 259–268.
- Hamilton, G.M. Explicit Equations for the Stresses beneath a Sliding Spherical Contact. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 1983, 197, 53–59.
- Chang, W.-R.; Etsion, I.; Bogy, D.B. Static Friction Coefficient Model for Metallic Rough Surfaces. J. Tribol. 1988, 110, 57–63.
- Kogut, L.; Etsion, I. A Semi-Analytical Solution for the Sliding Inception of a Spherical Contact. J. Tribol. 2003, 125, 499–506.
- Brizmer, V.; Kligerman, Y.; Etsion, I. The effect of contact conditions and material properties on the elasticity terminus of a spherical contact. Int. J. Solids Struct. 2006, 43, 5736–5749.
- Zait, Y.; Kligerman, Y.; Etsion, I. Unloading of an elastic–plastic spherical contact under stick contact condition. Int. J. Solids Struct. 2010, 47, 990–997.
- Etsion, I.; Kligerman, Y.; Kadin, Y. Unloading of an elastic–plastic loaded spherical contact. Int. J. Solids Struct. 2005, 42, 3716–3729.
- Ronen, S.; Goltsberg, R.; Etsion, I. A comparison of stick and slip contact conditions for a coated sphere compressed by a rigid flat. Friction 2017, 5, 326–338.
- Brizmer, V.; Kligerman, Y.; Etsion, I. Elastic–plastic spherical contact under combined normal and tangential loading in full stick. Tribol. Lett. 2006, 25, 61–70.
- Wu, A.; Shi, X. Numerical Investigation of Adhesive Wear and Static Friction Based on the Ductile Fracture of Junction. J. Appl. Mech. 2013, 80, 041032.
- Shi, X.; Wu, A.; Zhu, C.; Qu, S. Effects of load configuration on partial slip contact between an elastic-plastic sphere and a rigid flat. Tribol. Int. 2013, 61, 120–128.
- Wu, A.; Shi, X.; Polycarpou, A.A. An Elastic-Plastic Spherical Contact Model Under Combined Normal and Tangential Loading. J. Appl. Mech. 2012, 79, 051001.
- Shi, X. On Slip Inception and Static Friction for Smooth Dry Contact. J. Appl. Mech. 2014, 81, 121005.
- Xie, W.; Liu, C.; Huang, G.; Jiang, D.; Jin, J. Nano-sized single-asperity friction behavior: Insight from molecular dynamics simulations. Eur. J. Mech.-A/Solids 2022, 96, 104760.
- Xu, Y.; Scheibert, J.; Gadegaard, N.; Mulvihill, D.M. An asperity-based statistical model for the adhesive friction of elastic nominally flat rough contact interfaces. J. Mech. Phys. Solids 2022, 164, 104878.
- Maier, M.; Pusterhofer, M.; Summer, F.; Grün, F. Validation of statistic and deterministic asperity contact models using experimental Stribeck data. Tribol. Int. 2021, 165, 107329.
- Jamshidi, H.; Tavakoli, E.; Ahmadian, H. Modeling polymer-metal frictional interface using multi-asperity contact theory. Mech. Syst. Signal Process. 2021, 164, 108227.
- Wu, C.; Zhang, L.; Qu, P.; Li, S.; Jiang, Z.; Wu, Z. A multiscale soft-contact modelling method for rough surfaces in contact with coupled slipping/sliding and rolling. Tribol. Int. 2022, 173, 107627.
- Salari, S.; Beheshti, A. Asperity-based contact and static friction with provision for creep: A review. Surfaces Interfaces 2021, 24, 101144.
- Kang, H.; Li, Z.-M.; Liu, T.; Zhao, G.; Jing, J.; Yuan, W. A novel multiscale model for contact behavior analysis of rough surfaces with the statistical approach. Int. J. Mech. Sci. 2021, 212, 106808.
- Mergel, J.C.; Scheibert, J.; Sauer, R.A. Contact with coupled adhesion and friction: Computational framework, applications, and new insights. J. Mech. Phys. Solids 2020, 146, 104194.
- Hu, H.; Batou, A.; Ouyang, H. An Isogeometric analysis based method for frictional elastic contact problems with randomly rough surfaces. Comput. Methods Appl. Mech. Eng. 2022, 394, 114865.
- Fouvry, S.; Wendler, B.; Liskiewicz, T.; Dudek, M.; Kolodziejczyk, L. Fretting wear analysis of TiC/VC multilayered hard coatings: Experiments and modelling approaches. Wear 2004, 257, 641–653.
- Kartal, M.; Mulvihill, D.; Nowell, D.; Hills, D. Measurements of pressure and area dependent tangential contact stiffness between rough surfaces using digital image correlation. Tribol. Int. 2011, 44, 1188–1198.
- Kartal, M.E.; Mulvihill, D.M.; Nowell, D.; Hills, D.A. Determination of the Frictional Properties of Titanium and Nickel Alloys Using the Digital Image Correlation Method. Exp. Mech. 2010, 51, 359–371.
- Mulvihill, D.; Kartal, M.; Olver, A.; Nowell, D.; Hills, D. Investigation of non-Coulomb friction behaviour in reciprocating sliding. Wear 2011, 271, 802–816.
- Cao, H.; Zhou, X.; Li, X.; Lu, K. Friction mechanism in the running-in stage of copper: From plastic deformation to delamination and oxidation. Tribol. Int. 2017, 115, 3–7.
- Nunez, E.E.; Polycarpou, A.A. The effect of surface roughness on the transfer of polymer films under unlubricated testing conditions. Wear 2015, 326–327, 74–83.
- Fridrici, V.; Fouvry, S.; Kapsa, P. Fretting Wear behavior of a Cu–Ni–In plasma coating. Surf. Coat. Technol. 2003, 163–164, 429–434.
- Fujimoto, T.; Kagami, J.; Kawaguchi, T.; Hatazawa, T. Micro-displacement characteristics under tangential force. Wear 2000, 241, 136–142.
- Filippi, S.; Akay, A.; Gola, M.M. Measurement of Tangential Contact Hysteresis During Microslip. J. Tribol. 2004, 126, 482–489.
- Królikowski, J.; Szczepek, J. Prediction of contact parameters using ultrasonic method. Wear 1991, 148, 181–195.
- Dwyer-Joyce, R.; Drinkwater, B.W.; Quinn, A.M. The Use of Ultrasound in the Investigation of Rough Surface Interfaces. J. Tribol. 2000, 123, 8–16.
- Baltazar, A.; Rokhlin, S.I.; Pecorari, C. On the relationship between ultrasonic and micromechanical properties of contacting rough surfaces. J. Mech. Phys. Solids 2002, 50, 1397–1416.
- Gonzalez-Valadez, M.; Baltazar, A.; Dwyer-Joyce, R. Study of interfacial stiffness ratio of a rough surface in contact using a spring model. Wear 2010, 268, 373–379.
- Hills, D.A.; Nowell, D. Mechanics of fretting fatigue-Oxford’s contribution. Tribol. Int. 2014, 76, 1–5.
- Mulvihill, D.M.; Brunskill, H.; Kartal, M.E.; Dwyer-Joyce, R.S.; Nowell, D. A Comparison of Contact Stiffness Measurements Obtained by the Digital Image Correlation and Ultrasound Techniques. Exp. Mech. 2013, 53, 1245–1263.
- Mulvihill, D.; Kartal, M.; Nowell, D.; Hills, D. An elastic–plastic asperity interaction model for sliding friction. Tribol. Int. 2011, 44, 1679–1694.
- Eriten, M.; Polycarpou, A.A.; Bergman, L.A. Surface Roughness Effects on Energy Dissipation in Fretting Contact of Nominally Flat Surfaces. J. Appl. Mech. 2010, 78, 021011.
- Jin, O.; Mall, S. Effects of slip on fretting behavior: Experiments and analyses. Wear 2004, 256, 671–684.
- Yue, T.; Wahab, M.A. Finite element analysis of fretting wear under variable coefficient of friction and different contact regimes. Tribol. Int. 2017, 107, 274–282.
- Muser, M.H. How static is static Friction? Proc. Natl. Acad. Sci. USA 2008, 105, 13187–13188.
- Ben-David, O.; Cohen, G.; Fineberg, J. The Dynamics of the Onset of Frictional Slip. Science 2010, 330, 211–214.
- Carpick, R.W. Controlling Friction. Science 2006, 313, 184–185.
- Service, R.F. The Power of Friction. Science 2013, 339, 20–21.
- Etsion, I. Comment on Leonardo da Vinci’s Friction Experiments: An Old Story Acknowledged and Repeated. Tribol. Lett. 2015, 58, 33.
- Popov, V.L. Is Tribology Approaching Its Golden Age? Grand Challenges in Engineering Education and Tribological Research. Front. Mech. Eng. 2018, 4, 16.
- Kogut, L.; Etsion, I. A Static Friction Model for Elastic-Plastic Contacting Rough Surfaces. J. Tribol. 2004, 126, 34–40.
- Cohen, D.; Kligerman, Y.; Etsion, I. A Model for Contact and Static Friction of Nominally Flat Rough Surfaces Under Full Stick Contact Condition. J. Tribol. 2008, 130, 031401.
- Li, L.; Etsion, I.; Talke, F.E. Contact Area and Static Friction of Rough Surfaces With High Plasticity Index. J. Tribol. 2010, 132, 031401.
- Misra, A.; Huang, S. Effect of loading induced anisotropy on the shear behavior of rough interfaces. Tribol. Int. 2011, 44, 627–634.
- Jin, F.; Wan, Q.; Guo, X. Plane Contact and Partial Slip Behaviors of Elastic Layers With Randomly Rough Surfaces. J. Appl. Mech. 2015, 82, 091006.
- Chandrasekar, S.; Eriten, M.; Polycarpou, A.A. An Improved Model of Asperity Interaction in Normal Contact of Rough Surfaces. J. Appl. Mech. 2012, 80, 011025.
- Vakis, A.; Yastrebov, V.; Scheibert, J.; Nicola, L.; Dini, D.; Minfray, C.; Almqvist, A.; Paggi, M.; Lee, S.; Limbert, G.; et al. Modeling and simulation in tribology across scales: An overview. Tribol. Int. 2018, 125, 169–199.




