1. Friction and Slip Behaviors of a Single Asperity
Interfacial slip is the result of a combination of factors, including material properties, interface roughness, local slip, chemical reactions, etc. The force required for sliding has been a hot topic in the past decades. The classical study of asperity sliding originated from the Mindlin model in the 1940s [
104]. According to the Mindlin model, the contact region between two spheres consists of a central adhesion zone surrounded by an annular slip band. As the tangential load increases, the central adhesion region gradually decreases and eventually disappears because the material within the central adhesion region cannot withstand infinite traction. In contrast to Mindlin's analytical solution, Hamilton derived an explicit expression for the stress field under non-axisymmetric sliding contact [
105].
Chang et al.’s [
23] CEB friction model is one of the most famous friction models for asperity contact, as shown in
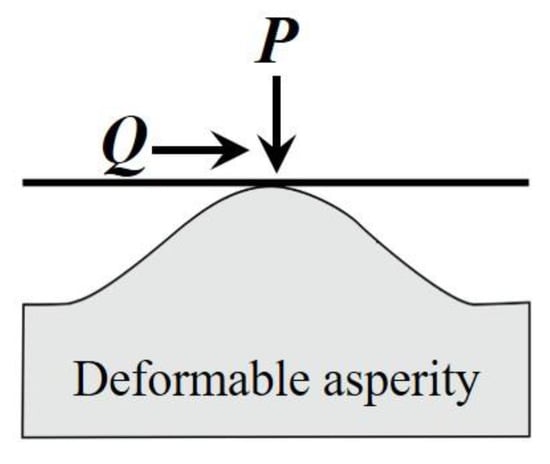
Figure 9. They assumed that sliding happens at the moment of yielding and they used the von Mises yield criterion and Hamilton's stress field to determine the maximum tangential load for a single contact asperity. Since the first yield point of a spherical contact is surrounded by a large elastic region, their results underestimate the maximum tangential load that a single contact asperity can carry.
Figure 9. A deformable asperity in contact with a rigid flat surface under combined normal and tangential loading.
When taking plasticity into consideration, Kogut et al. [
106] combined finite element analysis with analytical expressions to provide a semi-analytical solution for the sliding inception of an elastoplastic spherical contact. In another study [
107], Brizmer et al. considered local slip effects and extended the study to elastoplastic spherical contacts. They concluded that local slip conditions have a greater effect on the evolution of the plastic zone as the normal load increases. Other models have tried to discuss whether the fully adherent case [
108] or the fully slippery case [
109,
110] could be applied to real interfaces. In other studies, slip initiation conditions between deformable spheres (cylinders) and rigid flat plates were studied using finite element methods. Brizmer studied sliding friction under high adhesion conditions [
111] and extensively investigated the effect of plasticity on friction parameters such as junctional tangential stiffness, static friction force, and static friction coefficient; full adhesion conditions were used, assuming high adhesion strength. In a similar study [
112], Wu et al. investigated the adhesive friction of an elastoplastic cylinder in contact with a rigid flat plate, establishing a link between static friction and ductility. Later, in order to better characterize the friction process, Shi and Wu et al. [
113,
114,
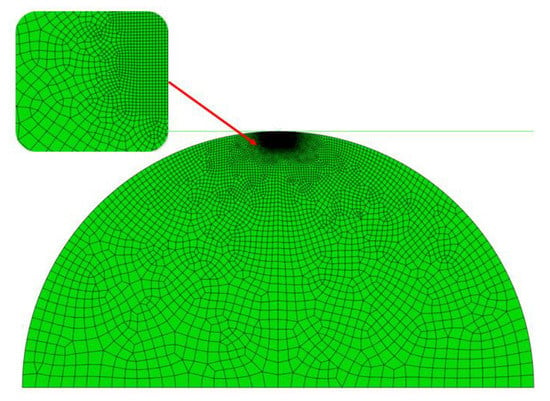
115] relaxed the all-sticky model to a partial slip state (the finite element model is shown in
Figure 10), and their proposed model revealed the friction transition between the KE model [
106] and the all-sticky model proposed by Brizmer et al. [
111] (BKE model for short). Xie et al. [
116] carried out single-asperity friction simulations by using a molecular dynamic simulation method. They analyzed stress distribution and the dislocation evolution process of single asperities. However, from the above literature review, the competing mechanisms between material plasticity and the effect of partial slip on slip initiation have not been analyzed in depth. Further studies should be carried out to investigate the friction mechanisms.
Figure 10. Schematic of finite element modeling of a spherical asperity.
2. Examples of Interface Friction Behavior Standing on Contact Mechanics
Based on the friction behavior of a single asperity and the contact mechanics of rough surfaces, Xu et al. [
117] proposed a statistical model of the contact area and friction of a soft rough interface in shear, describing the interplay between adhesion and friction at the microcontact scale. The macroscopic friction response is explained by microscopic experimental phenomena combined with microscopic scale parameters and surface statistical data. Maier et al. [
118] determined the contact pressure of real rough surfaces. They coupled the micro-model and the macro-model to consider the influence of different geometry scales on tribology behaviors. Jamshidi et al. [
119] developed a hybrid contact model of a hard rough surface on an elastic substrate by using the multi-asperity contact theory. They obtained interface physical characteristics such as initial tangential interface stiffness, slippage friction force, and maximum pre-slip displacement based on the asperity contact theory. Wu et al. [
120] presented a statistical analysis for the microscale flattening of random surface asperities. They developed a multiscale soft-contact modelling method for rough surfaces contact, in order to characterize the rough surfaces in contact with coupled slipping/sliding and rolling. Salari et al. [
121] introduced the research progress of frictional creep model based on the rough elastoplastic contact model. Kang et al. [
122] established a new contact model for rough interfaces, which was characterized by multiscale topography parameters. They revealed the effects of the multiscale topographies on the normal and tangential contact responses. Mergel et al. [
123] captured shear-induced contact area reduction in Hertzian rubber contact, and they incorporated adhesion, friction, and large deformations. They developed a computational framework, which is suitable to investigate sliding friction even under normal tensile loads. Hu et al. [
124] discussed the friction behavior between an elastic body and a rigid body with a random rough surface based on contact mechanics. According to the characteristics of random rough surface, they carried out numerical experiments on several settings, such as ‘rough–smooth’, ‘smooth–rough’, and ‘rough–rough’ contact, and discussed the affecting factors of the global coefficient of friction. These are typical examples of friction models of rough surfaces based on contact mechanics, which provides many theories and methods for further study of surface friction behavior.
3. Experimental Methods for Friction Studies
In addition to theoretical studies and numerical simulations, the evolution of interfacial friction can also be revealed from an experimental point of view. In order to fully understand the tribological phenomenon and deeply explore the mechanism of friction, wear, and lubrication, it is necessary to carry out relevant tests and analyses. The development of modern surface testing technology and instruments provides an effective means to observe surface phenomena and their changes at the atomic and molecular scales, which makes it possible to carry out experimental studies on tribology at different scales. Examples of the main instruments used for tribology experimental research are as follows: friction and wear testing machine, fretting friction and wear testing system, scanning probe microscope, friction force microscope, etc.
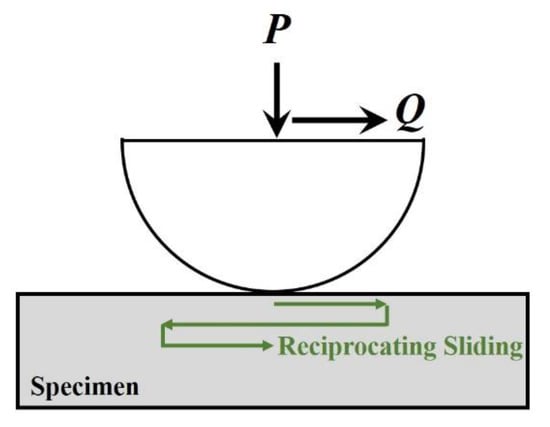
Typical experimental studies on friction coefficients are fretting friction experiments. Fretting is caused by the periodic relative displacement between two objects that are in contact. When the reciprocal motion has a sufficient number of cycles, wear occurs on or near the contact surface. Before wear occurs on the material surface, the fretting process depends on a number of factors dominated by the normal load, the tangential displacement amplitude, and the friction coefficient. Although it is possible to model the contact interface under such loading conditions, it is difficult to specify the value of the friction coefficient in the model (which may vary in space and time) without the help of experimental studies. Therefore, it is important to carry out fretting experiments. The fretting experimental setup which is commonly used is shown in Figure 11.
Figure 11. Schematic diagram of fretting experiment.
In terms of material selection for fretting experiments, the most commonly used materials are titanium alloys [
125,
126], followed by nickel alloys [
127,
128], pure copper [
129], polymers [
130], etc. Commonly used titanium alloys (Ti-6Al-4V) have low density and good mechanical properties and are commonly used in the dovetail contact area of gas turbine blade/disc attachments. However, titanium alloys have poor tribological properties and tend to have premature crack sprouting due to fretting.
As for fretting experimental methods and measurement equipment, traditional measurement methods, such as extensometers [
131] and differential transformers [
132], can be used to investigate fretting tribological properties by measuring tangential contact stiffness, but these measurements usually underestimate the stiffness values because of the inclusion of volumetric flexibility contributions. In addition to traditional methods, techniques such as laser interferometry [
133] and ultrasound have also been used to investigate the tangential stiffness of contact surfaces [
134,
135,
136,
137].
Oxford University has a long history of studying fretting fatigue [
138]. Kartal et al. [
127] developed a digital image correlation (DIC) technique to characterize the frictional properties of rough contact surfaces, using optical methods to overcome this limitation of not being able to measure full-field displacements.
Mulvihill et al. [
139] compared the frictional properties obtained by DIC and ultrasonic contact stiffness measurements obtained by ultrasonic techniques. Through finite element simulations and experiments, Mulvihill et al. [
140] concluded that friction is caused by plasticity and tangential interface adhesion. Eriten et al. [
141] investigated the effect of surface roughness on energy dissipation in friction problems between rough surfaces, and verified the analytical result that rough surfaces dissipate more energy than smooth surfaces. Mulvihill et al. [
128] investigated the increase in frictional forces during the fretting process as a result of wear-scar interactions.
Cao et al. [
129] investigated the surface morphology and the microstructure evolution of pure copper materials. They investigated the friction mechanism in the wear phase and its influence on the subsequent steady state. Jin et al. [
142] compared experimental and finite element simulation results to investigate the effect of partial slip on the performance of fretting and established a fretting diagram by using fretting fatigue life, relative slip range, and normal force. Through simulations and experiments, Yue et al. [
143] concluded that the use of variable friction coefficient has little effect on the amount of wear at the end of the steady-state phase of the fretting.
Since the contact interface in engineering is not completely smooth, sliding and friction between two rough surfaces are important [
144,
145]. In sliding contact problems, where sometimes friction needs to be reduced [
146], and sometimes friction needs to be exploited [
147], the traditional Cullen's law of friction is not applicable in all cases [
148]. Despite the long history of tribological research and the great progress made in recent years in the contact mechanics of rough surfaces, there are still many open topics in the field of friction on rough surfaces [
149]. The friction analysis based on statistical models is still the most commonly used in current friction studies on rough surfaces [
150,
151,
152,
153,
154].
In fact, the physical processes that determine friction characteristics are complex: there are contact interactions [
70], adsorption, adhesion [
155], material properties, etc. It is difficult to predict the friction coefficients of actual friction pairs by means of simplified numerical models and to really understand what the main control parameters are. Therefore, it is necessary to take the simplified friction model commonly used in two rough surface sliding problems as an example to reveal the influencing factors of interfacial sliding and friction coefficients from theoretical, simulation, and experimental perspectives by releasing the assumptions of traditional friction models for material and interfacial sliding criteria.
Most current theoretical and simulation studies on interfacial sliding and friction mechanisms investigate the plastic effect in a fully adhesion model or local slip in a Mindlin framework. There are few studies on the mechanism of the transition from plastic yielding to full slip at the early stage of sliding, and an accurate prediction of it is still lacking. Therefore, models are needed to analyze the competing mechanisms between these two factors and provide a quantitative friction diagram; and investigate the slip transition process from complete slip to full plastic yielding by comparing the evolutionary relationship between plasticity and slip. For the common simplification of the sliding friction model for two rough surfaces, the current study lacks the analysis of the whole sliding process for two hemispheres in the case of lateral contact, as well as the theoretical analysis of hemispheres and planes in the state of complete sliding, and the related predictions need to be supported by friction experiments, and the corresponding friction phenomena need to be analyzed by theoretical models.
This entry is adapted from the peer-reviewed paper 10.3390/mi13111907