
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Włodzimierz Makulski | + 2595 word(s) | 2595 | 2020-12-03 10:13:38 | | | |
| 2 | Bruce Ren | Meta information modification | 2595 | 2020-12-10 02:41:36 | | |
Video Upload Options
In recent years, we have seen spectacular growth in the experimental and theoretical investigations of magnetic properties of small subatomic particles: electrons, positrons, muons, and neutrinos. However, conventional methods for establishing these properties for atomic nuclei are also in progress, due to new, more sophisticated theoretical achievements and experimental results performed using modern spectroscopic devices. In this review, a brief outline of the history of experiments with nuclear magnetic moments in magnetic fields of noble gases is provided. In particular, nuclear magnetic resonance (NMR) and atomic beam magnetic resonance (ABMR) measurements are included in this text. Various aspects of NMR methodology performed in the gas phase are discussed in detail. The basic achievements of this research are reviewed, and the main features of the methods for the noble gas isotopes: 3He, 21Ne, 83Kr, 129Xe, and 131Xe are clarified. A comprehensive description of short lived isotopes of argon (Ar) and radon (Rn) measurements is included. Remarks on the theoretical calculations and future experimental intentions of nuclear magnetic moments of noble gases are also provided.
1. Introduction
The seven chemical elements known as noble (or rare gases) belong to the VIIIa (or 18th) group of the periodic table. These are: helium (2He), neon (10Ne), argon (18Ar), krypton (36Kr), xenon (54Xe), radon (86Rn), and oganesson (118Og). Their positions in the periodic table of elements are still the subject of some controversy [1]. Noble gases at normal conditions are colorless, odorless, and nonflammable monoatomic gases. The completed valence electron in the outer shell leads to this species having very low chemical activity, and they are then termed as inert gases [2]. However, several covalent and additive species of xenon are known today, mainly with strongly reducing fluorine and oxygen atoms [3]. Noble gases can be found in the Earth’s atmosphere in trace amounts: 0.00052% of helium, 0.0018% of neon, 0.93% of argon, 0.00011% of krypton, 0.0000087% of xenon, and 6 × 10−18 molar percent of radon.
Certain isotopes of noble gases possess intrinsic magnetic properties, such as a nuclear spin number (I) and as their nuclear magnetic moments (NMMs). There is no reason to doubt the importance of these parameters for the broad field of chemical and physical phenomena. The aim of this review is to show the developments of nuclear magnetic resonance (NMR) spectroscopy in the field of precisely establishing nuclear dipole moments for nuclei that belong to the group of noble gases. Experiments involving gas phase NMR achievements [4][5] are discussed in detail along with the new developments of different methods leading to measurements and theoretical calculations of the magnetic properties of noble gases.
It is clear that nuclear magnetic moments, along with the shape and size of nuclei and quadrupole moments, play an important role in discussions regarding the structure and behavior of nuclear composition. The spectacular growth of theoretical studies using different methods [6] needs more precise experimental values for the comparison and verification of results. Since the early measurements in atom-molecular beam experiments performed by I.I. Rabi et al. [7] between 1930 and 1937, NMR has played a crucial role in establishing the first magnetic moments of nuclei. Particularly, more accurate NMR results can be received when gas phase experiments are performed. The radiofrequency spectra for isolated atoms or molecules can be relatively easily measured when new, advanced NMR spectrometers are used. The calculations of diamagnetic effects, also known as shielding effects present in any atom or molecule, are crucial for precise calculations. In this case, high-level theoretical computations can be performed for a single atom at room conditions. If we join both these kinds of examinations, a full analysis of nuclear moments is possible [4][5].
It is well known that noble gas atoms have very long nuclear spin relaxation times [8]. This leads to very narrow NMR resonance lines and high digitalization of the spectra is possible. Very narrow lines are noticed even for quadrupolar nuclei due to the spherical symmetry of the electron distribution in atoms. The effect of the surface-to-volume ratio and temperature can change the relaxation times only to an extent. It is very useful that gaseous signals for different density samples can be measured with good precision.
2. Investigation of Nuclear Magnetic Moments (NMMs) by Experiment and Theory
2.1. Definition of Nuclear Magnetic Moment
The nuclear system is a complex physical structure consisting of nucleons, i.e., protons and neutrons [9]. The nuclei in atoms or molecules have several physical properties that define their behavior. These are the mass, electric charge, shape and radius, and electromagnetic moments and spin. The magnetic moment of nucleus X is expressed in the following form [10]:
|
µX = gX × µN × IX |
(1) |
where IX is the so-called spin, gX is the g nuclear factor of nucleus X, and the constant µN = e ħ /2mp (where mp is the proton mass) is known as the nuclear magneton μN = 5.05078353(13) × 10−27 J/T [11]. In an external magnetic field oriented along the axis z, a magnetic vector of nucleus with spin I may receive 2I + 1 orientations with IZ = mIħ, which are characterized by the magnetic quantum numbers mI, where –I ≤ mI ≤ I.
In experiments performed in uniform magnetic fields, only one component of the NMM can be observed in direction z of the applied field. This is often called the nuclear magnetic moment value itself. As the NMM is a vector, the full magnitude is µX(/Ix. The magnetic properties of a given nuclei can also be emphasised as the gyromagnetic ratio (magnetogyric ratio) γx. γx is the ratio of its magnetic moment to its angular momentum: γx = gx × µX/ħ in rad s−1T−1 units. When divided by the 2π factor, the gyromagnetic ratio is often used in NMR spectroscopy because of its direct proportionality to the resonance frequency of the nucleus under consideration. Several compilations of NMR frequencies in different magnetic fields expressed in induction units (B0) are well known (see e.g., Bruker Almanach).
A few theoretical models can predict the value of the magnetic dipole moment, and there are several experimental techniques aimed at carrying out measurements in nuclei within the nuclear chart. They will be presented for noble gas nuclei in the next sections of this paper.
2.2. Nuclear Magnetic Resonance (NMR) Procedure for Accurate NMM Determination
NMR spectroscopy belongs to the methods that are often used for precisely measuring the nuclear magnetic moments of different stable nuclei [12]. As NMR spectroscopy relies on the photon absorption of quantum energy that corresponds to the radio frequency region, the transition between the two states can be formulated as:
|
ΔE = h × Δν |
(2) |
where h is Planck’s constant (h = 6.62607004 × 10−34 J s). In NMR and Magnetic resonance imaging (MRI), the quantity Δν is called the resonance or the Larmor frequency. When the energy of the photon matches the energy difference between the two spin states, an absorption of energy occurs. The resonance frequency vX for nucleus X in the isotropic medium is proportional to the external magnetic field induction Bz :
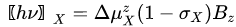 |
(3) |
where is the transition-related change of the projection of the magnetic moment on the z field axis, and σX is the shielding parameter. An analogous equation can be written for the other nuclei placed in the same magnetic field:
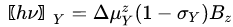 |
(4) |
A precise solution of Equations (3) and (4) is difficult as the measuring of magnetic fields is usually a complicated task. Thus, it is convenient to divide both equations by pages, eliminating the external magnetic field induction Bz, and to use the final formula crucial for establishing the NMM using NMR spectroscopy:
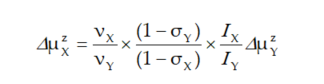 |
(5) |
This relationship is a rule for the measurements of many NMM also discussed in this paper.
2.3. Gas-Phase Measurements of NMR Frequencies
It is very profitable to perform experiments in the gas phase. Typically, gaseous samples are prepared in the glass vacuum line equipped with a pump, cold traps, and a pressure gauge. Samples are filled with pure gases by condensation in liquid nitrogen or liquid helium temperatures and sealed under a vacuum by a torch. These gas ampoules are fitted into the thin-walled NMR tubes with liquid deuterated solvents in the annular space for use the lock system. In this way, prepared test tubes, after checking its strength, can be measured in most NMR spectrometers, such as conventional liquid samples.
Any given property of a gaseous state in equilibrium can be conveniently expressed as the virial expansion of a power series of the density number [13]. The virial coefficients characterize the isolated molecule ν0(nX) and the intermolecular interactions νAB(nX) between gaseous ingredients at a given temperature. Frequencies extrapolated to the zero-pressure limit are commonly used in this case:
|
ν(nX) = ν0(nX) + νAA(nX)ρA + νAB(nX)ρB + …. |
(6) |
where ρA and ρB are the densities of A and B gaseous substances. The virial coefficients νAA and νAB depend on the bulk susceptibility corrections and on the terms involving the intermolecular interactions, which take place during collisions. The amount of A is usually maintained at very low concentrations, and the temperature is kept constant. The above equation can therefore be formulated in a simpler fashion:
|
ν(nX) = ν0(nX) + νAB(nX)ρB |
(7) |
Analogously, the magnetic shielding parameter σ(X) can be written as a simple concentration (density) function; and the equation is valid when chemical shifts δ (ppm) or nuclear magnetic shielding σ (ppm) are analyzed as pressure (density) functions:
|
σ(X) = σo(X) + σAB(X) ρB |
(8) |
where σo(X) is the chemical shielding of the X nucleus in the isolated molecule or atom, and σAB means the second virial coefficient of chemical shielding. The σAB term is due to bimolecular collisions involving several specific interactions and the bulk susceptibility effect of the gas. At moderate densities, the influence of three-body and high-order collisions can be neglected. In gaseous phases, linear dependencies (7) and (8) are observed up to pressures of ~40 atm [14] where only interactions of two bodies occur. Extrapolation of the shielding values to the zero density limit provides the so, parameter, which is free from intermolecular interactions. It is important to use at least two different gaseous solvents to test the final result of σo(X); within the limit of experimental error every solvent should give the same value. The σo(X) constants may be directly compared with the results of quantum chemical calculations for a single molecule or atom in a vacuum (at the temperature of the experiment).
2.4. Diamagnetic Corrections
In the NMR experiment, we can measure the NMM disturbed by the influence of the electron density in the given molecule or atom. These systematic effects, often known as diamagnetic corrections, are expressed as shielding constants σx (see Equations (3)–(5)). They describe the magnetic polarization of the medium by an external field. The more accurate corrections are, therefore, necessary to extract the NMM for the bare nuclei. The aforementioned factors should be involved for the reference nucleus and given nucleus under study. Since the first magnetism theories, these correction factors have been called diamagnetic factors. In our case, the diamagnetic factor is a multiplier in Equation (5) defined by means of:
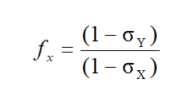 |
(9) |
where σx,y are the shielding of nuclei X and Y, belonging to the reference nucleus and that under consideration. The shielding factors should be expressed on the absolute scale in ppm units. In this case, the diamagnetic shielding factor can appear as close to 1. The fx factors are shown in tables presented in the next paragraphs. In practice, the correction factor of diamagnetic shielding can even be as large as ~14,000 ppm for 185Re and 187Re, which results in a dipole magnetic moment correction of ~3 × 10−2 μN [15]. On the other hand, these corrections in the proton case are of the order 3 × 10−5 ppm. We can suppose that correction factors for a particular noble gas will be of varying importance. The numerical corrections are shown in Table 8, and a short discussion about this problem can be found in the Summary and Prospect part of this paper.
2.5. Direct Measurements of Shielding Constants
A considerable effort has been made to establish the so-called absolute shielding scales for individual active nuclei (e.g., see [15][16]). Generally, good shielding scales are known for 1H [17] and a few light nuclei [18][19]. The worse situations concern heavy nuclei where strong relativistic effects are present. The theoretical calculations of these effects have only been used in the last decade, and a relatively limited quantity of relativistic data has been known up to now. The validity of the shielding corrections rises when atomic numbers increase for the given nuclei. This means that the NMM of heavy isotopes are given with much less accuracy than for light nuclei.
2.6. Other Methods
Several physico-chemical techniques can serve as a source of NMM values: microwave spectroscopy, atomic and molecular beam experiments, optical spectroscopy, optical double resonance and pumping techniques, Mössbauer spectroscopy, nuclear orientation, specific heat measurements, and dynamic nuclear self-polarization. Among them, the atomic and molecular beam resonance methods (ABMR) have played a main role when the NMM of stable nuclei are of interest [20][21]. ABMR is a method related to the well-known NMR spectroscopy technique. Several variations of this approach exist. Atomic or molecular beams are generated in a vacuum line by heating samples to a high temperature. The beams are then formatted in the high vacuum apparatus where two magnets create inhomogeneous magnetic fields to influence the trajectories of particles before going to the detector. A strong magnetic oscillation field gradient was used to flip the magnetic moment of particles. The selection of quantum states connected with spin magnetic moments through space quantization can give a characteristic pattern of resonance lines. If the resonance condition is fulfilled:
|
ωR = γ/ħ × BR |
(10) |
the spin is now precessing around the BR direction with an angular frequency known as the Rabi frequency ωR. The precession rate is independent of the spatial distribution of the spins. The Rabi method was capable of detecting the magnetic resonance absorption spectra and estimating nuclear magnetic moments of several nuclei, among them protons, deuterium, and heavier nuclei [22]. The concept of the ABMR method in the more sophisticated variations can also be used for studying short-lived radioactive nuclei (isotopes with a half-life shorter than 1 min) and metastable states (a life-time of at least a few milliseconds). It is very beneficial when the NMM of nucleus is known from ABMR and NMR methods at the same time because of the possibility of comparing both results for different chemical species and verifying shielding constants and magnetic moments together (see for example [23]).
Many NMMs of short lived nuclides were measured by Collinear Fast Beam Laser Spectroscopy (CFBLS, CLS), Optical Pumping (OP) with Radiative Detection and β-NMR experiments. The CFBLS method is a kind of high resolution laser spectroscopy for investigations of short-lived isotopes in their ground-states. This method was developed by Kaufman [24]. CLS can not only investigate nuclear magnetic moments but also different nuclear properties, such as nuclear charge radii [25]. β-NMR is a general method suited to many fields of research and can measure shifts in the Larmor frequency and relaxation times. The spectroscopic NMR signal is observed as the anisotropic emission of β-particles. It can be prepared for application to the short-lived β decaying nuclei that are delivered as a beam species. Because of the former nuclei hyperpolarization, this method has a sensitivity of even five orders of magnitude more than that of a normal NMR experiment [26][27]. Several examples of these methods of research will be presented in relation to 17Ne˗27Ne, 33Ar˗43Ar, and 203Rn˗225Rn nuclei in the following sections.
The experimental results of NMM measurements for stable isotopes of noble gases performed so far by ABMR and NMR methods were collected in the series of tables. The original results of individual measurements were recalculated using the new, best quality physical quantities and then included in the data charts.The final results are not identical to the author’s primary, original findings.
References
- Grochala, W. On the position of helium and neon in the Periodic Table of Elements. Found. Chem. 2018, 20, 191–207, doi:10.1007/s10698-017-9302-7.
- Schrobilgen, G.J. Noble gas. In Encyclopedia Britannica; Encyclopedia Britannica Inc.: Chicago, IL, USA, 2019. Available online: https://www.britannica.com/science/noble-gas (accessed on 23 October 2020).
- Grochala, W.; Khriachtchev, L.; Räsänen, M. Noble-gas chemistry. In Physics and Chemistry at Low Temperatures, 1st ed.; Khriachtchev, L., Ed.; Taylor &Francis: New York, NY, USA, 2011; Chapter 13, pp. 419–446; doi:10.1201/9780429066276.
- Antušek, A.; Jackowski, K.; Jaszuński, M.; Makulski, W.; Wilczek, M. Nuclear magnetic dipole moments from NMR spectra. Chem. Phys. Lett. 2005, 411, 111–116, doi:10.1016/j.cplett.2005.06022.
- Jaszuński, M.; Antušek, A.; Garbacz, P.; Jackowski, K.; Makulski, W.; Wilczek, M. The determination of accurate nuclear magnetic dipole moments and direct measurement of NMR shielding constans. Prog. Nucl. Magn. Reson. Spectrosc. 2012, 67, 49–63, doi:10.1016/j.pnmrs.2012.03.002.
- Zhao, E. Recent progress in theoretical studies of nuclear magnetic moments. Chin. Sci. Bull. 2012, 57, 4394–4399, doi:10.1007/s11434-012-5491-6.
- Forman, P. Molecular beam measurements of nuclear moments before magnetic resonance. Ann. Sci., 1998, 55, 111–160, doi:10.1080/00033799800200141.
- Jameson, C.J. The Noble Gases. In Multinuclear NMR; Mason, L., Ed.; Springer: Boston, MA, USA, 1987; Chapter 18, pp. 463–477; doi:10.1007/978-1-4613-1783-8.
- Jevremović, T. Nuclear Theory. In Nuclear Principles in Engineering; Springer: Boston, MA, USA, 2005; Chapter 3, pp. 61–126; doi:10.1007/b101136.
- Keeler, J. Understanding NMR Spectroscopy, 2nd ed.; John Wiley & Sons: Chichester, UK, 2010; ISBN 978-0-470-74609-7.
- Mohr, P.J.; Newell, D.B.; Taylor, B.N. CODATA Recommended Values of the Fundamental Physical Constants: 2014. Rev. Mod. Phys. 2016, 88, 035009-1–035009-11, doi:10.1103/RevModPhys.88.035009.
- Jaszuński, M.; Jackowski, K. Nuclear Magnetic Dipole Moments from NMR Spectra—Quantum Chemistry and Experiment. In Precision Physics of Simple Atoms and Molecules; Karshenboim, S.G., Ed.; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2008; Volume 745, pp. 233–260; doi:10.1007/978-3-540-75479-4_13.
- Dymond, J.D.; Marsh, K.N.; Wilhoit, R.C. Virial Coefficients of Pure Gases and Mixtures; Fenkel, M., Marsch, K.N., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; ISBN 978-3-540-44340-7.
- Jameson, C.J. Effects of Intermolecular Interactions and Intramolecular Dynamics on Nuclear Resonance. Bull. Magn. Reson. 1981, 3, 3–28.
- Antušek, A.; Repisky, M. NMR absolute shielding scales and nuclear magnetic dipole moments of transition metal nuclei. Phys. Chem. Chem. Phys. 2020, 22, 7065–7076, doi:10.1039/d0cp00115e.
- Jameson, C.J. Chemical Shift Scales on an Absolute Basis; eMagRes; John Wiley & Sons: Hoboken, NJ, USA, 2011; doi:10.1002/9780470034590.emrstm0072.pub2.
- Garbacz, P.; Jackowski, K.; Makulski, W.; Wasylishen, R.E. Nuclear Magnetic Shielding for Hydrogen in Selected Isolated Molecules. J. Phys.Chem. A 2012, 116, 11896–11904, doi:10.1021/jp309820v.
- Jackowski, K.; Makulski, W.; Szyprowska, A.; Antušek, A.; Jaszuński, M.; Jusélius, J. NMR shielding constants in BF3 and magnetic dipole moments of 10B and 11B nuclei. J. Chem. Phys. 2009, 130, 044309-1–044309-5, doi:10.1063/1.3065670.
- Makulski, W.; Szyprowska, A.; Jackowski, K. Precise determination of the 13C nuclear magnetic moment from 13C, 3He and 1H NMR measurements in the gas phase. Chem. Phys. Lett. 2011, 511, 224–228, doi:10.1016/j.cplett.2011.06.065.
- Nierenberg, W.A. Atomic beam magnetic resonance. Physica 1967, 33, 18–28, doi:10.1016/0031-8914(67)90258-3.
- Penselin, S. Recent Developments and Results of the Atomic-Beam Magnetic-Resonance Method. In Progress in Atomic Spectroscopy: Physics of Atoms and Molecules; Hanle, W., Kleinpoppen, H., Eds.; Springer: Boston, MA, USA, 1978; pp. 463–490; doi:10.1007/978-1-4615-7688-4_10.
- Kellogg, J.M.B.; Rabi, I.I.; Ramsey, N.F., Jr.; Zacharias, J.R. The Magnetic Moments of the Proton and the Deuteron. The Radiofrequency Spectrum of H2 in Various Magnetic Fields. Phys. Rev. 1939, 56, 728, doi:10.1103/PhysRev.56.728.
- Makulski, W. The radiofrequency NMR spectra of lithium salts in water; Reevaluation of Nuclear Magnetic Moments for 6Li and 7Li nuclei. Magnetochemistry 2018, 4, 9, doi:10.3390/magnetochemistry4010009.
- Kaufman, S.L. High-resolution laser spectroscopy in fast beams. Opt. Commun. 1976, 17, 309–312, doi:10.1016/0030-4018(76)90267-4.
- Geithner, W.; Georg, U.; Kappertz, S.; Keim, M.; Klein, A.; Lievens, P.; Neugart, R.; Neuroth, M.; Vermeeren, L.; Wilbert, S. Measurement of nuclear moments and radii by collinear laser spectroscopy and by β-NMR spectroscopy. Hyperfine Interact. 2000, 129, 271–288, doi:10.1023/A:1012642707147.
- Mihara, M. Fundamentals of β-NMR and its New Developments in Materials Science Studies. Hyomen Kagaku 2017, 38, 188–193, doi:10.1380/jsssj.38.188.
- Abov, Yu. G.; Gulko, A.D.; Dzheparov, F.S. Beta-NMR spectroscopy: Modern state and prospects. Phys. At. Nucl. 2006, 69, 1701–1710, doi:10.1134/S106377880610005X.




