1. Mathematical Definition

A propagation graph is a simple directed graph [math]\displaystyle{ \mathcal G = (\mathcal V, \mathcal E) }[/math] with vertex set [math]\displaystyle{ \mathcal V }[/math] and edge set [math]\displaystyle{ \mathcal E }[/math].

The vertices models objects in the propagation scenario. The vertex set [math]\displaystyle{ \mathcal V }[/math] is split into three disjoint sets as [math]\displaystyle{ \mathcal V = \mathcal V_t \cup \mathcal V_r \cup\mathcal V_s }[/math] where [math]\displaystyle{ \mathcal V_t }[/math] is the set of transmitters, [math]\displaystyle{ \mathcal V_r }[/math] is the set of receivers and [math]\displaystyle{ \mathcal V_s }[/math] is the set of objects named "scatterers".

The edge set [math]\displaystyle{ \mathcal E }[/math] models the propagation models propagation conditions between vertices. Since [math]\displaystyle{ \mathcal G }[/math] is assumed simple, [math]\displaystyle{ \mathcal E \subset \mathcal V^2 }[/math] and an edge may be identified by a pair of vertices as [math]\displaystyle{ e = (v,v') }[/math] An edge [math]\displaystyle{ e = (v,v') }[/math] is included in [math]\displaystyle{ \mathcal E }[/math] if a signal emitted by vertex [math]\displaystyle{ v }[/math] can propagate to [math]\displaystyle{ v' }[/math]. In a propagation graph, transmitters cannot have incoming edges and receivers cannot have outgoing edges.

Two propagation rules are assumed

• A vertex sums the signals impinging via its ingoing edges and remits a scaled version it via the outgoing edges.
• Each edge [math]\displaystyle{ e=(v,v') }[/math] transfers the signal from [math]\displaystyle{ v }[/math] to [math]\displaystyle{ v' }[/math] scaled by a transfer function.

The definition of the vertex gain scaling and the edge transfer functions can be adapted to accommodate particular scenarios and should be defined in order to use the model in simulations. A variety of such definitions have been considered for different propagation graph models in the published literature.

Vector signal flow graph of a propagation graph. https://handwiki.org/wiki/index.php?curid=1456284

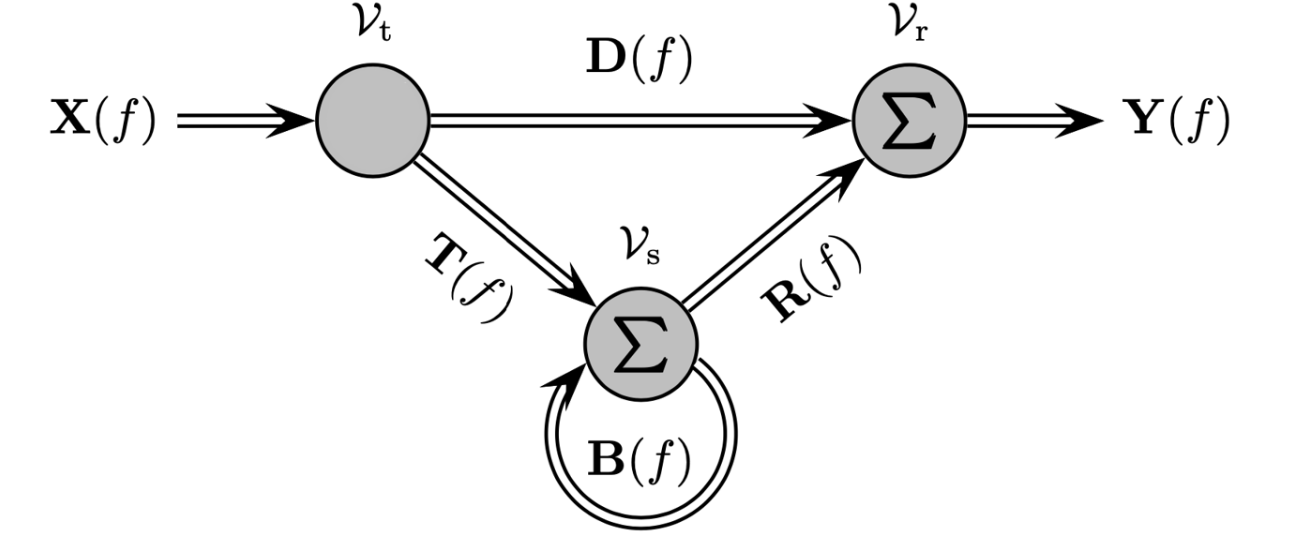
The edge transfer functions (in the Fourier domain) can be grouped into transfer matrices as

• [math]\displaystyle{ \mathbf D(f) }[/math] the direct propagation from transmitters to receivers
• [math]\displaystyle{ \mathbf T(f) }[/math] transmitters to scatterers
• [math]\displaystyle{ \mathbf R(f) }[/math] scatterers to receivers
• [math]\displaystyle{ \mathbf B(f) }[/math] scatterers to scatterers,

where [math]\displaystyle{ f }[/math] is the frequency variable.

Denoting the Fourier transform of the transmitted signal by [math]\displaystyle{ \mathbf X(f) }[/math], the received signal reads in the frequency domain [math]\displaystyle{ \mathbf Y (f) = \mathbf D(f) \mathbf X (f) + \mathbf R (f)\mathbf T (f) \mathbf X (f) + \mathbf R (f)\mathbf B(f) \mathbf T (f) \mathbf X (f) +\mathbf R (f)\mathbf B^2(f) \mathbf T (f) \mathbf X (f) + \cdots }[/math]

2. Transfer Function

The transfer function [math]\displaystyle{ \mathbf H(f) }[/math] of a propagation graph forms an infinite series^[1] [math]\displaystyle{ \begin{align} \mathbf H(f) &= \mathbf D(f)+ \mathbf R (f)[ \mathbf I+ \mathbf B(f) + \mathbf B(f)^{2} + \cdots ] \mathbf T (f)\\ &= \mathbf D(f)+ \mathbf R (f) \sum_{k=0}^\infty \mathbf B(f)^k \mathbf T(f) \end{align} }[/math] The transfer function is a Neumann series of operators. Alternatively, it can be viewed pointwise in frequency as a geometric series of matrices. This observation yields a closed form expression for the transfer function as [math]\displaystyle{ \mathbf H(f) = \mathbf D(f) + \mathbf R(f) [\mathbf I - \mathbf B(f)]^{-1} \mathbf T(f),\qquad \rho(\mathbf B(f))\lt 1 }[/math] where [math]\displaystyle{ \mathbf I }[/math] denotes the identity matrix and [math]\displaystyle{ \rho(\cdot) }[/math] is the spectral radius of the matrix given as argument. The transfer function account for propagation paths irrespective of the number of 'bounces'.

The series is similar to the Born series from multiple scattering theory^[2].

The impulse respones [math]\displaystyle{ \mathbf h(\tau) }[/math] are obtained by inverse Fourier transform of [math]\displaystyle{ \mathbf H(f) }[/math]

2.1. Partial Transfer Function

Closed form expressions are available for partial sums, i.e. by considering only some of the terms in the transfer function. The partial transfer function for signal components propagation via at least [math]\displaystyle{ K }[/math] and at most [math]\displaystyle{ L }[/math] interactions is defined as [math]\displaystyle{ \mathbf H_{K:L}(f) = \sum_{k=K}^{L} \mathbf H_k(f) }[/math] where [math]\displaystyle{ \mathbf H_k(f) = \begin{cases} \mathbf D(f),& k=0\\ \mathbf R(f) \mathbf B^{k-1}(f) \mathbf T(f), & k = 1,2,3,\ldots \end{cases} }[/math] Here [math]\displaystyle{ k }[/math] denotes the number of interactions or the bouncing order.

Animation of power delay profiles calculated from partial transfer functions of a propagation graph model. The red line indicates the delay of the direct path. https://handwiki.org/wiki/index.php?curid=1130110

The partial transfer function is then^[1] [math]\displaystyle{ \mathbf H_{K:L}(f) = \begin{cases} \mathbf D(f) + \mathbf R(f) [\mathbf I-\mathbf B^L(f)] \cdot [\mathbf I-\mathbf B(f)]^{-1} \cdot \mathbf T(f), & K = 0\\ \mathbf R(f) [\mathbf B^{K-1}(f)-\mathbf B^L(f)] \cdot [\mathbf I-\mathbf B(f)]^{-1} \cdot \mathbf T(f), & \text{otherwise}.\\ \end{cases} }[/math] Special cases:

• [math]\displaystyle{ \mathbf H_{0:\infty}(f) = \mathbf H(f) }[/math]: Full transfer function.
• [math]\displaystyle{ \mathbf H_{1:\infty}(f) = \mathbf R(f) [\mathbf I-\mathbf B(f)]^{-1} \mathbf T(f) }[/math]: Inderect term only.
• [math]\displaystyle{ \mathbf H_{0:L}(f) }[/math]: Only terms with [math]\displaystyle{ L }[/math] or fewer bounces are kept ([math]\displaystyle{ L }[/math]-bounce truncation).
• [math]\displaystyle{ \mathbf H_{L+1:\infty}(f) }[/math]: Error term due to an [math]\displaystyle{ L }[/math]-bounce truncation.

One application of partial transfer functions is in hybrid models, where propagation graphs are employed to model part of the response (usually the higher-order interactions).

The partial impulse responses [math]\displaystyle{ \mathbf h_{K:L}(\tau) }[/math] are obtained from [math]\displaystyle{ \mathbf H_{K:L}(f) }[/math] by the inverse Fourier transform.

3. Propagation Graph Models

The propagation graph methodology have been applied in various settings to create radio channel models. Such a model is referred to as a propagation graph model. Such models have been derived for scenarios including

• Unipolarized inroom channels. The initial propagation graph models ^[1][3][4] were derived for unipolarized inroom channels.
• In ^[5] a polarimetric propagation graph model is developed for the inroom propagation scenario.
• The propagation graph framework has been extended in ^[6] to time-variant scenarios (such as the vehicle-to-vehicle). For terrestrial communications, where relative velocity of objects are limited, the channel may be assumed quasi-static and the static model may be applied at each time step.
• In a number of works including ^{[7][8][9][10]} propagation graphs have been integrated into ray-tracing models to enable simulation of reverberation phenomena. Such models are referred to as hybrid models.
• Complex environments including outdoor-to-indoor cases.^[11] can be studied by taking advantage of the special structure of propagation graphs for these scenarios. Computation methods for obtaining responses for very complex environments have been developed in ^[12]
• The graph model methodology has been used to make spatially consistent MIMO channel models.^[13]
• Several propagation graph models have been published for high-speed train communications.^[14][15]

4. Calibration of Propagation Graph Models

To calibrate a propagation graph model, its parameters should be set to reasonable values. Different approaches can be taken. Certain parameters can be derived from simplified geometry of the room. In particular, reverberation time can be computed via room electromagnetics. Alternatively, the parameters can ben set according to measurement data using inference techniques such as Method of moments (statistics) ^[5], Approximate Bayesian Computation.^[16], or Deep neural networks ^[17]

5. Related Radio Channel Model Types

The method of propagation graph modeling is related to other methods. Noticeably,

• Multiple Scattering Theory Multiple scattering theory
• Radiosity Radiosity (computer graphics)
• Ray tracing Ray tracing
• Geometry Based Stochastic Channel Models (GBSCM)