Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Gbolahan Joseph Adekoya
 -- 1444 2022-10-17 12:33:56 |
2 format correct
Vivi Li
 + 37 word(s) 1481 2022-10-18 03:52:51 |

Video Upload Options

We provide professional Video Production Services to translate complex research into visually appealing presentations. Would you like to try it?
No, upload directly Yes

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Adekoya, O.C.;  Adekoya, G.J.;  Sadiku, E.R.;  Hamam, Y.;  Ray, S.S. DFT Calculations in Designing Polymer-Based Drug Delivery Systems. Encyclopedia. Available online: https://encyclopedia.pub/entry/29703 (accessed on 25 December 2024).
Adekoya OC,  Adekoya GJ,  Sadiku ER,  Hamam Y,  Ray SS. DFT Calculations in Designing Polymer-Based Drug Delivery Systems. Encyclopedia. Available at: https://encyclopedia.pub/entry/29703. Accessed December 25, 2024.
Adekoya, Oluwasegun Chijioke, Gbolahan Joseph Adekoya, Emmanuel Rotimi Sadiku, Yskandar Hamam, Suprakas Sinha Ray. "DFT Calculations in Designing Polymer-Based Drug Delivery Systems" Encyclopedia, https://encyclopedia.pub/entry/29703 (accessed December 25, 2024).
Adekoya, O.C.,  Adekoya, G.J.,  Sadiku, E.R.,  Hamam, Y., & Ray, S.S. (2022, October 17). DFT Calculations in Designing Polymer-Based Drug Delivery Systems. In Encyclopedia. https://encyclopedia.pub/entry/29703
Adekoya, Oluwasegun Chijioke, et al. "DFT Calculations in Designing Polymer-Based Drug Delivery Systems." Encyclopedia. Web. 17 October, 2022.
DFT Calculations in Designing Polymer-Based Drug Delivery Systems
Edit
This entry is adapted from the peer-reviewed paper 10.3390/pharmaceutics14091972

Drug delivery systems transfer medications to target locations throughout the body. These systems are often made up of biodegradable and bioabsorbable polymers acting as delivery components. The introduction of density functional theory (DFT) has tremendously aided the application of computational material science in the design and development of drug delivery materials. The use of DFT and other computational approaches avoids time-consuming empirical processes.

drug delivery system DFT polymer nanocomposites quantum mechanics

1. Introduction

One of the most exciting areas of biomedical research is the investigation of innovative drug delivery methods. To improve medication cell/tissue selectivity, rate of release, therapeutic index, and bioavailability, multidisciplinary scientific techniques integrating traditional or engineered technologies are applied. The building elements of these systems are typically biodegradable and bioabsorbable polymers, with their copolymers serving as delivery components [1][2]. To boost the therapeutic efficiency of medications, therapeutic agents, and vaccines, drug delivery systems are used to transport them to a specific location within the body with a regulated release [3]. Computational methodologies, such as DFT, have been developed to bypass time-consuming empirical procedures for the optimization of these formulations.
Density functional theory (DFT) computations, in particular, offer outstanding levels of accuracy with comparable computation time and are more inexpensive in terms of computational resources than other ab initio approaches currently in use. Additionally, it avoids the many-electron wavefunction in favour of electron density and has the potential benefit of dealing with only one function of a single spatial coordinate. Moreover, it employs generalized gradient approximations (GGAs), which use the density gradient to generate a more precise function [4][5][6].
DFT are a strong and low-cost method for revealing a material’s fundamental information, including energy, geometric structure, electrical, and optical characteristics. It offers important theoretical predictions and assistance from the standpoint of material design. It provides crucial information at the levels of atoms, molecules, and unit cells from the perspective of interpreting the results. The influence of element doping on the geometric and electrical characteristics of polymer-based drug carriers, as well as the interaction between the drugs and the nanocarriers, is considerably aided by DFT calculations [7][8].
For example, Kazemi and colleagues used DFT calculations to examine the hydrogen bonding interactions between letrozole and methacrylic acid-trimethylolpropane trimethacrylate copolymers as drug delivery systems [9]. Meanwhile, Karatars and co-workers investigated the interaction of curcumin with a poly(lactic-co-glycolic acid) and montmorillonite composite in a drug delivery system from the first principle calculation [10]. The drug delivery potential of hexagonal boron nitride (h-BN) and PEGylated h-BN (PEG-h-BN) for the delivery of the anticancer medication Gemcitabine (Gem) were investigated by Farzaneh and colleagues using DFT simulations. With adsorption energy of -15.08 kJ/mol, the drug physically adsorbs into the h-BN surface by the growth of π-π stacking. The findings also show that the PEG group grafting to h-BN resulted in π-π stacking, which is enhanced by the generation of strong hydrogen bonds and resulted in a 20% increase in adsorption energy (−90.74 kJ/mol) [11].

2. DFT: A Quick Overview

The first-principles approach is based on quantum mechanics (QM), which expresses the conduction of electrons and atomic nuclei in every condition. The basic equation in this computation is the Schrödinger equation (Equation (1)). The many-body problem occurs in many-electron systems when electrons interact with one another [12][13][14].
Ĥ Ψ = E Ψ
where Ψ is the wavefunction, Ĥ is Hamiltonian, and E is the system’s energy.
Several approximations, such as the Born–Oppenheimer approximation, were devised to solve the complex Schrödinger equation. Two theorems proposed by Hohenberg and Kohn served as the foundations of DFT. The Hohenburg–Kohn equation may be written as Equation (2) according to the first theorem.
E 0 = E v [ ρ 0 ] = T ¯ [ ρ 0 ] + v ¯ e e [ ρ 0 ] + ∫ ρ 0 ( ɍ ) v ( d ɍ ) d ɍ
where T¯ is the sum of electronic kinetic energy, ν(ɍ) is the function for nuclear potential energy for an electron at a point ɍ, v¯ is electron–electron repulsion, and the overbars denote the average variables.
The second hypothesis proposes a density minimum principle, stating that the ground state energy of any trial electron density (ρtr) cannot be lower than that of the true ground system and may be represented by Equation (3).
E v [ ρ t r ] = E v ≥ E 0 = [ ρ 0 ]
he electronic density n(ɍ) is defined by fulfilling the requirement that n(ɍ) d ɍ is the probability of finding any electron in the volume d3ɍ around ɍ. It is simply |ϕ(ɍ)|2 for a single electron with wavefunction ϕ(ɍ). In DFT, researchers represent the ground-state energy in terms of n(ɍ) instead of Ψ [15][16].
F [ n ] = min Ψ → n 〈 Ψ | { T ¯ + ν ¯ e e   } | Ψ 〉
Moreover, the Kohn–Sham technique is a method for calculating atom and molecule energy, structure, and characteristics [17][18].
E v [ ρ ] = ∫ ρ ( ɍ ) v ( d ɍ ) d ɍ + T ¯ s [ ρ ] + 1 2 ∬ ρ ( ɍ 1 ) ρ ( ɍ 2 ) ɍ 12 d ɍ 1 d ɍ 2 + E X C [ ρ ]
EXC stands for exchange-correlation (XC) energy, which consists of correlation, exchange, columbic correlation, and self-interaction correction. To determine the electronic structural characteristics of polymer-based drug delivery systems, the DFT method has been widely employed. The traditional DFT approach, which uses LDA and GGA exchange-correlation (XC) functionals, produces a band gap that is underestimated. Several approximations such as DFT+U, DMFT, hybrid functionals (B3LYP, PBE0, and HSE), GW approximation, etc., have been proposed to attain better results. Although hybrid functionals and GW give a more exact value of band gap, they come at a hefty computational expense.
The materials science community has access to several DFT codes. The programs are based on various potentials, basis sets, exchange-correlation functionals, and Schrödinger equation-solving techniques. ABINIT, ADF, CASTEP, DMol3, ONETEP, Gaussian, and GAMESS are some examples of DFT programs. Table 1 summarizes the different DFT-based software, the functionals, and the basis set used in polymer-based drug delivery systems.
Table 1. Calculations in polymer-based drug delivery systems using DFT software applications.
Polymeric Carrier Drug/Therapeutic Agent DFT Code DFT Functional/Basis Set Ref.
Polylactic-co-glycolic acid and montmorillonite Curcumin COSMO module of TURBOMOLE V6.1 B97-D/TZVP [10]
Disulfur-bridged polyethyleneglycol/DOX nanoparticles Chlorin e6 (Ce6) Jaguar module in Schrödinger M06-2x/6-311(d,p)
method		 [19]
Hyaluronic acid and Zr-based porphyrinic MOF (HA-PCN-224) Doxorubicin DMol3 program PBE/DNP 4.4 [20]
polymer membranes (PDMS, PVA, PUI, PTMG-650-MDI-AP, PPG-725-MDI-AP, PCL-1250-MDI-AP) Pure liquid solvents Dmol3 module in Accelrys Materials Studio GGA/VWN-BP/DNP v4.0.0 [21]
PEG-h-BN Gemcitabine GEM GaussView software, Gaussian 09 package M06e2X/
6-31G(d,p)		 [11]
Methacrylic acid-trimethylolpropane trimethacrylate copolymers Letrozole Gaussian-98 B3LYP and B3PW91 levels/
6-31G(d)		 [9]
Acrylamide-base hydrogel Antimalarial (chloroquine, primaquine, and amodiaquine) - wb97xd/6-31++G(d,p) [22]
Chitosan, silicon dioxide, and graphene oxide Cisplatin Gaussian 09 B3LYP/LANL2DZ [23]
Graphene oxide/polyethylene glycol Sumatriptan Gaussian B3LYP/6-31+G(d) [24]
Polylactic-co-glycolic acid Anti-cancer sgents of thiazoline Gaussian 03 B3LYP/6-31G(d) [25]
Folate functionalized poly(styrene-alt-maleic anhydride), PSMA   Gaussian 09 B3LYP/6-31G(d,p) [26]
Polyheterocycles Antischistosomiasis (praziquantel, niclosamide ethanolamine salt, niclosamide, and trichlorfon) - B3LYP [27]
Poly-carboxylic acids functionalized chitosan Cisplatin Gaussview 05. - [28]
PEGylated fluorinated graphene Camptothecin (CPT) and doxorubicin
(DOX)		   - [29]
Chitosan nanocomposite Ifosfamide anticancer COMPASS - [30]
Polyester dendrimers Ibuprofen Gaussian 09 W M06-2X/6-31G(d) [31]
Polyamidoamine (PAMAM) and polyester dendrimers Favipiravir - M06-2X/6-31G(d) [32]
Hyperbranched polysiloxane containing
β-cyclodextrin		 Ibuprofen - B3LYP/6-31G(d) [33]
chitosan Nucleobase (DNA/RNA) - B3LYP/6-31++G(d,p) [34]
Poly(O-vinyl carbamate-alt-sulfones) Mucosal drug (Rhodamine B) - B3LYP, 6-311++G-
(d,p)		 [35]
PAMAM dendrimers 5-Fluorouracil Gaussian 09 B3LYP/6-31G(d,p) and M06-2X/6-31G(d,p) [36]
Chitosan nanoparticle Hydroxyurea Gaussian 09 B3LYP/6-31G(d,p) and M06-2X/6-31G(d,p) [37]
Polyethylene glycol-based nanocomposite Cephalexin DMol3 B3LYP [4]

3. Fundamental Properties of Polymer-Based Drug Delivery Systems

DFT computations may be used to derive several characteristics of polymer-based drug delivery systems [11]. To obtain the desired feature under examination, researchers might use a variety of strategies. However, Figure 1 presents a common procedure for applying DFT calculations. The creation of the drug’s and excipient polymer’s molecular structures often marks the beginning of the procedure [38][39]. Additionally, these structures may be imported from both public and commercial molecular structure databases, including the Protein Data Bank [40], PubChem Structure [41][42], and databases for polymer materials. The energy of each particular molecular structure can then be reduced by performing an initial structural relaxation. This enables the drug’s binding energy to be computed when an adsorption calculation is run to determine the most thermodynamically advantageous adsorption sites. On the other hand, interaction energy will be calculated when an adsorption calculation is performed without first optimizing the structure. Ground state calculations are used to further relax the drug-polymer combination that has formed. The generated complex may then be utilized to forecast excited state attributes, such as UV, IR, and using frequency calculations. The optimized complex’s total energy may be determined to examine the thermodynamic properties. The energy gap and molecular orbital characteristics of the drug-polymer configurations can be predicted using electronic simulations in the interim [43]. The many DFT computed characteristics of drug delivery systems based on polymers are explored in the following paragraphs.
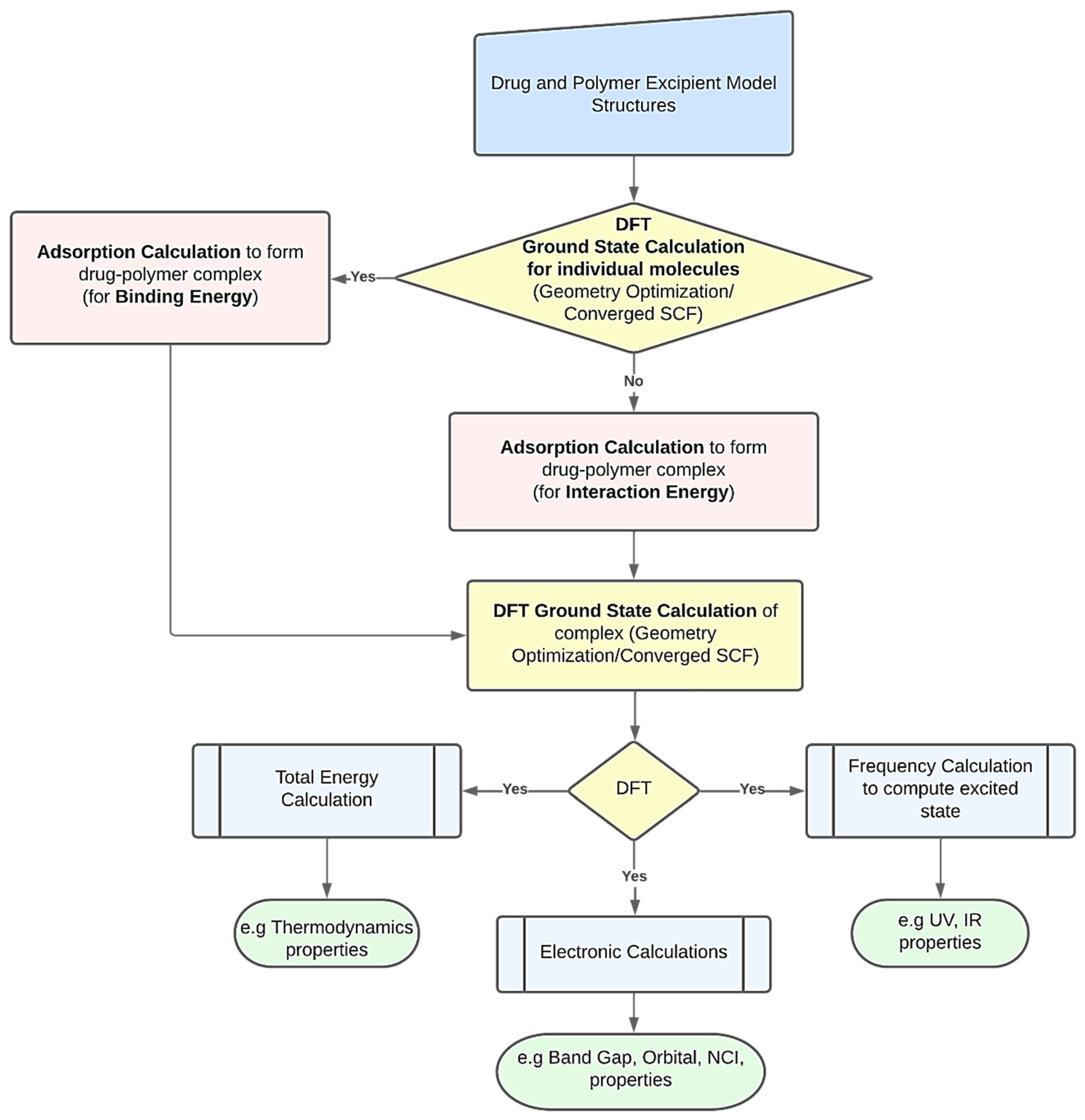
Figure 1. A schematic workflow for employing DFT calculations in polymer-based drug delivery systems.

References

  1. Adekoya, O.C.; Yibowei, M.E.; Adekoya, G.J.; Sadiku, E.R.; Hamam, Y.; Ray, S.S. A mini-review on the application of machine learning in polymer nanogels for drug delivery. Mater. Today Proc. 2022, 62, S141–S144.
  2. Procopio, A.; Lagreca, E.; Jamaledin, R.; La Manna, S.; Corrado, B.; Di Natale, C.; Onesto, V. Recent Fabrication Methods to Produce Polymer-Based Drug Delivery Matrices (Experimental and In Silico Approaches). Pharmaceutics 2022, 14, 872.
  3. Adekoya, G.J.; Rotimi Sadiku, E.; Hamam, Y.; Ray, S.S.; Esezobor, E.D.; Bolasodun, B.; Mwakikunga, W.B.; Adekoya, O.C.; Olajide, J.L.; Folorunso, O.; et al. Biodegradable Antibiotic Importers in Medicine. In Antibiotic Materials in Healthcare; Kokkarachedu, V., Kanikireddy, V., Sadiku, R., Eds.; Academic Press: Cambridge, MA, USA, 2020; Chapter 5; pp. 65–92.
  4. Adekoya, O.C.; Adekoya, G.J.; Sadiku, R.E.; Hamam, Y.; Ray, S.S. Density Functional Theory Interaction Study of a Polyethylene Glycol-Based Nanocomposite with Cephalexin Drug for the Elimination of Wound Infection. ACS Omega 2022.
  5. Tandon, H.; Chakraborty, T.; Suhag, V. A brief review on importance of DFT in drug design. Res. Med. Eng. Stud. 2019, 39, 46.
  6. Ye, N.; Yang, Z.; Liu, Y. Applications of density functional theory in COVID-19 drug modeling. Drug Discov. Today 2022, 27, 1411–1419.
  7. Zhu, B.; Cheng, B.; Zhang, L.; Yu, J. Review on DFT calculation of s-triazine-based carbon nitride. Carbon Energy 2019, 1, 32–56.
  8. Kim, D.H.; Kim, D.W.; Jang, J.Y.; Lee, N.; Ko, Y.-J.; Lee, S.M.; Kim, H.J.; Na, K.; Son, S.U. Fe3O4@ organic polymer-based multifunctional drug delivery systems: Targeting, imaging, and magneto-thermal behaviors. ACS Appl. Mater. Interfaces 2020, 12, 37628–37636.
  9. Kazemi, S.; Daryani, A.S.; Abdouss, M.; Shariatinia, Z. DFT computations on the hydrogen bonding interactions between methacrylic acid-trimethylolpropane trimethacrylate copolymers and letrozole as drug delivery systems. J. Theor. Comput. Chem. 2016, 15, 1650015.
  10. Karataş, D.; Tekin, A.; Bahadori, F.; Çelik, M.S. Interaction of curcumin in a drug delivery system including a composite with poly(lactic-co-glycolic acid) and montmorillonite: A density functional theory and molecular dynamics study. J. Mater. Chem. B 2017, 5, 8070–8082.
  11. Farzad, F.; Hashemzadeh, H. Probing the effect of polyethene glycol on the adsorption mechanisms of Gem on the hexagonal boron nitride as a highly efficient polymer-based drug delivery system: DFT, classical MD and Well-tempered Metadynamics simulations. J. Mol. Graph. Model. 2020, 98, 107613.
  12. Raha, K.; Peters, M.B.; Wang, B.; Yu, N.; Wollacott, A.M.; Westerhoff, L.M.; Merz, K.M. The role of quantum mechanics in structure-based drug design. Drug Discov. Today 2007, 12, 725–731.
  13. Blatt, J.M. Practical points concerning the solution of the Schrödinger equation. J. Comput. Phys. 1967, 1, 382–396.
  14. Nisar, K.S.; Ali, K.K.; Inc, M.; Mehanna, M.S.; Rezazadeh, H.; Akinyemi, L. New solutions for the generalized resonant nonlinear Schrödinger equation. Results Phys. 2022, 33, 105153.
  15. Burke, K.; Wagner, L.O. DFT in a nutshell. Int. J. Quantum Chem. 2013, 113, 96–101.
  16. Parr, R.G. Density functional theory of atoms and molecules. In Horizons of Quantum Chemistry; Springer: Berlin/Heidelberg, Germany, 1980; pp. 5–15.
  17. Bagayoko, D. Understanding density functional theory (DFT) and completing it in practice. AIP Adv. 2014, 4, 127104.
  18. Makkar, P.; Ghosh, N.N. A review on the use of DFT for the prediction of the properties of nanomaterials. RSC Adv. 2021, 11, 27897–27924.
  19. Ma, Z.; Wu, J.; Sun, M.; Li, B.; Yu, X. Disulfur-bridged polyethyleneglycol/DOX nanoparticles for the encapsulation of photosensitive drugs: A case of computational simulations on the redox-responsive chemo-photodynamic drug delivery system. RSC Adv. 2021, 11, 37988–37994.
  20. Kim, K.; Lee, S.; Jin, E.; Palanikumar, L.; Lee, J.H.; Kim, J.C.; Nam, J.S.; Jana, B.; Kwon, T.-H.; Kwak, S.K.; et al. MOF × Biopolymer: Collaborative Combination of Metal–Organic Framework and Biopolymer for Advanced Anticancer Therapy. ACS Appl. Mater. Interfaces 2019, 11, 27512–27520.
  21. Shah, M.R.; Yadav, G.D. Prediction of sorption in polymers using quantum chemical calculations: Application to polymer membranes. J. Membr. Sci. 2013, 427, 108–117.
  22. Cortes, E.; Márquez, E.; Mora, J.R.; Puello, E.; Rangel, N.; De Moya, A.; Trilleras, J. Theoretical Study of the Adsorption Process of Antimalarial Drugs into Acrylamide-Base Hydrogel Model Using DFT Methods: The First Approach to the Rational Design of a Controlled Drug Delivery System. Processes 2019, 7, 396.
  23. Abdel-Bary, A.S.; Tolan, D.A.; Nassar, M.Y.; Taketsugu, T.; El-Nahas, A.M. Chitosan, magnetite, silicon dioxide, and graphene oxide nanocomposites: Synthesis, characterization, efficiency as cisplatin drug delivery, and DFT calculations. Int. J. Biol. Macromol. 2020, 154, 621–633.
  24. Mahdavian, L. DFT studies of the drug carrier of anti-migraine (sumatriptan) on nano-graphene oxide (NGO) and graphene oxide/polyethylene glycol polymer nano-composite. Diam. Relat. Mater. 2020, 104, 107745.
  25. Madadi Mahani, N. Quantum Chemical Study of Interaction of PLGA Polymeric Nanoparticles as Drug Delivery with Anti-Cancer Agents of Thiazoline. Int. J. New Chem. 2019, 6, 34–42.
  26. Li, X.; McTaggart, M.; Malardier-Jugroot, C. Synthesis and characterization of a pH responsive folic acid functionalized polymeric drug delivery system. Biophys. Chem. 2016, 214–215, 17–26.
  27. Li, Y. A Study of the Incorporation of Antischistosomiasis Drugs into Polyheterocycles and DFT Calculations on Polymer Precursors. Ph.D. Thesis, University of Portsmouth, Portsmouth, UK, 2010.
  28. Rajan, M.; Murugan, M.; Ponnamma, D.; Sadasivuni, K.K.; Munusamy, M.A. Poly-carboxylic acids functionalized chitosan nanocarriers for controlled and targeted anti-cancer drug delivery. Biomed. Pharmacother. 2016, 83, 201–211.
  29. Gong, P.; Zhang, L.; Yuan, X.-a.; Liu, X.; Diao, X.; Zhao, Q.; Tian, Z.; Sun, J.; Liu, Z.; You, J. Multifunctional fluorescent PEGylated fluorinated graphene for targeted drug delivery: An experiment and DFT study. Dyes Pigment. 2019, 162, 573–582.
  30. Shariatinia, Z.; Mazloom-Jalali, A. Chitosan nanocomposite drug delivery systems designed for the ifosfamide anticancer drug using molecular dynamics simulations. J. Mol. Liq. 2019, 273, 346–367.
  31. Bazyari-Delavar, S.; Badalkhani-Khamseh, F.; Ebrahim-Habibi, A.; Hadipour, N.L. Investigation of host-guest interactions between polyester dendrimers and ibuprofen using density functional theory (DFT). Comput. Theor. Chem. 2020, 1189, 112983.
  32. Bazyari-Delavar, S.; Badalkhani-Khamseh, F.; Ebrahim-Habibi, A.; Hadipour, N.L. PAMAM and polyester dendrimers as favipiravir nanocarriers: A comparative study using DFT method. J. Nanoparticle Res. 2021, 23, 231.
  33. Bai, L.; Yan, H.; Bai, T.; Feng, Y.; Zhao, Y.; Ji, Y.; Feng, W.; Lu, T.; Nie, Y. High fluorescent hyperbranched polysiloxane containing β-cyclodextrin for cell imaging and drug delivery. Biomacromolecules 2019, 20, 4230–4240.
  34. Deka, B.C.; Bhattacharyya, P.K. Understanding chitosan as a gene carrier: A DFT study. Comput. Theor. Chem. 2015, 1051, 35–41.
  35. Kumar, K.; Castaño, E.J.; Weidner, A.R.; Yildirim, A.; Goodwin, A.P. Depolymerizable Poly(O-vinyl carbamate-alt-sulfones) as Customizable Macromolecular Scaffolds for Mucosal Drug Delivery. ACS Macro Lett. 2016, 5, 636–640.
  36. Haghighi, F.; Morsali, A.; Bozorgmehr, M.R.; Beyramabadi, S.A. Nanostructures of PAMAM Dendrimers in Drug Delivery system for 5-fluorouracil. J. Sib. Fed. Univ. Chem. 2020, 13, 309–323.
  37. Morsali, A.; Harati, H.; Bozorgmehr, M.R.; Beyramabadi, S.A. DFT investigation of chitosan nanoparticle as hydroxyurea nanocarrier. J. Sib. Fed. Univ. Chem. 2022, 11, 46–57.
  38. Shamim, M.; Perveen, M.; Nazir, S.; Hussnain, M.; Mehmood, R.; Khan, M.I.; Iqbal, J. DFT study of therapeutic potential of graphitic carbon nitride (g-C3N4) as a new drug delivery system for carboplatin to treat cancer. J. Mol. Liq. 2021, 331, 115607.
  39. Shahabi, M.; Raissi, H. Investigation of the solvent effect, molecular structure, electronic properties and adsorption mechanism of Tegafur anticancer drug on Graphene nanosheet surface as drug delivery system by molecular dynamics simulation and density functional approach. J. Incl. Phenom. Macrocycl. Chem. 2017, 88, 159–169.
  40. Rose, P.W.; Prlić, A.; Altunkaya, A.; Bi, C.; Bradley, A.R.; Christie, C.H.; Costanzo, L.D.; Duarte, J.M.; Dutta, S.; Feng, Z. The RCSB protein data bank: Integrative view of protein, gene and 3D structural information. Nucleic Acids Res. 2017, 45, D271–D281.
  41. Li, Q.; Cheng, T.; Wang, Y.; Bryant, S.H. PubChem as a public resource for drug discovery. Drug Discov. Today 2010, 15, 1052–1057.
  42. Kim, S.; Thiessen, P.A.; Bolton, E.E.; Chen, J.; Fu, G.; Gindulyte, A.; Han, L.; He, J.; He, S.; Shoemaker, B.A. PubChem substance and compound databases. Nucleic Acids Res. 2016, 44, D1202–D1213.
  43. Karimzadeh, S.; Safaei, B.; Jen, T.-C. Theorical investigation of adsorption mechanism of doxorubicin anticancer drug on the pristine and functionalized single-walled carbon nanotube surface as a drug delivery vehicle: A DFT study. J. Mol. Liq. 2021, 322, 114890.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Others
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Oluwasegun Chijioke Adekoya
,
Gbolahan Joseph Adekoya
,
Emmanuel Rotimi Sadiku
,
Yskandar Hamam
,
Suprakas Sinha Ray
View Times: 812
Entry Collection: Biopharmaceuticals Technology
Revisions: 2 times (View History)
Update Date: 18 Oct 2022
Table of Contents
    1000/1000
    Hot Most Recent
    Video Production Service
    Feedback