Your browser does not fully support modern features. Please upgrade for a smoother experience.

Submitted Successfully!
Thank you for your contribution! You can also upload a video entry or images related to this topic.
For video creation, please contact our Academic Video Service.
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Srijib Das | -- | 1662 | 2022-08-30 08:54:16 | | | |
| 2 | Camila Xu | + 56 word(s) | 1718 | 2022-08-30 09:41:45 | | | | |
| 3 | Camila Xu | -1 word(s) | 1717 | 2022-09-01 08:10:54 | | | | |
| 4 | Camila Xu | + 17 word(s) | 1734 | 2022-09-02 05:29:40 | | |
Video Upload Options
We provide professional Academic Video Service to translate complex research into visually appealing presentations. Would you like to try it?
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Das, S.; Ghosh, S.; Kuila, T.; Murmu, N.C.; Kundu, A. Fundamentals of Oxygen Reduction Reaction. Encyclopedia. Available online: https://encyclopedia.pub/entry/26657 (accessed on 03 March 2026).
Das S, Ghosh S, Kuila T, Murmu NC, Kundu A. Fundamentals of Oxygen Reduction Reaction. Encyclopedia. Available at: https://encyclopedia.pub/entry/26657. Accessed March 03, 2026.
Das, Srijib, Souvik Ghosh, Tapas Kuila, Naresh Chandra Murmu, Aniruddha Kundu. "Fundamentals of Oxygen Reduction Reaction" Encyclopedia, https://encyclopedia.pub/entry/26657 (accessed March 03, 2026).
Das, S., Ghosh, S., Kuila, T., Murmu, N.C., & Kundu, A. (2022, August 30). Fundamentals of Oxygen Reduction Reaction. In Encyclopedia. https://encyclopedia.pub/entry/26657
Das, Srijib, et al. "Fundamentals of Oxygen Reduction Reaction." Encyclopedia. Web. 30 August, 2022.
Copy Citation
Oxygen reduction reaction (ORR) has been the subject of huge investigation since it is at the heart of various energy conversion and storage systems such as fuel cells, metal-air batteries, and so on. The mechanistic pathway is governed not only by the oxygen adsorption mode, but it also depends on the dissociation barrier of the catalyst surface.
biomass
pyrolysis
porous carbon
heteroatom doping
1. Introduction
The rapidly increasing concerns regarding exhaustion of fossil fuel and environmental deterioration have gathered global awareness for renewable energy production to develop sustainable society. Recently, various electrochemical technologies are being adopted to execute the reduction of climate change, and environmental pollution. For example, fuel cells (FC), metal-air batteries (MABs), water electrolyzers, etc., have been regarded as dependable as well as clean, eco-friendly, and affordable energy storage/conversion devices [1]. The performance and efficiency of many energy conversions and storage systems are mainly governed by oxygen reduction reaction (ORR) which was firstly reported by Jasinski in 1964 using co-phthalocyanine as a precursor [2]. However, the ORR process is kinetically sluggish requiring high overpotential and hence, robust electrocatalysts are often required to trigger the ORR process. Until now, Pt-based materials are considered as the benchmark electrocatalysts for ORR in terms of achieving high positive onset potential, half-wave potential, and high limiting current density. Nonetheless, high cost, scarcity, and poor durability are the main constraints from make them industrially viable.
Recently, the main aim of the researchers is to substitute Pt-based materials with cost-effective, efficient, and stable non-precious metal-based/metal-free materials. To achieve this goal, a library of platinum group metal (PGM) free electrocatalysts have been developed which can be divided into two branches: non-precious transition metal-based electrocatalysts including metal-coordinated nitrogen-doped carbon (M−N−C) [3][4][5], transition metal-based oxides [6], transition metal nitrides [7], phosphides [8], perovskites [9], transition metal chalcogenides [10], and heteroatom or multi atom doped carbon-based materials [11]. Although many electrocatalysts showed promising electrocatalytic activity toward ORR rivaling state-of-the-art Pt/C but there is plenty of room to improve the stability of these transition metal-based electrocatalysts to be considered for commercial uses.
Metal-free carbon-based materials have become a promising alternative to transition metals due to their organized electrical conductivity, durability, stability, tunable surface morphology, and adjustable (micro, meso, macro) porous structure. Moreover, the doping of heteroatom (N, P, S, B, etc.) in the sp2 carbon template can alter the electronic distribution over carbon owing to the generated electronegativity difference [3]. As a consequence, this will help to facilitate oxygen adsorption as well as the breaking of O-O bond rather than pristine carbon. It is important to mention that the advent of carbon nanotubes (CNTs) and graphene have profoundly encouraged the development of carbon-based electrodes for ORR. In spite of the promising performance of CNT or graphene-based materials in ORR, their utilization on a large scale is hindered by the high synthetic costs. Hence, highly earth-abundant biomass resources have garnered attention as sustainable and alternative option to design carbon-based materials for green energy storage devices due to their low cost, and inherent presence of heteroatoms.
The main resources of biomass are carbohydrates, polysaccharides, lignocellulose biomass, animal-based biomass, human waste-based biomass, etc. which are globally produced as waste in tons every single day [12]. These wastes pose a great challenge to waste management and this can be regarded as a potential option to convert the waste to novel carbon-based materials for versatile electrochemical applications. Indeed, the conversion of biomass to electrode materials for energy and environmental applications gained huge attention and has been highlighted recently [13][14][15]. Cellulose, hemicellulose, and lignin’s are the primary configurational components of biomass [12].
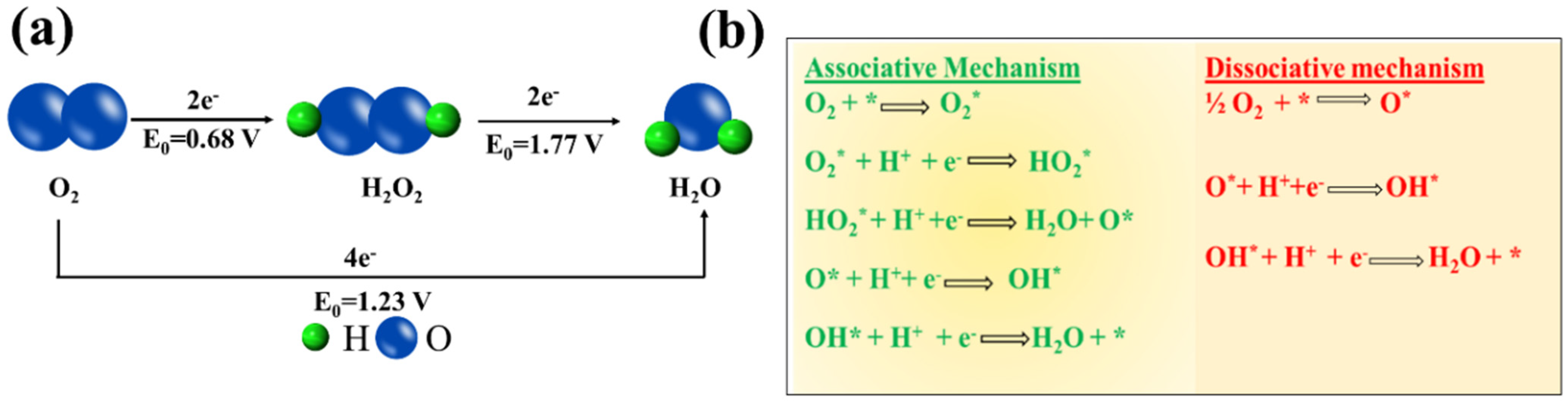
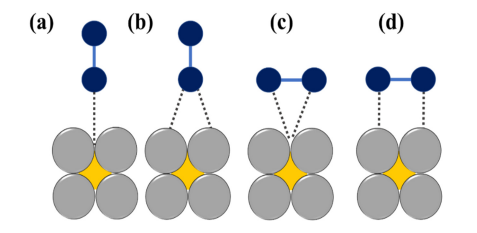 Figure 2. The schematic illustration of various modes of O2 adsorption on catalyst surfaces: (a) on top end-on; (b) bridge end-on; (c) bridge side-on one site; and d, bridge side-on two sites, adapted from [23].
Figure 2. The schematic illustration of various modes of O2 adsorption on catalyst surfaces: (a) on top end-on; (b) bridge end-on; (c) bridge side-on one site; and d, bridge side-on two sites, adapted from [23].
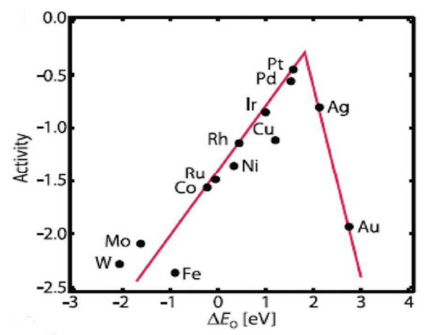 Figure 3. Trends in oxygen reduction activity plotted as a function of the oxygen-binding energy, adapted from [25].
Figure 3. Trends in oxygen reduction activity plotted as a function of the oxygen-binding energy, adapted from [25].
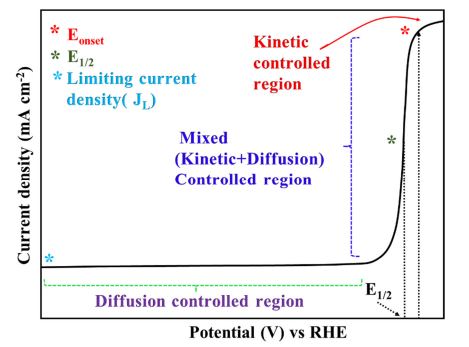 Figure 4. Typical LSV polarization curve for ORR with different regions.
where
Figure 4. Typical LSV polarization curve for ORR with different regions.
where
2. Fundamentals of ORR
ORR has been the subject of huge investigation over the decades (Figure 1a) since it is at the heart of various energy conversion and storage systems such as fuel cells, metal-air batteries, and so on [16][17]. Among all the studied catalysts, Pt is the state-of-the-art catalyst for ORR due to its moderate affinity to the reactive intermediate species formed on the surface of an electrode during the course of the reaction. Moreover, Pt possesses the highest electrochemical activity towards ORR owing to its appropriate d–band vacancy (0.6 per atom), and reasonable oxygen adsorption capability [18]. Until now, various mechanism for ORR has been put forward, however; it can follow either dissociative or associative one (Figure 1b).

Figure 1. (a) Scheme of the ORR mechanism by direct pathway and indirect pathway, (b) ORR mechanism on the catalyst surface (* notation denotes a site on the catalyst surface).
The mechanistic pathway is governed not only by the oxygen adsorption mode, but it also depends on the dissociation barrier of the catalyst surface [19]. The adsorption of O2 over the active site of the catalyst is mainly of two types: bidentate O2 adsorption (Yeager model) and end-on or monodentate O2 adsorption (Figure 2) [20]. The first one leads to the direct four-electron pathway resulting in H2O as the product whereas the second one follows a two-electron pathway with peroxide formation, respectively [21][22].
 Figure 2. The schematic illustration of various modes of O2 adsorption on catalyst surfaces: (a) on top end-on; (b) bridge end-on; (c) bridge side-on one site; and d, bridge side-on two sites, adapted from [23].
Figure 2. The schematic illustration of various modes of O2 adsorption on catalyst surfaces: (a) on top end-on; (b) bridge end-on; (c) bridge side-on one site; and d, bridge side-on two sites, adapted from [23].It is noteworthy to mention that for practical applications like fuel cells, metal-air batteries, etc., the four-electron pathway is a more desired one since the formation of peroxide species can be avoided which caters to the degradation of the catalyst. The formation of highly reactive oxygen intermediates in ORR such as OOH*, OH*, O* (* denotes a site on the catalyst surface) is associated with the involvement of a complicated multi-step electron transfer process. The electrocatalytic activity is largely determined by the binding energies of the reactive oxygen species to the catalyst surface. Hence, to design highly active materials it is a prerequisite to have knowledge of how to control the binding energies of reactive intermediates on a catalyst surface. On the basis of density functional theory calculations, Nørskov and his group have calculated the free energies of the surface intermediates for a series of metals [19]. This group has also established a trend in thermodynamic limitations for the metals and constructed a volcano-shaped plot that relates the theoretical ORR activity and oxygen adsorption energy. The model indicates that Pt sits near the top and explains why Pt is regarded as the best cathode material. However, it is important to note that Pt is not situated at the “summit of the volcano” (Figure 3) and hence alloying with 3d transition metals can be used to improve its performance [24].
 Figure 3. Trends in oxygen reduction activity plotted as a function of the oxygen-binding energy, adapted from [25].
Figure 3. Trends in oxygen reduction activity plotted as a function of the oxygen-binding energy, adapted from [25]. 2.1. Basic Parameters to Evaluate ORR Catalysts
After Levich’s seminal discovery of the rotating disk electrode (RDE) in 1944, it is widely used to study the ORR kinetics from the polarization curve [26]. The polarization curve is generally divided into three well-defined regions namely kinetic, mixed (kinetic + diffusion), and diffusion-limited zone and in each part, the ORR kinetics are controlled in different ways. Apart from that, some widely accepted parameters such as the onset potential (Eonset), half-wave potential (E1/2), and diffusion-limited current density (JL) can be deduced from the polarization curve for apprising the electrochemical activity of the investigated electrocatalyst. These parameters will be defined later but it is necessary to highlight that the more positive the Eonset, E1/2, and high JL values, the more active the electrocatalyst for ORR. In the kinetic-controlled area, the ORR reaction is sluggish, and the current density increases to some extent as the potential decreases (Figure 4). In a mixed (kinetic and diffusion-controlled zone) region, the reaction accelerates as the potential drops and a remarkable increase in the current density can be observed. In this particular region, the current density is inversely proportional to the applied potential. In the diffusion-controlled zone (plateau region of the curve), the current density can be precisely determined by convection, and it reaches a platform at a certain rotating speed.
 Figure 4. Typical LSV polarization curve for ORR with different regions.
Figure 4. Typical LSV polarization curve for ORR with different regions.2.1.1. Onset Potential and Half-Wave Potential
The definitions of the Eonset vary a lot in literature and the experimental determination is also quite arbitrary. However, onset potential usually refers to the potential when the current diverges from the baseline and the most common approach is to find the intersection of the tangents between the baseline and the increasing current in the polarization curve (Figure 4). Apart from that, the potential corresponding to 5% of the JL and the potential at which the ORR current density does not exceed a value of 0.1 mA cm−2 were also proposed to define the onset potential [27]. E1/2 is another basic parameter, and it is directly calculated from the midpoint of obtained LSV curve at 1600 rpm. It is basically the potential corresponding to half of the diffusion limiting current density.
2.1.2. Kinetic Current Density
Kinetic current density (Jk) is one of the important parameters to determine the catalytic activity of an ORR catalyst. Mass transport corrected polarization curve predicts the value of Jk and can be obtained with the help of Koutecky-Levich (K-L) equation:
1/J = 1/Jk + 1/JL
To minimize the error in mass transport correction, different catalysts are compared with respect to kinetic current density at a higher potential region.
2.1.3. Electron Transfer Number and HO2− Percentage
The number of electron transfer (n) and the percentage of HO2− intermediate are also basic parameters to understand ORR kinetics. These parameters can be determined from RDE or RRDE (rotating ring disk electrode) techniques which are effective for investigating the kinetics of multistep charge transfer reactions. K-L equation is generally utilized to calculate the “n” value and obtained by plotting (1/JL) against the square root of rotation rate (ω−1/2), which is widely known as the K-L plot.
For
RDE, JL = Bω1/2
B = 0.62 nFC0 (D0)2/3 ν−1/6
where, ω is the electrode rotating rate (rad s−1), n is the number of electrons, F is the Faraday constant (F = 96485 C mol−1), C0 (C0 = 1.2 × 10−6 mol cm−3) and D0 (D0 = 1.9 × 10−5 cm2 s−1) denotes the concentration and diffusion coefficients of O2 in 0.1 M KOH, respectively, υ is the kinematic viscosity of the electrolyte (0.01 cm2 s−1), and k is the electron transfer rate constant [28]. The “n” value can also be calculated from the RRDE technique by using the following equation:
4JD = n (JD + JR/N)
where JD is the disc current density, JR is the ring current density, and N is the RRDE collection efficiency, n is the number of electron transfers during the reaction. The percentage of intermediate species for ORR is calculated by the equation given below:
% HO2− = 200JR/(NJD + JR)
References
- Borghei, M.; Lehtonen, J.; Liu, L.; Rojas, O.J. Advanced biomass-derived electrocatalysts for the oxygen reduction reaction. Adv. Mater. 2018, 30, 1703691.
- Jasinski, R. A New Fuel cell cathode catalyst. Nature 1964, 201, 1212–1213.
- Yang, L.; Shui, J.; Du, L.; Shao, Y.; Liu, J.; Dai, L.; Hu, Z. Carbon-based metal-free ORR electrocatalysts for fuel cells: Past, present, and future. Adv. Mater. 2019, 31, 1804799.
- Chen, D.; Li, G.; Chen, X.; Zhang, Q.; Sui, J.; Li, C.; Zhang, Y.; Hu, J.; Yu, J.; Yu, L. Developing nitrogen and Co/Fe/Ni multi-doped carbon nanotubes as high-performance bifunctional catalyst for rechargeable zinc-air battery. J. Colloid Interface Sci. 2021, 593, 204–213.
- Seh, Z.W.; Kibsgaard, J.; Dickens, C.F.; Chorkendorff, I.B.; Nørskov, J.K.; Jaramillo, T.F. Combining theory and experiment in electrocatalysis: Insights into materials design. Science 2017, 355, eaad4998.
- Doan, T.L.L.; Tran, D.T.; Nguyen, D.C.; Kim, D.H.; Kim, N.H.; Lee, J.H. Rational engineering CoxOy nanosheets via phosphorous and sulfur dual-coupling for enhancing water splitting and Zn–air battery. Adv. Funct. Mater. 2021, 31, 2007822.
- Cui, Z.; Fu, G.; Li, Y.; Goodenough, J.B. Ni3FeN-Supported Fe3Pt intermetallic nano alloy as a high-performance bifunctional catalyst for metal-air batteries. Angew Chem. Int. Ed. 2017, 56, 9901–9905.
- Li, H.; Li, Q.; Wen, P.; Williams, T.B.; Adhikari, S.; Dun, C.; Lu, C.; Itanze, D.; Jiang, L.; Carroll, D.L. Colloidal cobalt phosphide nanocrystals as trifunctional electrocatalysts for overall water splitting powered by a zinc-air battery. Adv. Mater. 2018, 30, 1705796.
- Huang, S.-J.; Muneeb, A.; Sabhapathy, P.; Sheelam, A.; Bayikadi, K.S.; Sankar, R. Tailoring the Co 4+/Co 3+ active sites in a single perovskite as a bifunctional catalyst for the oxygen electrode reactions. Dalton Trans. 2021, 50, 7212–7222.
- Shi, X.; Ling, X.; Li, L.; Zhong, C.; Deng, Y.; Han, X.; Hu, W. Nanosheets assembled into nickel sulfide nanospheres with enriched Ni3+ active sites for efficient water-splitting and zinc–air batteries. J. Mater. Chem. A 2019, 7, 23787–23793.
- Wang, Y.; Li, J.; Wei, Z. Recent progress of carbon-based materials in oxygen reduction reaction catalysis. ChemElectroChem 2018, 5, 1764–1774.
- Dhyani, V.; Bhaskar, T. A Comprehensive review on the pyrolysis of lignocellulosic biomass. Renew. Energy 2018, 129, 695–716.
- Wang, J.; Nie, P.; Ding, B.; Dong, S.; Hao, X.; Dou, H.; Zhang, X. Biomass derived carbon for energy storage devices. J. Mater. Chem. A 2017, 5, 2411–2428.
- Saini, S.; Chand, P.; Joshi, A. Biomass derived carbon for supercapacitor applications. J. Energy Storage 2021, 39, 102646.
- Chakraborty, R.; Vilya, K.; Pradhan, M.; Nayak, A.K. Recent advancement of biomass-derived porous carbon based materials for energy and environmental remediation applications. J. Mater. Chem. A 2022, 10, 6965–7005.
- Machan, C.W. Advances in the molecular catalysis of dioxygen reduction. ACS Catal. 2020, 10, 2640–2655.
- Katsounaros, I.; Cherevko, S.; Zeradjanin, A.R.; Mayrhofer, K.J.J. Oxygen electrochemistry as a cornerstone for sustainable energy conversion. Angew. Chem. Int. Ed. 2014, 53, 102–121.
- Rao, M.L.; Damjanovic, A.; Bockris, J.O. Oxygen adsorption related to the unpaired d-electrons in transition metals. J. Phys. Chem. 1963, 67, 2508–2509.
- Nørskov, J.K.; Rossmeisl, J.; Logadottir, A.; Lindqvist, L.; Kitchin, J.R.; Bligaard, T.; Jonsson, H. Origin of the overpotential for oxygen reduction at a fuel-cell cathode. J. Phys. Chem. B 2004, 108, 17886–17892.
- Worku, A.K.; Ayele, D.W.; Habtu, N.G. Recent advances and future perspectives in engineering of bifunctional electrocatalysts for rechargeable zinc–air batteries. Mater. Today Adv. 2021, 9, 100116.
- Lee, B.; Seo, H.R.; Lee, H.R.; Yoon, C.S.; Kim, J.H.; Chung, K.Y.; Cho, B.W.; Oh, S.H. Critical role of pH evolution of electrolyte in the reaction mechanism for rechargeable zinc batteries. ChemSusChem 2016, 9, 2948–2956.
- Ginting, R.T.; Ovhal, M.M.; Kang, J.-W. A novel design of hybrid transparent electrodes for high performance and ultra-flexible bifunctional electrochromic-supercapacitors. Nano Energy 2018, 53, 650.
- Worku, A.K.; Ayele, D.W.; Habtu, N.G. Recent advances and future perspectives in engineering of bifunctional electrocatalysts for rechargeable zinc–air batteries. Mater. Today Adv. 2021, 9, 100116.
- Stamenkovic, V.R.; Fowler, B.; Mun, B.S.; Wang, G.; Ross, P.N.; Lucas, C.A.; Markovic, N.M. Improved oxygen reduction activity on Pt3Ni (111) via increased surface site availability. Science 2007, 315, 493–497.
- Seh, Z.W.; Kibsgaard, J.; Dickens, C.F.; Chorkendorff, I.B.; Nørskov, J.K.; Jaramillo, T.F. Combining theory and experiment in electrocatalysis: Insights into materials design. Science 2017, 355, eaad4998.
- Levich, B. The theory of concentration polarisation. Discuss. Faraday Soc. 1947, 1, 37–49.
- Zhou, X.; Qiao, J.; Yang, L.; Zhang, J. A review of graphene-based nanostructural materials for both catalyst supports and metal-free catalysts in PEM fuel cell oxygen reduction reactions. Adv. Energy Mater. 2014, 4, 1301523.
- Kundu, A.; Samanta, A.; Raj, C.R. Hierarchical hollow MOF-derived bamboo-like N-doped carbon nanotube-encapsulated Co0.25Ni0.75 alloy: An efficient bifunctional oxygen electrocatalyst for zinc–air battery. ACS Appl. Mater. Interfaces 2021, 13, 30486–30496.
More
Information
Subjects:
Chemistry, Applied
Contributors
MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register
:
View Times:
7.7K
Revisions:
4 times
(View History)
Update Date:
02 Sep 2022
Notice
You are not a member of the advisory board for this topic. If you want to update advisory board member profile, please contact office@encyclopedia.pub.
OK
Confirm
Only members of the Encyclopedia advisory board for this topic are allowed to note entries. Would you like to become an advisory board member of the Encyclopedia?
Yes
No
${ textCharacter }/${ maxCharacter }
Submit
Cancel
Back
Comments
${ item }
|
More
No more~
There is no comment~
${ textCharacter }/${ maxCharacter }
Submit
Cancel
${ selectedItem.replyTextCharacter }/${ selectedItem.replyMaxCharacter }
Submit
Cancel
Confirm
Are you sure to Delete?
Yes
No





