Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Vicente Garcia-Santos
 -- 3964 2022-07-29 19:45:13 |
2 format
Jason Zhu
 -9 word(s) 3955 2022-08-01 04:33:36 |

Video Upload Options

We provide professional Video Production Services to translate complex research into visually appealing presentations. Would you like to try it?
No, upload directly Yes

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
García-Santos, V.;  Sánchez, J.M.;  Cuxart, J. Remote Sensing Land Surface Temperature-Based ET Algorithms. Encyclopedia. Available online: https://encyclopedia.pub/entry/25680 (accessed on 15 November 2024).
García-Santos V,  Sánchez JM,  Cuxart J. Remote Sensing Land Surface Temperature-Based ET Algorithms. Encyclopedia. Available at: https://encyclopedia.pub/entry/25680. Accessed November 15, 2024.
García-Santos, Vicente, Juan Manuel Sánchez, Joan Cuxart. "Remote Sensing Land Surface Temperature-Based ET Algorithms" Encyclopedia, https://encyclopedia.pub/entry/25680 (accessed November 15, 2024).
García-Santos, V.,  Sánchez, J.M., & Cuxart, J. (2022, July 29). Remote Sensing Land Surface Temperature-Based ET Algorithms. In Encyclopedia. https://encyclopedia.pub/entry/25680
García-Santos, Vicente, et al. "Remote Sensing Land Surface Temperature-Based ET Algorithms." Encyclopedia. Web. 29 July, 2022.
Remote Sensing Land Surface Temperature-Based ET Algorithms
Edit
This entry is adapted from the peer-reviewed paper 10.3390/rs14143440
Evapotranspiration (ET) is a process that includes evaporation from the surface, such as open water bodies, soil and vegetation, and transpiration as the water released mostly by the plant leaves transported from the root system. ET is a key factor in the hydrological cycle, since it describes the mechanism and energy needed to transport the liquid water stored in the soil-watershed-canopy system to the atmosphere, converted into water vapour.  Remote sensing technology is a globally consistent and economically feasible means to estimate ET values at regional and meso-scales on the Earth’s surface, since the approach directly links surface radiances and the components of the surface energy balance. Over the past, combined use of satellite remote sensing data from optical and thermal infrared sensors has provided substantial progress in the estimation of ET. Based on the concept of surface energy balance and net radiation, most remote sensing models have estimated ET for application studies such as water consumption, water resources planning and management over watersheds or modeling ecological processes and analyzing biophysical characteristics of landscape.
ET remote sensing land surface temperature (LST) atmospheric surface layer

1. Introduction

Evapotranspiration (ET) is a process that includes evaporation from the surface, such as open water bodies, soil and vegetation, and transpiration as the water released mostly by the plant leaves transported from the root system. ET is a key factor in the hydrological cycle, since it describes the mechanism and energy needed to transport the liquid water stored in the soil-watershed-canopy system to the atmosphere, converted into water vapour.
In the broader context, irrigated agriculture still accounts for 70% of freshwater withdrawals [1]. This is a serious problem noticed by the Horizon Europe program. In this framework, ET plays an important role as a controlling factor of the water cycle and energy transport among the biosphere, atmosphere and hydrosphere. The importance of ET has been evidenced from the very beginning of the Remote Sensing discipline, in application fields such as hydrology, for instance for the scheduling of field-scale irrigations and tillage [2] or in meteorology and climatology, for prediction of natural hazards such as floods and droughts [3] or in agriculture, where for vegetated surfaces, ET can be used as an indicator of plant water stress [4].
In situ ET field retrievals from ground instrumentation, based on conventional techniques (e.g., Eddy covariance, Bowen ratio, lysimetry, etc.), offer the advantage of a direct determination of the value of ET for a measuring site [5]. However, these instruments are often costly, their data require an adequate treatment which is quite time-consuming, and instrumental problems may happen [6]. A commonly-used alternative for the estimation of ET is the Penman-Monteith equation, which uses monitored variables (e.g., air temperature or humidity), very convenient with basic meteorological stations, especially in the form suggested by Food and Agriculture Organization (FAO) [7][8]. Furthermore, for an area which is spatially heterogeneous, measurements made in a single location may not be representative of the full area [9]. For a given area in a humid climate, annual ET can be as large as half of the precipitation, whereas for arid and semi-arid areas ET is almost equivalent to the total annual rainfall [10].
In summary, even if accurate ET estimates can be obtained for the instrumented sites, these values are not useful at larger scales due to the usual heterogeneity of the landscape and the complexity of the hydrological processes [2]. Conventional ground measurement techniques do not appreciate spatial distribution at large-scales, especially in regions composed of well-contrasted areas where advection may be important.

2. Single-Source Energy Balance Models

2.1. Surface Energy Balance Index (SEBI) and Simplified-SEBI (S-SEBI) Models

Originally proposed by [11], the physically-based assumption is that ET varies with the Ts for a homogeneous surface. For a given surface albedo and boundary layer conditions, there exists a temperature gradient between the surface and the atmosphere (Ts−Ta) at some crop height, that ranges from a maximum value for which ET is assumed to be zero, to a minimum value for which the potential ET (ETp) is taken, as given by the Penman-Monteith equation [7].
There exists a correlation between Ts and the surface reflectance (albedo), where for low reflectance values Ts remains constant with the progressive increase of such reflectance. This phenomenon is attributed to presence of body water or well-watered surfaces, where all the available energy is used for the evaporation. From certain reflectance threshold Ts increases with the reflectance, inducing a decrease in the evaporation, in the so-called “evaporation controlled” range. From another higher reflectance threshold, Ts decreases with the increase of the reflectance, because the Rn decreases due to the high reflection of the energy received, a process known as “radiation controlled”.
Based on the previous assumptions, for a specific surface given Ts, [11] provided a value for ET by means of an interpolation expression:
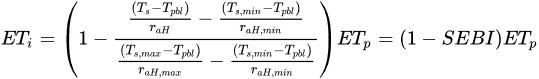
where Tpbl is the average air potential temperature at higher elevation or at the top of the Planetary Boundary Layer (pbl) and raH,min and raHmax are the minimum and maximum aerodynamic resistance in the sensible heat flux H [12].
A simplified version of the SEBI method (S-SEBI) was proposed by [13] with the advantage that no additional meteorological data are needed if the hydrological conditions of the surface are extreme enough to observe a significant range of gradient temperatures for the corresponding reflectance spectra.
Therefore if for a given αs value the two extremes of Ts exist, that is for Hmax (Ts,max, αs) and LEmax (Ts,min, αs), [13] expressed the ET value as:
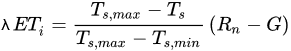
The method is called simplified if the wet and dry pixel conditions are observed for a specific albedo value in a satellite scene. But [13] simplified even more Equation (19) by adjusting linearly the trends of maximum and minimum Ts with the albedo, according the following equations:
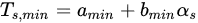
where amax and bmax are the slope and offset coefficients for the linear regression of the maximum temperature values with the albedo and amin and bmin are the corresponding coefficients for the linear regression of the minimum temperatures, also with the albedo. These four parameters must be adjusted in each individual satellite scene. Including Equations, ET expression from S-SEBI model can be defined then as:
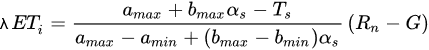
Very few modifications have been proposed in the literature for the S-SEBI model. One of them is made by [14], which in order to avoid using the LE and H fluxes, it is proposed using instead the evaporative fraction (EF), that can be extracted from the Ts-α scatterplot shape.
A recently study [15] proposed an adaptation of EVapotranspiration Assessment from SPAce (EVASPA) tool [16] to S-SEBI model. This model, denoted as E3S (for EVASPA S-SEBI Sahel), proposes two relevant changes. The first one is related to the handling of the algorithms determining the wet and dry edges, since in some regions like the Sahel with strong seasonal contrast only one edge may be identified. This led to the introduction of twelve additional seasonally-dependent algorithms to estimate the dry and wet points, using an ensemble member weighting. Secondly a cloud edge filtering method was implemented, to avoid that pixel outliers can distort the Ts scatterplot shape. The cloud edge filtering was developed in two levels: (1) the first level filter was based on the quality flag provided by the MODIS land surface temperature (LST) products. Thus, all pixels bordering clouds and associated with an LST error >1 K were removed; (2) a second level filter consisted in extending the first level filter to cloud-bordering pixels with LST below the first LST quartile in the entire image. This quantile level selection could be site and climate-specific.

2.2. Surface Energy Balance System (SEBS) Model

Proposed by [17] the SEBS method is based, as it is S-SEBI, SEBAL and METRIC (to be described below), on the same main concept as SEBI. The difference of SEBS from the rest is that it deals with estimating the ET fluxes at large scales, therefore considering heterogeneous surfaces.
Therefore, the assumption of constant atmospheric conditions for the whole scene is not applicable. Moreover, spatial variation of roughness height for different surfaces is allowed.
The SEBS is an extended model that defines the surface roughness length in the heat fluxes, reformulating the EF at the limiting cases. To this end in the SEBS theory the dry and wet case limits are:
Dry limit:
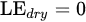
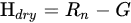
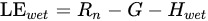
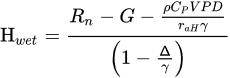
where VPD is the vapor pressure deficit (difference between saturated and non-saturated vapor pressure), Δ is the slope of the curve relating temperature difference (Ts-Ta) with VPD, and γ is the is the psychrometric constant.
As an intermediate step SEBS method defines a relative EF (EFr) as:
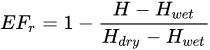
Some studies presented a modification of the SEBS inner structure in terms of: (i) momentum roughness length and zero plane displacement; (ii) an empirical relationship between land surface temperature and air temperature; and (iii) designing a new input interface of meteorological field at reference, with the objective of representing land surface and climatic changes of a specific region. These studies adapted SEBS to be applicable in different countries like Taiwan (SEBS-Taiwan, [18]), China (SEBS-China, [19]) or Iran (SEBS-Iran, [20]). SEBS was also modified at local scale (SEBS-Urban, [21]) after including the anthropogenic heat flux in the SEB equation to estimate the ET of Beijing city. This hypothesized that ET was equal to the water consumption in the study area.
An improvement of SEBS method was suggested by [22] by correcting the excess resistance with a scale factor dependent on soil moisture (SM), following:
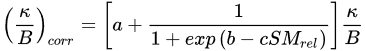
where a, b and c are coefficients of the sigmoid function and SMrel is a relative soil moisture defined as:
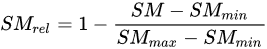
SMmax and SMmin values can be obtained using a time series analysis of the soil moisture data on annual or long-term basis [22]. Wu et al. [23] suggested the use of the Normal Differential Water Index (NDWI) instead of SMrel in Equations. Yi et al. [24] also recommended replacing SMrel by the inverse of the modified perpendicular drought index (MPDI).
It is also worth mentioning the study of Chen et al. [25], in which the excess resistance is internally modified to be robust for heat flux calculation for high and low canopies, since it has been proved its depends on environmental conditions, surface types, canopy structure and vegetation surface geometry. kB−1 structure was adjusted from a one-foliage layer to a multi-foliage layer, which provides the possibility of including the impact of vertical variations in foliage leaf area density, foliage shelter factor, and foliage heat transfer coefficient.

2.3. Surface Energy Balance Algorithm for Land (SEBAL) Model

Proposed by [26], SEBAL is an iterative and feedback-based numerical procedure that deduces the radiation, heat and evaporation fluxes. SEBAL estimates LE with the residual of Equations in a pixel by pixel satellite scene, just considering two anchor points (dry and wet points) for the full scene. At the dry point LE = 0 and H = Rn-G, and at the wet point H = 0 and LE can be considered either Rn-G or a reference ET [7].
The main consideration of SEBAL is to establish a linear regression between Ts and difference of Ts with the air temperature at the crop height z (δTa), as follows:
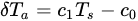
where c1 and c0 are the empirical coefficients derived from anchored conditions of wet (δTa,wet = 0, Ts,wet) and dry points (Ts,dry), for which the temperature difference is expressed as: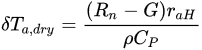
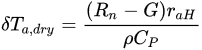
A first modification of SEBAL was proposed by [27] after introducing Digital elevation model (DEM) data to account for impacts of slope aspect on incident solar radiation. But the main subject of modification of SEBAL model is related with the choice of endmembers or anchor points (i.e., “hot” and “wet” points in the satellite scene). A Modified version of SEBAL (M-SEBAL) was proposed by [28], that based the election of the anchor (dry/wet) points on the type of surface, defined by the FVC. They adjusted Equations for every specific surface defined by FVC and subsequently estimated H and LE. Feng et al. [29] derived geo-mathematically four reference dry and wet limits, instead of the classical option of two anchor points.
Another modification is addressed in [30], where researchers deal with the endmember pixel selection process, proposing an automated procedure by introducing an exhaustive search algorithm (ESA), in which all possible candidates are systematically considered and checked to determine if the solution is satisfied, based on two steps: (1) create a binary map of candidate pixels that are identified using a simple rule-based classifier, and (2) apply ESA to identify hot and cold pixels that meet the defined criteria. In this sense, [31] created the automated SEBAL (ASEBAL) model that allows automatic selection of the endmember pixels according to criteria based on the variation in biophysical parameter values retrieved from satellite products.
It is also worth mentioning the study of [32], where researchers found more appropriate to combine the capabilities of Synthetic Aperture Radar (SAR) with optical remote sensing technique in the applications where soil moisture conditions to locate anchor pixels, since SAR is more suitable to detect soil moisture conditions.
Two interesting studies that suggested modifications of SEBAL ET model were related with changes in the SEB equation, by introducing new fluxes terms that must be accounted in certain situations. Mkhwanazi et al. [33] proposed a modified version of SEBAL model (SEBAL-A), that is capable of accounting for advection flux term, estimated with a wind function which included a daily mean or extreme temperatures parametrization, which is incorporated it into the original SEBAL daily ET sub-model. [34] also suggested enhancing the SEBAL model when it is applied in a heterogeneous urban environment (uSEBAL), after considering urban land surface parameters and including the urban anthropogenic heat flux in the SEB budget.
Finally, it is worth to note that recent open access software code versions of SEBAL are accessible. One of them is a new python version of SEBAL (pySEBAL), which incorporates an automated pixel selection procedure and is currently under development and testing at the IHE-Delft Institute [35]. In addition, a new tool based on the SEBAL algorithm, modified with a simplified version of the Calibration using Inverse Modeling at Extreme Conditions process [36] for the endmembers selection, was developed within the Google Earth Engine (geeSEBAL) environment [37].

2.4. Mapping Evapotranspiration at High Resolution and with Internalized Calibration (METRIC) Model

METRIC was proposed by [38], based almost completely on SEBAL method. The main differences with SEBAL are that Rn and Ts are corrected topographically using a Digital Elevation Model. Both methods differ in the calculation of H as in METRIC the temperature gradient of the wet point is expressed as: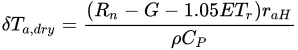
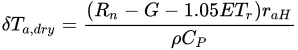
The assumption that ET rate (ETr) is about 5% above that of the standard ETr in the METRIC model is assumed because, for a large population of fields, some fields will have a wet soil surface beneath a full vegetation canopy that will tend to increase the total ET rate [38].
Since METRIC is directly based on SEBAL model, all the modifications previously discussed in Section 3.1.3 can also apply to METRIC. However, it is interesting to note a recent study [39], where calibration variability in METRIC is examined through the anchor pixels selection. Following METRIC original procedure to detect “cold” and “hot” pixel in a scene, the researchers detected a range of different “cold” and “hot” pixels that conformed a total of five sets of calibration pixel pairs (based on combination of maximum and minimum “cold” and “hot”, as well as values closest to the flux station). So, different slopes and intercept values were retrieved from the plot δT vs. Ts. In summary, researchers observed significant spatial differences in ET across the study area, which suggested that candidate calibration pixels cannot be completely quantified using only NDVI and Ts. Therefore, it can be presumed that the large differences in δT among the candidate pixels were not random noise, and that the inclusion of available energy into the calibration pixel selection process could potentially improve the calibration process and provide better estimates of ET.

3. Land Surface Temperatures–Vegetation Index Triangle/Trapezoidal ET Models

Vegetation Indices (VIs) offer important information from Ts−VI triangle/trapezoidal relationship. These diagrams can be useful for estimating regional ET values under the condition that full ranges of SM content and vegetation are present in the remote sensing scene.
The Triangle method was described by [40], and provides a biophysical justification for the combination of T and vegetation indices (VI) time series for land-cover mapping and land-cover change analysis. The lower envelope represents the wet edge, which is nearly constant and represents the lowest Ts for the different types of surfaces, assuming here that the ET is potential. Theoretically the two envelopes (dry and wet edges) intersect in a point of full cover vegetation and maximum ET.
Based on the Priestley-Taylor formulation [41] and fully remotely sensed data, an expression proposed by [42] allows estimating the LE according to the Ts−VI triangular relationship as:
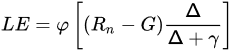
where φ varies from 0 to 1.26, and it is estimated with a two-step linear interpolation. This interpolation consists in: (1) once set a φmin = 0 (driest bare soil) and φmax = 1.26 (largest VI and lowest Ts), for each intermediate VI a φmin,i is estimated by interpolation between φmin and φmax and a φmax,i is assigned to the minimum Ts value of such VI (usually 1.26), (2) Different φi can be estimated from the Ts range at each VI. VI can be either the NDVI, FVC, the Soil Adjusted Vegetation Index (SAVI), Enhanced Vegetation Index (EVI), etc.
The Ts−VI Trapezoidal method based on the proposed Water Deficit Index (WDI) by [43], an index related to the ratio of actual and potential evapotranspiration, which evaluates the evapotranspiration rates of both full-cover and partially vegetated sites. WDI based Ts−VI Trapezoidal method considers that full covered vegetation can both water-stressed and well-watered in a satellite scene, so there is no intersect in a point of full cover vegetation and the Ts−VI diagram become a trapezoid. Moran et al. [43], extended the ET estimation from full to partially vegetated surface areas, considering that temperature gradient (Ts−Ta) varies linearly with the vegetation status. So, WDI is linearly related at each VI to the maximum (dry bare soil) and minimum (probably well-watered full-cover vegetation) gradient temperature, taking values between 0 and 1 and LE is calculated similar to Equation as the ratio of potential ET calculated from Penman-Monteith equation [7], LE for the trapezoidal method is expressed as:
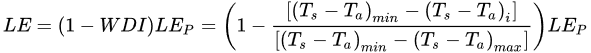
Stinsen et al. [44], combined the triangle method with thermal inertia information obtained from MSG-SEVIRI sensor, by changing the surface temperature over time. Researchers also applied a slightly modified version of the two-step interpolation scheme to obtain φ, based on a interpolation where the decomposition is regarded as non-linear with the argument that non-linear intersections are observed in the dry edge and in the iso-lines of equal moisture availability of the Ts−VI tringle feature. Adopting equations, [45] proposed a Time-Domain Triangle Method (TDTM), based on a pixel by pixel Ts–VI feature space, obtained by exploring the temporal domains over each single image pixel, since the triangle contains the whole climatic variability of the Ts–VI. Also, in [46], an algorithm to determine quantitatively the dry and wet edges for the Ts–VI triangular space in arid and semi-arid areas, where wet pixels are not generally easily identified, was developed with an iterative process that automatically retrieve the two edges in the Ts–FVC triangle space in ten steps. The process starts dividing the range of FVC in the Ts–FVC triangle space into M intervals evenly and ends with a linear regression to obtain the dry edge.
Another interesting modification of the Ts−VI triangle method is proposed by [47] that estimate daily ET directly using the top of atmosphere (TOA) radiances without performing atmospheric correction or other processes, to avoid the uncertainty associated with the estimation of ET, attributed to satellite data products. Furthermore, a recent study [48] estimates the soil heat flux (G) in the trapezoidal space of Ts-FVC, prior to apply the original Ts−VI trapezoidal method afterwards.

4. Dual (Two)-Source Energy Balance (TSEB) Model

A two-layer model of turbulent exchange that includes the view geometry associated with directional radiometric surface temperature was developed and evaluated by [49]. The main assumption of TSEB model is that Ts estimated from remote sensing measurements is the composite of soil and canopy surfaces, and it can be expressed as:
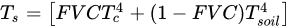
where Tc is the temperature of the canopy and Tsoil is the temperature of the non-vegetated soil. Note the term FVC in this Equation is a function of LAI and sensor viewing angle [50]. The original TSEB does not consider the weighting by the emissivities of each component, but some researchers have claimed for its importance [51][52][53].
The key of the TSEB model is the partition of sensible heat flux into the canopy and soil layers. If there is an interaction between the fluxes of both components, due to a heating of the in-canopy air by heat transport from the soil, the resistance framework in TSEB can be considered to be in series [49][54][55][56]. A parallel configuration was also introduced [49], based on the assumption that the resistance of each source interacts independently with respect to the surface-atmosphere, although the canopy still has an effect on the radiation transmitted towards the soil and the wind attenuation through the canopy to the soil surface. Each component has its own SEB equation expressed as: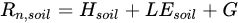
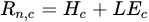
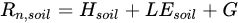
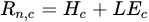
A variety of radiative transfer models have been implemented within TSEB to estimate Rn components. Traditional versions of TSEB estimate Rn using the physically-based radiative transfer model described in [57], first implemented within TSEB by [58]:
In this revised two-source model, the separation of net radiation between canopy and soil can be expressed as:
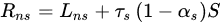
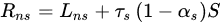
where S is solar radiation, τs is solar transmittance in the canopy, αs is soil albedo, αc is canopy albedo, LnS and LnC are longwave radiation for soil and canopy, respectively, and are estimated via the following expression:
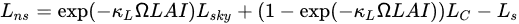
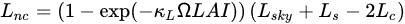
where LSky, LS, and LC are longwave radiation from the sky, soil, and canopy, and can be calculated from air, soil, and canopy temperature, Ω is the clumping factor, and κL is an extinction coefficient. Campbell and Norman [57] described how to estimate the transmittance, albedo, and extinction coefficients for soil and canopy.
Soil and canopy sensible heat fluxes H of Equations, can be deduced easily as:
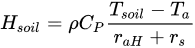
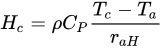
where the parameter rs is the resistance to the heat flow in the boundary layer immediately above the soil surface, and it can be expressed as:
where us is the wind speed at a height above the soil surface where the effect of soil surface roughness is minimal (i.e., 0.05–0.1 m).
Latent heat fluxes for soil (LEs) and canopy (LEc) are calculated as residuals of Equations.
Another type of two-source model formulation is the so-called patch model where it is assumed that all the fluxes act vertically and that there is no interaction between soil and canopy components (i.e., a complete energy balance between the atmosphere and each element [58][59]).
There exist modifications on the TSEB model, like the Two-Source Time-Integrated Model (TSTIM) proposed by [60], lately called Atmosphere-Land Exchange Inverse (ALEXI) in [61], which relates time-differential Ts observed (1.5–5.5 h after sunrise) from geostationary satellites to the time-integrated energy balance within the surface-atmospheric boundary layer system.
ALEXI has minimal reliance on absolute (instantaneous) air or surface temperature input data, and therefore provides a relatively robust flux determination at the coarse geostationary pixel scale (5–10 km). For finer scale ET applications, ALEXI flux fields can be spatially disaggregated using higher resolution Ts information from polar orbiting systems (e.g., Landsat or MODIS) in an algorithm referred to Disaggregated ALEXI (DisALEXI) model [62].
Another modified TSEB model is the Simplified TSEB (STSEB) model proposed by [63], which suggests dividing the Rn, H and LE fluxes in soil and canopy weighted values, according to the FVC. The scheme proposed by [64], which is based on canopy conductance by means of a formulation that has sound parameterizations of transpiration and evaporation, that links soil surface temperature and soil evaporation eliminating the need of using soil moisture as input, and allowing the model predicting surface temperature and energy fluxes simultaneously. Furthermore, it can be calibrated using remotely sensed LST data.

References

  1. FAO. The State of the World’s Land and Water Resources for Food and Agriculture–Systems at Breaking Point (SOLAW 2021); Synthesis Report; FAO: Rome, Italy, 2021.
  2. Idso, S.B.; Jackson, R.D.; Reginato, R.J. Estimating Evaporation: A Technique Adaptable to Remote Sensing. Science 1975, 189, 991–992.
  3. Brutsaert, W. Catchment-Scale Evaporation and the Atmospheric Boundary Layer. Water Resour. Res. 1986, 22, 39S–45S.
  4. Jackson, R.D.; Idso, S.B.; Reginato, R.J.; Pinter, P.J. Canopy Temperature as a Crop Water Stress Indicator. Water Resour. Res. 1981, 17, 1133–1138.
  5. Cuxart, J.; Boone, A.A. Evapotranspiration over Land from a Boundary-Layer Meteorology Perspective. Bound. Layer Meteorol. 2020, 177, 427–459.
  6. Allen, R.G.; Pereira, L.S.; Howell, T.A.; Jensen, M.E. Evapotranspiration Information Reporting: I. Factors Governing Measurement Accuracy. Agric. Water Manag. 2011, 98, 899–920.
  7. Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements—FAO Irrigation and Drainage Paper 56; FAO—Food and Agriculture Organization of the United Nations: Rome, Italy, 1998; ISBN 92-5-104219-5.
  8. Pereira, L.S.; Paredes, P.; Hunsaker, D.J.; López-Urrea, R.; Jovanovic, N. Updates and Advances to the FAO56 Crop Water Requirements Method. Agric. Water Manag. 2021, 248, 106697.
  9. Zhang, L.; Lemeur, R. Evaluation of Daily Evapotranspiration Estimates from Instantaneous Measurements. Agric. For. Meteorol. 1995, 74, 139–154.
  10. Engman, E.T.; Gurney, R.J. Remote Sensing in Hydrology; Chapman and Hall Ltd.: London, UK, 1991; ISBN 0412244500.
  11. Menenti, M.; Choudhury, B.J. Exchange Processes at the Land Surface for a Range of Space and Time Scales. In Proceedings of the Exchange Processes at the Land Surface for a Range of Space and Time Scales, Yokohama, Japan, 13–16 July 1993; IAHS Press: Wallingford, UK, 1993; pp. 561–568.
  12. Monin, A.S.; Obukhov, A.M. Basic Laws of Turbulent Mixing in the Surface Layer of the Atmosphere. Orig. Publ. Tr. Akad. Nauk SSSR Geophiz. Inst 1954, 24, 163–187.
  13. Roerink, G.J.; Su, Z.; Menenti, M. S-SEBI: A Simple Remote Sensing Algorithm to Estimate the Surface Energy Balance. Phys. Chem. Earth Part B 2000, 25, 147–157.
  14. Zhao, D.; Zhang, W.; Liu, C. A Modified S-SEBI Algorithm to Estimate Evapotranspiration Using Landsat ETM+ Image and Meteorological Data over the Hanjiang Basin, China. In Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–28 July 2007; pp. 3253–3256.
  15. Allies, A.; Demarty, J.; Olioso, A.; Moussa, I.B.; Issoufou, H.B.A.; Velluet, C.; Bahir, M.; Maïnassara, I.; Oï, M.; Chazarin, J.P.; et al. Evapotranspiration Estimation in the Sahel Using a New Ensemble-Contextual Method. Remote Sens. 2020, 12, 380.
  16. Gallego-Elvira, B.; Olioso, A.; Mira, M.; Reyes-Castillo, S.; Boulet, G.; Marloie, O.; Garrigues, S.; Courault, D.; Weiss, M.; Chauvelon, P.; et al. EVASPA (EVapotranspiration Assessment from SPAce) Tool: An Overview. Procedia Environ. Sci. 2013, 19, 303–310.
  17. Su, Z. The Surface Energy Balance System (SEBS) for Estimation of Turbulent Heat Fluxes. Hydrol. Earth Syst. Sci. 2002, 6, 85–99.
  18. Zhan, C.S.; Zhao, J.; Wang, H.X.; Yin, J. Quantitative Estimation of Land Surface Evapotranspiration in Taiwan Based on MODIS Data. Water Sci. Eng. 2011, 4, 237–245.
  19. Zhan, C.; Yin, J.; Wang, F.; Dong, Q. Regional Estimation and Validation of Remotely Sensed Evapotranspiration in China. Catena 2015, 133, 35–42.
  20. Jahangir, M.H.; Arast, M. Remote Sensing Products for Predicting Actual Evapotranspiration and Water Stress Footprints under Different Land Cover. J. Clean. Prod. 2020, 266, 121818.
  21. Cong, Z.T.; Shen, Q.N.; Zhou, L.; Sun, T.; Liu, J.H. Evapotranspiration Estimation Considering Anthropogenic Heat Based on Remote Sensing in Urban Area. Sci. China Earth Sci. 2017, 60, 659–671.
  22. Gokmen, M.; Vekerdy, Z.; Verhoef, A.; Verhoef, W.; Batelaan, O.; van der Tol, C. Integration of Soil Moisture in SEBS for Improving Evapotranspiration Estimation under Water Stress Conditions. Remote Sens. Environ. 2012, 121, 261–274.
  23. Wu, X.; Zhou, J.; Wang, H.; Li, Y.; Zhong, B. Evaluation of Irrigation Water Use Efficiency Using Remote Sensing in the Middle Reach of the Heihe River, in the Semi-Arid Northwestern China. Hydrol. Processes 2015, 29, 2243–2257.
  24. Yi, Z.; Zhao, H.; Jiang, Y.; Yan, H.; Cao, Y.; Huang, Y.; Hao, Z. Daily Evapotranspiration Estimation at the Field Scale: Using the Modified SEBS Model and HJ-1 Data in a Desert-Oasis Area, Northwestern China. Water 2018, 10, 640.
  25. Chen, X.; Massman, W.J.; Su, Z. A Column Canopy-Air Turbulent Diffusion Method for Different Canopy Structures. J. Geophys. Res. Atmos. 2019, 124, 488–506.
  26. Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holtslag, A.A.M. A Remote Sensing Surface Energy Balance Algorithm for Land (SEBAL). 1. Formulation. J. Hydrol. 1998, 212, 198–212.
  27. Allen, R.G.; Morse, A.; Tasumi, M.; Bastiaanssen, W.; Kramber, W.; Anderson, H. Evapotranspiration from Landsat (SEBAL) for Water Rights Management and Compliance with Multi-State Water Compacts. In Proceedings of the IGARSS 2001, Scanning the Present and Resolving the Future, IEEE 2001 International Geoscience and Remote Sensing Symposium, Sydney, Australia, 9–13 July 2001; IEEE: New York, NY, USA, 2002; Volume 2, pp. 830–833.
  28. Long, D.; Singh, V.P. A Modified Surface Energy Balance Algorithm for Land (M-SEBAL) Based on a Trapezoidal Framework. Water Resour. Res. 2012, 48.
  29. Feng, J.; Wang, Z. A Satellite-Based Energy Balance Algorithm with Reference Dry and Wet Limits. Int. J. Remote Sens. 2013, 34, 2925–2946.
  30. Bhattarai, N.; Quackenbush, L.J.; Im, J.; Shaw, S.B. A New Optimized Algorithm for Automating Endmember Pixel Selection in the SEBAL and METRIC Models. Remote Sens. Environ. 2017, 196, 178–192.
  31. Silva, A.M.; da Silva, R.M.; Santos, C.A.G. Automated Surface Energy Balance Algorithm for Land (ASEBAL) Based on Automating Endmember Pixel Selection for Evapotranspiration Calculation in MODIS Orbital Images. Int. J. Appl. Earth Obs. Geoinf. 2019, 79, 1–11.
  32. Prakash Mohan, M.M.; Rajitha, K.; Varma, M.R.R. A Novel Approach to Select Anchor Pixels in SEBAL Model by Using Inputs from SAR Images. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 7383–7386.
  33. Mkhwanazi, M.; Chávez, J.L.; Andales, A.A. SEBAL-A: A Remote Sensing ET Algorithm That Accounts for Advection with Limited Data. Part I: Development and Validation. Remote Sens. 2015, 7, 15046–15067.
  34. Faridatul, M.I.; Wu, B.; Zhu, X.; Wang, S. Improving Remote Sensing Based Evapotranspiration Modelling in a Heterogeneous Urban Environment. J. Hydrol. 2020, 581, 124405.
  35. Hessel, T.; van Opstal, J.; Trambauer, P.; Mohamed, Y.; Bastiaanssen, W. User Guide: PySEBAL for Landsat Imagery (Beta Version); IHE Delft Institute for Water Education: Delft, The Netherlands, 2017.
  36. Allen, R.G.; Burnett, B.; Kramber, W.; Huntington, J.; Kjaersgaard, J.; Kilic, A.; Kelly, C.; Trezza, R. Automated Calibration of the METRIC-Landsat Evapotranspiration Process. JAWRA J. Am. Water Resour. Assoc. 2013, 49, 563–576.
  37. Laipelt, L.; Kayser, R.H.B.; Santos Fleischmann, A.; Ruhoff, A.; Bastiaanssen, W.; Erickson, T.A.; Melton, F. Long-Term Monitoring of Evapotranspiration Using the SEBAL Algorithm and Google Earth Engine Cloud Computing. ISPRS J. Photogramm. Remote Sens. 2021, 178, 81–96.
  38. Allen, R.G.; Tasumi, M.; Trezza, R. Satellite-Based Energy Balance for Mapping Evapotranspiration with Internalized Calibration (METRIC)-Model. J. Irrig. Drain. Eng. 2007, 133, 380–394.
  39. Dhungel, S.; Barber, M.E. Estimating Calibration Variability in Evapotranspiration Derived from a Satellite-Based Energy Balance Model. Remote Sens. 2018, 10, 1695.
  40. LAMBIN, E.F.; Ehrlich, D. The Surface Temperature-Vegetation Index Space for Land Cover and Land-Cover Change Analysis. Int. J. Remote Sens. 1996, 17, 463–487.
  41. Priestley, C.H.B.; Taylor, R.J. On the Assessment of Surface Heat Flux and Evaporation Using Large-Scale Parameters. Mon. Weather Rev. 1972, 100, 81–92.
  42. Jiang, L.; Islam, S. A Methodology for Estimation of Surface Evapotranspiration over Large Areas Using Remote Sensing Observations. Geophys. Res. Lett. 1999, 26, 2773–2776.
  43. Moran, M.S.; Clarke, T.R.; Inoue, Y.; Vidal, A. Estimating Crop Water Deficit Using the Relation between Surface-Air Temperature and Spectral Vegetation Index. Remote Sens. Environ. 1994, 49, 246–263.
  44. Stisen, S.; Sandholt, I.; Nørgaard, A.; Fensholt, R.; Jensen, K.H. Combining the Triangle Method with Thermal Inertia to Estimate Regional Evapotranspiration—Applied to MSG-SEVIRI Data in the Senegal River Basin. Remote Sens. Environ. 2008, 112, 1242–1255.
  45. Minacapilli, M.; Consoli, S.; Vanella, D.; Ciraolo, G.; Motisi, A. A Time Domain Triangle Method Approach to Estimate Actual Evapotranspiration: Application in a Mediterranean Region Using MODIS and MSG-SEVIRI Products. Remote Sens. Environ. 2016, 174, 10–23.
  46. Tang, R.; Li, Z.L.; Tang, B. An Application of the Ts-VI Triangle Method with Enhanced Edges Determination for Evapotranspiration Estimation from MODIS Data in Arid and Semi-Arid Regions: Implementation and Validation. Remote Sens. Environ. 2010, 114, 540–551.
  47. Peng, J.; Liu, Y.; Zhao, X.; Loew, A. Estimation of Evapotranspiration from MODIS TOA Radiances in the Poyang Lake Basin, China. Hydrol. Earth Syst. Sci. 2013, 17, 1431–1444.
  48. Shekar, S.N.C.; Nandagiri, L. A Penman-Monteith Evapotranspiration Model with Bulk Surface Conductance Derived from Remotely Sensed Spatial Contextual Information. Int. J. Remote Sens. 2019, 41, 1486–1511.
  49. Norman, J.M.; Kustas, W.P.; Humes, K.S. Source Approach for Estimating Soil and Vegetation Energy Fluxes in Observations of Directional Radiometric Surface Temperature. Agric. For. Meteorol. 1995, 77, 263–293.
  50. Gómez, M.; Olioso, A.; Sobrino, J.A.; Jacob, F. Retrieval of Evapotranspiration over the Alpilles/ReSeDA Experimental Site Using Airborne POLDER Sensor and a Thermal Camera. Remote Sens. Environ. 2005, 96, 399–408.
  51. French, A.N.; Jacob, F.; Anderson, M.C.; Kustas, W.P.; Timmermans, W.; Gieske, A.; Su, Z.; Su, H.; McCabe, M.F.; Li, F.; et al. Surface Energy Fluxes with the Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) at the Iowa 2002 SMACEX Site (USA). Remote Sens. Environ. 2005, 99, 55–65.
  52. Sánchez, J.M.; Caselles, V.; Niclòs, R.; Coll, C.; Kustas, W.P. Estimating Energy Balance Fluxes above a Boreal Forest from Radiometric Temperature Observations. Agric. For. Meteorol. 2009, 149, 1037–1049.
  53. Häusler, M.; Conceição, N.; Tezza, L.; Sánchez, J.M.; Campagnolo, M.L.; Häusler, A.J.; Silva, J.M.N.; Warneke, T.; Heygster, G.; Ferreira, M.I. Estimation and Partitioning of Actual Daily Evapotranspiration at an Intensive Olive Grove Using the STSEB Model Based on Remote Sensing. Agric. Water Manag. 2018, 201, 188–198.
  54. Kustas, W.P.; Norman, J.M. Evaluation of Soil and Vegetation Heat Flux Predictions Using a Simple Two-Source Model with Radiometric Temperatures for Partial Canopy Cover. Agric. For. Meteorol. 1999, 94, 13–29.
  55. Anderson, M.C.; Norman, J.M.; Kustas, W.P.; Houborg, R.; Starks, P.J.; Agam, N. A Thermal-Based Remote Sensing Technique for Routine Mapping of Land-Surface Carbon, Water and Energy Fluxes from Field to Regional Scales. Remote Sens. Environ. 2008, 112, 4227–4241.
  56. Nieto, H.; Kustas, W.P.; Torres-Rúa, A.; Alfieri, J.G.; Gao, F.; Anderson, M.C.; White, W.A.; Song, L.; Alsina, M.d.M.; Prueger, J.H.; et al. Evaluation of TSEB Turbulent Fluxes Using Different Methods for the Retrieval of Soil and Canopy Component Temperatures from UAV Thermal and Multispectral Imagery. Irrig. Sci. 2019, 37, 389–406.
  57. Kustas, P.W.; Norman, J.M. Reply to Comments about the Basic Equations of Dual-Source Vegetation–Atmosphere Transfer Models. Agric. For. Meteorol. 1999, 94, 275–278.
  58. Blyth, E.M.; Harding, R.J. Application of Aggregation Models to Surface Heat Flux from the Sahelian Tiger Bush. Agric. For. Meteorol. 1995, 72, 213–235.
  59. Lhomme, J.P.; Chehbouni, A. Comments on Dual-Source Vegetation–Atmosphere Transfer Models. Agric. For. Meteorol. 1999, 94, 269–273.
  60. Anderson, M.C.; Norman, J.M.; Diak, G.R.; Kustas, W.P.; Mecikalski, J.R. A Two-Source Time-Integrated Model for Estimating Surface Fluxes Using Thermal Infrared Remote Sensing. Remote Sens. Environ. 1997, 60, 195–216.
  61. Mecikalski, J.R.; Diak, G.R.; Anderson, M.C.; Norman, J.M. Estimating Fluxes on Continental Scales Using Remotely Sensed Data in an Atmospheric-Land Exchange Model. J. Appl. Meteorol. 1999, 38, 1352–1369.
  62. Norman, J.M.; Anderson, M.C.; Kustas, W.P.; French, A.N.; Mecikalski, J.; Torn, R.; Diak, G.R.; Schmugge, T.J.; Tanner, B.C.W. Remote Sensing of Surface Energy Fluxes at 101-m Pixel Resolutions. Water Resour. Res. 2003, 39.
  63. Sánchez, J.M.; Kustas, W.P.; Caselles, V.; Anderson, M.C. Modelling Surface Energy Fluxes over Maize Using a Two-Source Patch Model and Radiometric Soil and Canopy Temperature Observations. Remote Sens. Environ. 2008, 112, 1130–1143.
  64. Gan, G.; Kang, T.; Yang, S.; Bu, J.; Feng, Z.; Gao, Y. An Optimized Two Source Energy Balance Model Based on Complementary Concept and Canopy Conductance. Remote Sens. Environ. 2019, 223, 243–256.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Remote Sensing
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Vicente García-Santos
,
Juan Manuel Sánchez
,
Joan Cuxart
View Times: 886
Revisions: 2 times (View History)
Update Date: 02 Aug 2022
Table of Contents
    1000/1000
    Hot Most Recent
    ScholarVision Creations
    Feedback