Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Foysal Ahammad
 -- 3501 2022-07-05 05:29:15 |
2 format correct
Vivi Li
 Meta information modification 3501 2022-07-05 08:55:54 | |
3 N/A
Md Afsar Ahmed Sumon
Meta information modification 3501 2022-08-01 15:04:46 |

Video Upload Options

Do you have a full video?
Send video materials Upload full video

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Hasan, M.R.;  Alsaiari, A.A.;  Fakhurji, B.Z.;  Molla, M.H.R.;  Asseri, A.H.;  Sumon, M.A.A.;  Park, M.N.;  Ahammad, F.;  Kim, B. Mathematical Modeling and Computational Tools in Drug Design. Encyclopedia. Available online: https://encyclopedia.pub/entry/24806 (accessed on 28 April 2024).
Hasan MR,  Alsaiari AA,  Fakhurji BZ,  Molla MHR,  Asseri AH,  Sumon MAA, et al. Mathematical Modeling and Computational Tools in Drug Design. Encyclopedia. Available at: https://encyclopedia.pub/entry/24806. Accessed April 28, 2024.
Hasan, Md Rifat, Ahad Amer Alsaiari, Burhan Zain Fakhurji, Mohammad Habibur Rahman Molla, Amer H. Asseri, Md Afsar Ahmed Sumon, Moon Nyeo Park, Foysal Ahammad, Bonglee Kim. "Mathematical Modeling and Computational Tools in Drug Design" Encyclopedia, https://encyclopedia.pub/entry/24806 (accessed April 28, 2024).
Hasan, M.R.,  Alsaiari, A.A.,  Fakhurji, B.Z.,  Molla, M.H.R.,  Asseri, A.H.,  Sumon, M.A.A.,  Park, M.N.,  Ahammad, F., & Kim, B. (2022, July 05). Mathematical Modeling and Computational Tools in Drug Design. In Encyclopedia. https://encyclopedia.pub/entry/24806
Hasan, Md Rifat, et al. "Mathematical Modeling and Computational Tools in Drug Design." Encyclopedia. Web. 05 July, 2022.
Mathematical Modeling and Computational Tools in Drug Design
Edit
This entry is adapted from the peer-reviewed paper 10.3390/molecules27134169

The conventional drug discovery approach is an expensive and time-consuming process, but its limitations have been overcome with the help of mathematical modeling and computational drug design approaches. Previously, finding a small molecular candidate as a drug against a disease was very costly and required a long time to screen a compound against a specific target. The development of novel targets and small molecular candidates against different diseases including emerging and reemerging diseases remains a major concern and necessitates the development of novel therapeutic targets as well as drug candidates as early as possible. In this regard, computational and mathematical modeling approaches for drug development are advantageous due to their fastest predictive ability and cost-effectiveness features. Computer-aided drug design (CADD) techniques utilize different computer programs as well as mathematics formulas to comprehend the interaction of a target and drugs. Traditional methods to determine small-molecule candidates as a drug have several limitations, but CADD utilizes novel methods that require little time and accurately predict a compound against a specific disease with minimal cost.

mathematical modeling CADD QSAR MM-GBSA MM-PBSA pharmacophore modeling MD simulation biological activity drug design

1. Introduction

A drug is a type of natural or synthetic chemical that is used to prevent, treat, or diagnose disease [1]. It can be able to alter the function of a biological system or target from the molecular to the cellular level. Drug discovery helps to determine new therapeutic candidates by using different computational, experimental, and clinical models. The integrated approaches led to the identification of novel drugs not only from plants but also from other chemical sources [2]. Although various therapeutic compounds originating from plant products are highly regarded, synthetic chemistry and biotechnology products account for the majority of medications in the current medical system [3]. The subject of drug development is exceedingly difficult and needs proper infrastructure and laboratory resources. Unfortunately, the traditional strategy of discovering new drug compounds is a time-consuming process that can take up to 10–15 years and can cost up to USD 2.558 billion to bring a therapeutic to market [4]. This is a multistage and complex process that begins with the identification of an appropriate drug target, followed by drug target validation, hit-to-lead identification, and lead molecule optimization, as well as preclinical and clinical research [5]. Despite the huge financial and time commitments required for medication development, clinical trial success is just 13%, with a high drug attrition rate [6].
A mathematical model is a powerful representation of a biological system that uses mathematical ideas and language to produce an accurate description of the system of principles [7]. The model helps in determining the operation process as well as anticipating certain influencing factors and enables the simulation of complex biological processes that generate hypotheses and suggest experiments [8]. The model also known as forecasting modeling is now frequently used to guide drug development at the industrial level. For example, simulation is the more direct approach that utilizes a mathematical model and predicts system behavior under given conditions [9]. Mathematical model-based biological complex system analysis has high productivity and low cost. The process generates novel lead compounds that undergo clinical trials and reach the market [10]. Most of the major obstacles that arose during the conventional drug design and discovery process may be overcome by employing mathematical models [11]. These models are now being utilized in in silico research to describe various pharmacological properties of potential medicinal drugs [12]. For example, the FDA’s Center for Drug Evaluation and Research (CDER) uses modeling and computer simulations at various phases of drug discovery [13].
Currently, CADD has proven to be a useful and powerful strategy in the manufacture of various medicines [14]. The approach has assisted in overcoming the drawbacks of a time-consuming and expensive procedure in drug research and development [15]. In the latest drug design process, the in silico approach is more important than before. CADD methods such as pharmacophore modeling, virtual screening, molecular docking, and dynamic simulation are frequently applied to identify, develop, and evaluate medicinal properties as well as comparable physiological activity of substances [16]. To quantify the binding efficiency and toxicity of a compound in the classical drug development process, massive in vitro and in vivo trials are required [17]. CADD techniques include a molecular docking methodology that can effectively categorize a large number of molecules with higher binding effectiveness [18]. The method can be used to identify the interaction between a ligand and a receptor at the atomic scale, which helps to identify the binding position of a molecular to a target protein and subsequently provides an idea about the biochemical process [19]. The technique also provides information regarding the target behavior and predicts how a protein (enzyme) interacts with small molecules (ligands) at the binding site of target proteins and facilitates the evaluation of the biological activity of a molecular candidate [20]. Additionally, the CADD approaches include different pharmacology properties analysis tools that can evaluate a compound’s pharmacokinetic (PK) parameters such as bioavailability, toxicity, and effectiveness within a short period. Furthermore, the CADD approaches also include molecular dynamics (MD) simulation techniques that can determine a ligand’s binding stability towards its receptor, which is more suitable and accurate [21]. 

2. Target Identification

The early stages of drug discovery probably start with target selection and later move to lead optimization. In the process of potential disease, target discovery is dependent on a variety of resources, involving academic studies, clinical investigations, and the business sector. The pharmaceutical industry, as well as numerous research organizations, use the designated target to locate molecules for developing authorized treatments [22]. Several preliminary stages are involved in this procedure. Throughout the process of target identification and validation, researchers search for chemicals to disrupt a particular biological path that is connected to a certain illness [23]. These compounds can be found in nature, identified through high-throughput screening of large compound libraries, or synthesized as analogs of other drugs that have been proven to be effective against a specific disease. The initial stages in target classification and identification are to determine the function of a possible therapeutic target (which may be a gene or protein) and its involvement in the illness [24]. The molecular processes addressed by the objective are characterized by the following target identification. A good target must always be productive, safe, suitable, and druggable, and it must fulfill clinical and financial requirements. Target identification may be divided into two types: the system biology approach and the molecular biology approach. The system biology approach is a technique that involves studying diseases in complete organisms and selecting targets based on data from clinical trials and in vivo animal research [25]. The molecular biology method, which is at the heart of today’s target identification efforts, aims to find “druggable” targets whose activity may be influenced by associations with molecules, proteins, and sometimes antibodies. Since the biological factors involved in human diseases are so complicated, the foremost essential issue in target identification is not only identifying, optimizing, and choosing trustworthy “druggable” targets, but also truly comprehending the cell membrane associations that identify disease patterns, developing predictive models, and building biological mechanisms for human diseases [26]. For example, G-protein-coupled receptors (GPCRs) and protein kinases are highly “druggable” targets that were identified throughout the molecular biology-based methods [27].
Network-based drug discovery, a field that utilizes information in drug–protein and protein–disease networks, may also be used to study target identification [28]. This strategy entails a highly collaborative scheme between databases and correlations across genomics, transcriptomics, proteomics, metabolomics, the study of the microbiome, and pharmacogenomics, and it is heavily reliant on the development of relevant mathematical, computational, and systems biology tools that connect pharmacological and genomic domains and create computational frameworks for drug target discovery [29]. Another recent network-based application was the combination of large-scale structural genomics and disease association studies to produce a three-dimensional human interactome, which resulted in the identification of candidate genes for previously unknown disease-to-gene associations with proposed molecular mechanisms.

3. Mathematical Models in Drug Design

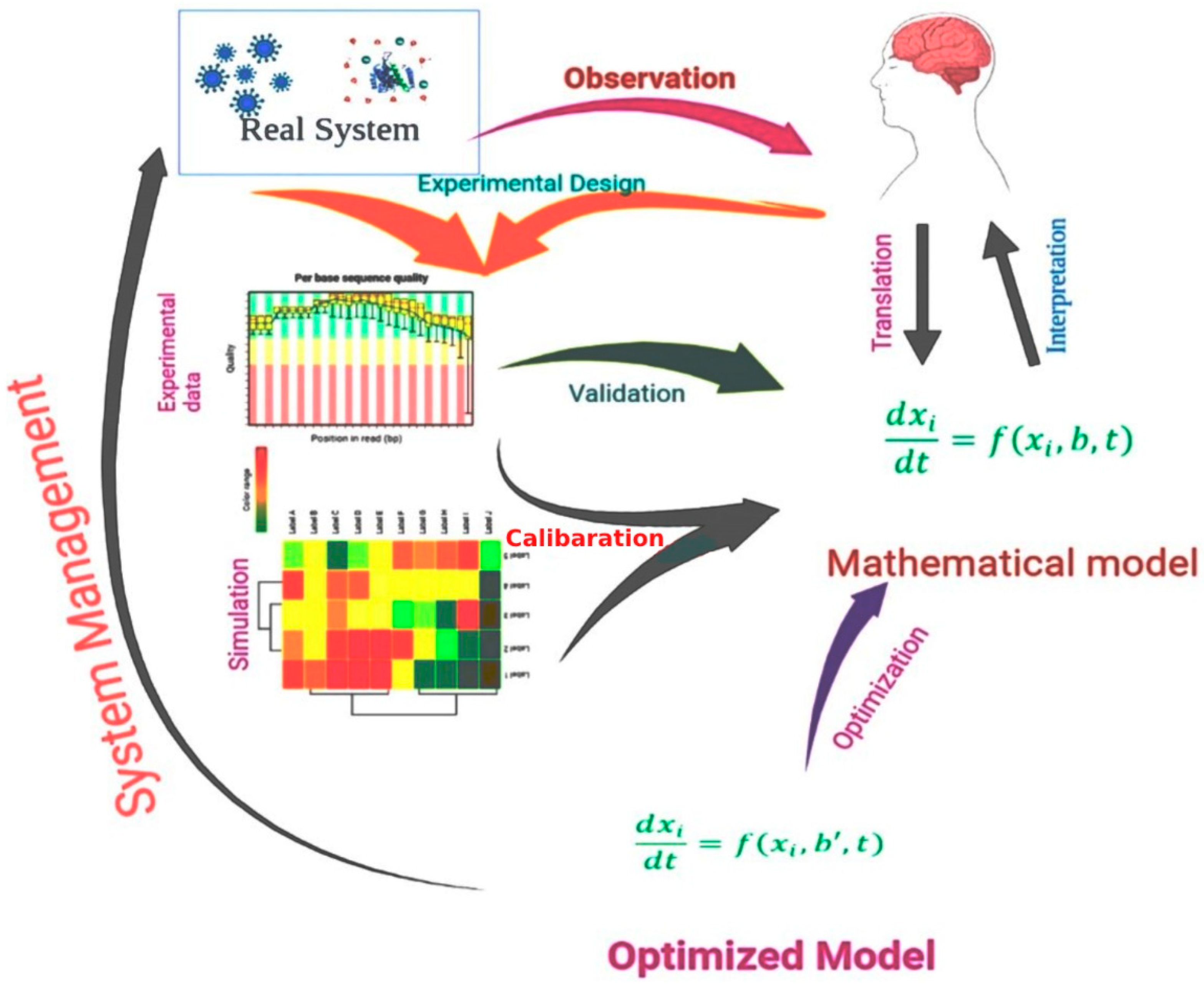
Mathematical techniques for drug discovery have a high value because of their potential effect and low cost compared to preclinical studies [30]. The employment of mathematical models, as well as computer simulations, has several advantages. It can be very helpful for systematically determining the relevance of a specific target or pathway for the overall behavior of the system. First, the inconsistencies between the behavior forecasted by a mathematical model and the behavior observed in actual trials might point to missing components, in which the mathematical model allows for a briefer image of a biological mechanism to develop. Although it is not clear which compounds are absent from the system under review, the mathematical model research findings may be used to influence the construction of additional investigations to address the problem. In addition, mathematical models enable a systematic analysis of system fluctuations triggered by the delivery of drugs [31]. However, it is difficult to represent real-world systems such as biological systems in terms of mathematical relationships [32]. Figure 1 shows the process of the use of a mathematical model in the drug design process.
Figure 1. A schematic representation of a mathematical model, including experimental design, experimental data analysis, model optimization, and model validation, used in modern drug design approaches.
Pharmacokinetic and pharmacodynamic analyses are the earliest and most widely used forms of mathematics in drug design. Pharmacokinetics is the study that describes how drug concentrations change over time, whereas pharmacodynamics explains how drug effects fluctuate with concentration. Pharmacokinetics depict a possible drug’s concentration in the appropriate organ compartments (e.g., circulating blood). Pharmacodynamic models relate this concentration to a biomarker that is thought to be linked with a disease state, often considering the modification of the pharmaceutical target [33].
Cancer research is a good example of how mathematical models are used in drug discovery. One of the most widely employed mathematical models in cancer treatment research is integrated into network-based medicine [34]. Network medicine is a discipline of medicine that explores molecular and physiological links with therapeutic implications. Infectious diseases, such as malaria, are another instance of a mathematical model application in drug innovation [35]. In this situation, mathematical models may be employed to evaluate the prospective drug’s capacity to destroy the parasite at a different phase of the disease. Compound pharmacokinetics and compound pharmacodynamics are used in such models. COVID-19, an infectious viral disease, is the most recent example of how mathematical models are employed in drug discovery [36].

4. Protein Structure Prediction

Proteins are vital molecules that are involved in a variety of biological activities. Protein structure prediction or modeling is critical since a protein’s activity is largely determined by its three-dimensional structure. Furthermore, a protein’s 3D structure is determined by its amino acid composition. 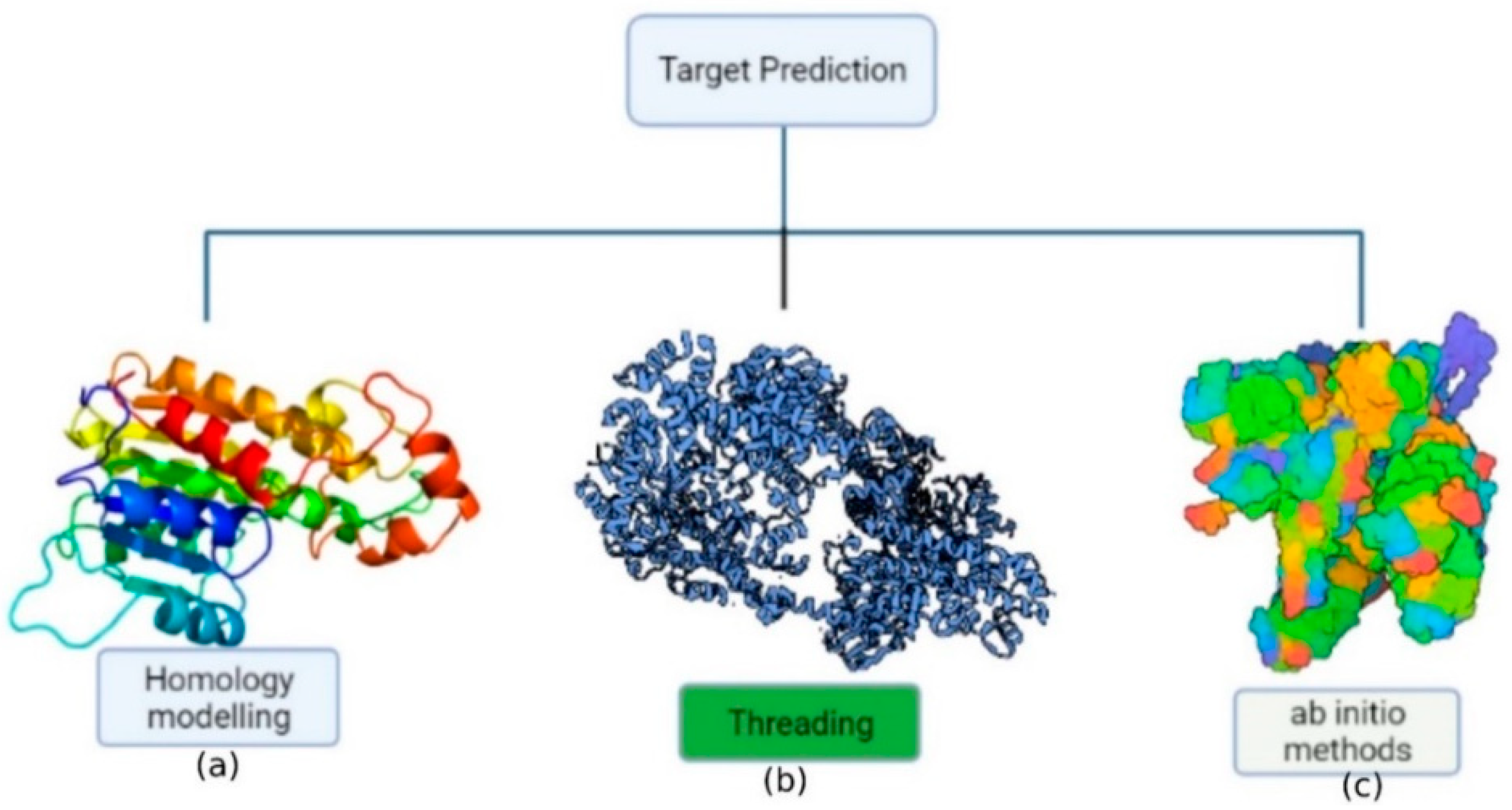Experiments using X-ray crystallography or NMR spectroscopy to resolve protein structure are time-consuming, expensive, and complex [37]. Consequently, theoretical knowledge of protein structure, dynamics, and folding has been used to construct a model from amino acid sequences due to the improvement of computer methods and computational tools. The approaches for predicting protein structure may be divided into three categories (Figure 2): (a) homology modeling; (b) threading; (c) ab initio methods (de novo).
Figure 2. Representation of the protein structure prediction methods: (a) homology-based approach; (b) threading approach; (c) ab initio approach.
The most effective computer technique for protein structure prediction is homology modeling, which involves predicting an unknown structure using a similar known protein structure as a framework [38]. An ideal therapeutic simulation of a protein may be built by assigning a structure based on sequence alignment and then creating the model and minimizing energy. Despite homology modeling’s predictive potential and utility, some issues remain. Firstly, the amounts of target-template architectural conservation and alignment precision are key indicators of the model’s quality. If the identity of the template sequence is below 20%, around 50% of residues inside the layout are likely to be misaligned. Another concern includes that homology modeling systems should develop innovative ways to manage the expanding number of existing protein molecules. To date, different homology modeling tools has been developed and the most frequent use tools use for the modeling has been listed in Table 1.
Threading a sequence throughout a fold involves a precise adjustment of the protein’s amino acid sequence with the folding motif’s corresponding amino acid residue residues. The main goal of this technique is to determine the most possible fold from a given sequence or to find appropriate sequences that might fold into a certain structure. Threading performance is characterized by the number of useable folds whose structures are determined precisely towards the atomic level [39]. Threading processes, which use approaches for aligning sequences with 3D shapes to determine the proper folding of a given sequence from a range of possibilities, were used to make the predictions.
In absence of an experimentally solved structure of a similar/homologous protein, ab initio (de novo) protein structure prediction is a technique for evaluating the three-dimensional structure, when an experimentally solved structure of a similar/homologous protein is not present. The energy function guides the construction of protein structure in this strategy. The ab initio (from scratch) methodologies are based on first-principles physics and chemistry regulations, as well as the premise that a protein’s natural structure always remains at the lowest energy level [40]. However, the precision of ab initio modeling is poor, and performance is generally limited to tiny proteins (120 residues).
Table 1. Summary of the most widely recognized homology modeling tools use in drug development.
No Name Application Availability Reference
1. I-TASSER Reassembling fragment structure via threading https://zhanggroup.org/I-TASSER/ [41]
2. SWISS-MODEL Segment assembly/local similarity https://swissmodel.expasy.org/ [42]
3. ESyPred3D 3D modeling, template identification, and alignment https://www.unamur.be/sciences/biologie/urbm/bioinfo/esypred/ [43]
4. HH-suite Template detection, alignment, 3D modeling https://arquivo.pt/wayback/20160514083149/http:/toolkit.tuebingen.mpg.de/hhpred [44]
5. RaptorX Protein 3D modeling, remote homology discovery, and binding site prediction http://raptorx.uchicago.edu/ [45]
6. FoldX Protein design and energy calculations https://foldxsuite.crg.eu/ [46]
7. ROBETTA Rosetta homology modeling and fragment assembly from scratch with Ginzu domain prediction http://robetta.bakerlab.org/ [47]
8. BHAGEERATH-H Methods of ab initio folding and homology are combined http://www.scfbio-iitd.res.in/bhageerath/bhageerath_h.jsp [48]
9. Prime Homology modeling, evaluation, and refining of the produced model using the energy function https://www.schrodinger.com/prime [49]
10. LOMETS Tertiary structure prediction with a local meta-threading server https://zhanglab.ccmb.med.umich.edu/ [50]

5. Computer-Aided Drug Design

Computer-aided drug design methods have been applied in the field of drug development over the past two decades [51]. Currently, this is seen as one of the best appropriate alternatives to high-throughput screening, which is routinely used in drug design and development. CADD may be used for all efforts that have been made throughout the process of drug development that can be described mathematically and analyzed using numerical methods [52]. 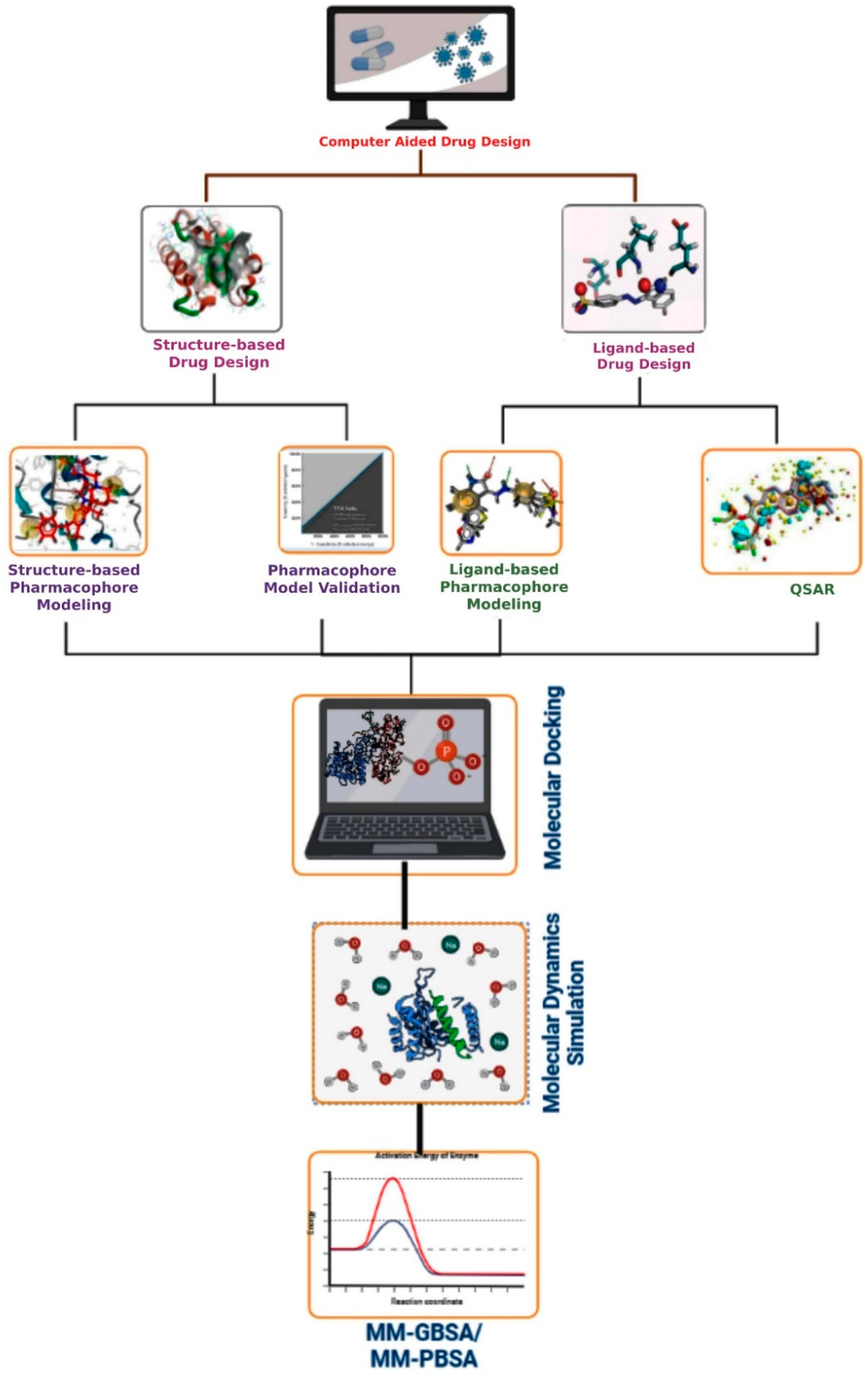Figure 3 demonstrates the basic CADD approach that may be utilized interactively with experimental methodologies to find novel drug targets and direct iterative ligand optimization. Structure-based and ligand-based drug design techniques are two types of CADD that have been widely used throughout the development of drugs process to find acceptable lead compounds. The CADD approaches help to expedite the drug discovery and development process by minimizing the cost and time [53]. However, if the computer system crashes unexpectedly, the CADD designs might be lost. If proper precautions are not performed, viruses will infect the computer system.
Figure 3. Representation of the basic workflow of computational drug design approaches. The CADD approaches include structure- and ligand-based drug design approaches, pharmacophore modeling, virtual screening, molecular docking, ADMET, dynamics simulation, and MM-GBSA or MM-PBSA approaches.

5.1. Structure-Based Drug Design

Structure-based drug design (SBDD) (or direct techniques) can be used if the target’s spatial structure is available. Compounds with qualities complementary to the target area can be created based on the properties and features of the macromolecule’s spatial structure. X-ray crystallography, NMR, and in silico homology-based prediction approaches can all be used to determine a protein’s 3D structure. The protein’s binding/active site is discovered when the three-dimensional structure is understood. Structure-based pharmacophore modeling, virtual screening (SBVS), molecular docking, and molecular dynamics (MD) simulations are some of the typical methodologies used in SBDD.

5.1.1. Structure-Based Pharmacophore Modeling

The pharmacophore features are discovered by utilizing the shape of the complicated molecular target [54]. The characteristics are founded on a single X-ray crystallized target–ligand complex. The pharmacophore characteristics are built using a single ligand as well as its associations with the specific target protein. The fundamental contrast between ligand-based and structure-based approaches is the number of ligands utilized to construct the pharmacophore. The ligand-based technique necessitates at least 30 actives, whereas the structure-based method necessitates only one ligand and its connection with the receptor. Furthermore, the pharmacophore technique is derived from an active site of the ligand. Another method for creating a structure-based pharmacophore is to employ an APO template in such a way that the active site amino acids are determined and then develop a feature list based on their interaction properties that may be included in the pharmacophore [55]. The only drawback is when the list predicts too many features (more than seven features).

5.1.2. Pharmacophore Model Validation

Structure-based pharmacophore modeling can be employed efficiently when there is inadequate information on ligands that have been empirically proven to inhibit or stimulate the activity of a certain therapeutic target [56]. Validation is required to obtain an accurate pharmacophore analysis and to analyze the molecular model’s quality. Pharmacophore methods focused on appropriate correlation coefficients (R) might be validated in three main steps: Fisher’s randomization test, test set prediction, and Guner–Henry (GH) scoring technique.

Fisher’s Randomization Test

Fisher’s randomization approach is critical for establishing a link between structural and biological functionality in training set molecules [57]. The relevant experimental data linked with the training dataset are randomly changed to make them statistically irrelevant. The randomized dataset is then used to construct assumptions using the same characteristics and variables that were used to develop the original hypothesis. This randomization approach validated the drug-tested pharmacophore hypothesis by selecting 95% confidence levels, which resulted in 19 random spreadsheets. The randomized dataset should give equivalent or higher cost values, improved RMSD, and significant correlations for successful pharmacophore development.

Test Set Prediction

The goal of the pharmacophore method is to anticipate not only the behavior of molecules in the training dataset, but also the activity of external molecules. The correlation value between the experimental and forecasted behavior of external molecules that were excluded from the training dataset was predicted using test set prediction. This metric determines the predictability of pharmacophores’ stability (free of errors). In this technique, the behavior of the test set components has a higher correlation coefficient, which has a 95% confidence level [58].

5.2. Ligand-Based Drug Design

Ligand-based drug design is considered an indirect technique because the structure of the biomolecular target is unknown and cannot be anticipated using approaches such as homology modeling [59]. The most significant and highly used methods in ligand-based drug discovery are 3D quantitative structure–activity relationships (3D QSARs) and pharmacophore modeling, both of which can supply vital knowledge regarding the nature of connections between drug targets and ligand compounds as well as computer simulations suitable for lead compound optimization [60]. The most crucial aspects of the interaction nature are preserved, but the noise of extra information is eliminated.

5.2.1. Quantitative Structure–Activity Relationship (QSAR) Models

Structure–activity analysis relationship models depict the overall mathematical relationship between a collection of chemicals’ structural properties and target response [61]. The QSAR model has been successfully employed to decrease the need for time-consuming, arduous, and expensive processes in innovative drug development during the last few decades, and it also performed well in terms of predicting physiochemical properties (Table 2). Regression techniques, artificial neural networks, principal component analysis (PCA), and partial least squares (PLS) can be used to determine these correlations. Multiple linear regression is a frequently used approach for establishing a link between active and multiple structural features. When a high number of structural features must be taken into account (for example, grid-based approaches in 3D QSAR), linear regression fails and a specialized method such as PCA or PLS is needed. The idea of multidimensional QSAR has been proposed in recent years [62]. Predicting the biological properties of chemical substances is more beneficial. HQSAR, G-QSAR, MIA-QSAR, and multitarget QSAR are all part of this process, which has had outstanding success in the new drug process. The two most essential methodologies suggested for developing pharmacological compounds are comparative molecular field analysis (CoMFA) and comparative molecular similarity indices analysis (CoMSIA). However, QSAR modeling has some limitations; for example, if the number of molecules in the training set is small, the data may not accurately reflect all of the properties, and therefore it cannot be used to forecast the most active compounds.
Table 2. A list of techniques and mathematical equations used in QSAR modeling as well as drug design.
No Techniques Equation Activity Reference
1. K-nearest neighbor Linear Simple [63]
2. Multiple linear regression Linear Simple [64]
3. Partial least squares Linear Performs effectively on data including a big dataset [65]
4. Artificial neural network Nonlinear Works well with nonlinear data [66]
5. Support vector machine Nonlinear A most effective approach for classification and regression [67]
6. Decision tree Nonlinear Extremely interpretable [68]
7. Random forest Nonlinear A better and more reliable estimate [69]
 

References

  1. Atanasov, A.G.; Zotchev, S.B.; Dirsch, V.M.; Orhan, I.E.; Banach, M.; Rollinger, J.M.; Barreca, D.; Weckwerth, W.; Bauer, R.; Bayer, E.A.; et al. Natural Products in Drug Discovery: Advances and Opportunities. Nat. Rev. Drug Discov. 2021, 20, 200–216.
  2. Atanasov, A.G.; Waltenberger, B.; Pferschy-Wenzig, E.M.; Linder, T.; Wawrosch, C.; Uhrin, P.; Temml, V.; Wang, L.; Schwaiger, S.; Heiss, E.H.; et al. Discovery and Resupply of Pharmacologically Active Plant-Derived Natural Products: A Review. Biotechnol. Adv. 2015, 33, 1582–1614.
  3. Li, C.Q.; Lei, H.M.; Hu, Q.Y.; Li, G.H.; Zhao, P.J. Recent Advances in the Synthetic Biology of Natural Drugs. Front. Bioeng. Biotechnol. 2021, 9, 640.
  4. Rudrapal, M.; Khairnar, S.J.; Jadhav, A.G. Drug Repurposing (DR): An Emerging Approach in Drug Discovery. Drug Repurposing—Hypothesis Mol. Asp. Ther. Appl. 2020.
  5. Hughes, J.P.; Rees, S.S.; Kalindjian, S.B.; Philpott, K.L. Principles of Early Drug Discovery. Br. J. Pharmacol. 2011, 162, 1239–1249.
  6. Dimasi, J.A.; Feldman, L.; Seckler, A.; Wilson, A. Trends in Risks Associated with New Drug Development: Success Rates for Investigational Drugs. Clin. Pharmacol. Ther. 2010, 87, 272–277.
  7. Bajuri, M.R.; Siri, Z.; Abdullah, M.N.S. Mathematical Modeling Research Output Impacting New Technological Development: An Axiomatization to Build Novelty. Axioms 2022, 11, 264.
  8. Ganusov, V.V. Strong Inference in Mathematical Modeling: A Method for Robust Science in the Twenty-First Century. Front. Microbiol. 2016, 7, 1131.
  9. Vlachakis, D.; Vlamos, P. Mathematical Multidimensional Modelling and Structural Artificial Intelligence Pipelines Provide Insights for the Designing of Highly Specific AntiSARS-CoV2 Agents. Math. Comput. Sci. 2021.
  10. Lu, R.M.; Hwang, Y.C.; Liu, I.J.; Lee, C.C.; Tsai, H.Z.; Li, H.J.; Wu, H.C. Development of Therapeutic Antibodies for the Treatment of Diseases. J. Biomed. Sci. 2020, 27, 1–30.
  11. Kohen, Z.; Orenstein, D. Mathematical Modeling of Tech-Related Real-World Problems for Secondary School-Level Mathematics. Educ. Stud. Math. 2021, 107, 71–91.
  12. Ekins, S.; Mestres, J.; Testa, B. In Silico Pharmacology for Drug Discovery: Methods for Virtual Ligand Screening and Profiling. Br. J. Pharmacol. 2007, 152, 9–20.
  13. Bai, J.P.F.; Earp, J.C.; Florian, J.; Madabushi, R.; Strauss, D.G.; Wang, Y.; Zhu, H. Quantitative Systems Pharmacology: Landscape Analysis of Regulatory Submissions to the US Food and Drug Administration. CPT Pharmacomet. Syst. Pharmacol. 2021, 10, 1479–1484.
  14. Macalino, S.J.Y.; Gosu, V.; Hong, S.; Choi, S. Role of Computer-Aided Drug Design in Modern Drug Discovery. Arch. Pharm. Res. 2015, 38, 1686–1701.
  15. Selvaraj, C.; Chandra, I.; Singh, S.K. Artificial Intelligence and Machine Learning Approaches for Drug Design: Challenges and Opportunities for the Pharmaceutical Industries. Mol. Divers. 2021, 1, 1–21.
  16. Opo, F.A.D.M.; Rahman, M.M.; Ahammad, F.; Ahmed, I.; Bhuiyan, M.A.; Asiri, A.M. Structure Based Pharmacophore Modeling, Virtual Screening, Molecular Docking and ADMET Approaches for Identification of Natural Anti-Cancer Agents Targeting XIAP Protein. Sci. Rep. 2021, 11, 1–17.
  17. Shaker, B.; Ahmad, S.; Lee, J.; Jung, C.; Na, D. In Silico Methods and Tools for Drug Discovery. Comput. Biol. Med. 2021, 137, 104851.
  18. Bender, B.J.; Gahbauer, S.; Luttens, A.; Lyu, J.; Webb, C.M.; Stein, R.M.; Fink, E.A.; Balius, T.E.; Carlsson, J.; Irwin, J.J.; et al. A Practical Guide to Large-Scale Docking. Nat. Protoc. 2021, 16, 4799–4832.
  19. Trabelsi, S.; Issaoui, N.; Brandán, S.A.; Bardak, F.; Roisnel, T.; Atac, A.; Marouani, H. Synthesis and Physic-Chemical Properties of a Novel Chromate Compound with Potential Biological Applications, Bis(2-Phenylethylammonium) Chromate(VI). J. Mol. Struct. 2019, 1185, 168–182.
  20. Nawaz, M.Z.; Attique, S.A.; Ain, Q.; Alghamdi, H.A.; Bilal, M.; Yan, W.; Zhu, D. Discovery and Characterization of Dual Inhibitors of Human Vanin-1 and Vanin-2 Enzymes through Molecular Docking and Dynamic Simulation-Based Approach. Int. J. Biol. Macromol. 2022, 213, 1088–1097.
  21. Samad, A.; Ahammad, F.; Nain, Z.; Alam, R.; Imon, R.R.; Hasan, M.; Rahman, M.S. Designing a Multi-Epitope Vaccine against SARS-CoV-2: An Immunoinformatics Approach. J. Biomol. Struct. Dyn. 2020, 1–17.
  22. Payne, D.J.; Gwynn, M.N.; Holmes, D.J.; Pompliano, D.L. Drugs for Bad Bugs: Confronting the Challenges of Antibacterial Discovery. Nat. Rev. Drug Discov. 2007, 6, 29–40.
  23. Gerry, C.J.; Schreiber, S.L. Chemical Probes and Drug Leads from Advances in Synthetic Planning and Methodology. Nat. Rev. Drug Discov. 2018, 17, 333–352.
  24. Furuhashi, M.; Hotamisligil, G.S. Fatty Acid-Binding Proteins: Role in Metabolic Diseases and Potential as Drug Targets. Nat. Rev. Drug Discov. 2008, 7, 489–503.
  25. Eckhardt, M.; Hultquist, J.F.; Kaake, R.M.; Hüttenhain, R.; Krogan, N.J. A Systems Approach to Infectious Disease. Nat. Rev. Genet. 2020, 21, 339–354.
  26. Nogales, C.; Mamdouh, Z.M.; List, M.; Kiel, C.; Casas, A.I.; Schmidt, H.H.H.W. Network Pharmacology: Curing Causal Mechanisms Instead of Treating Symptoms. Trends Pharmacol. Sci. 2022, 43, 136–150.
  27. Yang, D.; Zhou, Q.; Labroska, V.; Qin, S.; Darbalaei, S.; Wu, Y.; Yuliantie, E.; Xie, L.; Tao, H.; Cheng, J.; et al. G Protein-Coupled Receptors: Structure- and Function-Based Drug Discovery. Signal Transduct. Target. Ther. 2021, 6, 1–27.
  28. Zhao, L.; Zhu, Y.; Wang, J.; Wen, N.; Wang, C.; Cheng, L. A Brief Review of Protein–Ligand Interaction Prediction. Comput. Struct. Biotechnol. J. 2022, 20, 2831–2838.
  29. Choudhary, K.; DeCost, B.; Chen, C.; Jain, A.; Tavazza, F.; Cohn, R.; Park, C.W.; Choudhary, A.; Agrawal, A.; Billinge, S.J.L.; et al. Recent Advances and Applications of Deep Learning Methods in Materials Science. NPJ Comput. Mater. 2022, 8, 59.
  30. Lin, X.; Li, X.; Lin, X. A Review on Applications of Computational Methods in Drug Screening and Design. Molecules 2020, 25, 1375.
  31. Marino, S.; Baxter, N.T.; Huffnagle, G.B.; Petrosino, J.F.; Schloss, P.D. Mathematical Modeling of Primary Succession of Murine Intestinal Microbiota. Proc. Natl. Acad. Sci. USA 2014, 111, 439–444.
  32. Demers, J.; Robertson, S.L.; Bewick, S.; Fagan, W.F. Implicit versus Explicit Vector Management Strategies in Models for Vector-Borne Disease Epidemiology. J. Math. Biol. 2022, 84, 1–32.
  33. Kantae, V.; Krekels, E.H.J.; Esdonk, M.J.V.; Lindenburg, P.; Harms, A.C.; Knibbe, C.A.J.; Van der Graaf, P.H.; Hankemeier, T. Integration of Pharmacometabolomics with Pharmacokinetics and Pharmacodynamics: Towards Personalized Drug Therapy. Metabolomics 2017, 13, 1–11.
  34. Sun, X.; Hu, B. Mathematical Modeling and Computational Prediction of Cancer Drug Resistance. Brief. Bioinform. 2017, 19, 1382–1399.
  35. Mandal, S.; Sarkar, R.; Sinha, S. Mathematical Models of Malaria—A Review. Malar. J. 2011, 10, 1–19.
  36. Alam, R.; Imon, R.R.; Kabir Talukder, M.E.; Akhter, S.; Hossain, M.A.; Ahammad, F.; Rahman, M.M. GC-MS Analysis of Phytoconstituents FromRuellia ProstrataandSenna Toraand Identification of Potential Anti-Viral Activity against SARS-CoV-2. RSC Adv. 2021, 11, 40120–40135.
  37. Heikkinen, H.A.; Backlund, S.M.; Iwaï, H. Nmr Structure Determinations of Small Proteins Using Only One Fractionally 20%13 C-and Uniformly 100%15 n-Labeled Sample. Molecules 2021, 26, 747.
  38. Jumper, J.; Evans, R.; Pritzel, A.; Green, T.; Figurnov, M.; Ronneberger, O.; Tunyasuvunakool, K.; Bates, R.; Žídek, A.; Potapenko, A.; et al. Highly Accurate Protein Structure Prediction with AlphaFold. Nature 2021, 596, 583–589.
  39. Marshall, G.R.; Taylor, C.M. Introduction to Computer-Assisted Drug Design—Overview and Perspective for the Future. In Comprehensive Medicinal Chemistry II; Elsevier Ltd.: Amsterdam, The Netherlands, 2006; Volume 4, pp. 13–41. ISBN 9780080450445.
  40. Dill, K.A.; Ozkan, S.B.; Shell, M.S.; Weikl, T.R. The Protein Folding Problem. Annu. Rev. Biophys. 2008, 37, 289–316.
  41. Yang, J.; Yan, R.; Roy, A.; Xu, D.; Poisson, J.; Zhang, Y. The I-TASSER Suite: Protein Structure and Function Prediction. Nat. Methods 2014, 12, 7–8.
  42. Guex, N.; Peitsch, M.C. SWISS-MODEL and the Swiss-PdbViewer: An Environment for Comparative Protein Modeling. Electrophoresis 1997, 18, 2714–2723.
  43. Lambert, C.; Léonard, N.; De Bolle, X.; Depiereux, E. ESyPred3D: Prediction of Proteins 3D Structures. Bioinformatics 2002, 18, 1250–1256.
  44. Steinegger, M.; Meier, M.; Mirdita, M.; Vöhringer, H.; Haunsberger, S.J.; Söding, J. HH-Suite3 for Fast Remote Homology Detection and Deep Protein Annotation. BMC Bioinform. 2019, 20, 1–15.
  45. Källberg, M.; Wang, H.; Wang, S.; Peng, J.; Wang, Z.; Lu, H.; Xu, J. Template-Based Protein Structure Modeling Using the RaptorX Web Server. Nat. Protoc. 2012, 7, 1511–1522.
  46. Schymkowitz, J.; Borg, J.; Stricher, F.; Nys, R.; Rousseau, F.; Serrano, L. The FoldX Web Server: An Online Force Field. Nucleic Acids Res. 2005, 33, W382–W388.
  47. Kim, D.E.; Chivian, D.; Baker, D. Protein Structure Prediction and Analysis Using the Robetta Server. Nucleic Acids Res. 2004, 32, W526–W531.
  48. Jayaram, B.; Dhingra, P.; Mishra, A.; Kaushik, R.; Mukherjee, G.; Singh, A.; Shekhar, S. Bhageerath-H: A Homology/Ab Initio Hybrid Server for Predicting Tertiary Structures of Monomeric Soluble Proteins. BMC Bioinform. 2014, 15, 1–12.
  49. Chi, P.; Li, S.; Xu, C.; Zhang, T.; Zhao, J.; Liu, Y.; Wang, Y.; Xie, Y. PRIME: A Novel Processing-in-Memory Architecture for Neural Network Computation in ReRAM-Based Main Memory. In Proceedings of the Proceedings—2016 43rd International Symposium on Computer Architecture, ISCA 2016, Seoul, Korea, 18–22 June 2016; Volume 44, pp. 27–39.
  50. Wu, S.; Zhang, Y. LOMETS: A Local Meta-Threading-Server for Protein Structure Prediction. Nucleic Acids Res. 2007, 35, 3375–3382.
  51. Zhang, T.; Huang, Z.; Wang, Y.; Wen, C.; Peng, Y.; Ye, Y. Information Extraction from the Text Data on Traditional Chinese Medicine: A Review on Tasks, Challenges, and Methods from 2010 to 2021. Evidence-Based Complement. Altern. Med. 2022, 2022, 1679589.
  52. Ou-Yang, S.S.; Lu, J.Y.; Kong, X.Q.; Liang, Z.J.; Luo, C.; Jiang, H. Computational Drug Discovery. Acta Pharmacol. Sin. 2012, 33, 1131–1140.
  53. Ahammad, F.; Alam, R.; Mahmud, R.; Akhter, S.; Talukder, E.K.; Tonmoy, A.M.; Fahim, S.; Al-Ghamdi, K.; Samad, A.; Qadri, I. Pharmacoinformatics and Molecular Dynamics Simulation-Based Phytochemical Screening of Neem Plant (Azadiractha Indica) against Human Cancer by Targeting MCM7 Protein. Brief. Bioinform. 2021, 22, bbab098.
  54. Santos-Filho, A.; Giordano, D.; Biancaniello, C.; Argenio, M.A.; Facchiano, A. Drug Design by Pharmacophore and Virtual Screening Approach. Pharmaceuticals 2022, 15, 646.
  55. Ferreira, L.G.; Dos Santos, R.N.; Oliva, G.; Andricopulo, A.D. Molecular Docking and Structure-Based Drug Design Strategies. Molecules 2015, 20, 13384–13421.
  56. Cheng, T.; Li, Q.; Zhou, Z.; Wang, Y.; Bryant, S.H. Structure-Based Virtual Screening for Drug Discovery: A Problem-Centric Review. AAPS J. 2012, 14, 133–141.
  57. Gaurav, A.; Gautam, V. Pharmacophore Based Virtual Screening Approach to Identify Selective PDE4B Inhibitors. Iran. J. Pharm. Res. 2017, 16, 910–923.
  58. Watson, P.F.; Petrie, A. Method Agreement Analysis: A Review of Correct Methodology. Theriogenology 2010, 73, 1167–1179.
  59. Aparoy, P.; Kumar Reddy, K.; Reddanna, P. Structure and Ligand Based Drug Design Strategies in the Development of Novel 5- LOX Inhibitors. Curr. Med. Chem. 2012, 19, 3763–3778.
  60. Alberto, A.V.P.; da Silva Ferreira, N.C.; Soares, R.F.; Alves, L.A. Molecular Modeling Applied to the Discovery of New Lead Compounds for P2 Receptors Based on Natural Sources. Front. Pharmacol. 2020, 11, 1221.
  61. Neves, B.J.; Braga, R.C.; Melo-Filho, C.C.; Moreira-Filho, J.T.; Muratov, E.N.; Andrade, C.H. QSAR-Based Virtual Screening: Advances and Applications in Drug Discovery. Front. Pharmacol. 2018, 9, 1275.
  62. Myint, K.Z.; Xie, X.Q. Recent Advances in Fragment-Based QSAR and Multi-Dimensional QSAR Methods. Int. J. Mol. Sci. 2010, 11, 3846–3866.
  63. Peterson, L. K-Nearest Neighbor. Scholarpedia 2009, 4, 1883.
  64. Uyanık, G.K.; Güler, N. A Study on Multiple Linear Regression Analysis. Procedia Soc. Behav. Sci. 2013, 106, 234–240.
  65. Rosipal, R.; Krämer, N. Overview and Recent Advances in Partial Least Squares. In Proceedings of the Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2006; Volume 3940 LNCS, pp. 34–51.
  66. Abiodun, O.I.; Jantan, A.; Omolara, A.E.; Dada, K.V.; Mohamed, N.A.E.; Arshad, H. State-of-the-Art in Artificial Neural Network Applications: A Survey. Heliyon 2018, 4, e00938.
  67. Noble, W.S. What Is a Support Vector Machine? Nat. Biotechnol. 2006, 24, 1565–1567.
  68. Myles, A.J.; Feudale, R.N.; Liu, Y.; Woody, N.A.; Brown, S.D. An Introduction to Decision Tree Modeling. J. Chemom. 2004, 18, 275–285.
  69. Belgiu, M.; Drăgu, L. Random Forest in Remote Sensing: A Review of Applications and Future Directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Biophysics; Others
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Md Rifat Hasan
,
Ahad Amer Alsaiari
,
Burhan Zain Fakhurji
,
Mohammad Habibur Rahman Molla
,
Amer H. Asseri
,
Md Afsar Ahmed Sumon
,
Moon Nyeo Park
,
Foysal Ahammad
,
Bonglee Kim
View Times: 3.4K
Entry Collection: Biopharmaceuticals Technology
Revisions: 3 times (View History)
Update Date: 01 Aug 2022
Table of Contents
    1000/1000
    Hot Most Recent
    Feedback