State of Charge Estimation Techniques for EV Applications

Version	Summary	Created by	Modification	Content Size	Created at	Operation
1		T GIRIJA PRASANNA	--	3101	2022-06-24 07:35:26	\|
2	format	Jason Zhu	-59 word(s)	3042	2022-06-24 09:39:13	\|

This entry is adapted from the peer-reviewed paper 10.3390/electronics11111795

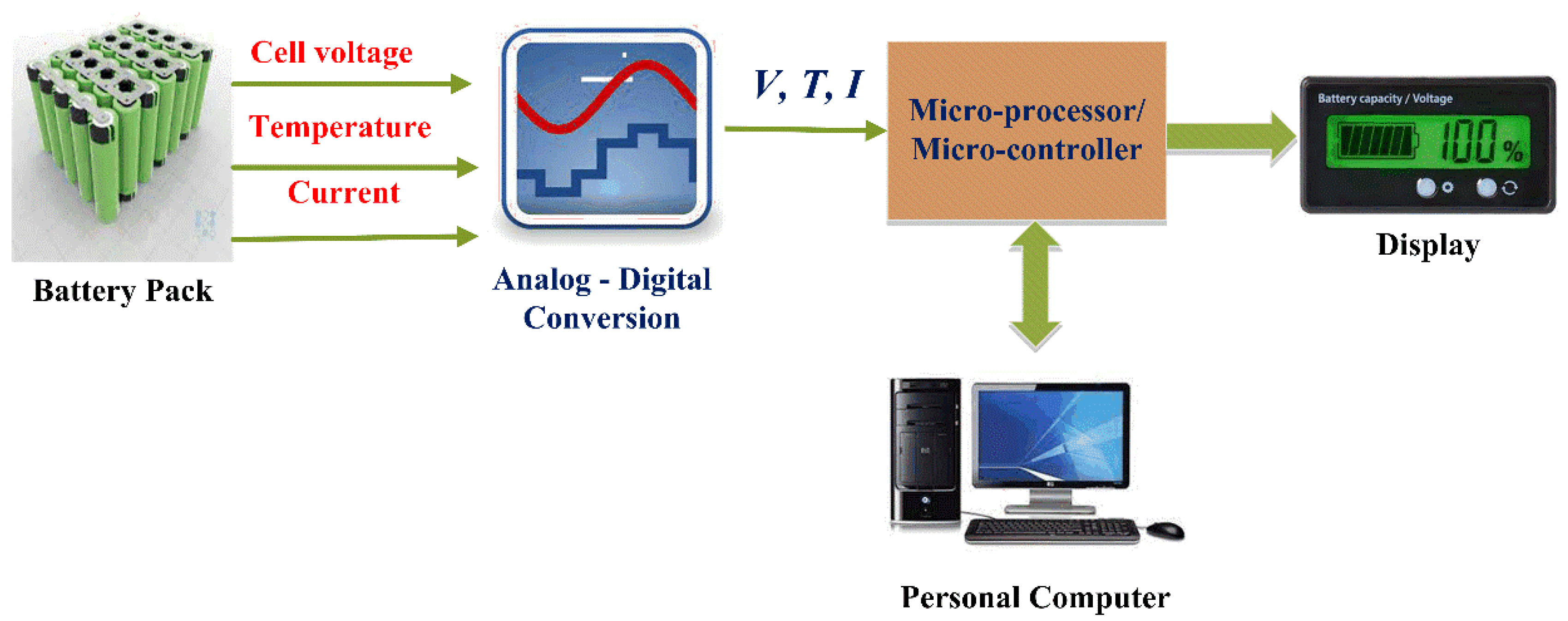
Electric vehicles (EVs) have acquired significant popularity due to their performance and efficiency. EVs are already largely acknowledged as the most promising solutions to global environmental challenges and CO₂ emissions. Li-ion batteries are most frequently employed in EVs due to their various benefits. An effective Battery Management System (BMS) is essential to improve the battery's- performance, including charging-discharging control, precise monitoring, heat management, battery safety, and protection, and also an accurate estimation of the State of Charge (SOC). The SOC is required to provide the driver with a precise indication of the remaining range.

Electric vehicles State of Charge Adaptive Filter Algorithm Li-ion battery Estimation Techniques

1. Introduction

There has been a significant worry for all energy-storing devices for state of charge (SOC) estimation. SOC estimation gives researchers data and estimates the reliability of batteries with high precision. Since the 1980s, numerous methods have been introduced to estimate SOC. Although SOC estimation is a crucial challenge in EV batteries, it cannot be measured directly. It requires a specific algorithm for describing the battery’s remaining capacity. The general architecture of the SOC system is shown in Figure 1. For SOC estimation, the current integration is the most traditional technique. The ratio of the available capacity to the battery’s total capacity is shown in Equation.

where i indicates the current of the battery and c_m indicates the total capacity.

/media/item_content/202206/62b569320fbaeelectronics-11-01795-g006.png

Figure 1. The general architecture of the SOC system.

The battery’s total capacity decreases gradually due to its internal reaction and external load, leading to its nonlinear and non-stationary degradation characteristics. The categorization of SOC estimation methods is shown in Figure 2. Different kinds of literature have been presented in various manners. Every technique has its unique advantages along with disadvantages. SOC estimation methods were divided into five types: conventional, adaptive filter, learning algorithms, nonlinear observers, and others. Again, each process was classified into sub-methods ^[1], described as follows.

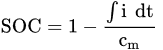
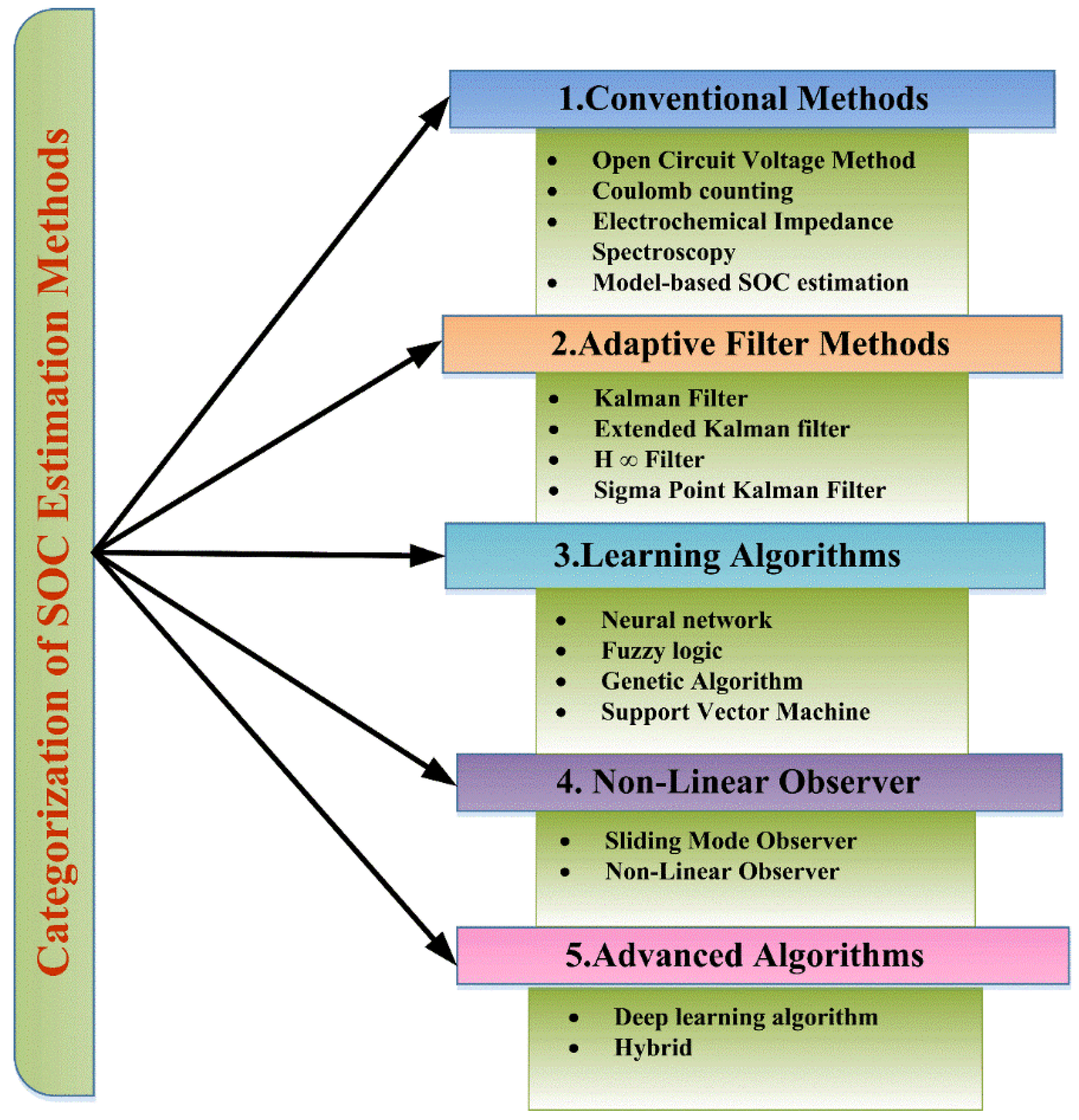
/media/item_content/202206/62b5694b85b7aelectronics-11-01795-g007.png

Figure 2. Categorization of methods for estimation of SOC.

2. Conventional Methods

2.1. Open-Circuit Voltage Method

The open-circuit voltage method has high accuracy, is easy to implement, and is a straightforward method, but its main disadvantage is that it takes more time to reach an equilibrium position. Therefore, online estimation of SOC is not an appropriate method. Therefore, this method is applicable only for low power consumption applications. Moreover, some observations are required to measure the discharge and charge voltage. For example, at high OCV, the battery is charged, and it is discharged at small OCV because of the hysteresis characteristics in batteries ^[2]^[3]^[4]^[5].

2.2. Coulomb Counting (CC) Method

The CC technique is the easiest one to estimate the SOC of the battery, and it can be implemented very quickly with low power calculation. The charging/discharging of the battery depends upon the integration of the current concerning time. It is expressed in Equation.

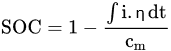
where $η$ indicates the Coulombic efficiency, $i$ indicates the current of the battery, and $c_{m}$

indicates the total capacity.

However, due to its uncertain disturbances, noise, temperature, and current, its results could be inaccurate. Furthermore, more difficulties exist in determining the SOC initial values, which might cause a cumulative error ^[6]. Additionally, to attain the maximum capacity, this method needs periodic capacity and complete cell discharge, which shortens the battery’s lifespan ^[7].

2.3. Electrochemical Impedance Spectroscopy (EIS)

To implement the EIS, an appropriate electrochemical model is needed. Then, it evaluates the battery impedance by using capacitances and inductances over an extensive range of frequencies ^[8]^[9]^[10] that are recognized in an equivalent circuit model that includes two capacitive arcs and an inductive arc operated at low and high frequencies. Under various SOC values, a nonlinear LSF technique is utilized for computing the model impedances. If the system is not functioning in stable conditions, the EIS outcomes are difficult to reproduce. It has the advantages of low cost, operating online, and attaining good accuracy. From the actual values, the effect of battery temperature and the aging difference could vary the estimated outcomes, resulting in a deficiency of precision.

2.4. Model-Based SOC Estimation

Since the open-circuit voltage scheme cannot execute online, it needs appropriate rest time to monitor the SOC, which means it cannot be applied while the vehicle moves. Therefore, for online SOC, battery model development is essential. The most used battery models include the electrochemical ^[11]^[12]^[13]^[14]^[15] and equivalent circuit models ^[16]^[17]. An electrochemical model is used to study the battery’s performance, which relates to the internal materials and considers the chemical thermodynamics and the electrodynamics effect. It can be expressed as:

where V denotes the terminal voltage, VOC means open-circuit voltage, VR indicates the potential difference across resistance, and VP represents the electric potential.

The RC networks have been used for the equivalent circuit model by considering dynamic and polarization characteristics. Using RLS (recursive least square) algorithm, the online OCV is executed and, for various RC networks, the outcome of the RLS algorithm is compared with experimental results. A model-based estimation is used online, and it has high precision. The drawback of this method for the specific battery is that a complete explanation of the electrochemical reactions is required, and it highly depends on the model’s accuracy.

3. Adaptive Filter (AF) Algorithm

3.1. Kalman Filter (KF) Algorithm

KF is a well-designed and intelligent tool commonly used in automobiles, navigator tracking, and aerospace applications. The striking feature of the Kalman filter is it has a self-correcting nature. A Kalman filter linear model contains a state equation, which predicts the current state, and a measurement equation, which updates the current state ^[18], which are expressed as follows:

where A, B, C, and D represent the covariance matrices, x is the system state, f represents the process noise, u represents the control input, y represents the measurement input, and z represents measurement noise. Ting et al. ^[19] developed an RC battery model, which is used for modeling a Kalman filter. To explain the dynamic battery characteristics, the RC model mathematical equations remain converted into a state–space model to describe the dynamic battery characteristics. The outcome indicates that the estimated RMS error of the SOC using the Kalman filter is minor compared to the measured error. The researchers of ^[20] also used the same method on the electrical equivalent model of a Li-ion battery with the help of the dSPACE real-time card and Matlab/Simulink software. The estimated SOC error was less than 5%. Yatsui ^[21] combined the results of a Kalman filter with two methods, the OCV, and the CC methods, to ameliorate the non-ideal factors. After executing the Kalman filter, the SOC precision was improved, with an error of ±1.76%. However, the Kalman filter cannot be used directly. It needs a complex calculation and is profoundly dependable with great strength to various working conditions and battery aging. On the other hand, MI-UKF is impervious to unanticipated operational requirements and can improve UKF accuracy by more than 1% ^[22]^[23]^[24].

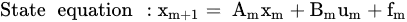
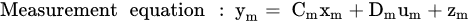
3.2. Extended Kalman Filter (EKF)

EKF has been applied to work the framework in nonlinear applications. It uses first-order Taylor series expansion and partial derivatives to linearize the battery model. At every instant of time, the state-space model is linearized and equates the predicted value of the battery with the measured voltage to precisely approximate the constraints for the SOC. If the scheme is exceptionally nonlinear, a linearization blunder might still happen. In any case, the linearization blunder could happen when the framework is profoundly nonlinear since the first-order Taylor series experiences an absence of precision in an exceptionally nonlinear state. Finally, the improved dual AEKF algorithm was applied, and the SOH and SOC estimation errors were within 1% ^[25]^[26]^[27]^[28]^[29]^[30]^[31]^[32].

3.3. H ∞ Filter

This is a very simple method in the designed model, and it does not have to know any details and measurement characteristics of noise. It considers only the time-varying parameters of the battery to carry out the system under the specific condition, which has robust strength. The precision of the model is deviated due to hysteresis, aging, and temperature effects ^[33]^[34]^[35]^[36]. In ^[37], this method was introduced to estimate battery SOC. The time-varying parameters are current, SOH, and temperature for second-order RC filter circuit design. An HPPC (hybrid pulse power characterization) experiment was performed to extract the voltage, resistance, and present characteristics. The projected model was tested using six Urban Dynamometer Driving Schedule tests and attained a good accuracy. In ^[38], the adaptive H∞ filter was introduced to estimate SOC. In this method, a polynomial function is helpful to evaluate the system functions, and the performance is examined and then compared with the adaptive extended Kalman filter (AEKF). The AHF performed better in accuracy and computational cost than other methods.

3.4. Sigma Point Kalman Filter

This is another nonlinear technique for the calculation of states, and it achieves more precise outcomes than the extended Kalman filter. The sigma-point Kalman filter (SPKF) algorithm is subjected to a numerical approximation. The algorithm selects sets of sigma points that are identical to the mean and covariance values of the developed model. The SPKF has the advantage of having a similar calculation. Furthermore, without taking Jacobian matrices into account, the complexity of the EKF is reduced ^[39]^[40]. The SPKF can demonstrate more accuracy while using less memory and performing fewer computational calculations. However, the estimated SOC was compared with the SPKF, Luenberger observer, and EKF algorithms, and the drawbacks are heavy and complicated calculations ^[41]^[42].

4. Learning Algorithms

4.1. Neural Network (NN) Algorithm

An NN is a self-learning algorithm and also an intelligent tool. It uses trained data to estimate the state of the charge without knowing the initial data of the SOC. It consists of input, hidden, and output layers to form an NN structure^[43]. Building the NN structure takes discharge current, temperature, and voltage as inputs and the SOC as the output. The benefit of an NN is that it has a talent for being employed in nonlinear battery circumstances. The drawbacks are that training requires a large amount of data and a big memory to store the information ^[44]^[45].

4.2. Fuzzy Logic Algorithm

FL is the most influential algorithm for extending nonlinear, complex prototypes by using the training data. The employment of fuzzy logic includes rule-based inputs and outputs, a reasoning membership function, and defuzzification. However, estimating a nonlinear model is a powerful function. It needs an intricate calculation, dispensation unit, and large memory storage. Salkind et al. ^[46] applied FL for the estimation of SOC by using CC method data. This method uses three inputs at different frequencies, including impedances and SOC. It predicts the SOC with a max ±5% of error. The advanced ANFIS is most effective for estimating the SOC in Li-ion batteries; it was studied and applied in ^[47]^[48]^[49]^[50]^[51]^[52].

4.3. Genetic Algorithm (GA)

A genetic algorithm is mainly used for finding the optimum parameter. The primary function of a GA is to alter the constraint’s trendy active method to improve the efficacy of the arrangement. It has been applied in mathematics, physics, and engineering for identifying nonlinear optimal parameters. Zheng et al. ^[53] used a genetic algorithm to assess four LiFePO4 battery cells, which were allied on a sequence. In addition, the outcome of this method was under 1% of the estimated SOC error. Xu et al. ^[54] applied a genetic algorithm for finding the parameters. By using various driving cycles, the method was validated; the outcome of this method had better accuracy, with below 1% error.

4.4. Support Vector Machine Algorithm

The SVM algorithm practices regression algorithm and works on kernel function, which is intended for converting the nonlinear type in an inferior measurement into a linear variety in an extreme measurement. In ^[55], the SVM technique was used for SOC estimation. The independent variables current, temperature, and voltage were obtained to excerpt the model constraints even though the batteries were discharging/charging. This method was authenticated, and an approved extreme SOC precision of 0.97 estimated quantity was determined. The benefits of SVM are performing in high-dimension models and nonlinear forms. By using training data, the SOC is estimated quickly and accurately. The drawback of this method is that trial and process errors are needed and require a long time ^[56].

5. Nonlinear Observer (NLO)

5.1. Sliding Mode Observer (SMO)

SMO is an improved training controller for ensuring robustness and constancy of the system alongside model uncertainties as well as ecological disturbances. SMO is established by using the state equation in the next stage, which is decayed to the observer questions. In ^[57], a developed SMO was introduced to balance the nonlinear battery dynamic characteristics by using an RC circuit. This method can provide a controller for the conjunction period at the sophisticated discharge/charge value rate. The UDDS is situated to justify the method, and outcome details showed under 3% of the SOC error. In ^[58], the adaptive gain sliding mode observer (AGSMO) algorithm estimated the battery SOC on a combined equivalent circuit model. To extract the constraints, a battery pulse was used, and, by using the circuit model as well as terminal voltage, the state equations were developed. Experiments were performed to assess the recommended archetype, and outcomes proved that the model has an advantage in regulating the toughness derived when affecting all sound-on wrinkles.

5.2. Nonlinear Observer (NLO)

Several observers have been applied, including both a linear observer ^[59]^[60]^[61] as well as a nonlinear ^[62] observer, to estimate the SOC. In ^[63], the NLO-dependent SOC estimation was introduced via a first-order corresponding RC circuit. This model was performed by using a driving cycle as well as a discharge test, and the outcomes were improved compared to extended KF and SMO in standings of speed and precision as well as cost. They are still discovering an appropriate gain matrix to decrease the error.

6. Advanced SOC Estimation Techniques

6.1. Deep Learning Algorithm (DLA)

Deep learning (DL) algorithms have contributed to a better understanding of SOC estimation. Among the most notable are the long short-term memory (LSTM) network, deep neural networks (DNN), gated recurrent unit (GRU), and convolutional neural networks (CNN). The LSTM network ^[64] provides a strong SOC estimation performance because of its strong self-learning ability. The SOC of a battery is estimated using an LSTM network based on measured voltage, current, and temperature. Furthermore, DNN ^[65] exploits the battery’s dependent behaviors on ambient temperatures and encodes them into DNN weights, resulting in a competitive estimation performance over a wide range of temperatures. GRU ^[66] is used to estimate the battery SOC at different temperatures and to evaluate the performance of two common lithium-ion batteries. Unlike a traditional feedforward neural network, the RNN employs hidden nodes to store information about previous inputs, allowing the SOC estimation to incorporate this information. LSTM and GRU are RNN variants that extend the original RNN’s ability for long-term dependency. Another successful architecture in deep learning research is CNN. While the LSTM defines long-term dependency and is capable of handling time series data, the CNN employs convolutional behavior in a certain way to extract interconnections among input data. To model the complex battery dynamics, a combined CNN–LSTM network was proposed ^[67]. The CNN was specifically used to obtain advanced spatial features from the original data, while the LSTM was used to model relationships between the current SOC and past and present inputs. Both CNN and LSTM networks capture both spatial and temporal features of battery data.

6.2. Hybrid Methodologies

The mixing of two or more algorithms is known as a hybrid, which improves the accuracy and efficiency of the battery. It requires a large memory unit because of its complex mathematical computations. However, a hybrid methodology accomplishes consistent as well as operative outcomes and then, likewise, decreases the BMS price. In ^[68], the multi-state and extended Kalman filter methods were proposed, using the equivalent circuit model. The prototype is situated to move for a discrete state space that can provide supplementary data as opposed to linearized data by utilizing a Jacobian matrix. The simulation outcomes provided better accuracy, with a 2.7% average error. In ^[69], the CC, KF, and OCV methods were researched for SOC estimation. First, by using the OCV and CC methods, the SOC was estimated, which decreased the estimated error of CC. Then, the Kalman filter was utilized to enhance the precision value of the SOC.

In ^[70], a hybrid methodology was introduced; it included the CC and EKF methods for a time-changing dynamic estimation. The first open-circuit voltage method was applied for the SOC. The EKF was applied for the corrected SOC values, and this process was continued until the battery was fully discharged. The accuracy of the model was under 6.5%.

In ^[71], SOC was estimated based on AUKF utilizing RBF, and it was utilized to alter the particulars of the system. The AUKF stayed employed for evaluating the SOC. Then, united, both methods were equated by adaptive KF. The results of the AUKF were superior to the adaptive KF from the perspective of error. In ^[72], the H ∞ filter and discrete-time KF were applied to the nonlinear model of the Li-ion battery. The outcomes of this method were compared with adaptive Luenberger as well as SMO-based estimation models, and the accuracy of this method was improved, with <1% of error. In ^[73], the SOC of the lithium-ion cell was adaptively estimated using the multiple model adaptive estimation (MMAE) technique using a modified enhanced self-correcting (ESC) cell model. When compared to the EKF result, the SOC estimation converged more quickly. In ^[74], this designed an enhanced Kalman filter (KF)-based adaptive observer by approximating the electrochemical model. The estimator’s predictions were compared against the experimental data in simulations. The simulation outcomes were more precise and efficient than those of the KF. The accuracy of this method was improved, with <2% of error.

In ^[75], EKF paired with an adaptive neuro-fuzzy inference system (ANFIS) reduced error and improved accuracy over EKF alone. The root mean square error (RMSE) compared the EKF with the EKF-assisted ANFIS. In this way, the hybrid technology improved precision and accuracy while reducing expenses. In ^[76], for Li-ion batteries with uncertain noise circumstances, a new noise adaptive moving horizon estimating (NAMHE) approach was suggested. The simulation outcomes showed that the suggested technique reduced the SOC estimate error compared to the classic moving horizon estimating (MHE) method. The RMSE of the suggested technique and MHE were 0.7543% and 1.3026%, respectively. In ^[77], different OCV test methodologies impacted the correlation of the OCV and SOC; an effective OCV–SOC relationship may increase SOC online convergence speed and accuracy. The AEKF SOC estimate technique was more accurate and reliable than EKF during driving cycles, with a 0.5481% mean error of the proposed system. Hybrid methods give accurate outcomes and are cost-effective.

References

Yang, B.; Wang, J.; Cao, P.; Zhu, T.; Shu, H.; Chen, J.; Zhang, J.; Zhu, J. Classification, summarization and perspectives on state-of-charge estimation of lithium-ion batteries used in electric vehicles: A critical comprehensive survey. J. Energy Storage 2021, 39, 102572.
Snihir, I.; Rey, W.; Verbitskiy, E.; Belfadhel-Ayeb, A.; Notten, P.H. Battery open-circuit voltage estimation by a method of statistical analysis. J. Power Sources 2006, 159, 1484–1487.
Tingting, D.; Jun, L.; Fuquan, Z.; Yi, Y.; Qiqian, J. Analysis on the influence of measurement error on state of charge estimtion of LiFePO4 power Battery. In Proceedings of the 2011 International Conference on Materials for Renewable Energy & Environment 2011, Shanghai, China, 20–22 May 2011.
Lee, S.J.; Kim, J.H.; Lee, J.M.; Cho, B.H. The state and parameter estimation of an Li-ion battery using a new OCV-SOCconcept. In Proceedings of the 2007 IEEE Power Electronics Specialists Conference, Orlando, FL, USA, 17–21 June 2007.
Roscher, M.A.; Sauer, D.U. Dynamic electric behavior and open-circuit-voltage modeling of LiFePO4-based lithium ion secondary batteries. J. Power Sources 2011, 196, 331–336.
Zhang, Y.; Song, W.; Lin, S.; Feng, Z. A novel model of the initial state of charge estimation for LiFePO4 batteries. J. Power Sources 2014, 248, 1028–1033.
Leng, F.; Tan, C.M.; Yazami, R.; Le, M.D. A practical framework of electrical based online state-of-charge estimation of lithium ion batteries. J. Power Sources 2014, 255, 423–430.
Messing, M.; Shoa, T.; Ahmed, R.; Habibi, S. Battery SoC estimation from EIS using neural nets. In Proceedings of the 2020 IEEE Transportation Electrification Conference & Expo (ITEC), Chicago, IL, USA, 24–26 June 2020.
Li, M. Li-ion dynamics and state of charge estimation. Renew. Energy 2017, 100, 44–52.
Ran, L.; Junfeng, W.; Haiying, W.; Gechen, L. Prediction of state of charge of Lithium-ion rechargeable battery with electrochemical impedance spectroscopy theory. In Proceedings of the 2010 5th IEEE Conference on Industrial Electronics and Applications 2010, Taichung, Taiwan, 15–17 June 2010.
Meng, J.; Stroe, D.-I.; Ricco, M.; Luo, G.; Teodorescu, R. A Simplified Model-Based State-of-Charge Estimation Approach for Lithium-Ion Battery With Dynamic Linear Model. IEEE Trans. Ind. Electron. 2019, 66, 7717–7727.
Cho, S.; Jeong, H.; Han, C.; Jin, S.; Lim, J.H.; Oh, J. State-of-charge estimation for lithium-ion batteries under various opeating conditions using an equivalent circuit model. Comput. Chem. Eng. 2012, 41, 1–9.
Rahman, A.; Anwar, S.; Izadian, A. Electrochemical model parameter identification of a lithium-ion battery using particle swarm optimization method. J. Power Sources 2016, 307, 86–97.
Stetzel, K.D.; Aldrich, L.L.; Trimboli, M.; Plett, G.L. Electrochemical state and internal variables estimation using a reduced-order physics-based model of a lithium-ion cell and an extended Kalman filter. J. Power Sources 2015, 278, 490–505.
Di Domenico, D.; Fiengo, G.; Stefanopoulou, A. Lithium-ion battery state of charge estimation with a Kalman Filter based on a electrochemical model. In Proceedings of the 2008 IEEE International Conference on Control Applications, San Antonio, TX, USA, 3–5 September 2008.
Bruen, T.; Marco, J. Modelling and experimental evaluation of parallel connected lithium ion cells for an electric vehicle battery system. J. Power Sources 2016, 310, 91–101.
Lai, X.; Gao, W.; Zheng, Y.; Ouyang, M.; Li, J.; Han, X.; Zhou, L. A comparative study of global optimization methods for parameter identification of different equivalent circuit models for Li-ion batteries. Electrochim. Acta 2019, 295, 1057–1066.
Xu, L.; Wang, J.; Chen, Q. Kalman filtering state of charge estimation for battery management system based on a stochastic fuzzy neural network battery model. Energy Convers. Manag. 2012, 53, 33–39.
Ting, T.O.; Man, K.L.; Lim, E.; Leach, M. Tuning of Kalman Filter Parameters via Genetic Algorithm for State-of-Charge Estimation in Battery Management System. Sci. World J. 2014, 2014, 176052.
Urbain, M.; Rael, S.; Davat, B.; Desprez, P. State Estimation of a Lithium-Ion Battery Through Kalman Filter. In Proceedings of the 2007 IEEE Power Electronics Specialists Conference 2007, Orlando, FL, USA, 17–21 June 2007.
Yatsui, M.W.; Bai, H. Kalman filter-based state-of-charge estimation for lithium-ion batteries in hybrid electric vehicles using pulse charging. In Proceedings of the 2011 IEEE Vehicle Power and Propulsion Conference, Chicago, IL, USA, 6–9 September 2011.
Jokic, I.; Zecevic, Z.; Krstajic, B. State-of-charge estimation of lithium-ion batteries using extended Kalman filter and unscented Kalman filter. In Proceedings of the 2018 23rd International Scientific-Professional Conference on Information Technology (IT), Žabljak, Montenegro, 19–24 February 2018.
Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 3. State and parameter estimation. J. Power Sources 2004, 134, 277–292.
Ben Sassi, H.; Errahimi, F.; Es-Sbai, N. State of charge estimation by multi-innovation unscented Kalman filter for vehicular applications. J. Energy Storage 2020, 32, 101978.
Chen, Z.; Fu, Y.; Mi, C. State of Charge Estimation of Lithium-Ion Batteries in Electric Drive Vehicles Using Extended Kalman Filtering. IEEE Trans. Veh. Technol. 2013, 62, 1020–1030.
Fang, Y.; Zhang, Q.; Zhang, H.; Xu, W.; Wang, L.; Shen, X.; Yun, F.; Cui, Y.; Wang, L.; Zhang, X. State-of-charge estimation technique for lithium-ion batteries by means of second-order extended Kalman filter and equivalent circuit model: Great temperature robustness state-of-charge estimation. IET Power Electron. 2021, 14, 1515–1528.
Liu, X.; Li, K.; Wu, J.; He, Y.; Liu, X. An extended Kalman filter based data-driven method for state of charge estimation of Li-ion batteries. J. Energy Storage 2021, 40, 102655.
Nian, P.; Shuzhi, Z.; Xiongwen, Z. Co-estimation for capacity and state of charge for lithium-ion batteries using improved adaptive extended Kalman filter. J. Energy Storage 2021, 40, 102559.
Xiong, R.; He, H.; Sun, F.; Zhao, K. Evaluation on State of Charge Estimation of Batteries With Adaptive Extended Kalman Filter by Experiment Approach. IEEE Trans. Veh. Technol. 2013, 62, 108–117.
Wang, S.; Fernandez, C.; Shang, L.; Li, Z.; Li, J. Online state of charge estimation for the aerial lithium-ion battery packs based on the improved extended Kalman filter method. J. Energy Storage 2017, 9, 69–83.
Espedal, I.B.; Jinasena, A.; Burheim, O.S.; Lamb, J.J. Current Trends for State-of-Charge (SoC) Estimation in Lithium-Ion Battery Electric Vehicles. Energies 2021, 14, 3284.
Wassiliadis, N.; Adermann, J.; Frericks, A.; Pak, M.; Reiter, C.; Lohmann, B.; Lienkamp, M. Revisiting the dual extended Kalman filter for battery state-of-charge and state-of-health estimation: A use-case life cycle analysis. J. Energy Storage 2018, 19, 73–87.
Sangwan, V.; Kumar, R.; Rathore, A.K. State-of-Charge estimation of Li-ion battery at different temperatures using particle filter. J. Eng. 2019, 2019, 5320–5324.
Gao, M.; Liu, Y.; He, Z. Battery state of charge online estimation based on particle filter. In Proceedings of the 2011 4th International Congress on Image and Signal Processing, Shanghai, China, 15–17 October 2011.
Schwunk, S.; Armbruster, N.; Straub, S.; Kehl, J.; Vetter, M. Particle filter for state of charge and state of health estimation for lithium–iron phosphate batteries. J. Power Sources 2013, 239, 705–710.
He, Y.; Liu, X.; Zhang, C.; Chen, Z. A new model for State-of-Charge (SOC) estimation for high-power Li-ion batteries. Appl. Energy 2013, 101, 808–814.
Zhang, Y.; Zhang, C.; Zhang, X. State-of-charge estimation of the lithium-ion battery system with time-varying parameter for hybrid electric vehicles. IET Control Theory Appl. 2014, 8, 160–167.
Charkhgard, M.; Zarif, M.H. Design of adaptive H ∞ filter for implementing on state-of-charge estimation based on battery state-of-charge-varying modelling. IET Power Electron. 2015, 8, 1825–1833.
Zhang, J. Battery state-of-charge estimation based on sigma point Kalman filter. In Proceedings of the 2011 2nd International Conference on Artificial Intelligence, Management Science and Electronic Commerce (AIMSEC), Zhengzhou, China, 8–10 August 2011.
Plett, G.L. Sigma-point Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 2: Simultaneous state and parameter estimation. J. Power Sources 2006, 161, 1369–1384.
He, Z.; Liu, Y.; Gao, M.; Wang, C. A joint model and SOC estimation method for lithium battery based on the sigma point KF. In Proceedings of the 2012 IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, USA, 17–20 June 2012.
He, Z.; Gao, M.; Xu, J.; Liu, Y. Battery Model Parameters Estimation with the Sigma Point Kalman Filter. In Proceedings of the 2009 International Conference on Artificial Intelligence and Computational Intelligence, Shanghai, China, 7–8 November 2009.
He, W.; Williard, N.; Chen, C.; Pecht, M. State of charge estimation for Li-ion batteries using neural network modeling and unscented Kalman filter-based error cancellation. Int. J. Electr. Power Energy Syst. 2014, 62, 783–791.
Chen, Z.; Qiu, S.; Masrur, M.; Murphey, Y.L. Battery state of charge estimation based on a combined model of Extended Kalman Filter and neural networks. In Proceedings of the 2011 International Joint Conference on Neural Networks, San Jose, CA, USA, 31 July–5 August 2011.
Rui-Hao, L.; Yu-Kun, S.; Xiao-Fu, J. Battery state of charge estimation for electric vehicle based on neural network. In Proceedings of the 2011 IEEE 3rd International Conference on Communication Software and Networks, Xi’an, China, 27–29 May 2011.
Salkind, A.J.; Fennie, C.; Singh, P.; Atwater, T.; Reisner, D.E. Determination of state-of charge and state-of-health of batteries by fuzzy logic methodology. J. Power Sources 1999, 80, 293–300.
Jamlouie, M.H.A. Accuracy improvement of SOC estimation in lithium-ion batteries by ANFIS vs. ANN modeling of nonlinear cell characteristics. J. Energy Storage 2021, 6, 95–104.
Singh, P.; Vinjamuri, R.; Wang, X.; Reisner, D. Design and implementation of a fuzzy logic-based state-of-charge meter for Li-ion batteries used in portable defibrillators. J. Power Sources 2006, 162, 829–836.
Malkhandi, S. Fuzzy logic-based learning system and estimation of state-of-charge of lead-acid battery. Eng. Appl. Artif. Intell. 2006, 19, 479–485.
Li, I.-H.; Wang, W.-Y.; Su, S.-F.; Lee, Y.-S. A Merged Fuzzy Neural Network and Its Applications in Battery State-of-Charge Estimation. IEEE Trans. Energy Convers. 2007, 22, 697–708.
Cai, C.H.; Du, D.; Liu, Z.Y. Battery state-of-charge (SOC) estimation using adaptive neuro-fuzzy inference system (ANFIS). In Proceedings of the 12th IEEE International Conference on Fuzzy Systems, St. Louis, MO, USA, 25–28 May 2003.
Shen, W.; Chan, C.; Lo, E.; Chau, K.T. Adaptive neuro-fuzzy modeling of battery residual capacity for electric vehicles. IEEE Trans. Ind. Electron. 2002, 49, 677–684.
Zheng, Y.; Lu, L.; Han, X.; Li, J.; Ouyang, M. LiFePO4 battery pack capacity estimation for electric vehicles based on charging cell voltage curve transformation. J. Power Sources 2013, 226, 33–41.
Xu, J.; Cao, B.; Chen, Z.; Zou, Z. An online state of charge estimation method with reduced prior battery testing information. Int. J. Electr. Power Energy Syst. 2014, 63, 178–184.
Antón, J.C.Á.; Nieto, P.J.G.; de Cos Juez, F.J.; Lasheras, F.S.; Vega, M.G.; Gutiérrez, M.N.R. Battery state-of-charge estimator using the SVM technique. Appl. Math. Model. 2013, 37, 6244–6253.
Wu, X.; Mi, L.; Tan, W.; Qin, J.L.; Na Zhao, M. State of Charge (SOC) Estimation of Ni-MH Battery Based on Least Square Support Vector Machines. Adv. Mater. Res. 2011, 211–212, 1204–1209.
Kim, I.-S. Nonlinear State of Charge Estimator for Hybrid Electric Vehicle Battery. IEEE Trans. Power Electron. 2008, 23, 2027–2034.
Chen, X.; Shen, W.; Cao, Z.; Kapoor, A.; Hijazin, I. Adaptive gain sliding mode observer for state of charge estimation based on combined battery equivalent circuit model in electric vehicles. Aust. J. Electr. Electron. Eng. 2013, 9, 601–606.
Boizot, N.; Busvelle, E.; Gauthier, J.-P. An adaptive high-gain observer for nonlinear systems. Automatica 2010, 46, 1483–1488.
Xu, J.; Mi, C.; Cao, B.; Deng, J.; Chen, Z.; Li, S. The State of Charge Estimation of Lithium-Ion Batteries Based on a Proportional-Integral Observer. IEEE Trans. Veh. Technol. 2014, 63, 1614–1621.
Xu, F.; Wang, Y.; Luo, X. Soft Sensor for Inputs and Parameters Using Nonlinear Singular State Observer in Chemical Processes. Chin. J. Chem. Eng. 2013, 21, 1038–1047.
Kim, I.-S. The novel state of charge estimation method for lithium battery using sliding mode observer. J. Power Sources 2006, 163, 584–590.
Xia, B.; Chen, C.; Tian, Y.; Sun, W.; Xu, Z.; Zheng, W. A novel method for state of charge estimation of lithium-ion batteries using a nonlinear observer. J. Power Sources 2014, 270, 359–366.
Chemali, E.; Kollmeyer, P.J.; Preindl, M.; Ahmed, R.; Emadi, A.; Kollmeyer, P. Long Short-Term Memory Networks for Accurate State-of-Charge Estimation of Li-ion Batteries. IEEE Trans. Ind. Electron. 2018, 65, 6730–6739.
How, D.N.; Hannan, M.; Lipu, M.H.; Sahari, K.S.; Ker, P.J.; Muttaqi, K.M. State-of-charge estimation of li-ion battery in electric vehicles: A deep neural network approach. IEEE Trans. Ind. Appl. 2020, 56, 5565–5574.
Yang, F.; Li, W.; Li, C.; Miao, Q. State-of-charge estimation of lithium-ion batteries based on gated recurrent neural network. Energy 2019, 175, 66–75.
Song, X.; Yang, F.; Wang, D.; Tsui, K.-L. Combined CNN-LSTM Network for State-of-Charge Estimation of Lithium-Ion Batteries. IEEE Access 2019, 7, 88894–88902.
Li, Y.; Wang, L.; Liao, C.; Wang, L.; Xu, D.; Yong, L.; Lifang, W.; Chenglin, L.; Liye, W.; Dongping, X. State-of-Charge Estimation of Lithium-Ion Battery Using Multi-State Estimate Technic for Electric Vehicle Applications. In Proceedings of the 2013 IEEE Vehicle Power and Propulsion Conference (VPPC), Beijing, China, 15–18 October 2013.
Alfi, A.; Charkhgard, M.; Zarif, M.H. Hybrid state of charge estimation for lithium-ion batteries: Design and implementation. IET Power Electron. 2014, 7, 2758–2764.
Xu, J.; Gao, M.; He, Z.; Han, Q.; Wang, X. State of Charge Estimation Online Based on EKF-Ah Method for Lithium-Ion Power Battery. In Proceedings of the 2009 2nd International Congress on Image and Signal Processing, Tianjin, China, 17–19 October 2009.
Liu, Z.; Wang, Y.; Du, J.; Chen, C. RBF network-aided adaptive unscented kalman filter for lithium-ion battery SOC estimation in electric vehicles. In Proceedings of the 2012 7th IEEE Conference on Industrial Electronics and Applications (ICIEA), Singapore, 18–20 July 2012.
Unterrieder, C.; Priewasser, R.; Marsili, S.; Huemer, M. Battery state estimation using mixed Kalman/hinfinity, adaptive luenberger and sliding mode observer. In Proceedings of the 2013 IEEE Vehicle Power and Propulsion Conference (VPPC), Beijing, China, 15–18 October 2013.
Su, J.; Schneider, S.; Yaz, E.; Josse, F. Online State of Charge Estimation of Lithium-ion Battery Cells: A Multiple Model Adaptive Estimation Approach. In Proceedings of the 2021 American Control Conference (ACC), New Orleans, LA, USA, 25–28 May 2021.
Afshar, S.; Morris, K.; Khajepour, A. State-of-Charge Estimation Using an EKF-Based Adaptive Observer. IEEE Trans. Control Syst. Technol. 2019, 27, 1907–1923.
Shabarish, P.R.; Aditya, D.V.S.S.; Pavan, V.V.S.S.P.; Manitha, P.V. SOC estimation of battery in hybrid vehicle using adaptive neuro-fuzzy technique. In Proceedings of the 2020 International Conference on Smart Electronics and Communication (ICOSEC), Trichy, India, 10–12 September 2020.
Zhang, Z.; Xue, B.; Fan, J. Noise Adaptive Moving Horizon Estimation for State-of-Charge Estimation of Li-Ion Battery. IEEE Access 2021, 9, 5250–5259.
Li, Y.; Guo, H.; Qi, F.; Guo, Z.; Li, M. Comparative Study of the Influence of Open Circuit Voltage Tests on State of Charge Online Estimation for Lithium-Ion Batteries. IEEE Access 2020, 8, 17535–17547.

© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.

Upload a video for this entry

Information

Subjects: Engineering, Electrical & Electronic

Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :

Dhanamjayulu Chittathuru

T GIRIJA PRASANNA

View Times: 2.6K

Update Date: 27 Jun 2022

Table of Contents

Video Upload Options

Confirm