You're using an outdated browser. Please upgrade to a modern browser for the best experience.

Submitted Successfully!
Thank you for your contribution! You can also upload a video entry or images related to this topic.
For video creation, please contact our Academic Video Service.
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Alexey V. Shkirin | -- | 4200 | 2022-06-17 14:00:46 | | | |
| 2 | Peter Tang | Meta information modification | 4200 | 2022-06-20 04:03:27 | | |
Video Upload Options
We provide professional Academic Video Service to translate complex research into visually appealing presentations. Would you like to try it?
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Shkirin, A.; Ignatenko, D.; Lobachevsky, J.; Gudkov, S. Mueller Matrix Polarimetry in Biological and Agricultural Diagnostics. Encyclopedia. Available online: https://encyclopedia.pub/entry/24165 (accessed on 22 December 2025).
Shkirin A, Ignatenko D, Lobachevsky J, Gudkov S. Mueller Matrix Polarimetry in Biological and Agricultural Diagnostics. Encyclopedia. Available at: https://encyclopedia.pub/entry/24165. Accessed December 22, 2025.
Shkirin, Alexey, Dmitry Ignatenko, Jacob Lobachevsky, Sergey Gudkov. "Mueller Matrix Polarimetry in Biological and Agricultural Diagnostics" Encyclopedia, https://encyclopedia.pub/entry/24165 (accessed December 22, 2025).
Shkirin, A., Ignatenko, D., Lobachevsky, J., & Gudkov, S. (2022, June 17). Mueller Matrix Polarimetry in Biological and Agricultural Diagnostics. In Encyclopedia. https://encyclopedia.pub/entry/24165
Shkirin, Alexey, et al. "Mueller Matrix Polarimetry in Biological and Agricultural Diagnostics." Encyclopedia. Web. 17 June, 2022.
Copy Citation
The Mueller matrix (4 × 4) most fully describes the interaction of an arbitrary object with fully or partially polarized electromagnetic radiation; therefore, the existing polarimetric methods can be generalized by the Mueller matrix formalism, and that generalization is termed Mueller matrix polarimetry (MMP). Mueller matrix measurements, being integrated into standard schemes of conventional optical methods, such as scatterometry, optical coherence tomography, fluorimetry, spectrophotometry and reflectometry, can significantly expand their capabilities in the characterization of biological systems and bioorganic materials.
Mueller matrix polarimetry
scatterometry
spectropolarimetry
OCT
fluorimetry
ellipsometry
biology
agriculture
1. Introduction
For the last several decades, non-destructive methods for studying biological systems and bioorganic materials have been increasingly used to analyze the composition of drugs, the structure of biological tissues, the microbiology of food products, the concentration of dispersions, the content of complex organic substances in water and soil and so on. However, the physical characteristics of many biological and food samples are inherently difficult to measure using traditional contact procedures due to the fact that samples can be sticky, very viscous or contain particles of different sizes and shapes. Consequently, there exists a need to develop reliable, multi-functional, automated sensors which are capable of rapidly and continuously monitoring the state of the system under test.
In order to carry out non-destructive diagnostics, various optical methods based on the detection of transmitted or scattered light are used [1][2][3][4][5]. However, conventional optical instruments usually measure only the light intensity without taking into account changes in the polarization state of the light. Techniques that also detect polarization changes can provide additional information about the investigated medium and improve measurement accuracy. The Mueller matrix (4 × 4) most fully describes the interaction of an arbitrary object with fully or partially polarized electromagnetic radiation; therefore, the existing polarimetric methods can be generalized by the Mueller matrix formalism, and that generalization is termed Mueller matrix polarimetry (MMP) [6][7][8][9][10][11][12][13]. In the case of a scattering medium, a light scattering matrix (LSM), defined in the sense of the Mueller matrix (MM), is directly influenced by the physical characteristics of the scatterers and is very sensitive to the optical properties, shape and size distribution of scattering particles [3][4][5][14][15][16][17][18]. Thus, it is possible to obtain these characteristics by solving the inverse scattering problem. For example, when their size exceeds the wavelength of light, it becomes possible to determine whether they are separate monolithic particles or aggregates of particles smaller than the wavelength. Elucidation of the features of the angular and spectral dependences of matrix elements for various kinds of dispersed system, taking into account the aggregation of particles in the dispersed phase, makes it possible to develop a method for retrieving the parameters of the microphysical structure of the investigated dispersed system from the measured values of the Mueller matrix elements. More specifically, the number, size of particles and their state of aggregation can be determined.
MMP has recently begun to find wide application in many fields of science and technology, including physical chemistry, geophysics, biomedicine and pharmacology, technological control, environmental monitoring and agriculture. Non-destructive diagnostic methods based on the measurement of the Mueller matrix elements are widely used to obtain information on the properties of colloidal solutions and suspensions, rough surfaces of materials, nanoparticle coatings and composite materials, which can be multilayer systems of discrete scattering particles, as well as to study microbiological systems and biological tissues. These methods are relatively inexpensive to implement and can be easily automated, allowing quick results in laboratory research, industry or the field. So, technologies based on MMP are already being developed for non-destructive analysis in biology, biomedicine and agriculture.
2. Principles of Mueller Matrix Analysis
The Mueller matrix M describes the transformation of the Stokes vector S→, which represents the state of light polarization due to the interaction of light with an object. The components of the Stokes vector that are called the Stokes parameters can be expressed in terms of the intensities of the basic polarized components of the light wave as follows:

where I, Q, U and V are the Stokes parameters, Ix, Iy and I±45° are the intensities of linearly polarized components oriented along the corresponding directions (x, y, ±45°) and IR,L are the intensities of right and left circular polarized components.

In the case of dispersed media, the light scattering matrix (LSM) defined as the Mueller matrix (MM) contains the most complete information on particles scattering light that is available for static scattering. The LSM elements, being functions of the scattering angle, also depend on the wavelength of the probe radiation, optical properties and size distribution of the dispersed entities [3][4][5][14][15][16][17][18][21]. In the particular case of spherical particles, it has a block-diagonal structure:

where M11=M22, M12=M21, M34=−M43 and M33=M44. The physical meaning of the element M11(θ) is the scattering indicatrix, that is, the angular distribution of the scattered light intensity (θ is the scattering angle).
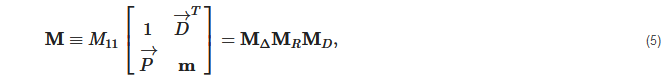


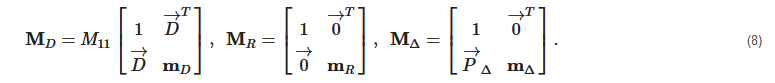

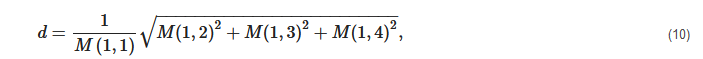

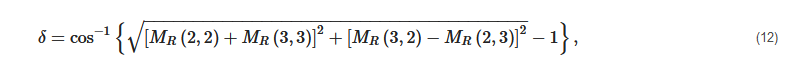
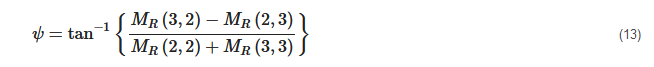
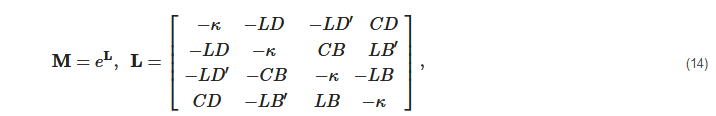



For example, the M34 element normalized to M11 or M33 is sensitive to changes in the morphological properties of bacterial colonies during growth [16][22], while the normalized M14 element is sensitive to changes in the structure of chiral polymers, such as DNA [16][23][24].
To better understand how the angular variations are related to the properties of the medium, numerical modeling of the angular-resolved radiation transfer problem was considered in [25]. It was found that light is anisotropically reflected from all media encountered in practice, and that the angular changes depend on the absorption and transmission of the medium, as well as on the angular distribution of the incident light.
Particle diagnostics using the MM are carried out, in fact, by the mathematical processing of its elements measured for scattering, absorption and emission of light in accordance with the selected structural model of the investigated medium or sample in order to extract the values of its microphysical parameters [4]. The simplest structural model is a collection of spherical particles. However, particles can be both solid elements and clusters of such particles, as well as have different shapes and sizes, to which the MM is also sensitive [5]. Various mathematical approaches are used to solve the inverse problem from the MM. Most often, it is decompositions of directly measured MM [11][13][20][26], in particular, using group theory [27] or stochastic simulations by the Monte Carlo method [28][29][30][31]. Monte Carlo simulations of MMs for multiple scattering media are very important in interpreting MMs measured for turbid media such as biological tissues [32][33].
It is worth dwelling on some details of the MM polar decomposition method [20][26]. Lu and Chipman proposed a procedure for decomposing a MM into a successive product of three basis matrices [34].
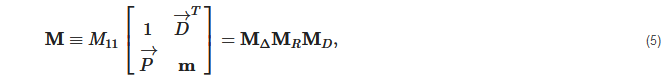
The original matrix M is partitioned into the polarizance vector P→, the diattenuation vector D→:

and 3 × 3 submatrix m:

The matrices MΔ, MR and MD have the following form:
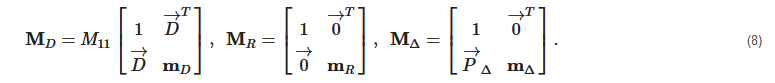
A set of polarimetric parameters that are related to the intrinsic properties of the tissue can be derived from this representation of the MM. These parameters are considered to be as follows [26]:
Depolarization:

Diattenuation:
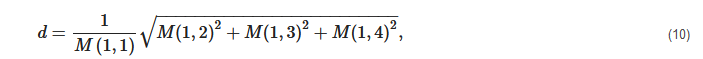
Total retardance:

Linear retardance:
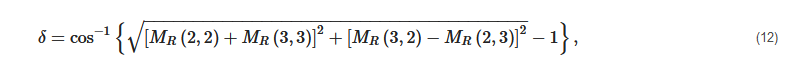
Optical rotation:
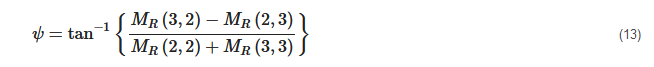
Such a representation of the MM and the parameters thus defined are especially informative in tissue diagnostics.
For light transmitted through a homogeneous, anisotropic material, the polarization effects are described by a set of eight parameters with a clear physical interpretation: circular dichroism (CD), circular birefringence (CB), horizontal linear dichroism (LD), 45° linear dichroism (LD′), horizontal linear birefringence (LB), 45° linear birefringence (LB′), isotropic retardation (η) and isotropic amplitude absorption (κ). In terms of these parameters, the MM of a non-depolarizing sample can be written as a matrix exponent [8]:
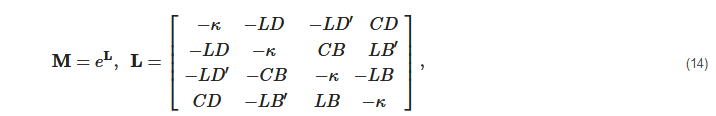
If an anisotropic material is only transversely homogeneous, then the differential expansion of the MM can be applied to analyze the evolution of its polarization properties along the direction of light propagation [20].
In the context of the diagnostics of organic substances, the results of comparing three approaches to determine the parameters of optical chirality [12]—direct evaluation from the MM elements, differential decomposition of the MM and electromagnetic modeling using Tellegen’s constitutive relations—may be of interest.
The operation principle of the polarimetric devices measuring the MM (MM polarimeters) can be illustrated by a general block diagram (Figure 1).

Figure 1. General block diagram of MM polarimeters: light source (LS), polarization state generator PSG, sample (S), polarization state analyzer (PSA), photodetector (PD).
In general, an MM polarimeter consists of a light source (LS), a polarization state generator (PSG), a test sample cuvette (S), a polarization state analyzer (PSA) and a photodetector (PD). Light sources can vary depending on the purpose of the polarimetric instrument and the accuracy of the measurements, from broadband lamps and super luminescent diodes [12][35][36][37] to lasers [14][21], including tunable lasers [38]. A polarization state generator (PSG) is a transmissive optical system that allows the generation of any arbitrary polarization state (generally elliptical) and is used to convert the polarization of source radiation which is not initially polarized or has constant polarization into a set of polarized light states that is required for measuring the Mueller matrix of an arbitrary object. They can have different designs; the most common PSG in polarimetric instruments consists of a combination of phase modulators, phase plates and a linear polarizer [14][15][36][37][38]. Note that PSGs based on liquid crystals are very promising [36][39], since they are compact and have no moving parts. On the basis of full Poincaré beams, which represent all possible completely polarized states of polarization in their cross-section and can be generated by focusing a laser beam on the front face of a uniaxial crystal, it is possible to implement a parallel-type PSG [40].
After the PSG, the polarization state of the radiation is changed (time-modulated). Two ways are possible here:
- Polarization is modulated continuously or pulse-modulated (periodically, as a rule);
- Polarization sequentially passes a fixed, discrete set of time-constant states.
In the first case, the Stokes vector of radiation, after passing through the PSG to be incident on the object, has the form:

where yi(t) are known time functions determined by the modulation method. The Stokes vector at the output of the object is expressed as follows:

where M is the MM of the object.

If the functions yi(t) are linearly independent, then the matrix elements Mik can be obtained as the corresponding coefficients of the expansions of the measured Stokes vector components S∗i in these functions.
In the second case, it is necessary to set at least four discrete polarization states of the input radiation, which are described by linearly independent Stokes vectors S→(j) (j=1…4). Having measured the four corresponding output Stokes vectors S→*(j) (j=1…4), the researhers obtain a system of 16 linear algebraic equations:

The solution of this system gives the values of all 16 elements of the Muller matrix of the object.
Similar to a PSG, a PSA is also a combination of phase optical elements (phase modulators, phase plates) and a linear polarizer, which serves to measure the components of the Stokes vector of radiation coming out of an object. For instance, a PSA using a certain set of relative azimuthal orientations of a linear polarizer together with a quarter-wave plate enables complete Stokes vector measurements. Actually, this PSA successively implements particular cases of a linear polarizer oriented at 0°, 90° and ±45° and a circular polarizer.
For spectroscopic measurements of the MM, it is attractive to use polarimeters with four photoelastic modulators, two each in the PSG and PSA, since modulators of this type are easily adjusted to different wavelengths [41]. Having no moving parts, they perform relatively fast MM measurements, which, additionally, can be made with spatial resolution.
Error analysis of a MM polarimeter carried out in [42] provided a basis for the calibration procedure in order to correct angular misalignments and compensate for retardance errors and, thus, obtain accurate values of the Mueller matrix elements.
It is worth noting that the sample type—biological tissue, solid surface or aqueous suspension, etc.—determines the scheme for receiving light after interaction with the sample (S). Radiation scattered or reflected from the sample can be detected either directly or using a collecting and directing optical system. For example, weakly scattering samples can be placed in immersion cuvettes. In many cases, it is convenient to use standard spectroscopic plane-parallel cells, which require operation together with lenses. Lenses can be moved to focus light from different areas of the sample. The photodetector (PD) is used in conjunction with a signal acquisition system to interface with a computer to determine the MM based on digital signal processing algorithms.
The block diagram (Figure 1) shows that the measurement of the Mueller matrix of an object requires the introduction of polarimetric blocks PSG and PSA into the optical system before and after the object. The next section shows general schemes of the most common optical instruments (scatterometers, OCT systems, transmission or fluorescence spectrometers, ellipsometers) used to study various types of bioorganic systems, which, when supplemented with polarimetric elements, enable the measurement of the complete Mueller matrix.
3. Basic Schemes for Using Mueller Matrix Polarimetry in Optical Diagnostics of Biological and Bioorganic Systems
Optical methods of non-destructive diagnostics can be divided into four groups. The first group includes methods based on measuring the angular distribution of light scattered by a sample (scatterometers) and the polarization features of the scattered light. The second group is imaging systems for densely structured objects, such as biological tissues, in particular those which detect backscattered light from a narrow layer in depth through low coherence interferometry; this is called optical coherence tomography (OCT). The third group includes spectrophotometers that measure the dependence of the transmission/absorption of light by a sample of the light wavelength, that is, spectral methods. The fourth group is devoted to fluorescence spectrometers separately. To these techniques, the general principle of modifying the optical design by surrounding the studied sample with polarimetric blocks (PSG and PSA) can be applied in order to expand measurement capabilities from light intensity alone to the complete Mueller matrix.
4. Applications of MMP to Biology and Agriculture
The considered examples of MMP implementation show that MMP is a powerful tool for non-invasive diagnostics of bioorganic systems, especially in combination with other optical techniques, significantly expanding their capabilities. The above research of MMP installations allows us to systematize optical methods supplemented by MM measurements into groups depending on:
- Geometry of the sample—volumetric (MM scatterometry, MM spectrophotometry, MM fluorometry) and surface (MM-OCT and MM ellipsometry);
- Properties of incoming radiation—spectral (spectrophotometry and spectroscopic MM scatterometry, MM fluorometry and MM ellipsometry) and non-spectral (MM-OCT and single-wavelength MM scatterometry, MM fluorometry and MM ellipsometry);
- Received information—visual (MM-OCT and other methods of polarization-sensitive imaging) and structural (all methods that measure the MM with subsequent retrieval of the microphysical parameters of the sample using inverse analysis);
- Operating conditions—stationary and mobile.
4.1. Studying the Structure of Organic Materials
MMP can be a useful tool for studying various materials in order to assess the quality of products made from them and, subsequently, detect defects. An experimental procedure using MMP, which enables studying foams, was described in [43]. The use of MM spectroscopic ellipsometry to study the anisotropy of materials, in particular, polyethylene terephthalate (PET) was proposed in [44]; this method proved to be successful in obtaining additional information about the anisotropy of materials. MMP was used to study films of chiral nanocrystalline cellulose [45] and to measure the anisotropy and orientation of liquid crystals [46]. Strain-induced birefringence shows linear relationships with both strain and orientation of chain segments. MM scatterometry was used to compare the polarization properties of white fabric and white wood [47]. Linear and circular birefringence, as well as circular dichroism in chiral nanocellulose films obtained by self-assembly of cellulose nanocrystals, were estimated using MMP [48]. Optical chirality parameters were determined from MM measured for organic materials such as sugar solutions and liquid crystals [12]. The MM-based measurement of the intensity difference between right and left circular polarizations in light scattered from an optically active medium is sensitive to the molecular conformation of complex biopolymers [23].
MMP can be used to quantify the anisotropy of plant fibers by the MM differential decomposition [49]. Measuring the topology of polymer fiber scaffolds by MMP is of considerable interest for tissue engineering [50]. It has been shown that the MM responds to the orientation of the fibers and their mechanical properties, which confirms the accuracy of the MMP method is sufficient for evaluating fiber structures.
Tomographic Mueller scatterometry (TMS) can visualize the topology of structures down to tens of nanometers in size, which is promising for non-destructive testing in nano-manufacturing [51].
IR laser spectroellipsometry [38] and polarimetric FTIR spectroscopy [52][53][54][55] aiming to measure the Mueller matrix of liquid and solid organic materials would be suitable, in particular, for complex analysis of fodders to determine fat, protein, fiber, ash or grain gluten content.
MMP is very important in studying protein systems. For example, the fractal structure of protein aggregates can be determined from the light scattering matrix [56]. Additionally, fluorescence polarization measurements [57], especially in the form of the Mueller matrix [58], provide information on molecular orientation and mobility and the processes that modulate them, including receptor–ligand interactions, protein–protein and protein–nucleic acid interactions, proteolysis and fluidity membranes [59].
4.2. Microbiological Research
MMP is relevant for the detection of viruses and microorganisms. For example, MMP was used to analyze blood for the presence of the dengue virus [60]. It was found that blood samples with dengue fever virus have a higher depolarization factor than normal samples, which, hypothetically, could allow the detection of this virus in the early stages of infection. Changes in the growth of rod-shaped bacteria were studied using polarimetric scatterometry [22]. The block-diagonal elements of MM are sensitive to the size and shape of microbiological entities, as shown in the example of microalgae in [61]. Quantitative parameters for distinguishing between different bacterial colonies can be acquired from MM images using the MM polar decomposition method, frequency distribution histograms and the central moment analysis method [62]. Water-polarized reflectance was investigated to retrieve the properties of oceanic constituents (suspended organic matter and phytoplankton), primarily their concentration and biomass [63].
4.3. Biological Tissues
The concepts and applications of tissue MMP were concisely reviewed in [26]. Inverse analysis of MMs based on scattering theory and MM polar decomposition was considered. Several medium-specific polarimetric parameters that are practical for recognizing tissue structures and their changes can be derived from the polar decomposition of MM: diattenuation, depolarization (linear, circular and total), linear retardance (and its orientation) and optical rotation.
MMP increases the quality of visualization of biological tissues and, in particular, makes it possible to distinguish between cancerous and healthy tissues, while being, at the same time, a cheaper method for analysis of tissues before and after surgery [64][65].
Microscopic imaging based on MM-derived parameters related to depolarization and retardance proved to be effective in assessing the polarization properties and structural features of biological tissues and were helpful for diagnosing pathological tissue samples [66]. In particular, measuring the retardance and depolarization of thin biopsies by MMP can be used to quantify human liver fibrosis [67]. MMP was tested as a non-invasive method for the characterization of various dermatological diseases [68][69]. The depolarization and retardance were shown to be important polarization metrics, indicating changes in the fibrous structure of skin tissues. OCT integrated with MMP can record tissue anisotropies and is capable of measuring the polarization contrast of any biological sample, in particular, soft tissue samples [70]. MM-based polarization imaging was used for quantitative digital screening of polycrystalline structures of biological tissues in vitro [71]. It was shown that the spatial distributions of the phase of light and optical anisotropy of scattering, which are inherent in myocardial fibrillar networks at different stages of necrosis, can be effectively used as a quantitative marker of the stages of myosin fibril degradation. The use of MM calculus facilitates the calibration of fiber-optic PS-OCT to quantitatively measure the birefringence and optical axis orientation of tissues [72].
Monte Carlo simulations showed the possibility of determining the glucose concentration in turbid media using MMs [30]. Similar studies showed that linear polarization and total intensity are more sensitive to increased glucose concentration in backscatter than in forward scatter in highly turbid environments, indicating that backscatter geometry may be preferable for potential glucose detection in biomedical diagnostics. At the same time, comparative measurements with optically inactive glycerol showed that the refractive index matching effect, rather than the chiral nature of the solute, dominates the observed optical rotation caused by glucose in a highly turbid medium [73]. By multi-region segmentation of polarized light images, a radiofrequency-ablated lesion in myocardial tissue was quantified [74].
MM measurements for fluorescence and elastic scattering in the backward direction were used to study connective tissue regions of human cervical tissue [75][76]. Fluorescence linear and circular diattenuation, together with fluorescence linear and circular polarizance, were used as parameters derived from experimental MM. Significant differences were found between precancerous and normal tissues in the fluorescence polarimetric parameters—fluorescence linear diattenuation and linear polarizance—and in the diattenuation of the elastic scattering. These parameters are much lower at higher stages of precancer, which is explained by the loss of the anisotropic orientation of the molecular structures of collagens in precancerous connective tissues. A weaker, circular diattenuation arises from the presence of chiral moiety in collagen. The progression of precancer is accompanied by the destruction of collagen cross-links, which leads to loss of anisotropic organization and reduction of the diattenuation. It was concluded that it is possible to use fluorescence linear diattenuation and linear polarizance as new diagnostic parameters for detecting precancer.
It can be summarized that, although the MM contains rich, microstructural information about tissues, such information is difficult to obtain directly from the MM elements. To solve this problem, several methods have been proposed for transforming the MM elements into various groups of derived parameters that have a clearer physical and structural meaning [71][75][76][77][78].
The capabilities of polarimetric diagnostics can be tested on model tissue-like samples. The MM of soybean oil, which has a high degree of tissue-like properties, was studied [79].
4.4. Milk Composition Analysis and Food Quality Control
Among the needs of agriculture, milk quality control is of great importance. Information on the quantitative content of milk components (fat, proteins, lactose, somatic cells, progesterone, amino acids, etc.) is the basis for assessing milk quality and monitoring the nutritional balance and clinical condition of cows. In particular, the content of fat and protein is considered the main criterion for determining the market value of milk. Rapid analysis of milk composition is necessary for a prompt response to deviations in the parameters of the physiological state of animals and for timely correction of food rations if milk yield decreases. Additionally, milk analysis is an important part of the medical diagnostics which concern human milk for newborns [80]. Rapid milk testing can be performed by optical methods [80][81][82][83][84], among which MMP-based ones [81][82] are capable of multicomponent analysis. Using a setup which is actually an MM scatterometer, an empirical dependence of the MM elements of diluted milk on the amount of fat particles was obtained [81]. By solving the inverse problem for MM measurements, the distributions of fat and casein particles are retrieved; thereby, both fat and casein content in milk can be determined simultaneously from MM [82]. The ability of MMP to authenticate olive oil by linear dichroism and optical rotation of the circular birefringence retrieved from the MM of oil samples was revealed [85]. Changes in the depolarization of fresh and aged meat samples over time are clearly visible on MM polarimetric images and can serve as quantitative indicators for the non-invasive assessment of meat freshness [86].
4.5. Characterization of Soils and Fodders and Vegetation Monitoring
MMP finds application in the characterization of bulk materials such as soils and fodders. An MMP setup can be implemented as a unit for measuring the disperse composition in a robotic system that transforms soils into a stable, high-performance, organic, chemical bioreactor to better control the biomolecular interaction of nanoparticles and their adsorption by biological and mineral media [87]. MMs of microwave backscatter from bare soils are used to determine moisture content and surface irregularities [88]. Polarized IR laser scattering from sandy soil proved to be effective enough for evaluating the optical properties of sand particles and their size [89]. Information about vegetation properties can be obtained from the MM of vegetation-covered surfaces measured in bistatic scatter geometry by polarimetric radars [67][90]. Vegetation biomass can be derived from microwave polarized scattering returns using neural networks which are trained with vegetation scattering models [31]. The IR spectra of the MM elements measured for organic polymer films showed the presence of characteristic spectral lines in the block-diagonal elements of MM [53][54], which reveals the potential of IR MM spectroellipsometers for the analysis of organic compounds in soils and fodders.
4.6. Further Development of MMP Diagnostics Using Fiber Optics
Methods of non-destructive optical diagnostics, including those based on MMP, are constantly being developed. Fiber-optic devices have a special place in modern MMP instruments. To measure the MM, a multichannel PS-OCT with dynamic calibration improved by the use of a fiber-optic system was developed [91]. In the design of MMP devices, it is important to know the intrinsic polarization characteristics of the fiber-optic systems used. A virtual, generalized MM method for the characterization of a fiber-optic system with polarization-dependent elements and amplification was proposed [92]. This method allows obtaining data on polarization mode dispersion with high resolution and reduced noise level. An approach to measuring the MM for an optical fiber system with both birefringence and polarization-dependent loss or gain was tested [93]. Design examples of Mueller polarimetric endoscope and fiber Mueller polarimeter were described in [94].
References
- Fuller, G.G. Optical Rheometry of Complex Fluids; Oxford University Press: New York, NY, USA, 1995.
- Palberg, T.; Ballauff, M. Optical Methods and Physics of Colloidal Dispersions. In Proceedings of the International Workshop on Optical Methods and the Physics of Colloidal Dispersions held in Memory of Prof. Dr. Klaus Schätzel, Mainz, Germany, 30 September 1996; Steinkopff: Heidelberg, Germany, 1997.
- Xu, R. Particle Characterization: Light Scattering Methods; Kluwer Academic Publishers: New York, NY, USA, 2002.
- Mishchenko, M.I.; Travis, L.D.; Lacis, A.A. Scattering, Absorption, and Emission of Light by Small Particles; Cambridge University Press: Cambridge, UK, 2002.
- Doicu, A.; Wriedt, T.; Eremin, Y.A. Light Scattering by Systems of Particles; Springer: Berlin/Heidelberg, Germany, 2006.
- Azzam, R.M. Stokes-vector and Mueller-matrix polarimetry. J. Opt. Soc. Am. A 2016, 33, 1396–1408.
- Chipman, R.A.; Sornsin, E.A.; Pezzaniti, J.L. Mueller matrix imaging polarimetry: An overview. In Proceedings of the SPIE, International Symposium on Polarization Analysis and Applications to Device Technology, Yokohama, Japan, 12–16 June 1996; Yoshizawa, T., Yokota, H., Eds.; SPIE: Bellingham, WA, USA, 1996; Volume 2873, pp. 5–12.
- Arteaga, O.; Kahr, B. Mueller matrix polarimetry of bianisotropic materials. J. Opt. Soc. Am. B 2019, 36, F72–F83.
- Ghosh, N.; Soni, J.; Wood, M.; Wallenberg, M.; Vitkin, I. Mueller matrix polarimetry for the characterization of complex random medium like biological tissues. Pramana J. Phys. 2010, 75, 1071–1086.
- Tripathi, S.; Toussaint, K.C. Rapid Mueller matrix polarimetry based on parallelized polarization state generation and detection. Opt. Express 2009, 17, 21396–21407.
- Anastasiadou, M.; Hatit, S.B.; Ossikovski, R.; Guyot, S.; De Martino, A. Experimental validation of the reverse polar decomposition of depolarizing Mueller matrices. J. Eur. Opt. Soc. Rapid Publ. 2007, 2, 07018.
- Arwin, H.; Schoeche, S.; Hilfiker, J.; Hartveit, M.; Järrendahl, K.; Juárez-Rivera, O.R.; Mendoza-Galván, A.; Magnusson, R. Optical Chirality Determined from Mueller Matrices. Appl. Sci. 2021, 11, 6742.
- Boulvert, F.; Le Brun, G.; Le Jeune, B.; Cariou, J.; Martin, L. Decomposition algorithm of an experimental Mueller matrix. Opt. Commun. 2009, 282, 692–704.
- Liu, J.; Zhang, Q.; Huo, Y.; Wang, J.; Zhang, Y. An experimental study on light scattering matrices for Chinese loess dust with different particle size distributions. Atmos. Meas. Tech. 2020, 13, 4097–4109.
- Volten, H.; Jalava, J.P.; Lumme, K.; De Haan, J.F.; Vassen, W.; Hovenier, J.W. Laboratory measurements and T-matrix calculations of the scattering matrix of rutile particles in water. Appl. Opt. 1999, 38, 5232–5240.
- Diaspro, A.; Radicchi, G.; Nicolini, C. Polarized light scattering: A biophysical method for studying bacterial cells. IEEE Trans. Biomed. Eng. 1995, 42, 1038–1043.
- Mengüç, M.; Manickavasagam, S. Characterization of size and structure of agglomerates and inhomogeneous particles via polarized light. Int. J. Eng. Sci. 1998, 36, 1569–1593.
- Kolokolova, L.; Kimura, H.; Ziegler, K.; Mann, I. Light-scattering properties of random-oriented aggregates: Do they represent the properties of an ensemble of aggregates? J. Quant. Spectrosc. Radiat. Transf. 2006, 100, 199–206.
- Aiello, A.; Woerdman, J. Linear Algebra for Mueller Calculus. arXiv 2004, arXiv:Math-ph/0412061. Available online: https://arxiv.org/abs/math-ph/0412061 (accessed on 17 December 2004).
- Gil, J.J. Review on Mueller matrix algebra for the analysis of polarimetric measurements. J. Appl. Rem. Sens. 2014, 8, 081599.
- Ding, H.; Lu, J.Q.; Brock, R.S.; McConnell, T.J.; Ojeda, J.F.; Jacobs, K.M.; Hu, X.H. Angle-resolved Mueller matrix study of light scattering by B-cells at three wavelengths of 442, 633, and 850 nm. J. Biomed. Opt. 2007, 12, 034032.
- Van de Merwe, W.; Li, Z.Z.; Bronk, B.V.; Czégé, J. Polarized light scattering for rapid observation of bacterial size changes. Biophys. J. 1997, 73, 500–506.
- Le Gratiet, A.; Marongiu, R.; Diaspro, A. Circular Intensity Differential Scattering for Label-Free Chromatin Characterization: A Review for Optical Microscopy. Polymers 2020, 12, 2428.
- Pan, Y.L.; Aptowicz, K.; Arnold, J.; Cheng, S.; Kalume, A.; Piedra, P.; Wang, C.; Santarpia, J.; Videen, G. Review of elastic light scattering from single aerosol particles and application in bioaerosol detection. J. Quant. Spectrosc. Radiat. Transf. 2022, 279, 108067.
- Neuman, M. Angle Resolved Light Scattering in Turbid Media: Analysis and Applications. Ph.D. Thesis, Mid Sweden University, Härnösand, Sweden, 2011. Available online: http://urn.kb.se/resolve?urn=urn:nbn:se:miun:diva-13154 (accessed on 25 January 2011).
- Ghosh, N.; Vitkin, I.A. Tissue polarimetry: Concepts, challenges, applications, and outlook. J. Biomed. Opt. 2011, 16, 110801.
- Fanjul-Velez, F.; Samperio-Garcia, D.; Pereda-Cubian, D.; Arce-Diego, J.L. Mueller matrix group theory Formalism for tissue imaging polarimetry contrast increase. In Proceedings of the 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Lyon, France, 22–26 August 2007.
- Ramella-Roman, J.C.; Prahl, S.A.; Jacques, S.L. Three Monte Carlo programs of polarized light transport into scattering media: Part I. Opt. Express 2005, 13, 4420–4438.
- Ramella-Roman, J.C.; Prahl, S.A.; Jacques, S.L. Three Monte Carlo programs of polarized light transport into scattering media: Part II. Opt. Express 2005, 13, 10392–10405.
- Wang, X.; Yao, G.; Wang, L.V. Monte Carlo model and single-scattering approximation of the propagation of polarized light in turbid media containing glucose. Appl. Opt. 2002, 41, 792–801.
- Wang, L.F. Monte Carlo Simulation Model for Electromagnetic Scattering from Vegetation and Inversion of Vegetation Parameters. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2007. Available online: http://hdl.handle.net/1721.1/38923 (accessed on 28 September 2007).
- Tuchin, V.V. Polarized light interaction with tissues. J. Biomed. Opt. 2016, 21, 071114.
- Tuchin, V.V.; Zhu, D.; Genina, E.A. (Eds.) Handbook of Tissue Optical Clearing: New Prospects in Optical Imaging; CRC Press: Boca Raton, FL, USA, 2022.
- Lu, S.; Chipman, R. Interpretation of Mueller matrices based on polar decomposition. J. Opt. Soc. Am. A 1996, 13, 1106–1113.
- Shindo, Y.; Oda, Y.; Oshima, A.; Maeda, S. New type of CD spectropolarimeter with LD option. Rev. Sci. Instrum. 1993, 64, 1161–1168.
- Garcia-Caurel, E.; De Martino, A.; Drévillon, B. Spectroscopic Mueller polarimeter based on liquid crystal devices. Thin Solid Film 2004, 455–456, 120–123.
- Dubreuil, M.; Rivet, S.; Le Jeune, B.; Cariou, J. Snapshot Mueller matrix polarimeter by wavelength polarization coding. Opt. Express 2007, 15, 13660–13668.
- Protsenko, E.D.; Tymper, S.I.; Shkirin, A.V. Automated laser IR spectropolarimeter for surface Mueller matrix measurements. Instrum. Exp. Tech. 2011, 51, 268–274.
- Bueno, J.M. Polarimetry using liquid-crystal variable retarders: Theory and calibration. J. Opt. A Pure Appl. Opt. 2000, 2, 216–222.
- Suárez-Bermejo, J.C.; de Sande, J.C.G.; Santarsiero, M.; Piquero, G. Mueller matrix polarimetry using full Poincaré beams. Opt. Lasers Eng. 2019, 122, 134–141.
- Arteaga, O.; Freudenthal, J.; Wang, B.; Kahr, B. Mueller matrix polarimetry with four photoelastic modulators: Theory and calibration. Appl. Opt. 2012, 51, 6805–6817.
- Goldstein, D.H.; Chipman, R.A. Error analysis of a Mueller matrix polarimeter. J. Opt. Soc. Am. A 1990, 7, 693–700.
- Swamy, J.N.; Crofcheck, C.; Mengüç, M.P. Time dependent scattering properties of slow decaying liquid foams. Colloids Surf. A Physicochem. Eng. Asp. 2009, 338, 80–86.
- Laskarakis, A.; Logothetidis, S.; Pavlopoulou, E.; Gioti, M. Mueller matrix spectroscopic ellipsometry: Formulation and application. Thin Solid Films 2004, 455, 43–49.
- Mendoza-Galván, A.; Muñoz-Pineda, E.; Ribeiro, S.J.L.; Santos, M.V.; Järrendahl, K.; Arwin, H. Mueller matrix spectroscopic ellipsometry study of chiral nanocrystalline cellulose films. J. Opt. 2018, 20, 024001.
- Hilfiker, J.; Herzinger, C.; Wagner, T.; Marino, A.; Delgais, G.; Abbate, G. Mueller-matrix characterization of liquid crystals. Thin Solid Films 2004, 455, 591–595.
- Kupinski, M.; Li, L. Evaluating the Utility of Mueller Matrix Imaging for Diffuse Material Classification. J. Imaging Sci. Technol. 2020, 64, 60409.
- Juárez-Rivera, O.R.; Mauricio-Sánchez, R.A.; Järrendahl, K.; Arwin, H.; Mendoza-Galván, A. Shear-Coated Linear Birefringent and Chiral Cellulose Nanocrystal Films Prepared from Non-Sonicated Suspensions with Different Storage Time. Nanomaterials 2021, 11, 2239.
- Mendoza-Galván, A.; Li, Y.; Yang, X.; Magnusson, R.; Järrendahl, K.; Berglund, L.; Arwin, H. Transmission Mueller-matrix characterization of transparent ramie films. J. Vac. Sci. Technol. B 2020, 38, 014008.
- Fricke, D.; Becker, A.; Jutte, L.; Bode, M.; de Cassan, D.; Wollweber, M.; Glasmacher, B.; Roth, B. Mueller Matrix Measurement of Electrospun Fiber Scaffolds for Tissue Engineering. Polymers 2019, 11, 2062.
- Chen, C.; Chen, X.; Shi, Y.; Gu, H.; Jiang, H.; Liu, S. Metrology of Nanostructures by Tomographic Mueller-Matrix Scatterometry. Appl. Sci. 2018, 8, 2583.
- Deibler, L.L.; Smith, M.H. Measurement of the complex refractive index of isotropic materials with Mueller matrix polarimetry. Appl. Opt. 2001, 40, 3659–3667.
- Furchner, A.; Walder, C.; Zellmeier, M.; Rappich, J.; Hinrichs, K. Broadband infrared Mueller-matrix ellipsometry for studies of structured surfaces and thin films. Appl. Opt. 2018, 57, 7895–7904.
- Furchner, A.; Kratz, C.; Ogieglo, W.; Pinnau, I.; Rappich, J.; Hinrichs, K. Ultrasensitive broadband infrared 4 × 4 Mueller-matrix ellipsometry for studies of depolarizing and anisotropic thin films. J. Vac. Sci. Technol. B 2020, 38, 014003.
- Den Boer, J.H.W.G. Spectroscopic Infrared Ellipsometry: Components, Calibration, and Application; Technische Universiteit: Eindhoven, The Netherlands, 1995.
- Bunkin, N.F.; Shkirin, A.V.; Ninham, B.W.; Chirikov, S.N.; Chaikov, L.L.; Penkov, N.V.; Kozlov, V.A.; Gudkov, S.V. Shaking-Induced Aggregation and Flotation in Immunoglobulin Dispersions: Differences between Water and Water–Ethanol Mixtures. ACS Omega 2020, 5, 14689–14701.
- Lundblad, J.R.; Laurance, M.; Goodman, R.H. Fluorescence polarization analysis of protein-DNA and protein-protein interactions. Mol. Endocrinol. 1996, 10, 607–612.
- Maji, K.; Saha, S.; Dey, R.; Ghosh, N.; Haldar, D. Mueller Matrix Fluorescence Spectroscopy for Probing Self-Assembled Peptide-Based Hybrid Supramolecular Structure and Orientation. J. Phys. Chem. C 2017, 121, 19519–19529.
- Thermo Fisher Scientific. Molecular Probes Handbook. Fluorescence Polarization (FP). Available online: https://www.thermofisher.com/ru/ru/home/references/molecular-probes-the-handbook/technical-notes-and-product-highlights/fluorescence-polarization-fp.html (accessed on 18 July 2017).
- He, C.; He, H.; Chang, J.; Chen, B.; Ma, H.; Booth, M.J. Polarisation optics for biomedical and clinical applications: A review. Light Sci. Appl. 2021, 10, 194.
- Svensen, Ø.; Stamnes, J.; Kildemo, M.; Aas, L.; Erga, S.; Frette, Ø. Mueller matrix measurements of algae with different shape and size distributions. Appl. Opt. 2011, 50, 5149–5157.
- Badieyan, S.; Dilmaghani-Marand, A.; Hajipour, M.J.; Ameri, A.; Razzaghi, M.R.; Rafii-Tabar, H.; Mahmoudi, M.; Sasanpour, P. Detection and Discrimination of Bacterial Colonies with Mueller Matrix Imaging. Sci. Rep. 2018, 8, 10815.
- Chami, M. Importance of the polarization in the retrieval of oceanic constituents from the remote sensing reflectance. J. Geophys. Res. 2007, 112, C05026.
- Badieyan, S.; Ameri, A.; Razzaghi, M.R.; Rafii-Tabar, H.; Sasanpour, P. Mueller matrix imaging of prostate bulk tissues; Polarization parameters as a discriminating benchmark. Photodiagnosis Photodyn. Ther. 2019, 26, 90–96.
- Du, E.; He, H.; Zeng, N.; Sun, M.; Guo, Y.; Wu, J.; Liu, S.; Ma, H. Mueller matrix polarimetry for differentiating characteristic features of cancerous tissues. J. Biomed. Opt. 2014, 19, 076013.
- Liu, T.; Sun, T.; He, H.; Liu, S.; Dong, Y.; Wu, J.; Ma, H. Comparative study of the imaging contrasts of Mueller matrix derived parameters between transmission and backscattering polarimetry. Biomed. Opt. Express 2018, 9, 4413–4428.
- Wu, X.; Calabia, A.; Xu, J.; Bai, W.; Guo, P. Forest canopy scattering properties with signal of opportunity reflectometry: Theoretical simulations. Geosci. Lett. 2021, 8, 25.
- Ahmad, I.; Khaliq, A.; Iqbal, M.; Khan, S. Mueller matrix polarimetry for characterization of skin tissue samples: A review. Photodiagnosis Photodyn. Ther. 2020, 30, 101708.
- Smith, M.H.; Burke, P.D.; Lompado, A.; Tanner, E.A.; Hillman, L.W. Mueller matrix imaging polarimetry in dermatology. In Proceedings of the SPIE 3911, Biomedical Diagnostic, Guidance, and Surgical-Assist Systems II, San Jose, CA, USA, 3 May 2000.
- Jiao, S.; Yu, W.; Stoica, G.; Wang, L.V. Multiple-channel Mueller-matrix optical coherence tomography in biological tissue. In Proceedings of the Second Joint 24th Annual Conference and the Annual Fall Meeting of the Biomedical Engineering Society, Houston, TX, USA, 23–26 October 2002; Volume 3, pp. 2321–2322.
- Borovkova, M.; Trifonyuk, L.; Ushenko, V.; Dubolazov, O.; Vanchulyak, O.; Bodnar, G.; Ushenko, Y.; Olar, O.; Ushenko, O.; Sakhnovskiy, M.; et al. Mueller-matrix-based polarization imaging and quantitative assessment of optically anisotropic polycrystalline networks. PLoS ONE 2019, 14, e0214494.
- Ding, Z.; Liang, C.P.; Tang, Q.; Chen, Y. Quantitative single-mode fiber based PS-OCT with single input polarization state using Mueller matrix. Biomed. Opt. Express 2015, 6, 1828–1843.
- Guo, X.; Wood, M.; Vitkin, A.I. Angular measurements of light scattered by turbid chiral media using linear Stokes polarimeter. J. Biomed. Opt. 2006, 11, 041105.
- Ahmad, I.; Gribble, A.; Murtza, I.; Ikram, M.; Pop, M.; Vitkin, A. Polarization image segmentation of radiofrequency ablated porcine myocardial tissue. PLoS ONE 2017, 12, e0175173.
- Jagtap, J.; Chandel, S.; Das, N.; Soni, J.; Chatterjee, S.; Pradhan, A.; Ghosh, N. Quantitative Mueller matrix fluorescence spectroscopy for precancer detection. Opt. Lett. 2014, 39, 243–246.
- Soni, J.; Purwar, H.; Lakhotia, H.; Chandel, S.; Banerjee, C.; Kumar, U.; Ghosh, N. Quantitative fluorescence and elastic scattering tissue polarimetry using an Eigenvalue calibrated spectroscopic Mueller matrix system. Opt. Express 2013, 21, 15475–15489.
- Sheng, W.; Li, W.; Qi, J.; Liu, T.; He, H.; Dong, Y.; Liu, S.; Wu, J.; Elson, D.S.; Ma, H. Quantitative Analysis of 4 × 4 Mueller Matrix Transformation Parameters for Biomedical Imaging. Photonics 2019, 6, 34.
- He, H.; Zeng, N.; Li, D.; Liao, R.; Ma, H. Quantitative Mueller matrix polarimetry techniques for biological tissues. J. Innov. Opt. Health Sci. 2012, 5, 1250017.
- Firdous, S. Polarization Sensitive Optical Imaging and Characterization of Soybean Using Stokes-Mueller Matrix Model. In Soybean—Genetics and Novel Techniques for Yield Enhancement; Krezhova, D., Ed.; IntechOpen: London, UK, 2011.
- Veenstra, C.; Every, D.E.; Petersen, W.; van Goudoever, J.B.; Steenbergen, W.; Bosschaart, N. Dependency of the optical scattering properties of human milk on casein content and common sample preparation methods. J. Biomed. Opt. 2020, 25, 045001.
- Crofcheck, C.; Wade, J.; Swamy, J.N.; Aslan, M.M.; Mengüç, M.P. Effect of Fat and Casein Particles in Milk on the Scattering of Elliptically Polarized Light. Trans. ASAE 2005, 48, 1147–1155.
- Shkirin, A.V.; Ignatenko, D.N.; Chirikov, S.N.; Bunkin, N.F.; Astashev, M.E.; Gudkov, S.V. Analysis of Fat and Protein Content in Milk Using Laser Polarimetric Scatterometry. Agriculture 2021, 11, 1028.
- Lamelas, F.; Swaminathan, S. Optical absorption, scattering, and multiple scattering: Experimental measurements using food coloring, India ink, and milk. Am. J. Phys. 2020, 88, 137–140.
- Lehmann, P.; Osten, W.; Albertazzi Gonçalves, A.; Jain, P.; Sarma, S.E. Light scattering and transmission measurement using digital imaging for online analysis of constituents in milk. In Proceedings of the Optical Measurement Systems for Industrial Inspection, Munich, Germany, 21 June 2015.
- Derman, D.; Şenel, E.C.; Opar, E.; Ferhanoğlu, O.; Polat, Ö. Optical characterization of olive and sun flower oils via Mueller matrix polarimetry in combination with principal component analysis. J. Food Meas. Charact. 2021, 15, 2309–2317.
- Peyvasteh, M.; Popov, A.; Bykov, A.; Pierangelo, A.; Novikova, T.; Meglinski, I. Evolution of raw meat polarization-based properties by means of Mueller matrix imaging. J. Biophotonics 2021, 14, e202000376.
- Bunkin, N.F.; Glinushkin, A.P.; Shkirin, A.V.; Ignatenko, D.N.; Chirikov, S.N.; Savchenko, I.V.; Meshalkin, V.P.; Samarin, G.N.; Maleki, A.; Kalinitchenko, V.P. Identification of Organic Matter Dispersions Based on Light Scattering Matrices Focusing on Soil Organic Matter Management. ACS Omega 2020, 5, 33214–33224.
- Oh, Y.; Sarabandi, K.; Ulaby, F.T. Semi-empirical model of the ensemble-averaged differential Mueller matrix for microwave backscattering from bare soil surfaces. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1348–1355.
- Zallat, J.; Stoll, M.P. Polarized bidirectional scattering by bare soils. J. Opt. A Pure Appl. Opt. 2000, 2, 169.
- Jin, Y.Q. Theoretical Modeling for Polarimetric Scattering and Information Retrieval of SAR Remote Sensing. In Advances in Geoscience and Remote Sensing; IntechOpen: London, UK, 2009.
- Jiao, S.; Yu, W.; Stoica, G.; Wang, L. Optical-fiber-based Mueller optical coherence tomography. Opt. Lett. 2003, 28, 1206–1208.
- Dong, H.; Shum, P.; Gong, Y.D.; Yan, M.; Zhou, J.Q.; Wu, C.Q. Virtual Generalized Mueller Matrix Method for Measurement of Complex Polarization-Mode Dispersion Vector in Optical Fibers. IEEE Photonics Technol. Lett. 2007, 19, 27–29.
- Dong, H.; Shum, P.; Yan, M.; Zhou, J.Q.; Ning, G.X.; Gong, Y.D.; Wu, C.Q. Measurement of Mueller matrix for an optical fiber system with birefringence and polarization-dependent loss or gain. Opt. Commun. 2007, 274, 116–123.
- Qi, J.; Elson, D.S. Mueller polarimetric imaging for surgical and diagnostic applications: A review. J. Biophotonics 2017, 10, 950–982.
More
Information
Subjects:
Instruments & Instrumentation
Contributors
MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register
:
View Times:
1.6K
Revisions:
2 times
(View History)
Update Date:
20 Jun 2022
Notice
You are not a member of the advisory board for this topic. If you want to update advisory board member profile, please contact office@encyclopedia.pub.
OK
Confirm
Only members of the Encyclopedia advisory board for this topic are allowed to note entries. Would you like to become an advisory board member of the Encyclopedia?
Yes
No
${ textCharacter }/${ maxCharacter }
Submit
Cancel
Back
Comments
${ item }
|
More
No more~
There is no comment~
${ textCharacter }/${ maxCharacter }
Submit
Cancel
${ selectedItem.replyTextCharacter }/${ selectedItem.replyMaxCharacter }
Submit
Cancel
Confirm
Are you sure to Delete?
Yes
No




