
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Charles Roberto Telles | + 2037 word(s) | 2037 | 2019-01-14 16:24:21 | | | |
| 2 | Charles Roberto Telles | Meta information modification | 2037 | 2019-01-16 16:53:34 | | | | |
| 3 | Peter Tang | -25 word(s) | 2012 | 2020-10-30 10:08:52 | | |
Video Upload Options
How parameters such as interaction, iteration, frequency of iteration and time can express in a simple manner a nonlinear dynamics?
Considering a system with stationary PDF and ergodic properties, the mathematical framework reveals a constant oscillation of information flow in the system. Those parameters mentioned before can start chaotic process in the previous system generating infinite random sequences as Per Martin-Löf suggested in his work "Complexity oscillations in infinite binary sequences". In this way the non ergodic properties of system express observable oscillations in which time lengths regulations can be used as a tool for PDF constraint and phase space formations.
1. General description
When considering Bernoulli sequences and probabilistic system analysis, any PDF (probability density function) originated from time sequenced variables can present geometric properties leading the event to the time regulated dynamics[1]. This condition can be situated when variables are time dependent and system evolution is also dependent from the previous conditions of any interaction, iteration and frequency of interaction aspects of variables[2][3].
This feature is not found in Markov Chains or queuing theory as a whole, but some logical propositions of both knowledge can result into the time regulated dynamics[4][5][6]. It was found that the geometrical properties of nature cannot be periodical or express quasi periodic properties if the time of the variable's iteration and interaction not be synchronous in a way chaotic possibilities can be organized towards new phase states[7][8].
It is considered geometrical properties of nature as Benoulli's sequences assuming PDF as regulated by time lengths of the sequences. In this way, even random events can happen to express dynamics. The constraints caused by time close a pathway leading probabilistic systems to pre consecutive phase spaces[9]. For this example, figure 1 represents generally speaking two types of information flow where the example A, time is constant and information follows that path as well.
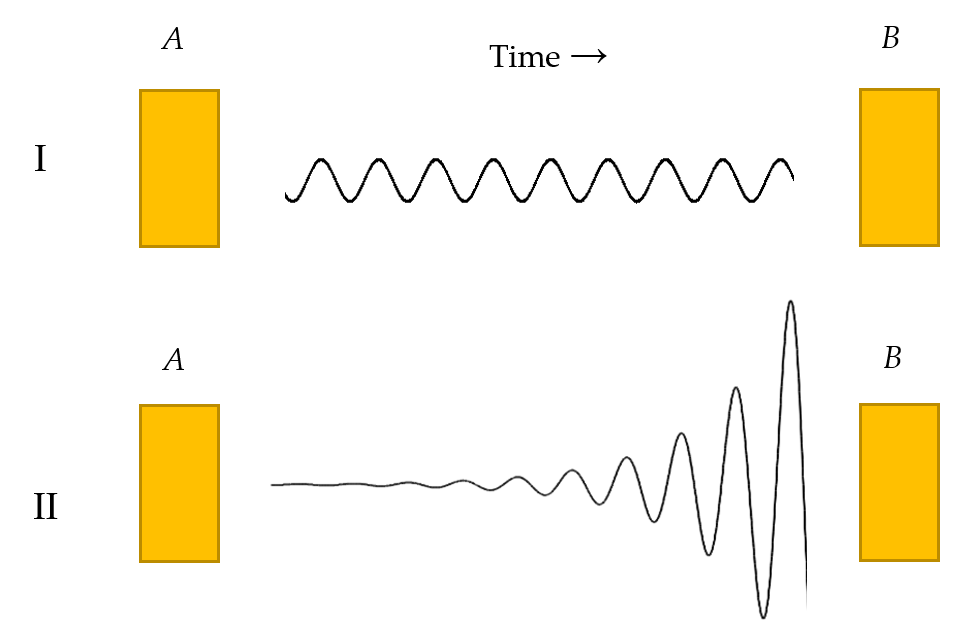
Figure 1. Information flow at geometric variables (I) and not geometric variables (II).
At example B, time is regulated and information flow assumes distinct pathways leading event to higher oscillations than the previous state.
2. Mathematical framework
Theorem 1. Considering the systems as ideal and not possible of having non-observable variables that directly influence consumption behavior. For both systems (school A and B) for the first 15 seconds (Y), there is the possibility of a student consuming the resource ( x1), and the opposite time and space effect that none will consume it ( x2), (without possibility of the same individual consuming again). Indicating the consumption of resources by an individual as “1” and not consumption, “0", in a given number K of dependent iterations (a function of time), the constant flow of variables is contained in the time, as it is indicated in the following Equation (1):
(1) 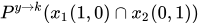
After the 15 seconds end, there is the second expression of the system as a potential possibility of another student repeat the starting condition. Resulting as,
Lemma 1. Given the probabilities, the events (variables) of success p and failure q, are considered as 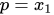 and
and 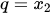 , where the variables p and q are dependent and not identically distributed (not iid), and we get the following probability of the event:
, where the variables p and q are dependent and not identically distributed (not iid), and we get the following probability of the event: 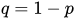 . The odds of the event following the given probability can be set as:
. The odds of the event following the given probability can be set as:
(2) 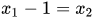 with 50% chance and
with 50% chance and 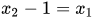 with 50% chance
with 50% chance
Proof of Lemma 1. Since, the system has a geometrical property, for all n binary vectors  , it obtains 100% odd for any time length as Equation (3):
, it obtains 100% odd for any time length as Equation (3):
(3) 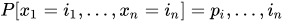
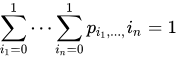
When the probabilities between the two systems are identical and not observable in Bernoulli's method in terms of probability density function regarding the behavior of the two systems as compared to each other in the function Y, it can be of use considering the frequency in which variables x1 and x2 have their iterated behavior regulated by the time. Therefore, to conceive the analysis as information entropy of the system, the variables considered assume an evolution on time in bits[10].
As time Tk passes, there is a growth of the variable x1 and x2 revealing binary sequences that repeat cumulatively and asymmetrically on time length 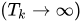 , according to Table 1:
, according to Table 1:
Table 1. Bits distribution over time.

The sequences originated by bits of information and distributed by variables with geometrical properties can be described by the next Equation (5) and Figure 2:

Figure 2. Schematic of bit evolution over time.
(4) 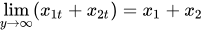
Where, in other way it can be represented as a combination of variables defined as: 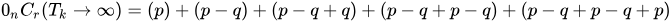 , and so on.
, and so on.
Proof of Theorem 1: The probability of the infinite sequences of iterations set to happen in values 0 and 1 is constant as k becomes infinite and remains always in the given proportion of 50%[1]. Where,
(5) 
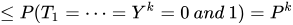
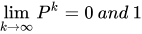
Both variables assumes in ideal condition an evolution on time presenting constant probability and oscillation (Figure 3). Regarding the odds of 50% for the sequence evolution, for realistic conditions, it is not correct to assume that value neither for the theoretical investigation of this article, in which it was considered a constant flow of variables performing 100% constant sequencing. For that point, the article describe the event for the most ideal behavior of variables (deterministic) when considering it as the parameter, a model, in which for real life situations, analogously, it is possible to exclude the interference of multiple other variable's effects from event, whose presence in it have the punctual potential of affecting the final results.
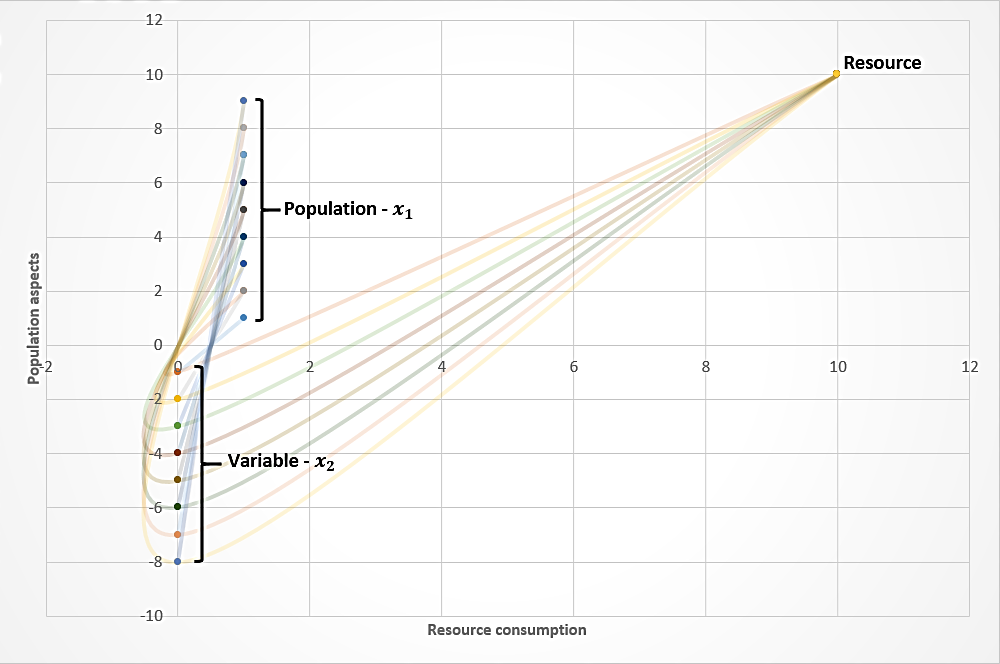
Figure 3. Deterministic evolution of water consumption by population over time.
In Figure 3, the x axis represents the resource consumption trajectory while y positive axis represent population interaction (x1) with resource and negative y axis, the variable x2. x2 is expressed in the same manner as x1 in the time function Y and as a necessary effect caused by resource consumption and individual interaction. The information sequence, from the left to the right, in which the variable x1 and x2 are expressed reveal common periodic oscillations (constant patterns of event starting conditions), in which regardless of the size of the sequence, the results will always be the same. Thus, the maximum information entropy[11] of the system is finite or infinitely constant, but asymmetric on time length regarding the alternated presence of variables x1 and x2 set to happen. The evolution of iterations (Y) perform a periodic oscillation or as a geometric variable L, consisting of a constant odd of events on time, whatever the time length chosen from the sequence.
Theorem 2. Following this path, the ratio of x1 to x2 is shown as increasing, but asymmetric in the length of Y function as a geometric variable L:
(6) 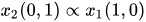
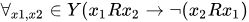
In this sense, it is possible to affirm that both the population of 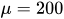 and
and 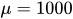 will have consumption and idle time, defined by Y, in which the variable x1 and x2 will not have different expressions of probability and maximum entropy of information for both populations. Otherwise, a result is obtained where time affects event influencing number of sequences to happen defined by the following Equation of Cauchy[12]:
will have consumption and idle time, defined by Y, in which the variable x1 and x2 will not have different expressions of probability and maximum entropy of information for both populations. Otherwise, a result is obtained where time affects event influencing number of sequences to happen defined by the following Equation of Cauchy[12]:

where,
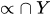
Produces dynamical properties in the event as:
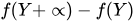
Resulting in,
(7) 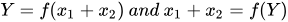
The geometric variable L affects infinitely every time 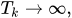 , expressing turn shifts between variable x1 and x2. The geometric variable L expresses no probability functions, except if determined by Y, in which this article aims to associate with resources management within a system as a simulator of resources distribution management. This is represented as:
, expressing turn shifts between variable x1 and x2. The geometric variable L expresses no probability functions, except if determined by Y, in which this article aims to associate with resources management within a system as a simulator of resources distribution management. This is represented as:
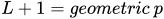
where L is equal to,
(8) 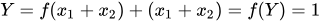
The probability of Lk is equal to the variables x1 and x2 in its probabilistic expressions as follows:
(9) with 50% chance and 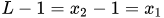 with 50% chance
with 50% chance
Proof of Theorem 2. For variable L with geometric distribution of 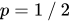 , where,
, where, 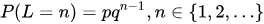 ; the entropy of L in bits is: [13]
; the entropy of L in bits is: [13]
(10) 
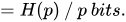
If  , then
, then  bits.
bits.
Some patterns are produced as constant features of the system. They are the probability and entropy of x1, x2 and geometric p. But, other variables influence the event, the number of iterations (Y). This effect, as represented in Figure 4, counts towards amount of resources available and population size. Y can be represented for managerial purposes as a controlling tool in which types of resources management can be achieved.
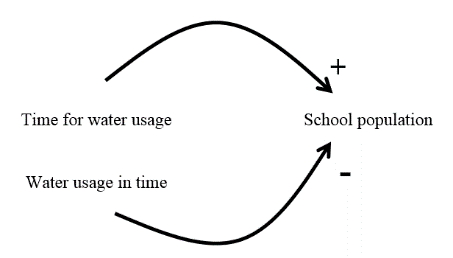
Figure 4. Nonlinearity effects caused by time according to Figure 5.
As observed in Figure 5, oscillations goes to infinity as article stated, but if not infinite, it is possible to observe the information evolution of sequences, generating PDF, being possible to regulate those dynamical properties of event by considering aspects of time, iteration, interaction and the frequency of iteration[2][14].
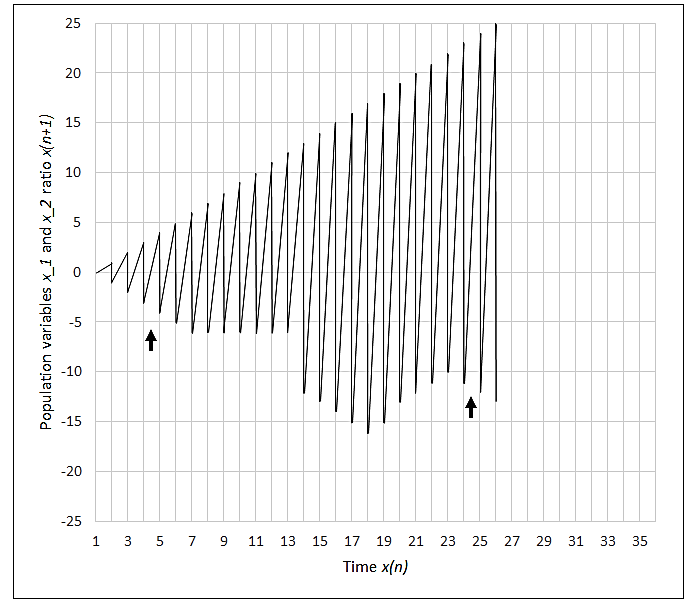
Figure 5. Time series of population variables x1 and x2 expressing disproportionality for population-resource ratio. The asymmetrical pattern shows recurrence at original state (indicated arrows) and time regulation equilibrium.
If an event of Figure 5 were represented by time series analysis, it would generate constant, but alternated phase states of variables behaviors. This situation can be represented by Figure 6 in the time series graph.
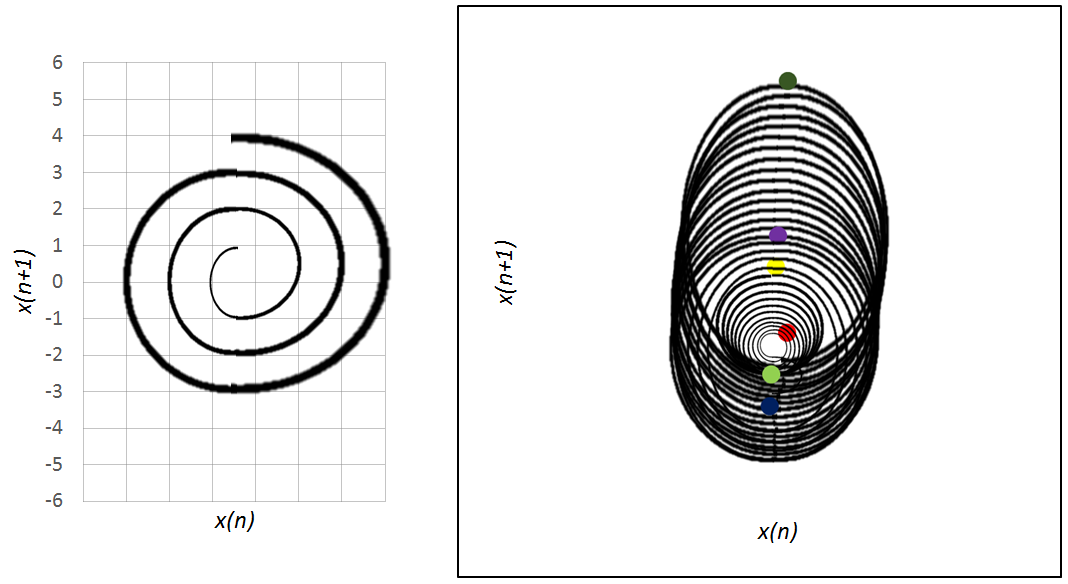
Figure 6 and 7. To the left, the representation of Figure 6 and to the right, Figure 7. In this view, it is possible to see specific phases of event of Figure 7 that are marked with color circles. Red circle, event start. Light green, time regulation. Blue circle, x2 saturation. Yellow, chaotic phase. Purple, population growth and variable variable x2 reduction. Dark green, recurrence of variable x2.
3. Conclusion
The analysis of information flow by binary sequences of Bernoulli regulated by time lengths can be of use to predict the behavior of nonlinear systems in a continuous way, allowing for the manager to visualize the events in their particularities of oscillations behaviors. This way, low amount of information in a non-linear system, as Shannon already stated, gives high probability and high amount of information, gives low probability. This statement can be forwarded accordingly to time regulations to investigate oscillation properties of systems of which in low amount of information, the time effects are unable to produce high oscillation properties. On the contrary, high amount of information that is associated with time regulations, can result in high output of oscillations. The analysis does not take place as an exhaustive methodology for understanding these types of events. However, logical propositions arising from such analyzes can be useful for planning, monitoring, and controlling complex systems in order to reduce the estimated risks for these events. Phase space of event investigated in this article was no performed. Though it was mentioned in results section, further
studies are required. It is suggested to study behavior of event in its recurrence plots and establish more specific relations with subject fields of knowledge.
Also the article scope of investigation brings a glance of how time is related to phenomena where diverse variables that are located in a chain of events, in which, probabilistic functions can assume an evolution of density and retrocede in its own properties regulated by time lengths. These densities evolutions promote together with other variables, increasing margins of possible outcomes in a complex chain of events, giving the whole view of deterministic to the chaotic control of events in duality transformations for each pathway of the event. In this way, it is possible to regulate through time the frequencies in which iterations assume the main role of possible oscillations in the event, thus reducing the non-ergodicity of the system as a whole. This statement was performed in theoretical view, using water-population ratio of interaction, iteration, frequency of iteration, and time regulations. It is considered as an approach for future researches with the same characteristics of this study. The objective to finish this approach is related to not only use the last paragraph statement as an indicator for a manager, but also have the possibility of measure the dynamics of all variable's information flow leading to the capability of manipulating events and therefore, increasing the precision and margin of possible outcomes.
The last, but inferred conclusion, at first can be considered as an unobservable factor, the analysis of conditions of which a system is, when the number of iterations through time, affects the expression of possible outcomes (pathways) of the event changing its internal probabilities or entropy flows. But, in this sense, the flow of information is a function of interaction, iteration, frequency of iterations, and time regulations effect rather than potential entropy of information presented in the observed event or variables at their starting conditions. This view can lead to the new possibilities of controlling deterministic to chaotic behavior in nonlinear phenomena.
References
- Tsitsiklis, J. Bernoulli Process: Probabilistic Systems Analysis and Applied Probability . MITOPENCOURSEWARE. Retrieved 2019-1-14
- Charles Roberto Telles; Geometrical Information Flow Regulated by Time Lengths: An Initial Approach. Symmetry 2018, 10, 645, 10.3390/sym10110645.
- Kevin Knuth; Deniz Gençağa; William Rossow; A Recipe for the Estimation of Information Flow in a Dynamical System. Entropy 2015, 17, 438-470, 10.3390/e17010438.
- Guercio, R.; Magini, R.; Pallavicini, I.; Instantaneous residential water demand as stochastic point process. WIT Transactions on Ecology and the Environment 2001, 48, 10, 10.2495/WRM010121.
- Steven G. Buchberger; Lin Wu; Model for Instantaneous Residential Water Demands. Journal of Hydraulic Engineering 1995, 121, 232-246, 10.1061/(asce)0733-9429(1995)121:3(232).
- Yangyang Tao; Shucheng Yu; Junxiu Zhou; Information Flow Queue Optimization in EC Cloud. 2018 International Conference on Computing, Networking and Communications (ICNC) 2018, 1, 888-892, 10.1109/iccnc.2018.8390367.
- Uzi Harush; Baruch Barzel; Dynamic patterns of information flow in complex networks. Nature Communications 2017, 8, 2181, 10.1038/s41467-017-01916-3.
- C. E. Shannon; A mathematical theory of communication. ACM SIGMOBILE Mobile Computing and Communications Review 2000, 5, 3, 10.1145/584091.584093.
- Reik V. Donner; Michael Small; Jonathan Donges; Norbert Marwan; Yong Zou; Ruoxi Xiang; Jürgen Kurths; RECURRENCE-BASED TIME SERIES ANALYSIS BY MEANS OF COMPLEX NETWORK METHODS. International Journal of Bifurcation and Chaos 2011, 21, 1019-1046, 10.1142/s0218127411029021.
- Mézard, M.; Montanari, A.. Information, Physics and Computation; Oxford University Press: Corby, UK, 2009; pp. 568.
- Turkay Baran; Nilgun B. Harmancioglu; Cem Polat Cetinkaya; Filiz Barbaros; An Extension to the Revised Approach in the Assessment of Informational Entropy. Entropy 2017, 19, 634, 10.3390/e19120634.
- Augustin-Louis Cauchy; COURS D'ANALYSE DE L'ÉCOLE ROYALE POLYTECHNIQUE. Oeuvres complètes 1969, 3, 17-30, 10.1017/cbo9780511702525.003.
- Cover, T.M.; Thomas, J.A.. Elements of Information Theory; 2nd ed., Eds.; Willey-Interscience: Hoboken, NJ, USA, 2006; pp. 750.
- Per Martin-Löf; Complexity oscillations in infinite binary sequences. Probability Theory and Related Fields 1970, 19, 225-230, 10.1007/bf00534110.




