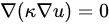A thermal bridge is a component of a building that is characterized by a higher thermal loss compared with its surroundings. Their accurate modeling is a key step in energy performance analysis due to the increased awareness of the importance of sustainable design. Thermal modeling in architecture and engineering is often not carried out volumetrically, thereby sacrificing accuracy for complex geometries, whereas numerical textbooks often give the finite element method in much higher generality than required, or only treat the case of uniform materials. Despite thermal modeling traditionally belonging exclusively to the engineer’s toolbox, computational and parametric design can often benefit from understanding the key steps of finite element thermal modeling, in order to inform a real-time design feedback loop. In this entry, these gaps are filled and the reader is introduced to all relevant physical and computational notions and methods necessary to understand and compute the stationary energy dissipation and thermal conductance of thermal bridges composed of materials in complex geometries. The overview is a self-contained and coherent expository, and both physically and mathematically as correct as possible, but intuitive and accessible to all audiences. Details for a typical example of an insulated I-beam thermal bridge are provided.
Building energy performance simulation, modeling and optimization has become an ever more important discipline at the multidisciplinary junction between building physics, design, architecture, engineering, numerical mathematics and optimization. Soaring energy costs and an increased awareness of the urgency of sustainability amid a global energy crisis have led to growing interest far beyond the original scope of an engineering sub-discipline. Physically, heat transfer is described by the heat equation—a century old and well studied partial differential equation (henceforth abbreviated PDE). In principle, it determines the heat distribution in a given geometry, for given material constants and boundary conditions, either in a time-dependent or time-independent manner. In practice, however, an accurate solution requires a finite element discretization of the heat equation. A finite element solution solves an approximation to the heat equation on a tetrahedralization of the input domain; see Zienkiewicz et al.
[1] for a general introduction to finite element (FE) methods; Ciarlet
[2] for an introduction to FE on the particular class of elliptic PDEs relevant here, and Wilson and Nickell
[3], Lewis et al.
[4] for the application of FE to thermal modeling. Effectively, this places simulation and modeling at the heart of every modern building performance simulation.
There is no treatment in the literature that coherently covers the engineering aspects together with the full three-dimensional FE method in a way that is accessible to an audience from, say, a design background. Most expositions focus either on basic one-dimensional quantities such as the
U-value
[5], on numerical methods for the full 3D heat transfer, or on computational design in view of architectural and artistic aspects
[6]. A thermal bridge is defined as a building component with particularly high thermal loss; as such, they are the most important objects of modeling
[7][8]. This entry aims to outline a complete introduction to put the reader in a position to understand all steps necessary to compute the energy loss incurred by a particular thermal bridge situation in design.
As a rule of thumb, heating costs constitute one of the largest shares of the per capita energy profile of the average Western inhabitant of moderate latitudes. For example, it is estimated that the entire average annual primary energy consumption in developed countries is roughly 100–200 GJ per capita
[9]. On the other hand, for example in Germany, the annual per capita heating energy profile is estimated to be more than 3000 kWh ≈ 10 GJ per year
[10]. Thus, a considerable fraction of about 5–10 percent of the energy is spent on heating alone. This places the heating energy profile among the top private household budget items.
Consequently, there are plenty of legal incentives, policies and regulations aimed at instigating energy efficiency certifications in most countries in the middle latitudes. Energy certification, consulting, contracting, and modernization have all become their own industry segments. This increased pressure on home owners, real estate agents and developers has recently led to the previously unthinkable situation where the energy certificate has the highest or one of the highest impacts on a real estate’s (rental) value, among all value predictors
[11].
Apart from these environmental and monetary incentives for having good insulation, thermal performance and insulation are, of course, highly relevant in regards to building safety due to their importance for vapor condensation and mold prevention. Consequently, estimating and optimizing a building’s energy performance has become one of the cornerstones of sustainable architecture, modernization, renovation, maintenance and building safety.
There is an abundance of commercial and non-commercial FE software packages available on the market. It would seem difficult to even attempt to cite a comprehensive list of the most important ones, due to the far-reaching impact they have, the multitude of application scenarios, and the long amount of time these packages have already been under development for. For example, one of the most popular commercial software packages capable of modeling thermal conductance is ANSYS
[12], and one of the most popular open source software packages if Freefem++
[13]. However, it is often desirable to understand and implement a basic FE algorithm from scratch, rather than treating the FE method as a black box. This entry aims to introduce students of all the aforementioned disciplines, in particular those without prior exposure to FE methods and computational physics from scratch to a state where the reader could, at least in principle, implement their own FE solution. In this text, no prior exposure to computational design, programming, or mathematics beyond an early undergraduate level are assumed. In particular, it will be explained how the seemingly arcane physical description of heat transfer translates into an amenable pseudo-code which can readily be employed and adapted to more specialized optimization questions.
Most architecturally inspired texts, or even those for engineering students, tend not to describe the full volumetric heat equation, and focus on one or two-dimensional case studies
[14], or even just a description of insulation indicators such as
U-values, avoiding differential equations altogether. On the other hand, mathematically oriented textbooks tend to ignore materials altogether, and just treat the “heat equation” in the form of

where
u is the temperature distribution and
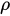
is a heat source term,
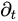
is the time derivative, and

is the Laplacian
[15]. However, the relevant equation for use in our case is when
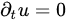
is the steady state or stationary property and
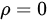
In fact, there is usually no heating inside the thermal bridge. In contrast, the term
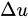
needs to be replaced with the slightly more general expression
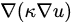
In this entry, the following convention is used: The operator ∇ applied to a scalar field such as u is the gradient of the scalar field, such as the temperature gradient, and ∇ applied to a vector field, such as the heat flux, is the divergence of the vector field. The reader is invited to recall that the divergence of a vector field is a scalar field that describes how much the vector field converges or diverges.
These variations of the heat equation will be explained in
Section 3.2. For the purely mathematical and theoretical treatment, omitting
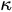
from the picture makes almost no difference, but here, all the material properties are expressed through, and have an impact on the modeling, in terms of their conductivity
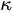
All of the information about the materials is in the quantity
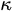
It is isotropic but also non-uniform and hence can not be “pulled in front” as a simple constant number. Therefore, one can not simplify the term
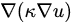
to
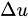
as almost all mathematically oriented textbooks tend to do.
In this sense, the PDE literature equation is both an oversimplification of material continuity and a complication of time dependence. Due to these small differences, the classical PDE literature is almost useless for the architect and engineer who focuses on modeling thermal bridges. The passage from the PDE

to the PDE
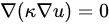
—Equation (
2) below—makes both the analytical understanding and the practical numerical treatment much easier to comprehend, but it is quite different and not entirely trivial.
Similarly, there do not seem to be many treatments of FE methods for this particular case. One of the reasons being that in an engineering context, FE methods are most often associated with structural engineering solving the linear elasticity equations—or simplifications derived from it. Likewise, the second most frequent field of PDEs is computational fluid dynamics. Consequently, the term “FE methods” is sometimes mistakenly understood to refer only to structural analysis or computational fluid dynamics.
It should be noted that in the last few years a large amount of work was dedicated to “mesh-free methods”, with the heat equation being a prominent example in the context of geometry processing
[16]. However, in the context of actual engineering, FE methods remain the gold standard and method of choice due to their proven accuracy and versatility. The same holds true for the finite difference method
[17]—as opposed to the FE method. The former places a grid over the entire domain and solves the heat equation with a simple differencing scheme. However, the drawback of the finite difference method is the scale dependency, and the fact that complex geometries can hardly be resolved accurately with an equi-spaced grid. The finite difference method will thus not be treated.
Likewise, instationary (time-dependent) computations will not be treated, nor will those that require taking radiative effects into account. For instance, the treatment of overheating in summer requires taking day-night temperature curves, as well as radiative transmission and absorption characteristics into account. Even though these considerations tend to have a large impact on the design of glass facades as well as shadow casting interior components, etc., these topics go well beyond the accurate treatment of thermal bridges and their insulation. Thus, since descriptions of the FE method just for the relevant Equation (2) are rare, this gap will be filled in this entry.
This entry does not aim to enable the reader to draft DIN-conformant engineering reports. For instance, the specifications of effective thermal surface resistances, as required, for example, in DIN 4180-2
[18] are technically intricate and very country-specific. Instead, this entry will assume the extreme case where the room facing surface is kept at 20 °C and the outward facing surface is kept at −13.1 °C as is often done in Germany and Austria. Compared with the computation that takes surface resistances into account, this gives a conservative bias. Such a bias is often acceptable for a designer or architect who wishes to estimate the thermal feasibility during the design process. It is possible to implement the class of algorithms described in this entry in such a way that it runs in real-time. The most important ISO norms relevant for thermal modeling will be referenced in Section 4.5. Further details on norms, reporting, regulations, and certification would go beyond the scope of the entry.
One of the most important applications of thermal modeling is the simulation of hygrothermal properties: water vapor diffusion and condensation; see Taylor et al.
[19], Gasparin et al.
[20] and the references therein.
The entry is structured as follows. Section 2 gives all of the relevant definitions. Then, the physical and mathematical concepts will be introduced as thoroughly as necessary and as concisely as possible in Section 3 and some analytical examples of the heat equation will also be provided. The actual FE formulation is described in Section 4. Section 5 presents a typical case study of an I-beam penetrating a wall. Then, the entry will be finish with a conclusion in Section 6.

 where u is the temperature distribution and
where u is the temperature distribution and 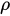 is a heat source term,
is a heat source term, 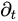 is the time derivative, and
is the time derivative, and  is the Laplacian [15]. However, the relevant equation for use in our case is when
is the Laplacian [15]. However, the relevant equation for use in our case is when 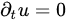 is the steady state or stationary property and
is the steady state or stationary property and 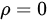 In fact, there is usually no heating inside the thermal bridge. In contrast, the term
In fact, there is usually no heating inside the thermal bridge. In contrast, the term 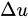 needs to be replaced with the slightly more general expression
needs to be replaced with the slightly more general expression 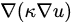
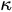 from the picture makes almost no difference, but here, all the material properties are expressed through, and have an impact on the modeling, in terms of their conductivity
from the picture makes almost no difference, but here, all the material properties are expressed through, and have an impact on the modeling, in terms of their conductivity 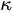 All of the information about the materials is in the quantity
All of the information about the materials is in the quantity 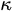 It is isotropic but also non-uniform and hence can not be “pulled in front” as a simple constant number. Therefore, one can not simplify the term
It is isotropic but also non-uniform and hence can not be “pulled in front” as a simple constant number. Therefore, one can not simplify the term 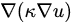 to
to 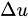
 to the PDE
to the PDE