Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Kai He
 -- 1999 2022-05-18 07:37:45 |
2 format correct
Vivi Li
 -26 word(s) 1973 2022-05-19 04:56:51 |

Video Upload Options

Do you have a full video?
Send video materials Upload full video

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
He, K.; Zhu, N.; Wu, J.; Zhu, C. Efficiency of Industrial Based on Network DEA Method. Encyclopedia. Available online: https://encyclopedia.pub/entry/23043 (accessed on 17 May 2024).
He K, Zhu N, Wu J, Zhu C. Efficiency of Industrial Based on Network DEA Method. Encyclopedia. Available at: https://encyclopedia.pub/entry/23043. Accessed May 17, 2024.
He, Kai, Nan Zhu, Jiang Wu, Chuanjin Zhu. "Efficiency of Industrial Based on Network DEA Method" Encyclopedia, https://encyclopedia.pub/entry/23043 (accessed May 17, 2024).
He, K., Zhu, N., Wu, J., & Zhu, C. (2022, May 18). Efficiency of Industrial Based on Network DEA Method. In Encyclopedia. https://encyclopedia.pub/entry/23043
He, Kai, et al. "Efficiency of Industrial Based on Network DEA Method." Encyclopedia. Web. 18 May, 2022.
Efficiency of Industrial Based on Network DEA Method
Edit
This entry is adapted from the peer-reviewed paper 10.3390/su14095264

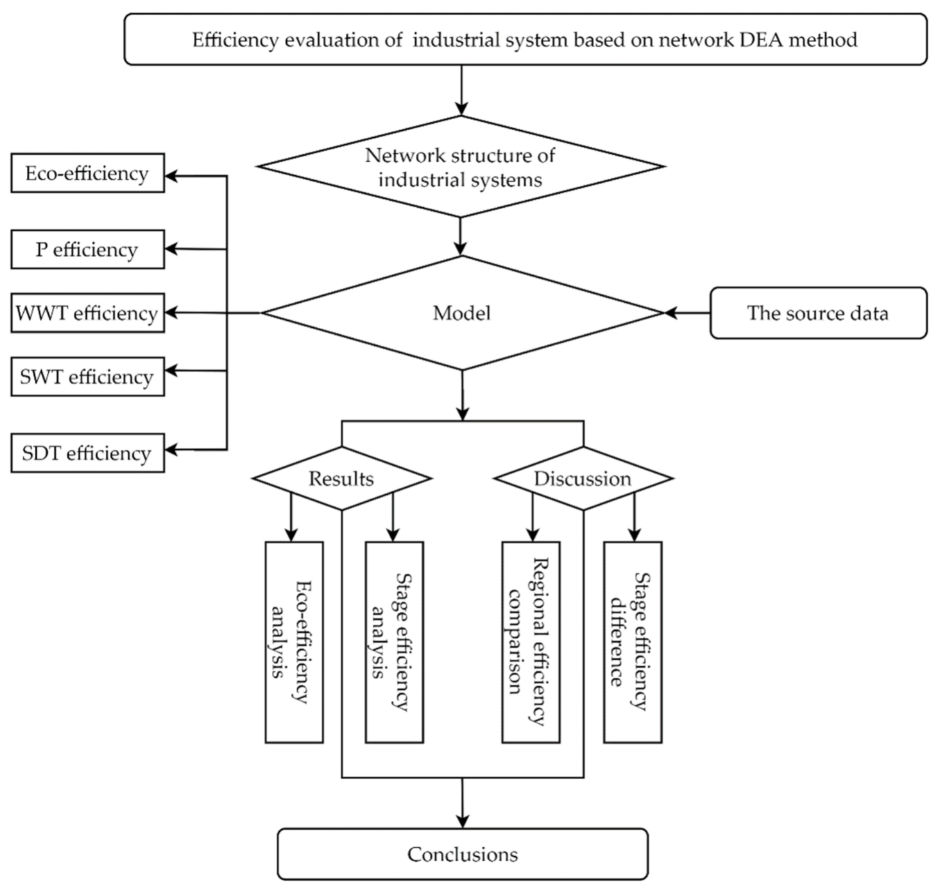
There are two main methods to study the efficiency of industrial sectors. The first is parametric method represented by stochastic frontier method (SFA). The other is the more widely used non-parametric method represented by data envelopment analysis (DEA), which makes up for the shortcomings of the SFA method. It does not need to specify a certain functional relationship between input and output. The operation process of the Chinese provincial industrial system consists of four stages, namely the production (P) stage, wastewater treatment (WWT) stage, solid waste treatment (SWT) stage, and sulfur dioxide treatment (SDT) stage. Based on this structure, a four-stage data envelopment analysis (DEA) model is developed to evaluate the eco-efficiency, production efficiency, wastewater treatment efficiency, solid waste treatment efficiency, and sulfur dioxide treatment efficiency of provincial industrial systems in China, considering the undesirable output and variable returns to scale (VRS). 

data envelopment analysis industrial system wastewater solid waste sulfur dioxide

1. Introduction

Since its reform and opening up, and with the rapid development of industrialization, the Chinese economy has made remarkable achievements. However, behind this achievement, China has paid a huge energy and environmental price. The extensive economic development model with high energy consumption and high emissions has brought energy shortages and environmental pollution to China. As the world’s largest energy consumer and greenhouse gas emitter, China accounts for 23% of the world’s energy consumption, according to data released by the BP Statistical Yearbook of World Energy. Only 29.3% of China’s 338 major cities meet the air quality standards recommended by the Ministry of Ecology and Environment, according to the 2017 China Environmental Status Bulletin [1]. For this reason, the Chinese government has taken drastic measures to control air pollution. For example, The State Council issued the Air Pollution Prevention and Control Action Plan (2013) and the Three-year Action Plan to Win the Battle against Blue Skies (2017). Currently, air pollution in China has attracted widespread attention in policy making and industrial research.
The industrial sector is one of the high energy consuming sectors in China, which determines that the industrial sector plays an important role in reducing energy consumption and environmental pollution. Chinese industrial energy consumption accounted for 65.6% of the country’s total energy consumption in 2017, according to data released by the National Bureau of Statistics. The huge consumption of industrial fossil energy will discharge a large amount of industrial wastewater, solid waste, and sulfur dioxide, which is one of the main culprits of smog. According to the China Environmental Statistics Yearbook, industrial wastewater emissions accounted for 27.1% of total wastewater emissions in 2015, and industrial sulfur dioxide emissions accounted for 83.7% of total sulfur dioxide emissions. The discharge of a large number of industrial pollutants is not only harmful to human health, but also detrimental to sustainable development strategies.
Industrial eco-efficiency is defined as the efficiency level of ecological resources to meet the needs of industrial development, aiming at the unification of economic efficiency and environmental benefits to achieve sustainable development of industrial economy and society. The concept of eco-efficiency was developed by the World Business Council for Sustainable Development. Eco-efficiency can be defined as the ratio of economic value to environmental impact [2]. It involves producing more goods and services with fewer resources, with less impact on the environment [3]. Eco-efficiency is defined as the ratio of environmental performance measurement index to financial performance measurement index. From this perspective, the goal is to achieve the lowest negative environmental impact with the lowest consumption of economic resources [4]. One of the basic characteristics of previous studies on the efficiency of industrial systems is that the industrial system is regarded as a “black box” structure, in which resources such as energy, capital, and labor are invested to obtain industrial emissions and GDP output without considering its internal structure, which often results in exaggerated efficiency results [5]. Because processes of industrial operations are often accompanied by a variety of undesirable industrial pollutants, these pollutants are an important goal of emission reduction. However, many different industrial pollutants are generated, and the process for reducing these is not the same; therefore, to ignore these different characteristics, inhibits accurate exploration of the eco-efficiency of the industrial system, and limits the ability to provide valuable information for energy conservation and emissions reduction targets. According to the characteristics of different links of production and pollution control in the industrial system, the Chinese provincial industrial system includes P stage, WWT stage, SWT stage, and SDT stage, and its structure is shown in Figure 1. In Figure 1, the P stage inputs energy, capital, and labor, producing industrial added value, wastewater, solid waste, and sulfur dioxide. Among them, wastewater, solid waste, and sulfur dioxide need to be treated through various treatment stages and then discharged. Wastewater treatment, solid waste treatment, and sulfur dioxide treatment all require additional investment in treatment. Wastewater and sulfur dioxide are treated and then discharged, while solid waste is treated by recycling and comprehensive utilization to reduce environmental pollution. Therefore, to improve the eco-efficiency of the entire industrial system, the efficiency of these four interrelated sub-stages must be improved simultaneously.
Figure 1. Network structure of industrial systems.

2.  Evaluating Efficiency of Industrial Based on Network DEA Method

At present, the concepts of energy conservation and emission reduction, clear water and green mountains have become more and more common across society. As one of the representative sectors of high energy consumption and high emissions, how to improve the energy and environmental efficiency of industrial enterprises has attracted more and more attention from the industry and academia. Generally speaking, the efficiency evaluation of industrial sectors is mainly carried out at the regional and industry levels. For example, reference [6] used a DEA based method to evaluate the energy and environmental efficiency of 30 regions in China and found that the energy and environmental efficiency of Chinese industry was poor. Reference [7] applied the Malmquist index (MI) method to evaluate the performance of industrial energy conservation and emission reduction in more than 200 Cities in China. Reference [8] used DEA to evaluate provincial environmental efficiency in China from 2004 to 2012. Reference [9] used the input-oriented ZSG-DEA model to explore the carbon emission quota efficiency of 39 industries in China in 2020.
There are two main methods to study the efficiency of industrial sectors. The first is parametric method represented by stochastic frontier method (SFA). For example, reference [10] used SFA to evaluate the GHG efficiency of 26 industries in China at the industry level and analyzed its influencing factors. Reference [11] proposed a hybrid method using logarithmic average divided by index, symmetric component, and SFA to estimate the energy saving potential of industrial sectors. Reference [12] quantitatively measured the total factor carbon emission performance and carbon emission reduction potential of 39 industrial sectors in the Beijing–Tianjin–Hebei region from 2010 to 2016 by using SFA method. However, a great limitation of these studies lies in the fact that the functional form of industrial production technology must be given compulsorily in advance, that is, a certain functional relationship between input and output, and different functional forms may lead to different evaluation results, which is a deficiency of SFA method for industrial system efficiency evaluation. The other is the more widely used non-parametric method represented by DEA, which makes up for the shortcomings of the SFA method. It does not need to specify a certain functional relationship between input and output. This method was first proposed by [13] in 1978. Since then, more and more research on methods, model innovation, and different application scenarios based on this method have been carried out, including [14][15]. For the research on energy and environment using DEA method, please refer to the review of [16].
Research on efficiency evaluation of industrial systems using traditional DEA or its extended model mostly regard the evaluated system as a “black box” structure without considering its internal situation. Reference [17] used the super-efficiency DEA model to evaluate the eco-environmental benefits of cities in the Yellow River Basin from 2008 to 2017, and discussed the temporal and spatial evolution characteristics of regional economic benefits and the factors affecting regional economic benefits. Reference [18] used the data of 42 thermal power plants in China in 2020 to construct a multi-dimensional index evaluation system of carbon emission efficiency from three aspects: energy, economy, and environment. The super-efficiency slacks-based measure (SBM) model with undesirable output is used to identify and distinguish several efficient decision units and the efficiency improvement path of inefficient thermal power plant is discussed. Reference [19] used non-parametric DEA and fractional regression model to analyze the evolution of eco-efficiency in 27 countries of the European Union (EU) from 2008 to 2018, providing a high level of attention to the relationship between economic growth and environmental performance in the EU. Reference [20] extends the previous framework for efficiency analysis, introducing a new slacks-based measure of efficiency called the scale directional distance function (SDDF) approach, used to measure the eco-efficiency of Malaysia’s manufacturing industry. Reference [21] uses DEA methodology to calculate environmental efficiency across the 28 member states of the European Union (EU). For more studies in this field, please refer to [22][23][24][25][26][27][28]. To determine the causes of inefficiency in industrial systems, it is necessary to consider the internal structure of industrial systems. Therefore, reference [29] developed a network DEA model for evaluating organizational performance and its component performance. The proposed network DEA model has aroused the research interest of many scholars, and many new network DEA expansion models have been developed successively, such as network SBM model and dynamic network SBM model of [30][31], additive network DEA efficiency decomposition model of [32], and network DEA efficiency decomposition method of [33]. Reference [34] extended the traditional two-stage network DEA model to the uncertain two-stage network DEA model. Reference [35] proposed a common weight network DEA model when the production system contains multiple interrelated processes. The two-stage DEA model is a kind of network model. Reference [36] used two-stage DEA model to construct an index system to measure the mining technology innovation efficiency, mining eco-efficiency, and mining comprehensive efficiency of 30 provinces in China. Reference [37] simulated the operation process of the electric power industry through the network structure, introduced the dynamic slacks-based measure method, and evaluated the operation efficiency of the whole industry and each stage in each period. Reference [38] proposed a two-stage efficiency evaluation model of Chinese regional industrial system based on SBM-DEA. The model decomposed efficiency into production efficiency and emission reduction efficiency, which can simultaneously estimate the efficiency of the entire regional industrial system, production stage, and emission reduction stage. However, this study did not consider the differences in the treatment processes of different industrial pollutants in the treatment stage, and could not further find out the cause of low efficiency in the internal stage of the system. Reference [39] separated the energy production sector from the energy consumption sector and proposed an adjusted energy efficiency evaluation network DEA model, which was then applied to the energy efficiency evaluation of provincial industrial sectors in China. Reference [40] established a network SBM model to evaluate the environmental performance of the Chinese industrial system. Reference [41] proposed a two-stage game DEA method, using centralized and Stackelberg game models to measure the cost efficiency (CE) of Iran’s power grid. Reference [42] extended the existing two-stage network DEA model that distinguishes pure energy efficiency from economic efficiency to investigate whether energy efficiency has a positive relationship with corporate financial performance in South Korea. Reference [43] used a dynamic network DEA (DNDEA) model to evaluate the performance of Taiwan’s machine tool industry from 2010 to 2014. Using data from fiscal 2011 and 2017, reference [44] analyzed the efficiency of the Italian urban water sector using an extended parallel network DEA model. These studies considered the internal structure of the industrial system, but did not carry out a further analysis of the sub-stage, so they could not further find out the deeper reasons for the inefficiency of the system. In view of this, researchers proposes a new network SBM model according to the characteristics of the system structure, and evaluates the efficiency of the Chinese provincial industrial system. The research route is shown in Figure 2.
Figure 2. The research flow chart.

References

  1. Zhang, L.; Zhao, L.L.; Zha, Y. Efficiency evaluation of Chinese regional industrial systems using a dynamic two-stage DEA approach. Socio-Econ. Plan. Sci 2021, 77, 101031.
  2. Díaz-Villavicencio, G.; Didonet, S.R.; Dodd, A. Influencing factors of eco-efficient urban waste management: Evidence from Spanish municipalities. J. Clean. Prod. 2017, 164, 1486–1496.
  3. Delgado-Antequera, L.; Gémar, G.; Molinos-Senante, M.; Gómez, T.; Caballero, R.; Sala-Garrido, R. Eco-efficiency assessment of municipal solid waste services: Influence of exogenous variables. Waste Manag. 2021, 130, 136–146.
  4. Lo Storto, C. Eco-Productivity Analysis of the Municipal Solid Waste Service in the Apulia Region from 2010 to 2017. Sustainability 2021, 13, 12008.
  5. Li, R.; Sun, T. Research on Impact of Different Environmental Regulation Tools on Energy Efficiency in China. Pol. J. Environ. Stud. 2020, 29, 4151–4160.
  6. Wu, J.; Zhu, Q.; Liang, L. CO2 emissions and energy intensity reduction allocation over provincial industrial sectors in China. Appl. Energy 2016, 166, 282–291.
  7. Zhou, D.Q.; Wang, Q.; Su, B.; Zhou, P.; Yao, L.X. Industrial energy conservation and emission reduction performance in China: A city-level nonparametric analysis. Appl. Energy 2016, 166, 201–209.
  8. Song, M.L.; Peng, J.; Wang, J.L.; Zhao, J.J. Environmental efficiency and economic growth of China: A Ray slack-based model analysis. Eur. J. Oper. Res. 2018, 269, 51–63.
  9. Zhang, Y.-J.; Hao, J.-F. Carbon emission quota allocation among China’s industrial sectors based on the equity and efficiency principles. Ann. Oper. Res. 2016, 255, 117–140.
  10. Sun, J.; Du, T.; Sun, W.; Na, H.; He, J.; Qiu, Z.; Yuan, Y.; Li, Y. An evaluation of greenhouse gas emission efficiency in China’s industry based on SFA. Sci. Total Environ. 2019, 690, 1190–1202.
  11. Fetanat, A.; Shafipour, G. A hybrid method of LMDI, symmetrical components, and SFA to estimate the distribution of energy-saving potential with consideration of unbalanced components in decomposition analysis. Energ Effic. 2017, 10, 1041–1059.
  12. Wang, C.; Zhan, J.; Bai, Y.; Chu, X.; Zhang, F. Measuring carbon emission performance of industrial sectors in the Beijing-Tianjin-Hebei region, China: A stochastic frontier approach. Sci. Total Environ. 2019, 685, 786–794.
  13. Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444.
  14. Chen, L.; Jia, G. Environmental efficiency analysis of China’s regional industry: A data envelopment analysis (DEA) based approach. J. Clean. Prod. 2017, 142, 846–853.
  15. Zhou, H.; Yang, Y.; Chen, Y.; Zhu, J. Data envelopment analysis application in sustainability: The origins, development and future directions. Eur. J. Oper. Res. 2018, 264, 1–16.
  16. Sueyoshi, T.; Yuan, Y.; Goto, M. A literature study for DEA applied to energy and environment. Energy Econ. 2017, 62, 104–124.
  17. Song, C.; Yin, G.; Lu, Z.; Chen, Y. Industrial ecological efficiency of cities in the Yellow River Basin in the background of China’s economic transformation: Spatial-temporal characteristics and influencing factors. Environ. Sci. Pollut. Res. Int. 2022, 29, 4334–4349.
  18. Fang, T.; Fang, D.; Yu, B. Carbon emission efficiency of thermal power generation in China: Empirical evidence from the micro-perspective of power plants. Energ Policy 2022, 165, 112955.
  19. Moutinho, V.; Madaleno, M. A Two-Stage DEA Model to Evaluate the Technical Eco-Efficiency Indicator in the EU Countries. Int. J. Environ. Res. Public Health 2021, 18, 3038.
  20. Ramli, N.A.; Munisamy, S.; Arabi, B. Scale directional distance function and its application to the measurement of eco-efficiency in the manufacturing sector. Ann. Oper. Res. 2013, 211, 381–398.
  21. Hermoso-Orzáez, M.J.; García-Alguacil, M.; Terrados-Cepeda, J.; Brito, P. Measurement of Environmental Efficiency in the Countries of the European Union with the Enhanced Data Envelopment Analysis Method (DEA) during the Period 2005–2012. In Proceedings of the 5th Ibero-American Congress on Entrepreneurship, Energy, Environment and Technology—CIEEMAT, Portalegre, Portugal, 11–13 September 2019.
  22. Wang, K.; Wei, Y.-M. China’s regional industrial energy efficiency and carbon emissions abatement costs. Appl. Energy 2014, 130, 617–631.
  23. Nguyen, N.T. Integrating two stages of Malmquist index and Grey forecasting to access industrial performance: A case of Vietnamese steel industry. J. Grey Syst. 2021, 33, 43–58.
  24. Bi, G.-B.; Song, W.; Zhou, P.; Liang, L. Does environmental regulation affect energy efficiency in China’s thermal power generation? Empirical evidence from a slacks-based DEA model. Energ Policy 2014, 66, 537–546.
  25. Guo, X.; Zhu, Q.; Lv, L.; Chu, J.; Wu, J. Efficiency evaluation of regional energy saving and emission reduction in China: A modified slacks-based measure approach. J. Clean. Prod. 2017, 140, 1313–1321.
  26. Sueyoshi, T.; Goto, M. Undesirable congestion under natural disposability and desirable congestion under managerial disposability in U.S. electric power industry measured by DEA environmental assessment. Energy Econ. 2016, 55, 173–188.
  27. Zhu, N.; He, K. The efficiency of major industrial enterprises in Sichuan province of China: A super slacks-based measure analysis. J. Ind. Manag. Optim. 2022.
  28. Wu, J.; Li, M.J.; Zhu, Q.Y.; Zhou, Z.X.; Liang, L. Energy and environmental efficiency measurement of China’s industrial sectors: A DEA model with non-homogeneous inputs and outputs. Energy Econ. 2019, 78, 468–480.
  29. Färe, R.; Grosskopf, S. Network DEA. Socio-Econ. Plan. Sci. 2000, 34, 35–49.
  30. Tone, K.; Tsutsui, M. Network DEA: A slacks-based measure approach. Eur. J. Oper. Res. 2009, 197, 243–252.
  31. Tone, K.; Tsutsui, M. Dynamic DEA with network structure: A slacks-based measure approach. Omega-Int. J. Manag. Sci. 2014, 42, 124–131.
  32. Cook, W.D.; Zhu, J.; Bi, G.B.; Yang, F. Network DEA: Additive efficiency decomposition. Eur. J. Oper. Res. 2010, 207, 1122–1129.
  33. Kao, C. Decomposition of slacks-based efficiency measures in network data envelopment analysis. Eur. J. Oper. Res. 2020, 283, 588–600.
  34. Jiang, B.; Chen, H.; Li, J.; Lio, W.C. The uncertain two-stage network DEA models. Soft Comput. 2020, 25, 421–429.
  35. Hatami-Marbini, A.; Saati, S. Measuring performance with common weights: Network DEA. Neural Comput. Appl. 2020, 32, 3599–3617.
  36. Zuo, Z.; Guo, H.; Li, Y.; Cheng, J. A two-stage DEA evaluation of Chinese mining industry technological innovation efficiency and eco-efficiency. Environ. Impact Assess. Rev. 2022, 94, 106762.
  37. Meng, M.; Pang, T. Operational efficiency analysis of China’s electric power industry using a dynamic network slack-based measure model. Energy 2022, 251, 123898.
  38. Bian, Y.; Liang, N.; Xu, H. Efficiency evaluation of Chinese regional industrial systems with undesirable factors using a two-stage slacks-based measure approach. J. Clean. Prod. 2015, 87, 348–356.
  39. Liu, Y.; Wang, K. Energy efficiency of China’s industry sector: An adjusted network DEA (data envelopment analysis)-based decomposition analysis. Energy 2015, 93, 1328–1337.
  40. Li, Y.J.; Shi, X.; Emrouznejad, A.; Liang, L. Environmental performance evaluation of Chinese industrial systems: A network SBM approach. J. Oper. Res. Soc. 2018, 69, 825–839.
  41. Mousavizadeh, R.; Navabakhsh, M.; Hafezalkotob, A. Cost-efficiency measurement for two-stage DEA network using game approach: An application to electrical network in Iran. Sadhana-Acad. Proc. Eng. Sci. 2020, 45, 1–16.
  42. Moon, H.; Min, D. A DEA approach for evaluating the relationship between energy efficiency and financial performance for energy-intensive firms in Korea. J. Clean. Prod. 2020, 255, 120283.
  43. Lu, C.C.; Dan, W.; Chen, X.; Tseng, C.K.; Chou, K.W. Evaluation of the operating performance of Taiwanese machine tool industry with the dynamic network DEA model. Enterp. Inf. Syst. 2020, 15, 87–104.
  44. Lo Storto, C. Measuring the efficiency of the urban integrated water service by parallel network DEA: The case of Italy. J. Clean. Prod. 2020, 276.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Mathematics, Applied
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Kai He
,
Nan Zhu
,
Jiang Wu
,
Chuanjin Zhu
View Times: 773
Revisions: 2 times (View History)
Update Date: 24 May 2022
Table of Contents
    1000/1000
    Hot Most Recent
    Feedback