Your browser does not fully support modern features. Please upgrade for a smoother experience.

Submitted Successfully!
Thank you for your contribution! You can also upload a video entry or images related to this topic.
For video creation, please contact our Academic Video Service.
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Jian Fu Zhang | -- | 3283 | 2022-05-13 09:30:55 | | | |
| 2 | Camila Xu | -5 word(s) | 3278 | 2022-05-13 11:00:52 | | |
Video Upload Options
We provide professional Academic Video Service to translate complex research into visually appealing presentations. Would you like to try it?
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Zhang, J.F.; , .; Duan, M. Bias Temperature Instability of MOSFETs. Encyclopedia. Available online: https://encyclopedia.pub/entry/22906 (accessed on 08 January 2026).
Zhang JF, , Duan M. Bias Temperature Instability of MOSFETs. Encyclopedia. Available at: https://encyclopedia.pub/entry/22906. Accessed January 08, 2026.
Zhang, Jian Fu, , Meng Duan. "Bias Temperature Instability of MOSFETs" Encyclopedia, https://encyclopedia.pub/entry/22906 (accessed January 08, 2026).
Zhang, J.F., , ., & Duan, M. (2022, May 13). Bias Temperature Instability of MOSFETs. In Encyclopedia. https://encyclopedia.pub/entry/22906
Zhang, Jian Fu, et al. "Bias Temperature Instability of MOSFETs." Encyclopedia. Web. 13 May, 2022.
Copy Citation
CMOS technology dominates the semiconductor industry, and the reliability of MOSFETs is a key issue. Negative bias temperature instability (NBTI) and positive bias temperature instability (PBTI) mainly degrade the performance of pMOSFETs and nMOSFETs, respectively.
reliability
instability
aging
degradation
bias temperature instability (BTI)
1. Introduction
Failures of electronic products have been commonly encountered in our daily life, and there is no way that a product can be made with a zero failure rate. Different products require different levels of reliability. For example, the failure rate in auto-electronic components must be lower than that in electronic toys. Failure can be broadly divided into two types: permanent breakdown and temporary malfunction, where a product can recover by, for example, restarting it. Failure rate can be improved by sacrificing performance such as speed and power consumption. A successful commercial product should have a well-balanced trade-off between the failure rate, performance, and costs.
Ever since CMOS was invented in 1963, its reliability has always been a key issue [1][2][3][4][5][6][7][8][9][10][11][12][13][14][15][16][17][18][19][20][21][22][23][24][25][26][27][28][29][30][31][32][33][34][35][36][37][38][39]. Failure occurs at both the frontend [1][2][3][4], where MOSFETs are located, and the backend [5][6]. The backend includes multiple metal layers for connections and low-k dielectrics between these layers. The metal wires suffer from electromigration [5], where metal atoms gradually migrate from their initial locations, eventually resulting in open or short circuits. To minimize time delay, the dielectric between these metal wires must have low dielectric constants, making them vulnerable to both mechanical and electrical breakdown [6].
There are different types of instability for MOSFETs at the frontend including mobile ions [7], hot carriers [8][9], time-dependent dielectric breakdown (TDDB) [10], bias temperature instabilities (BTIs) [1][2][3][4], and random telegraph noise (RTN) [11][12][13]. Their relative importance changes with time. To show this change, researchers named one type as the dominant instability for each decade after the invention of CMOS in Figure 1. In the 1960s and 1970s, mobile ions in gate oxide, such as sodium ions (Na+), were a major concern [7]. They originate from contamination and have been effectively eliminated by using cleanroom technologies.
 Figure 1. The main reliability issue in each decade for CMOS technologies. DDV: device-to-device variation.
Figure 1. The main reliability issue in each decade for CMOS technologies. DDV: device-to-device variation.In 1980s, the operation voltage was kept at 5 V when device sizes were downscaled as shown in Figure 2. This leads to an increase in the electrical field, which accelerates charge carriers in the conduction channel and makes them “hot”. Through impact and ionization, hot carriers can cause damage to devices by generating interface states and forming space charges in gate oxides, which reduce the driving current, Id, under a given bias [8][9]. A typical definition for device lifetime is the time for an Id reduction of 10% [8][9], and hot-carrier-induced aging limited device lifetime in the 1980s.
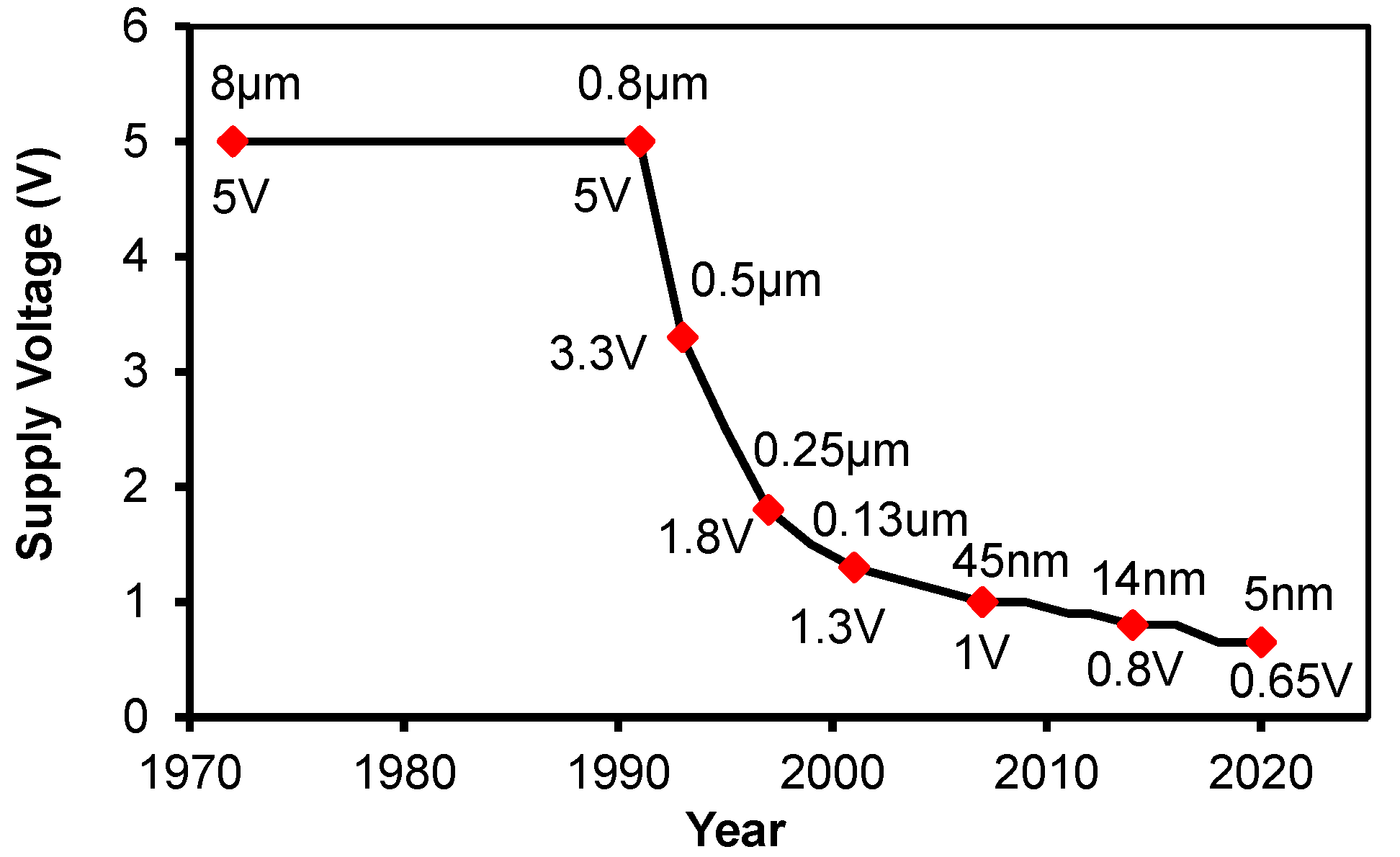 Figure 2. The supply voltage of different generations of CMOS technologies. It was fixed at 5 V before 1990s but has been reduced with the downscaling of device sizes since 1990.
Figure 2. The supply voltage of different generations of CMOS technologies. It was fixed at 5 V before 1990s but has been reduced with the downscaling of device sizes since 1990.In 1990s, the continuous reduction in the operation voltage, as shown in Figure 2, reduced the relative importance of hot carrier aging. Gate oxides became sufficiently thin, and direct tunneling occurred through them. This causes damage to gate oxides. The damage accumulates and eventually triggers oxide breakdown. As the damage accumulation takes some time, the breakdown is referred to as time-dependent dielectric breakdown (TDDB). TDDB was the dominant reliability issue in the 1990s [10].
In 2000s, negative bias temperature instability (NBTI) of pMOSFETs became the lifetime-limiting instability and attracted much attention [14][15][16][17][18][19][20][21][22]. The difference between hot carrier aging (HCA) and NBTI is that HCA occurs mainly near the drain junction, while NBTI happens uniformly. Before high-k dielectrics were used, silicon dioxides were nitrided to form oxynitrides, which increases NBTI [14]. BTI was also a major barrier to overcome in developing high-k processes [23][24][25].
Since 2010s, devices have become so small that device-to-device variations (DDVs) are a major challenge to circuit design. In addition to the static as-fabricated DDVs [26], device aging is stochastic and introduces time-dependent variation (TDV) [27][28][29][30][31]. Both HCA and BTI contribute to TDV. Moreover, for nanoscale devices, a single trap in the gate dielectric can capture a carrier from the conduction channel and induce considerable change of Id in the form of random telegraph noise (RTN) [11][12][13]. RTN is different from aging: aging shifts device parameters in one direction, while RTN causes their fluctuation in both directions. This further complicates the characterization and modeling of TDV.
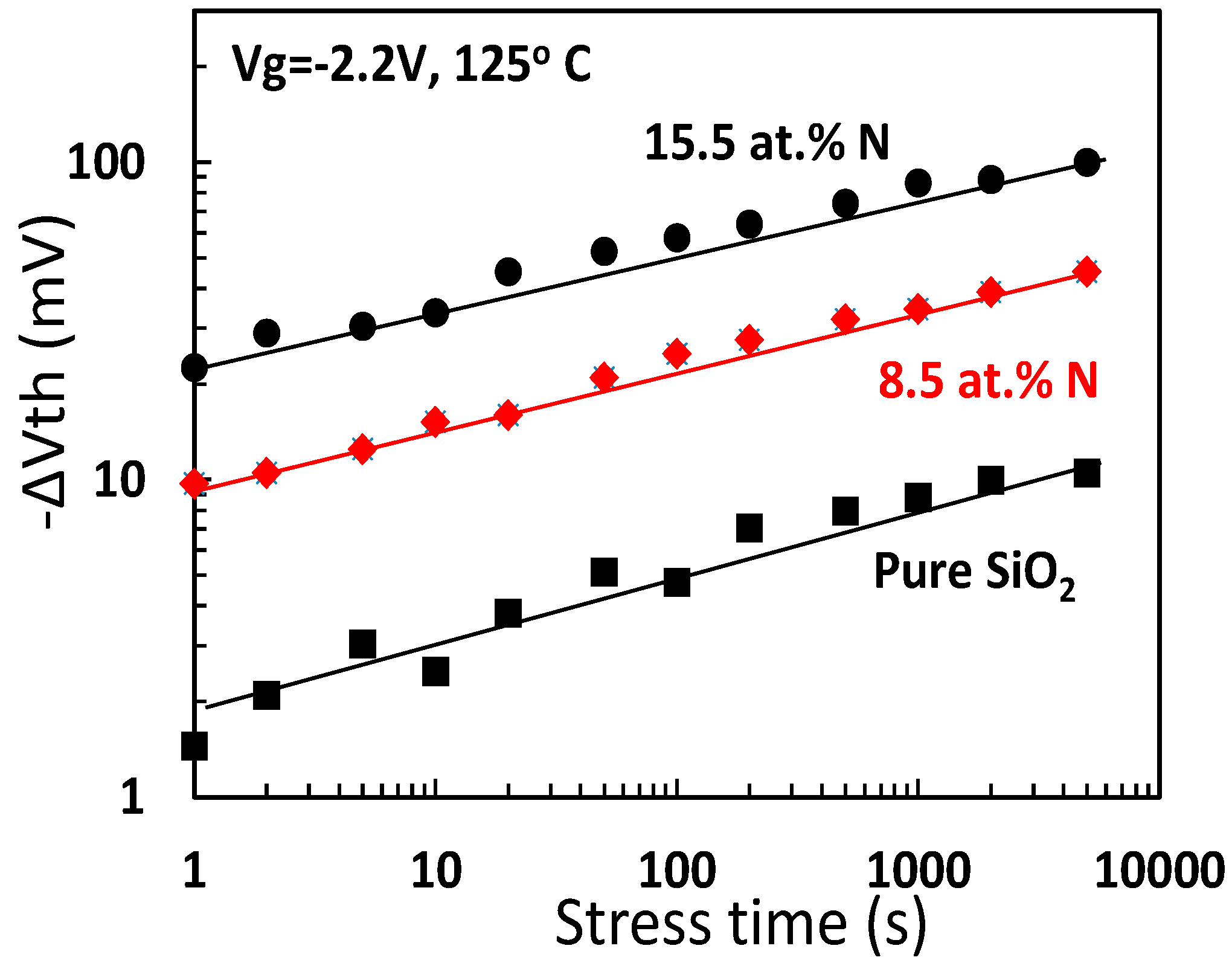 Figure 4. Increase of nitrogen density in SiON raises NBTI. The NBTI follows a power law [14].
Figure 4. Increase of nitrogen density in SiON raises NBTI. The NBTI follows a power law [14].
2. Negative Bias Temperature Instability (NBTI)
NBTI and PBTI mainly degrade the performance of pMOSFETs and nMOSFETs, respectively. Early attention was focused on NBTI, as it is generally higher than PBTI and limits the lifetime of pMOSFETs.
2.1. Pre-2000 NBTI
NBTI was reported only a few years after the invention of CMOS technology and is one of the earliest instabilities observed for MOSFETs [1]. Under a negative gate bias, positive charges build up both in the gate oxide and from the generated interface states as shown in Figure 3a. This results in a negative shift in the capacitance–voltage (CV) characteristics, as shown in Figure 3b [1], and an increase in the magnitude of the threshold voltage of pMOSFETs [17].
Before 2000, the gate oxide used to study NBTI was relatively thick (e.g., >4 nm) and the oxide field applied was generally too low for electrons to tunnel through the oxide [1][2][3]. These NBTI works are hereafter referred to as “pre-2000 NBTI”. Under these conditions, NBTI has the following features:
-
Figure 4 shows that NBTI follows power law against stress time. The power exponent is insensitive to gate bias and temperature [14];
-
Its recovery is insignificant;
-
It also follows power law against gate bias;
-
It is thermally activated.
 Figure 4. Increase of nitrogen density in SiON raises NBTI. The NBTI follows a power law [14].
Figure 4. Increase of nitrogen density in SiON raises NBTI. The NBTI follows a power law [14].On the physical process, the Si–H bond at the interface is generally believed to be the precursor for generated interface states [17]. During NBTI stress, Si–H is ruptured, and the released hydrogenous species then migrate into the gate oxide, leaving behind the Si dangling bond, also commonly known as the Pb-center, as the interface state [2][4][17]. The generated interface states in the lower half of Si bandgap are donor-like. As gate bias is swept in the negative direction, there are an increasing amount of them moving above the Fermi-level at the interface, Ef, and becoming positively charged. This leads to the nonparallel shift in CV as shown in Figure 3b.
In addition to the nonparallel shift, there is also a parallel negative shift, as shown in Figure 3b, which is caused by positive charges formed in the oxide. The magnitude of parallel shift is similar to that of nonparallel shift in Figure 3b, indicating a one-to-one correlation between the oxide charges and the positive charges from the generated interface states. This, however, does not mean that the oxide charge density is equal to the density of the generated interface states. As each Pb-center has two states, one acceptor-like in the upper-half of Si bandgap and one donor-like in the lower half of bandgap, the interface state density measured using a popular technique, such as charge pumping, should double the oxide charge density.
On the aging kinetics, it was proposed that the power law results from the diffusion of hydrogenous species through gate oxides as the rate limiting process [2][4]. This hypothesis was challenged as the gate oxide of modern MOSFETs is too thin and the time for hydrogenous species diffusing through it is too short to limit the aging process [17].
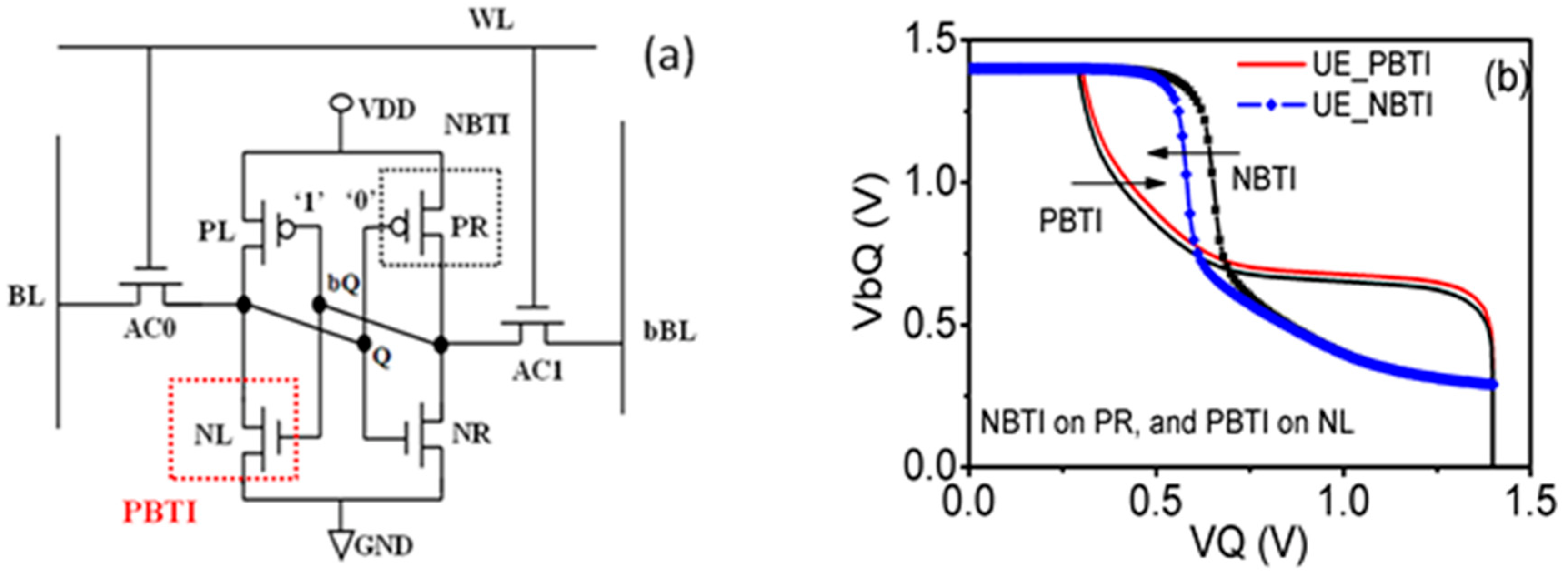 Figure 5. (a) When a SRAM cell holds a data bit, PBTI occurs in one of the pull-down nMOSFETs, while NBTI happens in the pull-up pMOSFET of the opposite inverters; (b) both PBTI and NBTI contribute to the reduction in the static noise margin (i.e., the size of butterfly eyes) by making the two inverters imbalance [29].
Figure 5. (a) When a SRAM cell holds a data bit, PBTI occurs in one of the pull-down nMOSFETs, while NBTI happens in the pull-up pMOSFET of the opposite inverters; (b) both PBTI and NBTI contribute to the reduction in the static noise margin (i.e., the size of butterfly eyes) by making the two inverters imbalance [29].
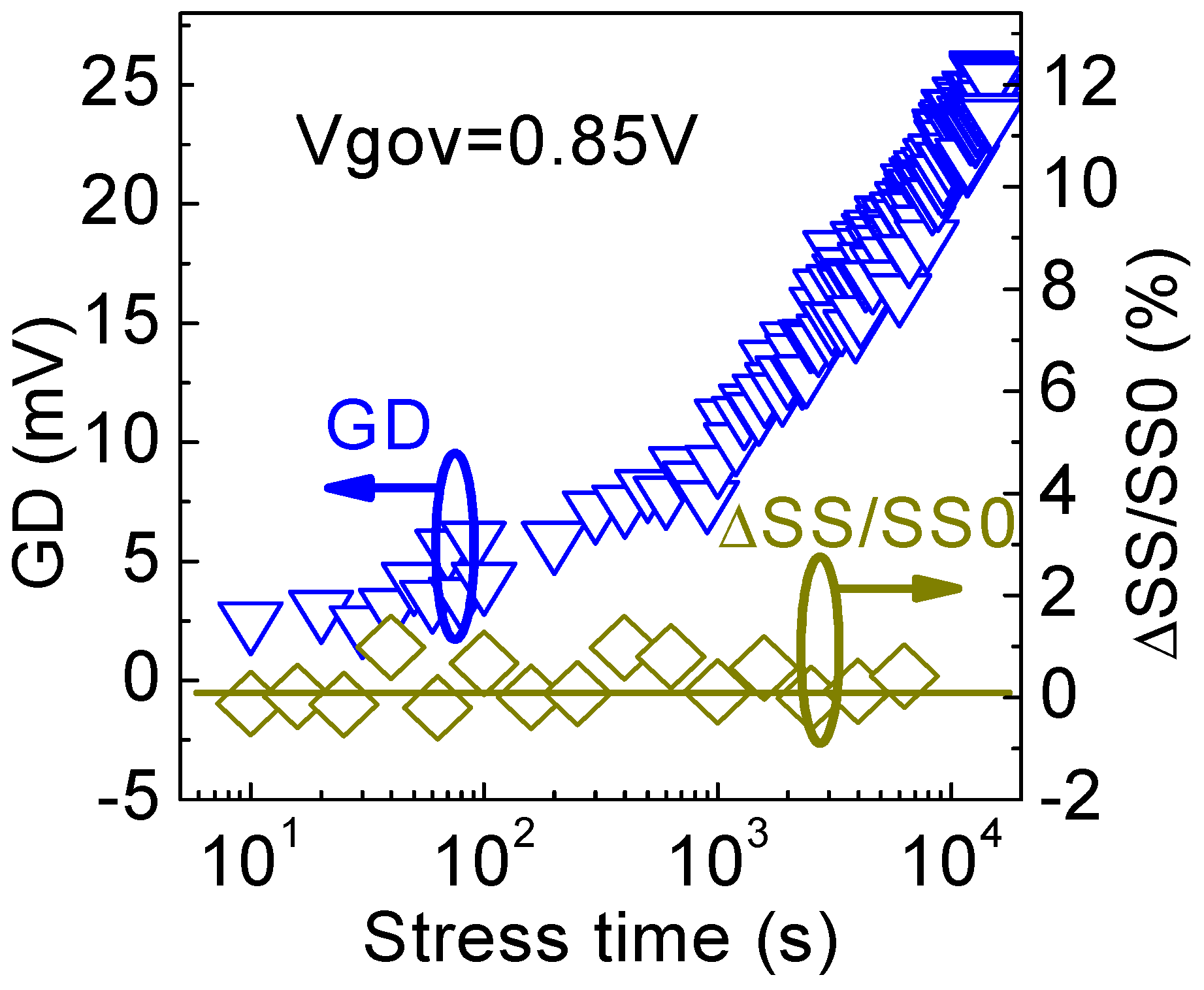 Figure 6. Under positive gate bias, generated defects (GDs) increased, but the negligible change in subthreshold swing (SS) indicates that interface states were not created [39].
Figure 6. Under positive gate bias, generated defects (GDs) increased, but the negligible change in subthreshold swing (SS) indicates that interface states were not created [39].
 Figure 7. There are little as-grown electron traps in the poly-Si-gated SiO2 [46].
Figure 7. There are little as-grown electron traps in the poly-Si-gated SiO2 [46].
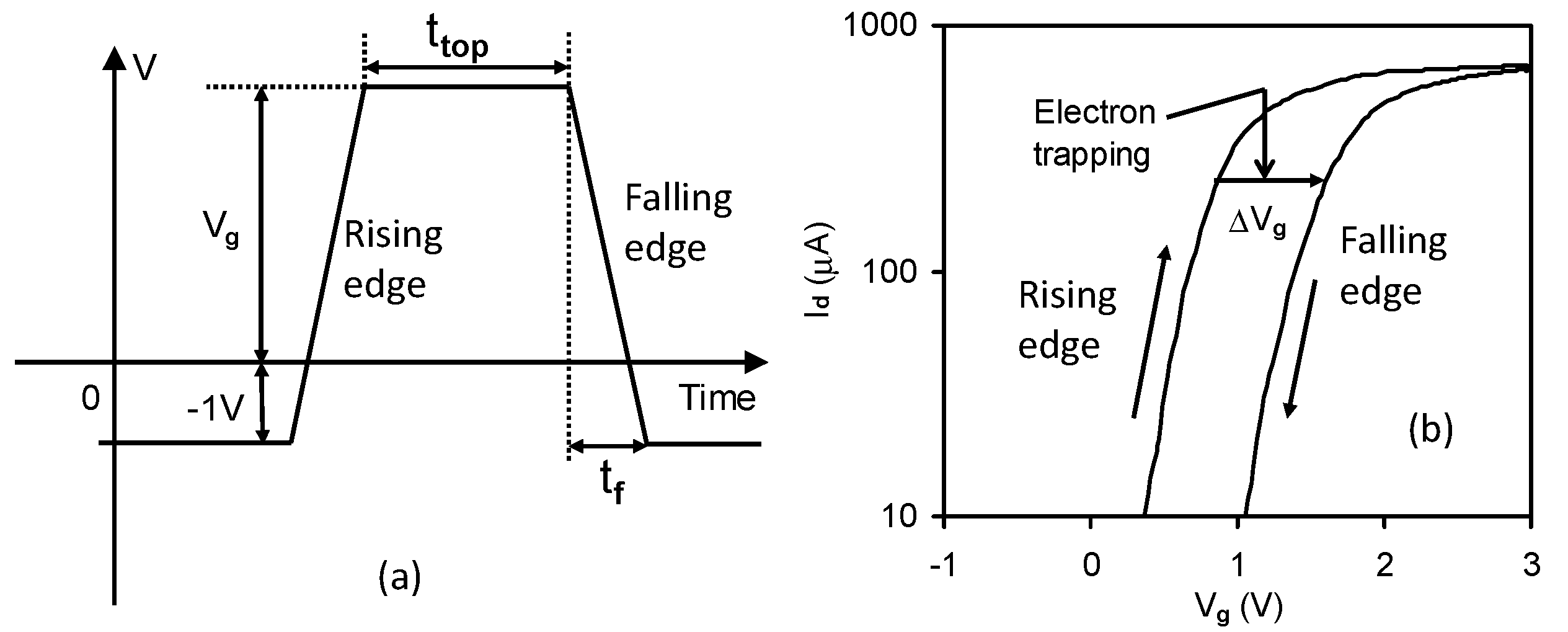 Figure 8. (a) The gate bias waveform; (b) the pulse Id-Vg recorded at the rising and falling edges of the gate bias [25].
Figure 8. (a) The gate bias waveform; (b) the pulse Id-Vg recorded at the rising and falling edges of the gate bias [25].
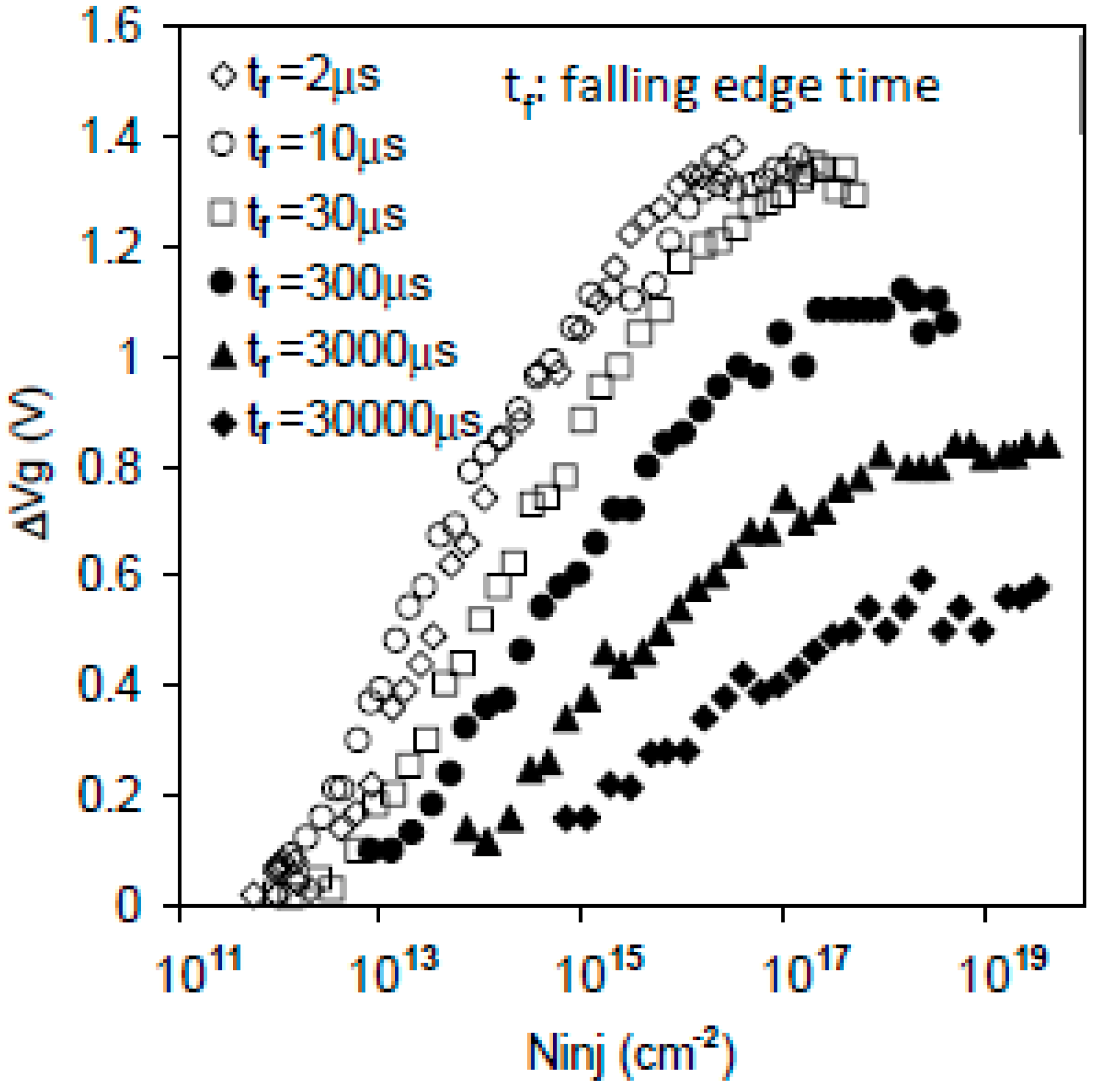 Figure 9. An increase in the falling edge time resulted in a lower trapping level because the trapped electrons can be detrapped before the measurement [47].
Figure 9. An increase in the falling edge time resulted in a lower trapping level because the trapped electrons can be detrapped before the measurement [47].
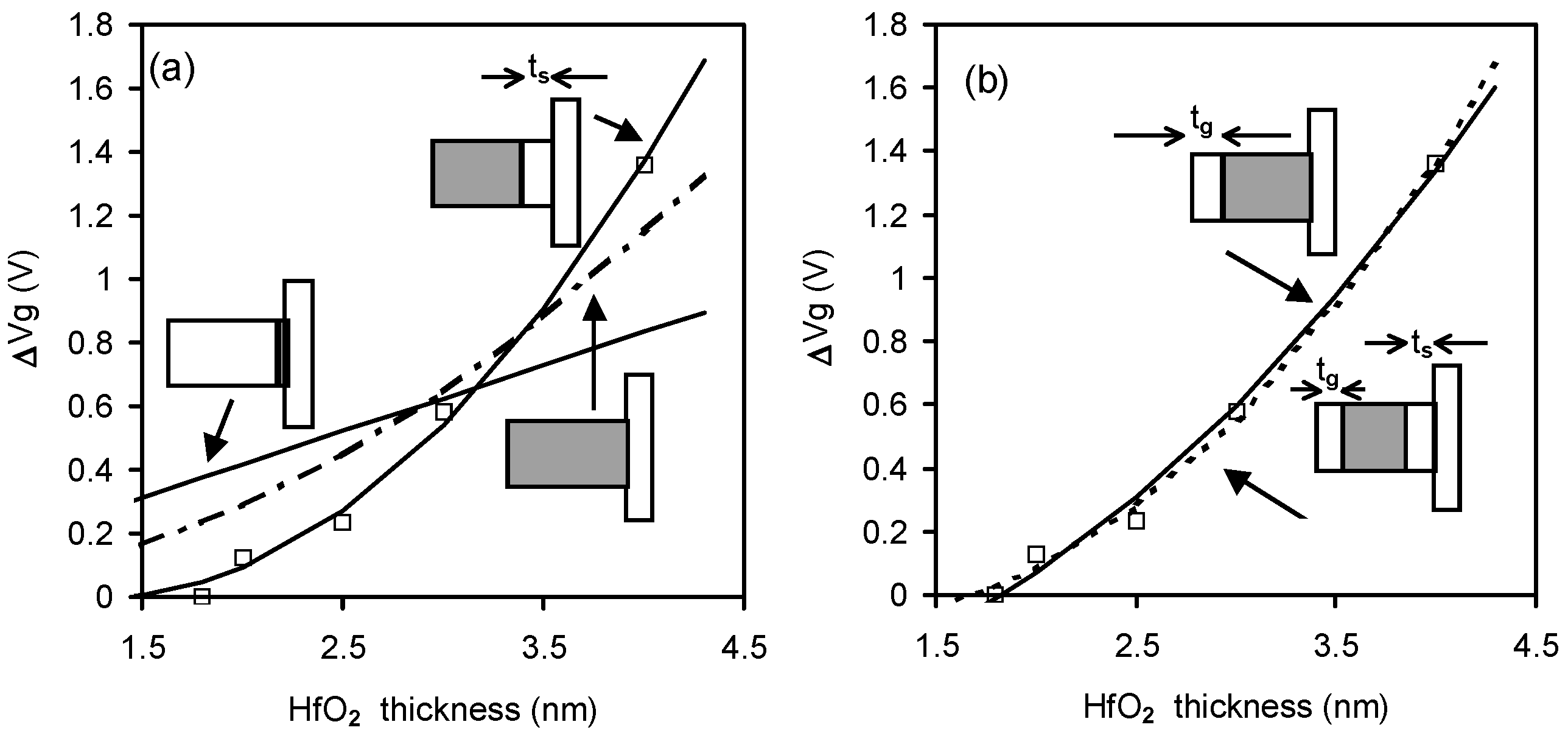 Figure 10. The location of as-grown electron traps in HfO2. Symbols represent the test data, and the lines are fitted with traps located in the grey regions [47].
Figure 10. The location of as-grown electron traps in HfO2. Symbols represent the test data, and the lines are fitted with traps located in the grey regions [47].
 Figure 11. The rapid reduction of as-grown electron trapping with the downscaling of the thickness of HfO2 [47].
Figure 11. The rapid reduction of as-grown electron trapping with the downscaling of the thickness of HfO2 [47].
 Figure 12. A comparison of PBTI with NBTI during stress (a) and recovery (b). (a) Shows that the PBTI was similar to NBTI during stress for this CMOS process but more stable during recovery [9].
Figure 12. A comparison of PBTI with NBTI during stress (a) and recovery (b). (a) Shows that the PBTI was similar to NBTI during stress for this CMOS process but more stable during recovery [9].
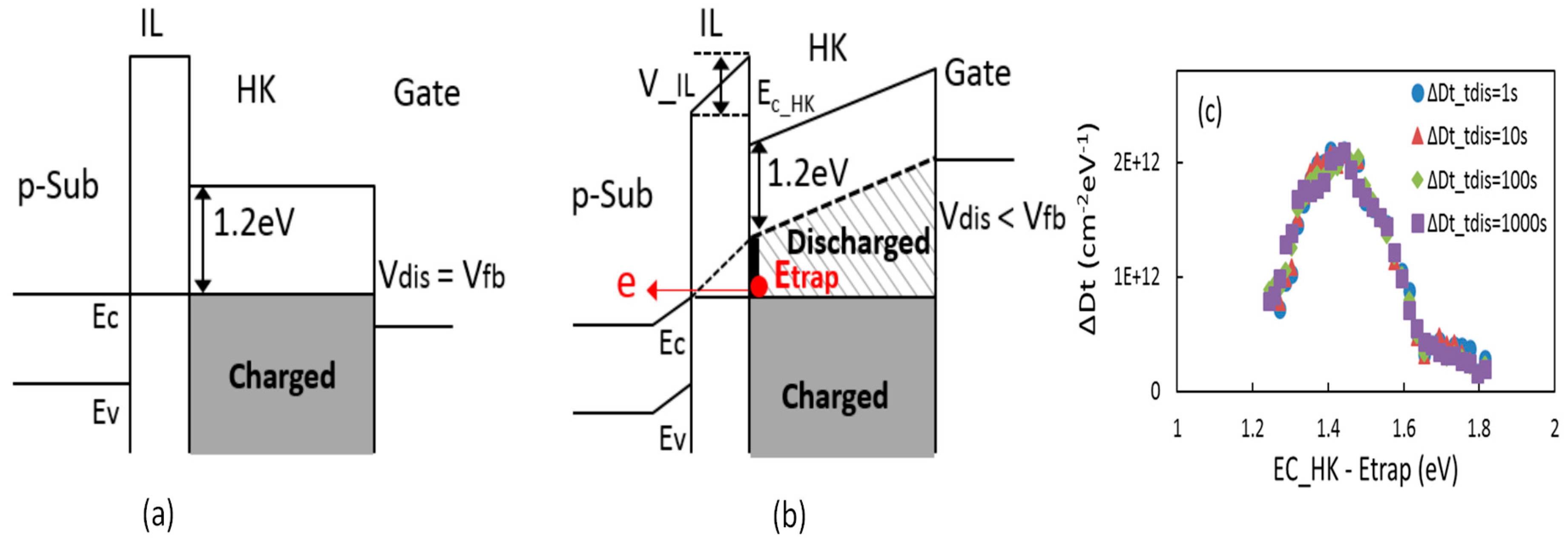 Figure 13. Probing the energy distribution profile of electron traps: (a) the electron traps below Si Ec were first charged; (b) applying a positive Vg will lift some charged traps above Ec for discharging, i.e., the striped region; (c) the extracted energy profile of electron traps by progressively increasing Vg for discharging [48].
Figure 13. Probing the energy distribution profile of electron traps: (a) the electron traps below Si Ec were first charged; (b) applying a positive Vg will lift some charged traps above Ec for discharging, i.e., the striped region; (c) the extracted energy profile of electron traps by progressively increasing Vg for discharging [48].
 Figure 14. (a) Test sequence for confirming the presence of as-grown defects and the generated Anti-neutralization electron traps (ANETs) by PBTI; (b) a comparison of the as-grown defects pre- and post-heavy PBTI stress [48].
Figure 14. (a) Test sequence for confirming the presence of as-grown defects and the generated Anti-neutralization electron traps (ANETs) by PBTI; (b) a comparison of the as-grown defects pre- and post-heavy PBTI stress [48].
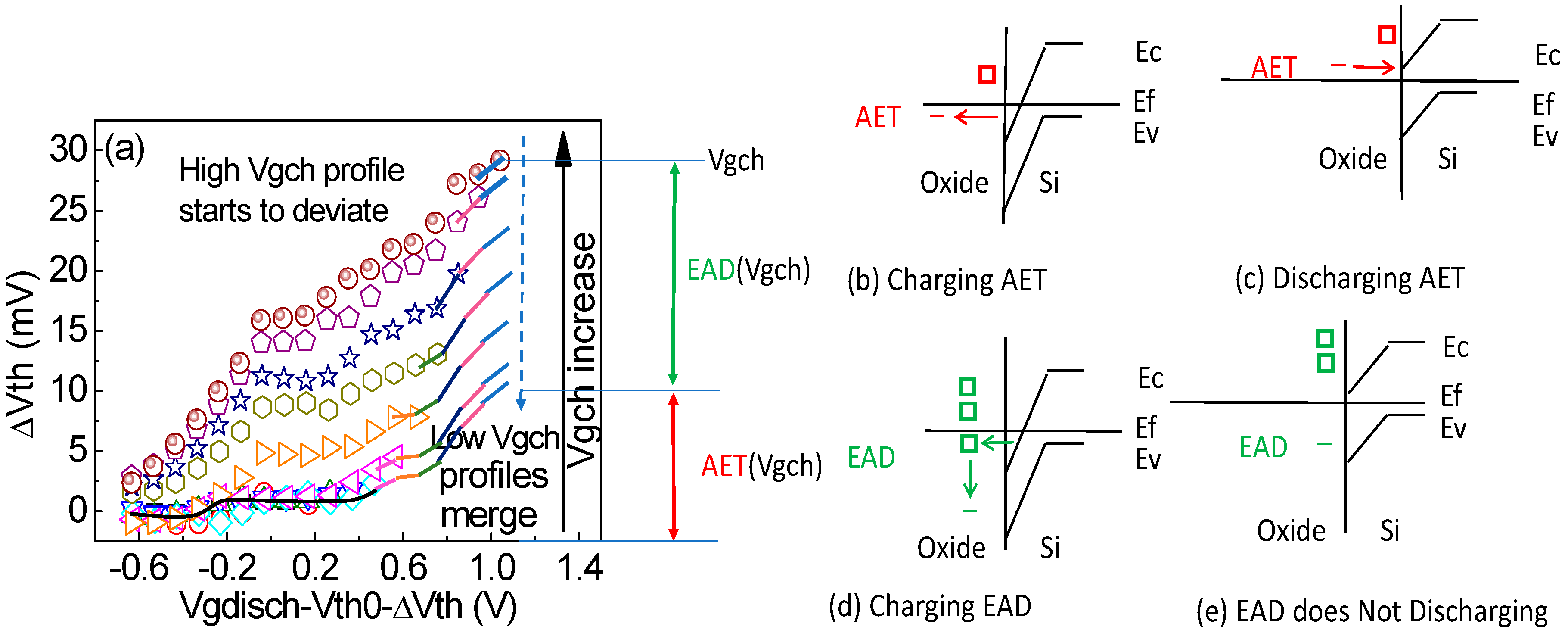 Figure 15. (a) Tests for separating as-grown electron traps (AETs) from the as-grown energy-alternating defects (EADs) [39]. (b) When an AET is below Ef, it is charged. (c) The energy levels of the AETs did not change after charging. It was discharged when above the same Ef for its charging. (d) When an EAD is below Ef, it is charged. After charging, the energy level of the EAD is lowered, so that it will not be discharged under the same Ef for its charging in (e).
Figure 15. (a) Tests for separating as-grown electron traps (AETs) from the as-grown energy-alternating defects (EADs) [39]. (b) When an AET is below Ef, it is charged. (c) The energy levels of the AETs did not change after charging. It was discharged when above the same Ef for its charging. (d) When an EAD is below Ef, it is charged. After charging, the energy level of the EAD is lowered, so that it will not be discharged under the same Ef for its charging in (e).
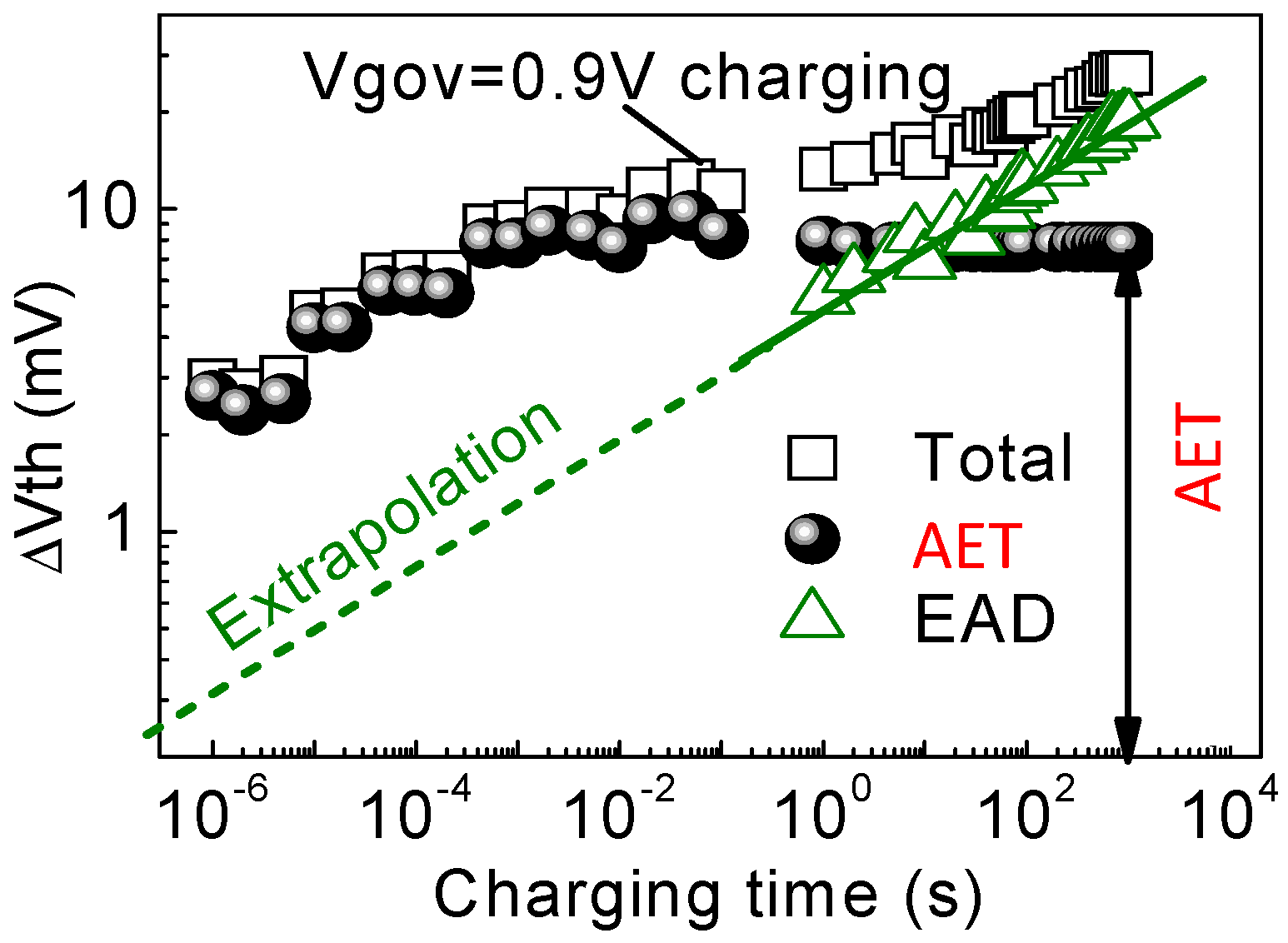 Figure 16. Extracting the kinetics of an EAD and an AET from the measured total ΔVth [39].
Figure 16. Extracting the kinetics of an EAD and an AET from the measured total ΔVth [39].
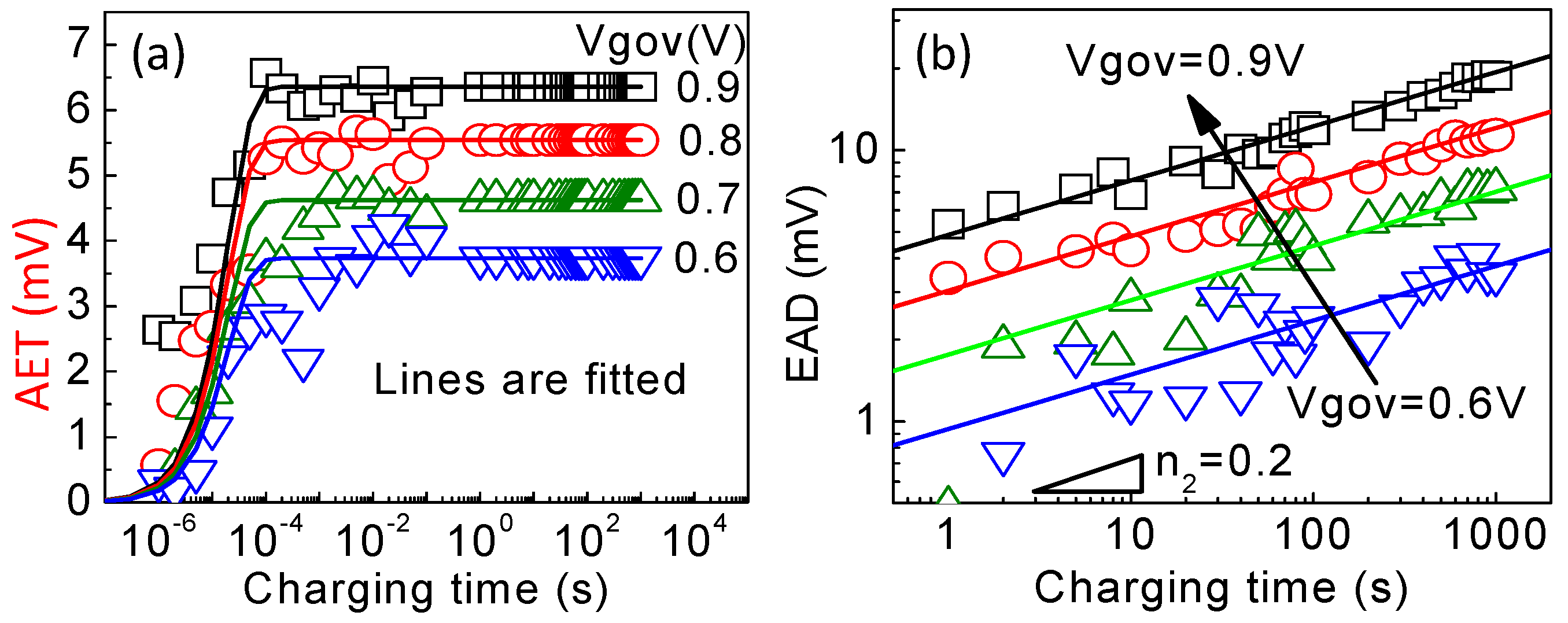 Figure 17. (a) AET kinetics under different filling Vgov; (b) EAD kinetics under different Vgov [39].
Figure 17. (a) AET kinetics under different filling Vgov; (b) EAD kinetics under different Vgov [39].
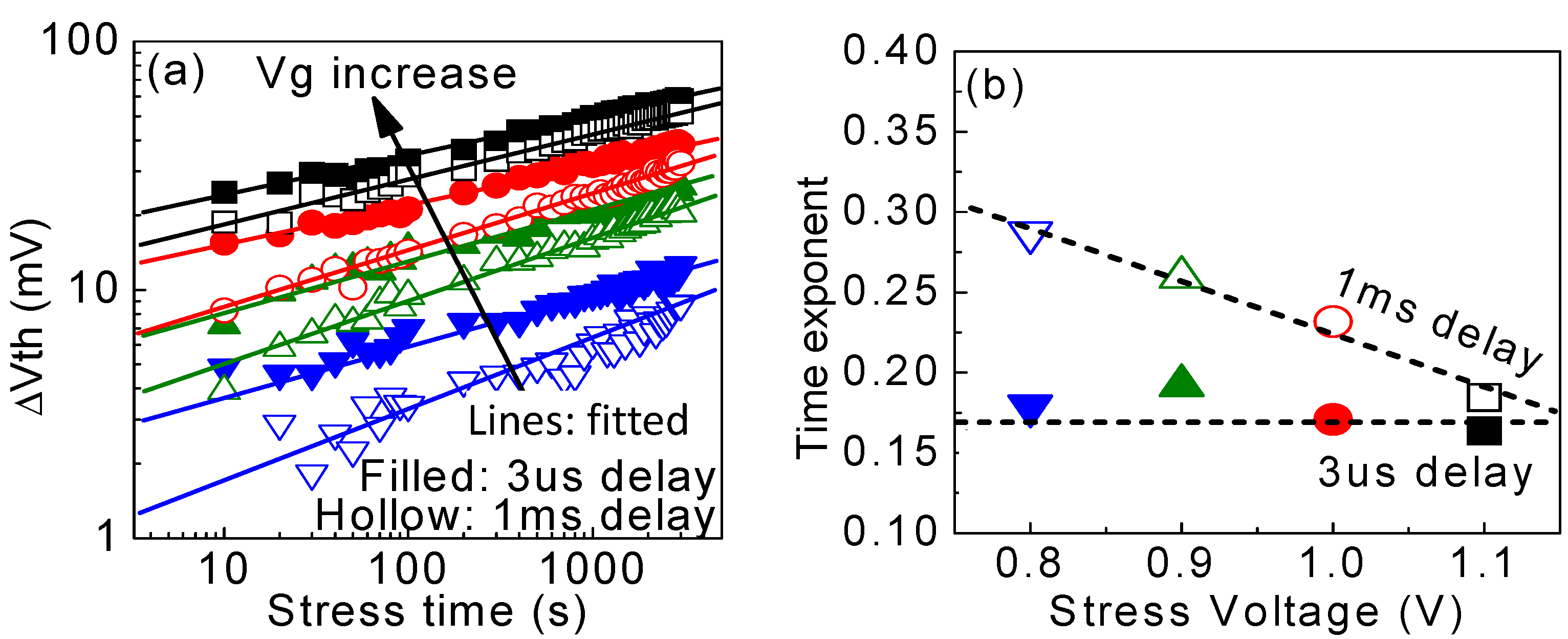 Figure 18. (a) Fitting power law with the measured total ΔVth. The lines are fitted, and the symbols are measured data. (b) The extracted power exponent depended on the delay time and stress bias [39].
Figure 18. (a) Fitting power law with the measured total ΔVth. The lines are fitted, and the symbols are measured data. (b) The extracted power exponent depended on the delay time and stress bias [39].
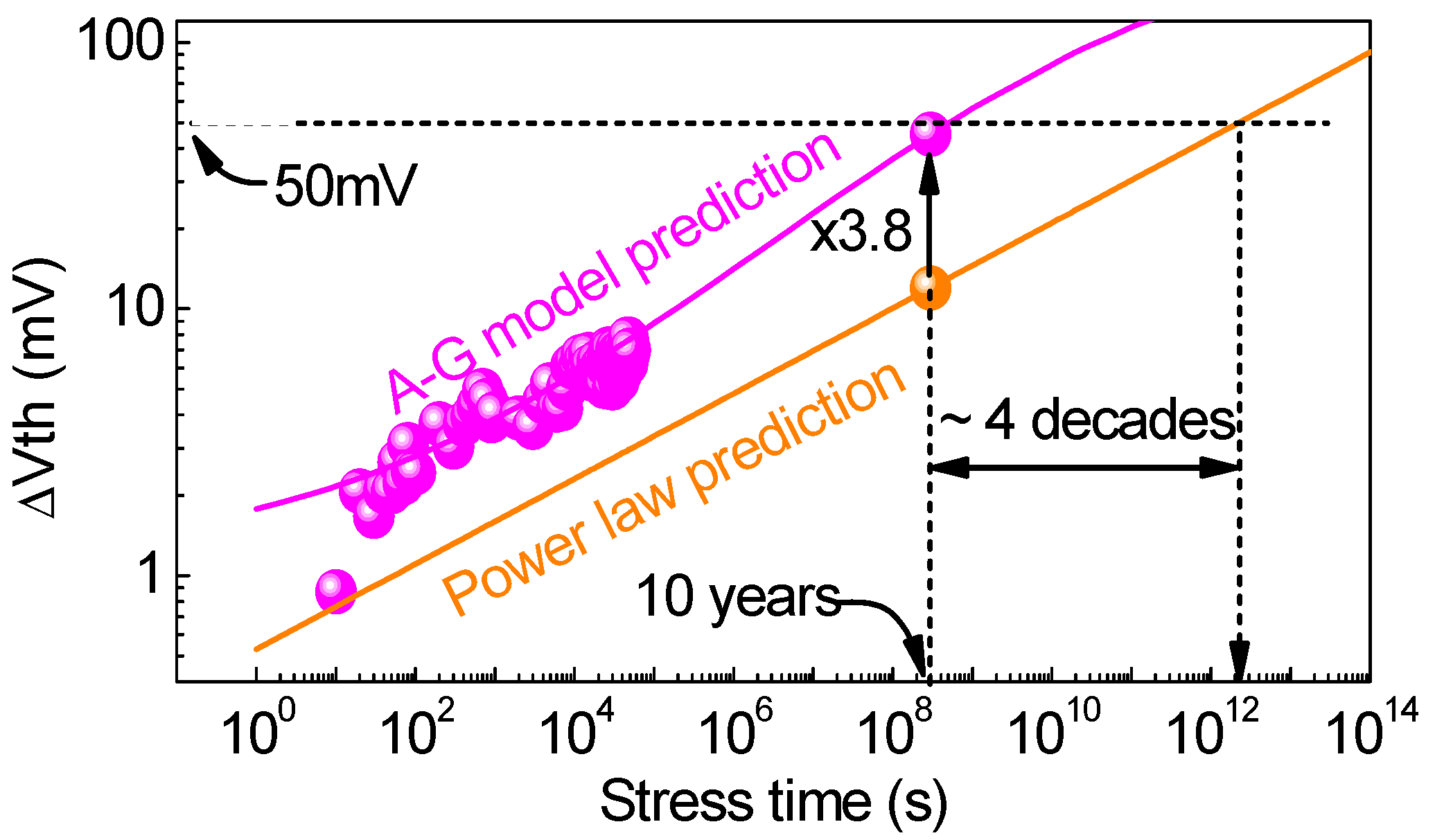 Figure 19. The AG model extracted from the accelerated PBTI tests can predict the PBTI at low biases, while the power law directly fitted with the same test data overestimates PBTI lifetime by 4 orders of magnitude [39].
Figure 19. The AG model extracted from the accelerated PBTI tests can predict the PBTI at low biases, while the power law directly fitted with the same test data overestimates PBTI lifetime by 4 orders of magnitude [39].
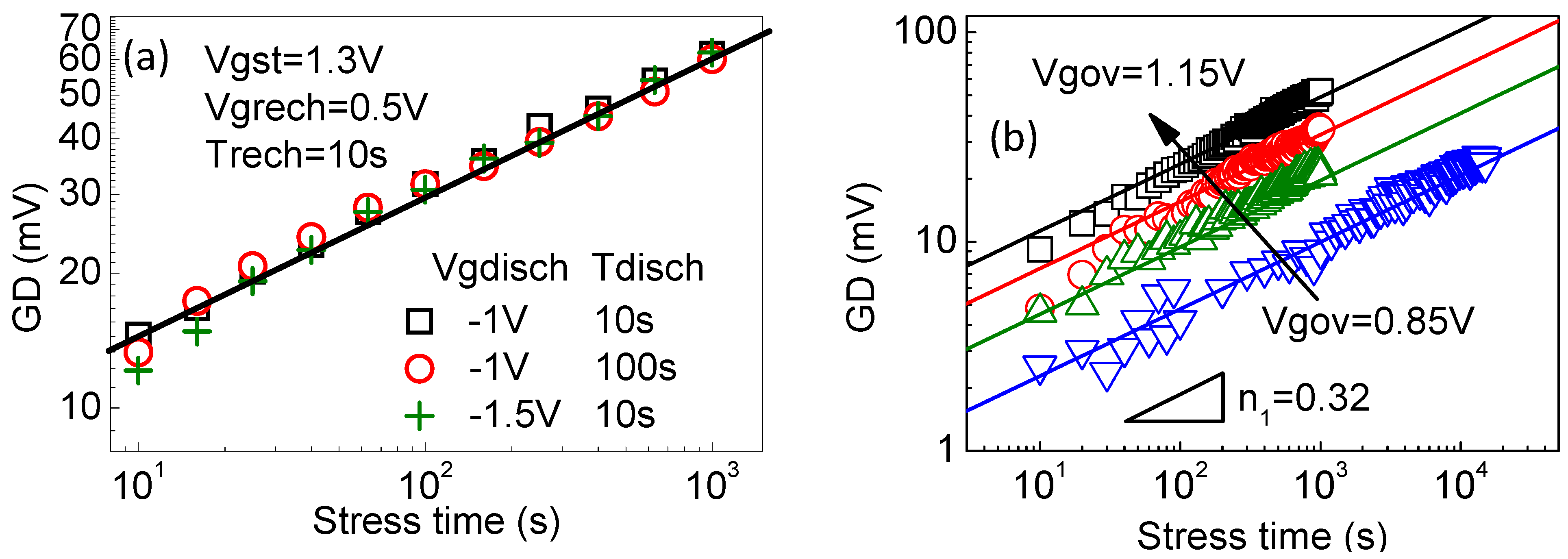 Figure 20. (a) The generated defects measured by the SDR technique were independent of the measurement conditions. (b) The GD kinetics under different stress Vgov. The power exponents were insensitive to Vgov [39].
Figure 20. (a) The generated defects measured by the SDR technique were independent of the measurement conditions. (b) The GD kinetics under different stress Vgov. The power exponents were insensitive to Vgov [39].
3. Positive Bias Temperature Instability (PBTI)
As pMOSFETs and nMOSFETs are switched on by negative and positive gate bias, respectively, NBTI mainly affects pMOSFETs, while PBTI mainly affects nMOSFETs. The relative importance of PBTI against NBTI is process dependent [23][24][25], and their impact on circuits can be added together rather than cancelling each other out. For example, Figure 5a shows that for a SRAM cell, NBTI and PBTI stresses occur in different inverters, making one inverter different from the other. Both NBTI and PBTI contribute to the reduction of the static noise margin, which is proportional to the size of butterfly eyes in Figure 5b [29]. As a result, both require modeling to optimize circuit performance.
 Figure 5. (a) When a SRAM cell holds a data bit, PBTI occurs in one of the pull-down nMOSFETs, while NBTI happens in the pull-up pMOSFET of the opposite inverters; (b) both PBTI and NBTI contribute to the reduction in the static noise margin (i.e., the size of butterfly eyes) by making the two inverters imbalance [29].
Figure 5. (a) When a SRAM cell holds a data bit, PBTI occurs in one of the pull-down nMOSFETs, while NBTI happens in the pull-up pMOSFET of the opposite inverters; (b) both PBTI and NBTI contribute to the reduction in the static noise margin (i.e., the size of butterfly eyes) by making the two inverters imbalance [29].3.1. History of PBTI
Figure 6 shows that interface states are not created for PBTI, so that PBTI only originated from negative charge formation in the gate dielectric through filling acceptor-like electron traps [40][41][42][43][44][45]. Early works showed that, if arsenium, a common dopant for Si, was left in the gate oxides, they formed electron traps [40]. Water diffused into SiO2 produces electron traps with a well-defined capture cross section of 10−17 cm2 [41]. When aluminum was used as the gate in early generation CMOS technologies, hydrogenous species also induced smaller traps with capture cross-section on the order of 10−18 cm2 [42][43][44][45].
 Figure 6. Under positive gate bias, generated defects (GDs) increased, but the negligible change in subthreshold swing (SS) indicates that interface states were not created [39].
Figure 6. Under positive gate bias, generated defects (GDs) increased, but the negligible change in subthreshold swing (SS) indicates that interface states were not created [39].When poly-si was used as the gate for the self-aligned CMOS processes, the high temperature anneal after gate implantation effectively drives these hydrogenous species out of SiO2. Figure 7 shows that there were little as-grown electron traps for poly-si gated SiO2, and electron traps must be generated by carrier tunneling through the oxide under a high oxide field [46]. When gate SiO2 is relatively thick (e.g., >5 nm), electron tunneling through gate oxide during operation is negligible, so that PBTI is insignificant. For thinner SiO2, tunneling carriers can create new electron traps. These electron traps can act as stepping-stones to form the gate-induced leakage current. They do not form stable space charges in the gate oxide and PBTI is again insignificant.
 Figure 7. There are little as-grown electron traps in the poly-Si-gated SiO2 [46].
Figure 7. There are little as-grown electron traps in the poly-Si-gated SiO2 [46].When the high-k/SiON stack is used, PBTI becomes considerable. In the early stage of high-k process development, PBTI was so severe that it limited the commercial use of the process as detailed in the next section.
3.2. PBTI as the Limiting Instability during the Early Stage of High-k Process Development
Figure 8a,b show the PBTI of a HfO2 (4 nm)/SiO2 (1 nm) stack during the development of the high-k process [24][25]. The Id-Vg recorded for the rising and falling Vg pulse edges in Figure 8a is compared in Figure 8b. The Id-Vg recorded at the falling edge was shifted in the positive direction by over half a volt from the Id-Vg of the rising edge. This was caused by electron trapping under a positive Vg during the top period of several microseconds.
 Figure 8. (a) The gate bias waveform; (b) the pulse Id-Vg recorded at the rising and falling edges of the gate bias [25].
Figure 8. (a) The gate bias waveform; (b) the pulse Id-Vg recorded at the rising and falling edges of the gate bias [25].Figure 9 shows that trapped electrons are not stable, and some of them can be lost when the falling edge time is longer than 30 μs [47]. As a result, the energy level of these electron traps is shallow and above the lower edge of silicon conduction band, Ec. These traps are as-grown and can be repeatedly charged and discharged [47].
 Figure 9. An increase in the falling edge time resulted in a lower trapping level because the trapped electrons can be detrapped before the measurement [47].
Figure 9. An increase in the falling edge time resulted in a lower trapping level because the trapped electrons can be detrapped before the measurement [47].Significant efforts have been made to overcome this huge PBTI. To find the location of these as-grown electron traps, the PBTIs of different HfO2 thicknesses were measured in Figure 10. The grey regions are the assumed trap locations. It can be seen that neither a pile-up of traps at the high-k/SiO2 interface nor a uniform distribution of traps in the high-k layer agree with the test data. Good agreement was obtained by assuming there were no traps around 1.3~1.8 nm at one or both ends of the high-k layer [47]. Figure 11 shows that PBTI reduced rapidly as the high-k layer became thinner.
 Figure 10. The location of as-grown electron traps in HfO2. Symbols represent the test data, and the lines are fitted with traps located in the grey regions [47].
Figure 10. The location of as-grown electron traps in HfO2. Symbols represent the test data, and the lines are fitted with traps located in the grey regions [47]. Figure 11. The rapid reduction of as-grown electron trapping with the downscaling of the thickness of HfO2 [47].
Figure 11. The rapid reduction of as-grown electron trapping with the downscaling of the thickness of HfO2 [47].The absence of electron trapping near the end of the high-k layer could be because electrons there can escape to the electrodes and will not form a steady space charge. It is also possible that thick high-k layer could be partially crystallized, resulting in the shallow traps. The suppression of these shallow traps by using thin high-k layers has allowed their commercial use since the advent of 45 nm CMOS technology in 2007.
3.3. PBTI of Modern High-k/SiON Stacks
Although the suppression of shallow as-grown electron traps has reduced PBTI significantly, PBTI still exists in modern commercial CMOS processes with high-k/SiON stacks [9][39][48]. One example is given in Figure 12a, which shows that PBTI is comparable with NBTI [9]. Moreover, Figure 12b shows that the recovery of PBTI is substantially less than that of NBTI. It confirms that these electron traps are energetically deeper than those responsible for the PBTI in the early stage of high-k process development as shown in Figure 8. When compared with hole traps for NBTI that pile up at the dielectric/substrate interface, the electron traps for PBTI were relatively distant from the dielectric/Si interface [47][49], which also contribute to the relative stability of PBTI.
 Figure 12. A comparison of PBTI with NBTI during stress (a) and recovery (b). (a) Shows that the PBTI was similar to NBTI during stress for this CMOS process but more stable during recovery [9].
Figure 12. A comparison of PBTI with NBTI during stress (a) and recovery (b). (a) Shows that the PBTI was similar to NBTI during stress for this CMOS process but more stable during recovery [9].To characterize the electron traps responsible for PBTI, their energy profile was probed. After charging them, as shown in Figure 13a, they were gradually lifted above the Si Ec to allow them to discharge as shown in Figure 13b [48]. The discharging at different energy levels resulted in the energy profiles in Figure 13c. These electron traps were below Si Ec under flat band conditions and peaked around 1.4 eV below the conduction band edge of HfO2.
 Figure 13. Probing the energy distribution profile of electron traps: (a) the electron traps below Si Ec were first charged; (b) applying a positive Vg will lift some charged traps above Ec for discharging, i.e., the striped region; (c) the extracted energy profile of electron traps by progressively increasing Vg for discharging [48].
Figure 13. Probing the energy distribution profile of electron traps: (a) the electron traps below Si Ec were first charged; (b) applying a positive Vg will lift some charged traps above Ec for discharging, i.e., the striped region; (c) the extracted energy profile of electron traps by progressively increasing Vg for discharging [48].3.4. As-Grown Defects for PBTI
The experience of modeling NBTI shows the importance of separating as-grown defects from the generated ones. The question is whether the electron traps observed in Figure 13 are as-grown or generated. To answer it, researchers charged and then discharged these electron traps by alternating gate bias polarity in the stage 1 of the test in Figure 14a [48]. It can be seen that the charging–discharging was recyclable, indicating that they were as-grown. To further support this, the device was heavily stressed in the stage 2. In the following stage 3, the same gate bias polarity alternation as that in the stage 1 was reapplied. Figure 14b shows that the charging–discharging of electron traps before and after the heavy PBTI stress agrees well, so that they were not affected by the stress, i.e., they are as-grown. After the heavy stress, there are electron traps that cannot be neutralized under Vg = −1.8 V at the end of stage 2. These anti-neutralization electron traps (ANET) did not exist before the heavy stress in the stage 1; thus, they were generated.
 Figure 14. (a) Test sequence for confirming the presence of as-grown defects and the generated Anti-neutralization electron traps (ANETs) by PBTI; (b) a comparison of the as-grown defects pre- and post-heavy PBTI stress [48].
Figure 14. (a) Test sequence for confirming the presence of as-grown defects and the generated Anti-neutralization electron traps (ANETs) by PBTI; (b) a comparison of the as-grown defects pre- and post-heavy PBTI stress [48].Like NBTI, the as-grown defects for PBTI can be divided into as-grown electron traps (AETs) and energy alternating defects (EADs). The energy levels of the AETs did not change with charging–discharging, while the energy levels of the EADs were lowered following charging as shown in Figure 15. This difference allows for their separation as shown in Figure 15 [39].
 Figure 15. (a) Tests for separating as-grown electron traps (AETs) from the as-grown energy-alternating defects (EADs) [39]. (b) When an AET is below Ef, it is charged. (c) The energy levels of the AETs did not change after charging. It was discharged when above the same Ef for its charging. (d) When an EAD is below Ef, it is charged. After charging, the energy level of the EAD is lowered, so that it will not be discharged under the same Ef for its charging in (e).
Figure 15. (a) Tests for separating as-grown electron traps (AETs) from the as-grown energy-alternating defects (EADs) [39]. (b) When an AET is below Ef, it is charged. (c) The energy levels of the AETs did not change after charging. It was discharged when above the same Ef for its charging. (d) When an EAD is below Ef, it is charged. After charging, the energy level of the EAD is lowered, so that it will not be discharged under the same Ef for its charging in (e).On filling kinetics, an AET can be filled rapidly, and it saturates with time. On the other hand, filling an EAD follows a power law. The saturation level of AET is determined from the measurement in Figure 15a. This saturation level is then subtracted to obtain the EAD after the AET saturation as shown by the green triangles in Figure 16. These EAD data were fitted with a power law. To obtain the AET before its saturation, the EAD power law was extrapolated to short time as shown by the green, dashed line. An AET over a short time was evaluated by subtracting the extrapolated EAD as shown by the circles in Figure 16.
 Figure 16. Extracting the kinetics of an EAD and an AET from the measured total ΔVth [39].
Figure 16. Extracting the kinetics of an EAD and an AET from the measured total ΔVth [39].The separated AET and EAD at different Vgov are given in Figure 17a,b, respectively. The power exponent of the EAD was insensitive to Vgov, and the AET followed the same kinetics after normalizing against their saturation level.
 Figure 17. (a) AET kinetics under different filling Vgov; (b) EAD kinetics under different Vgov [39].
Figure 17. (a) AET kinetics under different filling Vgov; (b) EAD kinetics under different Vgov [39].3.5. As-Grown-Generation (AG) Model of PBTI
The measured ΔVth during typical PBTI tests consists of both as-grown and generated defects. Although they could fit the power law well in Figure 18a, the extracted power exponent in Figure 18b depended on the measured delay [39]. For a delay of 1 ms, typically used in early works, the power exponent also changes with stress bias. When the extracted power law was used to predict PBTI at lower bias, Figure 19 shows that there were large discrepancies. As a result, the measured ΔVth must not be used to extract the power law directly, and it is essential to separate it into as-grown and generated defects.
 Figure 18. (a) Fitting power law with the measured total ΔVth. The lines are fitted, and the symbols are measured data. (b) The extracted power exponent depended on the delay time and stress bias [39].
Figure 18. (a) Fitting power law with the measured total ΔVth. The lines are fitted, and the symbols are measured data. (b) The extracted power exponent depended on the delay time and stress bias [39]. Figure 19. The AG model extracted from the accelerated PBTI tests can predict the PBTI at low biases, while the power law directly fitted with the same test data overestimates PBTI lifetime by 4 orders of magnitude [39].
Figure 19. The AG model extracted from the accelerated PBTI tests can predict the PBTI at low biases, while the power law directly fitted with the same test data overestimates PBTI lifetime by 4 orders of magnitude [39].After removing the contribution of as-grown defects, Figure 20a shows that the power exponent extracted from the generated defects measured by the SDR technique became independent of the measurement conditions. Moreover, Figure 20b shows that the power exponent was insensitive to the stress bias.
 Figure 20. (a) The generated defects measured by the SDR technique were independent of the measurement conditions. (b) The GD kinetics under different stress Vgov. The power exponents were insensitive to Vgov [39].
Figure 20. (a) The generated defects measured by the SDR technique were independent of the measurement conditions. (b) The GD kinetics under different stress Vgov. The power exponents were insensitive to Vgov [39].By combining the modeling of as-grown defects with that of generated defects, the as-grown-generation model in Table 1 can also be applied to PBTI [39]. Figure 19 shows that the AG model can be used to predict the PBTI at low bias.
Table 1. The formula of the as-grown-generation (AG) model for BTI.
| Defects | Formula |
|---|---|
| Saturation level of AHT/AET | ATsat=p1⋅exp(p2⋅Vgov) |
| Filling AHT/AET | AT=ATsat⋅[1−exp(−tchτ)γ] |
| EAD | EAD=g2⋅Vm2gov⋅tn2 |
| GD | GD=g1⋅Vm1gov⋅tn1 |
References
- Deal, B.E.; Sklar, M.; Grove, A.S.; Snow, E.H. Characteristics of the Surface-State Charge (Qss) of Thermally Oxidized Silicon. J. Electrochem. Soc. 1967, 114, 114–266.
- Jepson, K.O.; Svensson, C.M. Negative bias stress of MOS devices at high electric fields and degradation of MNOS devices. J. Appl. Phys. 1977, 48, 2004–2014.
- Blat, C.E.; Nicollian, E.H.; Poindexter, E.H. Mechanism of negative-bias-temperature instability. J. Appl. Phys. 1991, 69, 1712–1720.
- Ogawa, S.; Shimaya, M.; Shiono, N. Interface-trap generation at ultrathin SiO2 (4–6 nm)-Si interfaces during negative-bias temperature aging. J. Appl. Phys. 1995, 77, 1137–1148.
- Black, J.R. Electromigration Failure Modes in Aluminum Metallization for Semiconductor Devices. Proc. IEEE 1969, 57, 1587–1594.
- Chen, F.; McLaughlin, P.; Gambino, J.; Wu, E.; Demarest, J.; Meatyard, D.; Shinosky, M. The Effect of Metal Area and Line Spacing on TDDB Characteristics of 45nm Low-k SiCOH Dielectrics. In Proceedings of the 2007 IEEE International Reliability Physics Symposium Proceedings, Phoenix, AZ, USA, 15–19 April 2007; pp. 382–389.
- Nauta, P.K.; Hillen, M.W. Investigation of mobile ions in MOS structures using the TSIC method. J. Appl. Phys. 1978, 49, 2862–2865.
- Hu, C.; Tam, S.C.; Hsu, F.-C.; Ko, P.-K.; Chan, T.-Y.; Terrill, K.W. Hot-Electron-Induced MOSFET Degradation—Model, Monitor, and Improvement. IEEE J. Solid-State Circuits 1985, 20, 295–305.
- Duan, M.; Zhang, J.F.; Manut, A.; Ji, Z.; Zhang, W.; Asenov, A.; Gerrer, L.; Reid, D.; Razaidi, H.; Vigar, D.; et al. Hot carrier aging and its variation under use-bias: Kinetics, prediction, impact on Vdd and SRAM. In Proceedings of the IEEE International Electron Devices Meeting (IEDM), Washington, DC, USA, 7–9 December 2015; pp. 547–550.
- Degraeve, R.; Ogier, J.L.; Bellens, R.; Roussel, P.J.; Groeseneken, G.; Maes, H.E. A New Model for the Field Dependence of Intrinsic and Extrinsic Time-Dependent Dielectric Breakdown. IEEE Trans. Electron Devices 1998, 45, 472–481.
- Kirton, M.J.; Uren, M.J. Noise in solid-state microstructures: A new perspective on individual defects, interface states and low-frequency (1/ƒ) noise. Adv. Phys. 1989, 38, 367–468.
- Mehedi, M.; Tok, K.H.; Zhang, J.F.; Ji, Z.; Ye, Z.; Zhang, W.; Marsland, J.S. An assessment of the statistical distribution of Random Telegraph Noise Time Constants. IEEE Access 2020, 8, 1496–1499.
- Mehedi, M.; Tok, K.H.; Ye, Z.; Zhang, J.F.; Ji, Z.; Zhang, W.; Marsland, J.S. On the Accuracy in Modeling the Statistical Distribution of Random Telegraph Noise Amplitude. IEEE Access 2021, 9, 43551–43561.
- Tan, S.S.; Chen, T.P.; Ang, C.H.; Chan, L. Mechanism of nitrogen-enhanced negative bias temperature instability in pMOSFET. Microelectron. Reliab. 2005, 45, 19–30.
- Kaczer, B.; Grasser, T.; Roussel, P.J.; Franco, J.; Degraeve, R.; Ragnarsson, L.-A.; Simoen, E.; Groeseneken, G.; Reisinger, H. Origin of NBTI variability in deeply scaled pFETs. In Proceedings of the 2010 IEEE International Reliability Physics Symposium, Anaheim, CA, USA, 2–6 May 2010; pp. 26–32.
- Grasser, T. Stochastic charge trapping in oxides: From random telegraph noise to bias temperature instabilities. Microelectron. Rel. 2012, 52, 39–70.
- Zhang, J.F.; Ji, Z.; Zhang, W. As-grown-generation (AG) model of NBTI: A shift from fitting test data to prediction. Microelectron. Rel. 2018, 80, 109–123.
- Waldhoer, D.; Schleich, C.; Michl, J.; Stampfer, B.; Tselios, K.; Ioannidis, E.G.; Enichlmair, H.; Waltl, M.; Grasser, T. Toward Automated Defect Extraction From Bias Temperature Instability Measurements. IEEE Trans. Electron Devices 2021, 68, 4057–4063.
- Zhang, J.; Wang, Z.; Wang, R.; Sun, Z.; Huang, R. Body Bias Dependence of Bias Temperature Instability(BTI) in Bulk FinFET Technology. Energy Environ. Mater. 2021, 1–4.
- Lee, J. Physics-informed machine learning model for bias temperature instability. AIP Adv. 2021, 11, 025111.
- Kishida, R.; Suda, I.; Kobayashi, K. Bias Temperature Instability Depending on Body Bias through Buried Oxide (BOX) Layer in a 65 nm Fully-Depleted Silicon-On-Insulator Process. In Proceedings of the 2021 IEEE International Reliability Physics Symposium (IRPS), Monterey, CA, USA, 21–25 March 2021.
- Bhootda, N.; Yadav, A.; Neema, V.; Shah, A.P.; Vishvakarma, S.K. Series diode-connected current mirror based linear andsensitive negative bias temperature instability monitoringcircuit. Int. J. Numer. Model. 2022, 35, e2953.
- Hicks, J.; Bergstrom, D.; Hattendorf, M.; Jopling, J.; Maiz, J.; Pae, S.; Prasad, C.; Wiedemer, J. 45 nm Transistor Reliability. Intel Technol. J. 2008, 12, 131–144.
- Zhao, C.Z.; Zahid, M.B.; Zhang, J.F.; Groeseneken, G.; Degraeve, R.; De Gendt, S. Properties and dynamic behavior of electron traps in HfO2/SiO2 stacks. Microelectron. Eng. 2005, 80, 366–369.
- Zhao, C.Z.; Zhang, J.F.; Zahid, M.B.; Govoreanu, B.; Groeseneken, G.; De Gendt, S. Determination of capture cross sections for as-grown electron traps in HfO2/HfSiO stacks. J. Appl. Phys. 2006, 100, 093716.
- Asenov, A.; Cheng, B.; Dideban, D.; Kovac, U.; Moezi, N.; Millar, C.; Roy, G.; Brown, A.R.; Roy, S. Modeling and simulation of transistor and circuit variability and reliability. In Proceedings of the IEEE Custom Integrated Circuits Conference 2010, San Jose, CA, USA, 19–22 September 2010; pp. 1–8.
- Duan, M.; Zhang, J.F.; Ji, Z.; Zhang, W.; Kaczer, B.; Schram, T.; Ritzenthaler, R.; Groeseneken, G.; Asenov, A. New analysis method for time-dependent device-to-device variation accounting for within-device fluctuation. IEEE Trans. Electron Devices 2013, 60, 2505–2511.
- Duan, M.; Zhang, J.F.; Ji, Z.; Ma, J.G.; Zhang, W.; Kaczer, B.; Schram, T.; Ritzenthaler, R.; Groeseneken, G.; Asenov, A. Key issues and Techniques for Characterizing Time-Dependent Device-to-Device Variation of SRAM. In Proceedings of the 2013 IEEE International Electron Devices Meeting, Washington, DC, USA, 9–11 December 2013; pp. 774–777.
- Duan, M.; Zhang, J.F.; Ji, Z.; Zhang, W.; Kaczer, B.; Schram, T.; Ritzenthaler, R.; Groeseneken, G.; Asenov, A. Development of a Technique for Characterizing Bias Temperature Instability-Induced Device-to-Device Variation at SRAM-Relevant Conditions. IEEE Trans. Electron Devices 2014, 61, 3081–3089.
- Duan, M.; Zhang, J.F.; Ji, Z.; Zhang, W.; Kaczer, B.; Schram, T.; Ritzenthaler, R.; Thean, A.; Groeseneken, G.; Asenov, A. Time-dependent variation: A new defect-based prediction methodology. In Proceedings of the 014 Symposium on VLSI Technology (VLSI-Technology): Digest of Technical Papers, Honolulu, HI, USA, 9–12 June 2014; pp. 74–75.
- Gao, R.; Ji, Z.; Manut, A.B.; Zhang, J.F.; Franco, J.; Hatta, S.W.M.; Zhang, W.; Kaczer, B.; Linten, D.; Groeseneken, G. NBTI-Generated Defects in Nanoscaled Devices: Fast Characterization Methodology and Modeling. IEEE Trans. Electron Devices 2017, 64, 4011–4017.
- Mahapatra, S.; Goel, N.; Desai, S.; Gupta, S.; Jose, B.; Mukhopadhyay, S.; Joshi, K.; Jain, A.; Islam, A.E.; Alam, M.A. A Comparative Study of Different Physics-Based NBTI Models. IEEE Trans. Electron Devices 2013, 60, 901–916.
- Huard, V. Two independent components modeling for Negative Bias Temperature Instability. In Proceedings of the 2010 IEEE International Reliability Physics Symposium, Anaheim, CA, USA, 2–6 May 2010; pp. 33–42.
- Huard, V.; Parthasarathy, C.R.; Bravaix, A.; Hugel, T.; Guerin, C.; Vincent, E. Design-in-Reliability Approach for NBTI and Hot-Carrier Degradations in Advanced Nodes. IEEE Trans. Device Mater. Reliab. 2007, 7, 558–570.
- Ji, Z.; Hatta, S.F.W.M.; Zhang, J.F.; Ma, J.G.; Zhang, W.; Soin, N.; Kaczer, B.; De Gendt, S.; Groeseneken, G. Negative Bias Temperature Instability Lifetime Prediction: Problems and Solutions. In Proceedings of the 2013 IEEE International Electron Devices Meeting, Washington, DC, USA, 9–11 December 2013; pp. 413–416.
- Ji, Z.; Zhang, J.F.; Lin, L.; Duan, M.; Zhang, W.; Zhang, X.; Gao, R.; Kaczer, B.; Franco, J.; Schram, T.; et al. A test-proven As-grown-Generation (A-G) model for predicting NBTI under use-bias. In Proceedings of the 2015 Symposium on VLSI Technology (VLSI Technology), Kyoto, Japan, 16–18 June 2015; pp. 36–37.
- Gao, R.; Ji, Z.; Hatta, S.M.; Zhang, J.F.; Franco, J.; Kaczer, B.; Zhang, W.; Duan, M.; De Gendt, S.; Linten, D.; et al. Predictive As-grown-Generation (A-G) model for BTI-induced device/circuit level variations in nanoscale technology nodes. In Proceedings of the 2016 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 3–7 December 2016; pp. 778–781.
- Gao, R.; Manut, A.B.; Ji, Z.; Ma, J.; Duan, M.; Zhang, J.F.; Franco, J.; Hatta, S.W.M.; Zhang, W.; Kaczer, B.; et al. Reliable time exponents for long term prediction of negative bias temperature instability by extrapolation. IEEE Trans. Electron Devices 2017, 64, 1467–1473.
- Gao, R.; Ji, Z.; Zhang, J.F.; Marsland, J.; Zhang, W.D. As-grown-Generation Model for Positive Bias Temperature Instability. IEEE Trans. Electron Devices 2018, 65, 3662–3668.
- DeKeersmaecker, R.F.; DiMaria, D.J. Electron trapping and detrapping characteristics of arsenic-implanted SiO2 layers. J. Appl. Phys. 1980, 51, 1085–1101.
- Nicollian, E.H.; Berglund, C.N.; Schmidt, P.F.; Andrews, J.M. Electrochemical Charging of Thermal SiO2 Films by Injected Electron Currents. J. Appl. Phys. 1971, 42, 5654–5664.
- Zhang, J.F. Oxide defects. In Bias Temperature Instabilities for Devices and Circuits; Springer: Berlin/Heidelberg, Germany, 2014; pp. 253–285.
- Zhang, J.F.; Taylor, S.; Eccleston, W. Electron Trap Generation in Thermally Grown Silicon Dioxide Under Fowler-Nordheim Stress. J. Appl. Phys. 1992, 71, 725–734.
- Zhang, J.F.; Taylor, S.; Eccleston, W. A Quantitative Investigation of Electron Detrapping in SiO2 Under Fowler-Nordheim Stress. J. Appl. Phys. 1992, 71, 5989–5996.
- Zhang, J.F.; Taylor, S.; Eccleston, W. A Comparative Study of The Electron Trapping and Thermal Detrapping in SiO2 Prepared by Plasma and Thermal Oxidation. J. Appl. Phys. 1992, 72, 1429–1435.
- Zhang, W.D.; Zhang, J.F.; Lalor, M.; Burton, D.; Groeseneken, G.; Degraeve, R. Two types of neutral electron traps generated in the gate silicon dioxide. IEEE Trans. Electron Devices 2002, 49, 1868–1875.
- Zhang, J.F.; Zhao, C.Z.; Zahid, M.B.; Groeseneken, G.; Degraeve, R.; De Gendt, S. An assessment of the location of as-grown electron traps in HfO2/HiSiO stacks. IEEE Electron Device Lett. 2006, 27, 817–820.
- Duan, M.; Zhang, J.F.; Ji, Z.; Zhang, W.; Vigar, D.; Asenov, A.; Gerrer, L.; Chandra, V.; Aitken, R.; Kaczer, B. Insight into Electron Traps and Their Energy Distribution under Positive Bias Temperature Stress and Hot Carrier Aging. IEEE Trans. Electron Devices 2016, 63, 3642–3648.
- Zhang, J.F.; Chang, M.H.; Ji, Z.; Lin, L.; Ferain, I.; Groeseneken, G.; Pantisano, L.; De Gendt, S.; Heyns, M.M. Dominant layer for stress-induced positive charges in Hf-based gate stacks. IEEE Electron Device Lett. 2008, 29, 360–1363.
More
Information
Subjects:
Engineering, Electrical & Electronic
Contributors
MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register
:
View Times:
10.1K
Revisions:
2 times
(View History)
Update Date:
13 May 2022
Notice
You are not a member of the advisory board for this topic. If you want to update advisory board member profile, please contact office@encyclopedia.pub.
OK
Confirm
Only members of the Encyclopedia advisory board for this topic are allowed to note entries. Would you like to become an advisory board member of the Encyclopedia?
Yes
No
${ textCharacter }/${ maxCharacter }
Submit
Cancel
Back
Comments
${ item }
|
More
No more~
There is no comment~
${ textCharacter }/${ maxCharacter }
Submit
Cancel
${ selectedItem.replyTextCharacter }/${ selectedItem.replyMaxCharacter }
Submit
Cancel
Confirm
Are you sure to Delete?
Yes
No


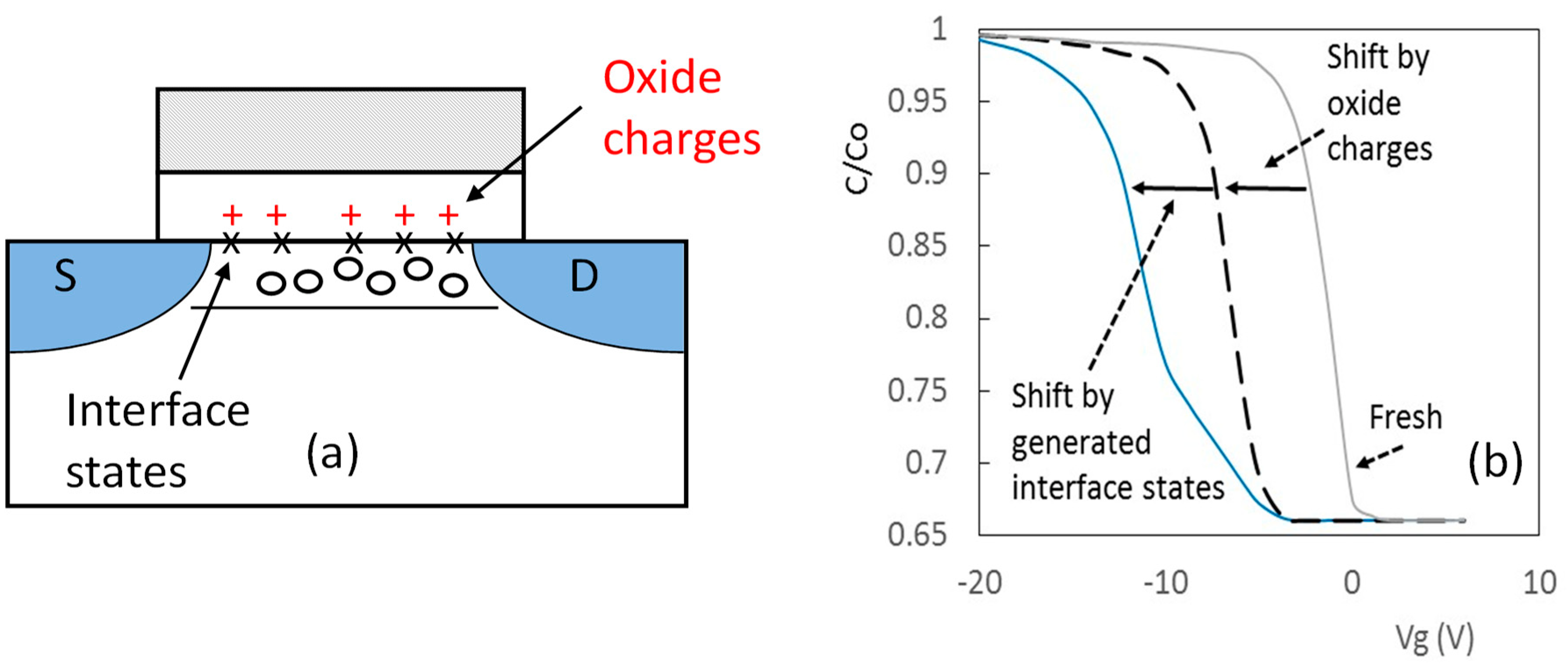 Figure 3. (a) A schematic illustration of oxide charges and the generated interface states; (b) the effect of NBTI on capacitance versus gate voltage characteristics: positive charges in gate oxide lead to a parallel shift and the generated interface states result in a nonparallel shift [
Figure 3. (a) A schematic illustration of oxide charges and the generated interface states; (b) the effect of NBTI on capacitance versus gate voltage characteristics: positive charges in gate oxide lead to a parallel shift and the generated interface states result in a nonparallel shift [

