
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Jehad Alzabut | -- | 640 | 2022-04-27 11:15:35 | | | |
| 2 | Lindsay Dong | + 342 word(s) | 982 | 2022-04-28 11:22:27 | | | | |
| 3 | Lindsay Dong | + 188 word(s) | 1170 | 2022-04-29 08:26:45 | | | | |
| 4 | Lindsay Dong | + 313 word(s) | 1483 | 2022-04-29 08:45:32 | | | | |
| 5 | Lindsay Dong | + 730 word(s) | 2213 | 2022-04-29 09:28:14 | | |
Video Upload Options
Oscillation is one of the important branches in applied mathematics and can be induced or destroyed by the introduction of nonlinearity, delay, or a stochastic term. The oscillation of differential and difference equations contributes to many realistic applications, such as torsional oscillations, the oscillation of heart beats, sinusoidal oscillation, voltage-controlled neuron models, and harmonic oscillation with damping.
1. Introduction
2. Preliminaries
The empty sums and products were taken to be zero and one, respectively. Denote by he set of all natural numbers, the set of all real numbers, and the set of all positive real numbers. Define by and for any a, such that .
Definition 1 ([12][13]). The Euler gamma function is defined by:
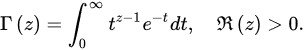
Using its reduction formula, the Euler gamma function can also be extended to the half-plane except for
Definition 2 ([14]). The generalized falling function is defined by:
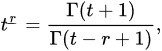
for those values of t and r such that the right-hand side of this equation makes sense. If is a nonpositive integer and is not a nonpositive integer, then we use the convention that . The generalized rising function is defined by:
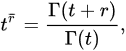
for those values of t and r so that the right-hand side of this equation is sensible. If t is a nonpositive integer, but is not a nonpositive integer, then we use the convention that
Definition 3 ([15]). Let and . The first-order forward (delta) and backward (nabla) differences of u are defined by:
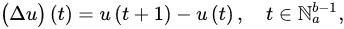
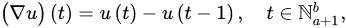
respectively. The -order delta and nabla differences of u are defined recursively by
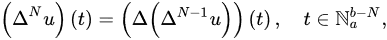
and:
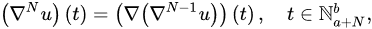
respectively.
Definition 4 ([14]). Let and . Then, the -order delta fractional sum of u based at a is defined by:
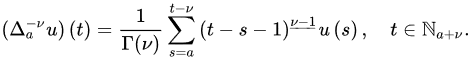
Definition 5 ([14]). Let and . Then, the -order nabla fractional sum of u based at a is defined by:

Definition 6 ([14]). Let , and choose such that . The -order Riemann–Liouville delta fractional difference of u is defined by:
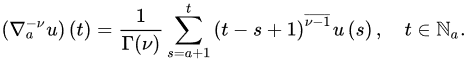
Definition 7 ([14]). Let , and choose such that . Then, the -order Riemann–Liouville nabla fractional difference of u is defined by:
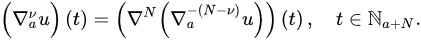
Definition 8 ([16]). Let , and . Then, the -order Caputo delta fractional difference of u is defined by:
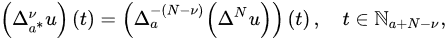
where . If , then:
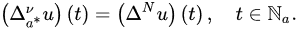
Definition 9 ([17]). Let and . Then, the -order Caputo nabla fractional difference of u is defined by:
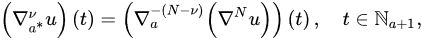
where .
3. Oscillation
3.1. Oscillatory Behavior of Delta Fractional Difference Equations
Consider the following higher-order nonlinear delta fractional difference equations involving the Riemann–Liouville and the Caputo operators of arbitrary order:
and:
Here, and choose such that ; and are continuous. A solution u of (1) (or (2)) is said to be oscillatory if for every natural number M, there exists such that ; otherwise, it is called non-oscillatory. An equation is said to be oscillatory if all of its solutions are oscillatory.
Let be continuous and , be positive real numbers. We make the following assumptions:
(A1) The functions satisfy the sign condition , , , ;
(A2) ;
(A3) .
In [18], Senem et al. established some oscillation theorems given in the sequel.
Theorem 1 ([18]). Let (A1)–(A2) be satisfied with . If:
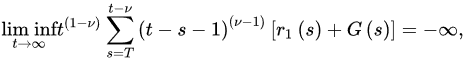
and:
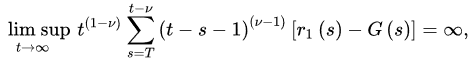
for every sufficiently large T, where:
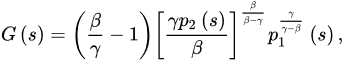
then Equation (1) is oscillatory.
Theorem 2 ([18]). Let and (A1)–(A3) be satisfied with . If
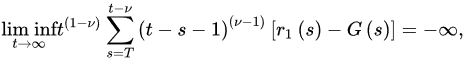
and:
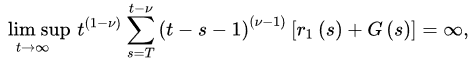
for every sufficiently large T, where G is defined as in Theorem 1, then every bounded solution of Equation (1) is oscillatory.
Theorem 3 ([18]). Let (A1) and (A2) be satisfied with . If:
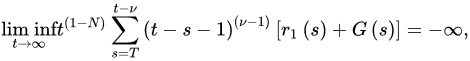
and:
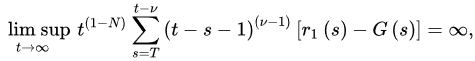
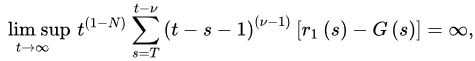
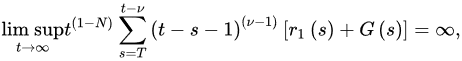
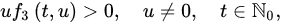
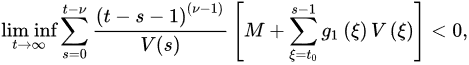
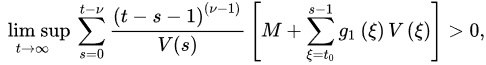
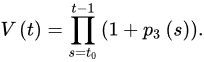
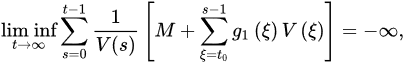
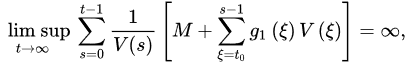

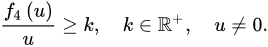
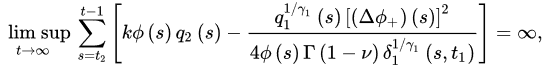
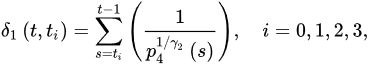
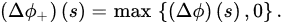


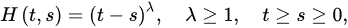
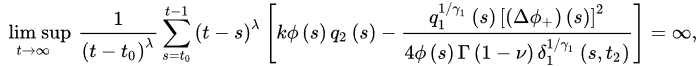
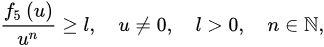
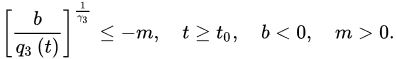
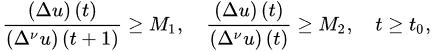
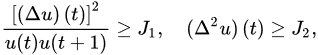
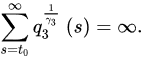

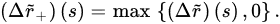
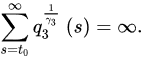
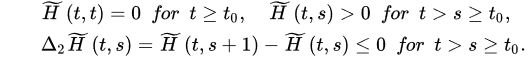
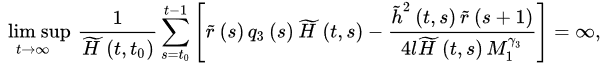
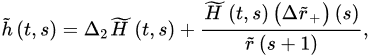
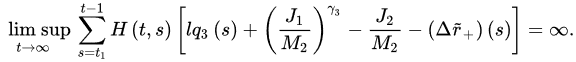
3.2. Oscillatory Behavior of Nabla Fractional Difference Equations
Let , and choose such that . Take p, , , ; , ; ; , ; w, ; q, ; x, ; ; y is a positive function defined on , , are positive real numbers; are the ratios of odd positive integers with .
We make the following assumptions:
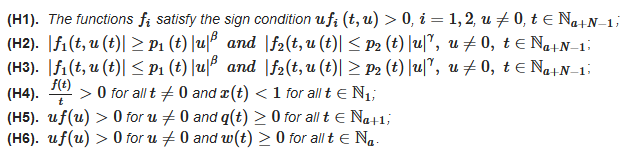
Alzabut et al. [24] initiated the study of the oscillation of solutions of nabla fractional difference equations. In [24], the authors established several oscillation criteria for the following nonlinear nabla fractional difference equations involving the Riemann–Liouville and Caputo operators of arbitrary order.
and:
A solution u of (30) (or (31)) is said to be oscillatory if for every natural number M, there exists such that ;otherwise, it is called non-oscillatory. An equation is said to be oscillatory if all of its solutions are oscillatory.
Theorem 37 ([24]). Let and Condition (H1) hold. If:
Theorem 46 ([25]).
Theorem 47 ([25]).
Theorem 48 ([25]).
for sufficiently large T, where H is defined in Theorem 45, then every bounded solution of Equation (31) is oscillatory.
In alignment with the above works, Abdalla et al. [26] investigated the oscillation of solutions for nabla fractional difference equations with mixed nonlinearities of the forms:
Theorem 49 ([26]). Let:
then Equation (32) is oscillatory.
Corollary 3 ([26]). Let in (32), then . Suppose , , .If (35) and (36) hold for some constant , then Equation (32) is oscillatory.
Corollary 4 ([26]). Let in (32), then . Suppose , , .If (35) and (36) hold for some constant , then Equation (32) is oscillatory.
Corollary 5 ([26]). Let:
Theorem 50 ([26]). Assume that Condition (34) holds. If:
Corollary 6 ([26]).
Corollary 7 ([26]).
Corollary 8 ([26]).
Following the above trend, in [27], Alzabut et al. considered the following forced and damped nabla fractional difference equation:
Motivated by the paper [24], the authors [28] investigated the oscillation of a nonlinear fractional nabla difference system of the form:
Theorem 55 ([29]). Let Condition (H6) hold. If the inequality:
References
- Diethelm, K. The Analysis of Fractional Differential Equations; Lecture Notes in Mathematics; Springer: Berlin, Germany, 2010; Volume 2004.
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; A Wiley-Interscience Publication; John Wiley & Sons, Inc.: New York, NY, USA, 1993.
- Podlubny, I. Fractional Differential Equations. In Mathematics in Science and Engineering; Academic Press, Inc.: San Diego, CA, USA, 1999; Volume 198.
- Debnath, L. Recent Applications of Fractional Calculus to Science and Engineering. Int. J. Math. Math. Sci. 2003, 2003, 753601.
- Holm, M. The Theory of Discrete Fractional Calculus, Development and Application. Ph.D. Dissertation, Nebraska University, Lincoln, NE, USA, 2011.
- Agarwal, R.P. Certain fractional q-integrals and q-derivatives. Math. Camb. Philos. Soc. 1969, 66, 365–370.
- Atici, F.M.; Eloe, P.W. A transform method in discrete fractional calculus. Int. J. Differ. Equ. 2007, 2, 165–176.
- Atici, F.M.; Eloe, P.W. Initial value problems in discrete fractional calculus. Proc. Am. Math. Soc. 2009, 137, 981–989.
- Anastassiou, G.A. Discrete fractional Calculus and Inequalities. arXiv 2009, arXiv:0911.3370.
- Atici, F.M.; Eloe, P.W. Discrete fractional calculus with the nabla operator. Electron. J. Qual. Theory Differ. Equ. 2009, 3, 1–12.
- Goodrich, C.; Peterson, A.C. Discrete Fractional Calculus; Springer International Publishing: Berlin/Heidelberg, Germany, 2018.
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; North-Holland Mathematics Studies; Elsevier Science B.V.: Amsterdam, The Netherlands, 2006.
- Podlubny, I. Fractional differential equations. An introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. In Mathematics in Science and Engineering; Academic Press, Inc.: San Diego, CA, USA, 1999.
- Goodrich, C.; Peterson, A.C. Discrete Fractional Calculus; Springer: Cham, Switzerland, 2015.
- Bohner, M.; Peterson, A. Dynamic Equations on Time Scales: An Introduction with Applications; Birkhäuser Boston, Inc.: Boston, MA, USA, 2001.
- Abdeljawad, T. On Riemann and Caputo fractional differences. Comput. Math. Appl. 2011, 62, 1602–1611.
- Anastassiou, G.A. Nabla discrete fractional calculus and nabla inequalities. Math. Comput. Model. 2010, 51, 562–571.
- Kısalar, S.; Yıldız, M.K.; Aktoprak, E. Oscillation of higher order fractional nonlinear difference equations. Int. J. Differ. Equ. 2015, 10, 201–212.
- Li, W.N. Oscillation results for certain forced fractional difference equations with damping term. Adv. Differ. Equ. 2016, 2016, 70.
- Secer, A.; Adiguzel, H. Oscillation of solutions for a class of nonlinear fractional difference equations. J. Nonlinear Sci. Appl. 2016, 9, 5862–5869.
- Chatzarakis, G.E.; Gokulraj, P.; Kalaimani, T.; Sadhasivam, V. Oscillatory solutions of nonlinear fractional difference equations. Int. Differ. Equ. 2018, 13, 19–31.
- Adiguzel, H. Oscillation theorems for nonlinear fractional difference equations. Bound. Value Probl. 2018, 2018, 178.
- Adiguzel, H. Oscillatory behavior of solutions of certain fractional difference equations. Adv. Differ. Equ. 2018, 2018, 445.
- Alzabut, J.O.; Abdeljawad, T. Sufficient conditions for the oscillation of nonlinear fractional difference equations. J. Fract. Calc. Appl. 2014, 5, 177–187.
- Abdalla, B.; Abodayeh, K.; Abdeljawad, T.; Alzabut, J. New oscillation criteria for forced nonlinear fractional difference equations. Vietnam. J. Math. 2017, 45, 609–618.
- Abdalla, B.; Alzabut, J.; Abdeljawad, T. On the oscillation of higher order fractional difference equations with mixed nonlinearities. Hacet. J. Math. Stat. 2018, 47, 207–217.
- Alzabut, J.; Abdeljawad, T.; Alrabaiah, H. Oscillation criteria for forced and damped nabla fractional difference equations. J. Comput. Anal. Appl. 2018, 24, 1387–1394.
- Li, W.N.; Sheng, W. Sufficient conditions for oscillation of a nonlinear fractional nabla difference system. Springer Plus 2016, 5, 1178.
- Li, W.; Sheng, W.; Zhang, P. Oscillatory properties of certain nonlinear fractional nabla difference equations. J. Appl. Anal. Comput. 2018, 8, 1910–1918.




