Oscillation is one of the important branches in applied mathematics and can be induced or destroyed by the introduction of nonlinearity, delay, or a stochastic term. The oscillation of differential and difference equations contributes to many realistic applications, such as torsional oscillations, the oscillation of heart beats, sinusoidal oscillation, voltage-controlled neuron models, and harmonic oscillation with damping.
- forward (delta) difference equation
- backward (nabla) difference equation
- oscillation of solutions
1. Introduction
2. Preliminaries
The empty sums and products were taken to be zero and one, respectively. Denote by he set of all natural numbers, the set of all real numbers, and the set of all positive real numbers. Define by and for any a, such that .
Definition 1 ([12][13][19,20]). The Euler gamma function is defined by:
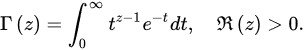
Using its reduction formula, the Euler gamma function can also be extended to the half-plane except for
Definition 2 ([14]). The generalized falling function is defined by:
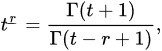
for those values of t and r such that the right-hand side of this equation makes sense. If is a nonpositive integer and is not a nonpositive integer, then we use the convention that .
Using Theits generalized rising funreduction is defined by:
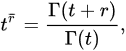
fformula, those values of t and r so that the right-hand side of this equation is sensible. If t is a nonpositive integer, but is not a nonpositive Euler gamma function can also be integer, then we use the conventionxtended to the half-plane that
Definition 3 ([15]). Lexcept for and .
Definition 2 ([21]). The first-ordgener forward (delta) and backward (nabla) differences of u are alized falling function is defined by:
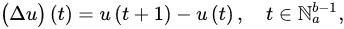
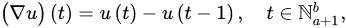
respectively. The -order delta and nabla differences of u are defined recursively by
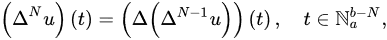
and:
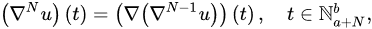
respectively.
Definition 4 ([14]). Let and . Then, the -order delta fractional sum of u based at a is defined by:
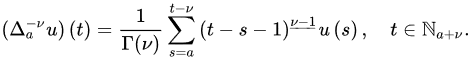
Definition 5 ([14]). Let and . Then, the -
ford thoser nabla fractional sum of u based at a is defined by:

Definition 6 ([14]). Let values of t and r such that the right-hand side of this equation makes sense. If , is a nd choosonpositive integer and isuch not a nonpositive integer, then we use the convention that . The -ord. Ther Riemann–Liouville delta fractional difference of u generalized rising function is defined by:
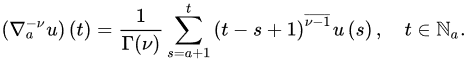
Definition 7 ([14]). Let , and choose such that . Then, the -
ford thoser Riemann–Liouville nabla fractional difference of u is defined by:
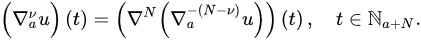
Definition 8 ([16]). Le values of t and r so that the right-hand side of this equation is sensible. If t is a nonpositive integer, but , ais nd ot .a Thennonpositive integer, the -ordn wer Caputo delta fractional difference of u is defined by:
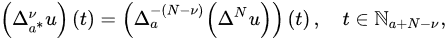
wuse the convention there at . If , then:
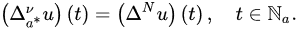
Definition 93 ([17][22]). Let and . Then, the . The first-order Caputo nabla fractionalforward (delta) and backward (nabla) differences of u isare defined by:
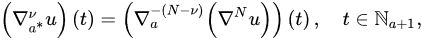
where .
3. Oscillation
3.1. Oscillatory Behavior of Delta Fractional Difference Equations
Consider the following higher-order nonlinear delta fractional difference equations involving the Riemann–Liouville and the Caputo operators of arbitrary order:
and:
Here, and choose such that ; and are continuous. A solution u of (1) (or (2)) is said to be oscillatory if for every natural number M, there exists such that ; otherwise, it is called non-oscillatory. An equation is said to be oscillatory if all of its solutions are oscillatory.
Let be continuous and , be positive real numbers. We make the following assumptions:
(A1) The functions satisfy the sign condition , , , ;
(A2) ;
(A3) .
In [18], Senem et al. established some oscillation theorems given in the sequel.
Theorem 1 ([18]). Lret (A1)–(A2) bspe satisfied with . If:
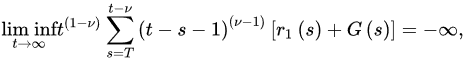
and:
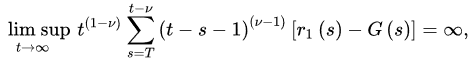
for ectivery sufficiently large T, wher. The:
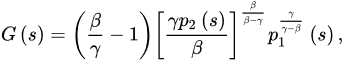
then Equation (1) is oscillatory.
Theorem 2 ([18]). Let and (A1)–(A3) be satisfied with . If
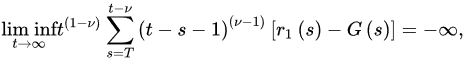
and:
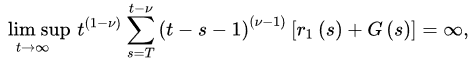
f-or devery sufficiently large T, where G is defined as in Theorem 1, then every bounded solution of Equation (1) is oscir delta and nabllatory.
Theorem 3 ([18]). Let (A1) and (A2) be satisfied with . If:
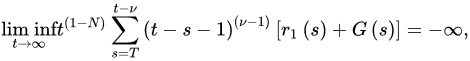
and:
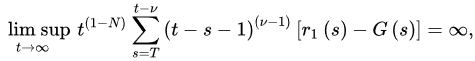
iffor every sufficiently large T, where G is defined as in Theorem 1, then Equation (2)rences of u is oscillatory.
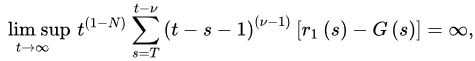
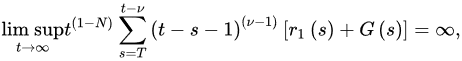
and:
respectively.
Definition 4 ([21]). Let
such that: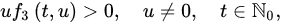
and
for .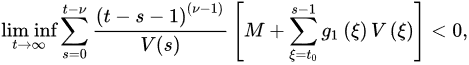
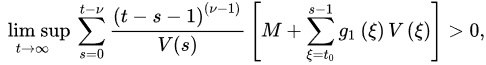
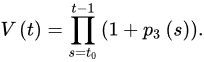
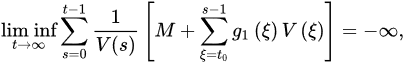
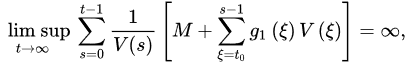
:

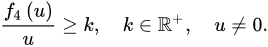
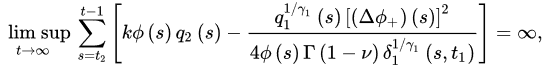
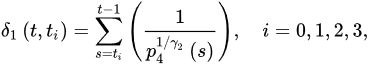
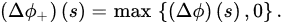
 If:
If:

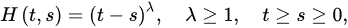 we have the following corollary.
we have the following corollary.
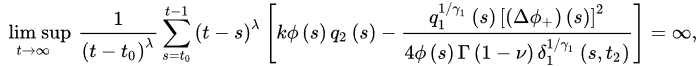
Definition 5 ([21]). Let
; is a quotient of odd positive integers; is a positive sequence, and is a continuous function such that: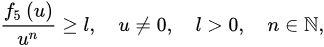
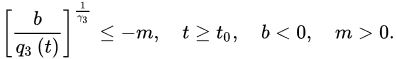 We also assume:
We also assume:
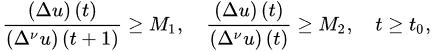 for some positive constants ,
for some positive constants ,and
and for all and. Then, the
, and: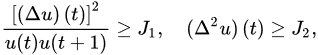 for some positive constants and .
Theorem 9 ([21]). Assume:
for some positive constants and .
Theorem 9 ([21]). Assume:
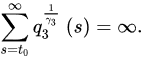 Fu-orthdermore, assume that there exists a positive sequence r˜ such r nabla fracthat:
Fu-orthdermore, assume that there exists a positive sequence r˜ such r nabla fracthat:
 where:
where:
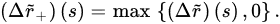
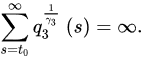
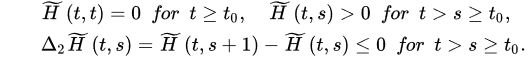
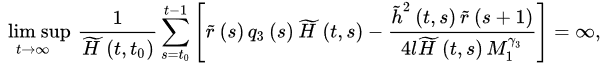
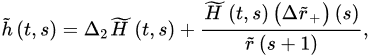
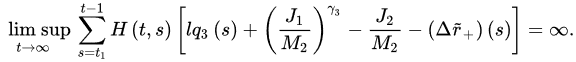
3.2. Oscillatory Behavior of Nabla Fractional Difference Equations
Let ,Definition 6 ([21]). and choose Let such that . Take p, , , ;and choose , ; ; ,such that ; w,. The ; q, ; x, ; ; -order Riemann–Liouville delta fractional difference of u is defined by is a positive function defined on:
, , are positive real numbers; are the ratios of odd positive integers with .
We make the following assumptions:
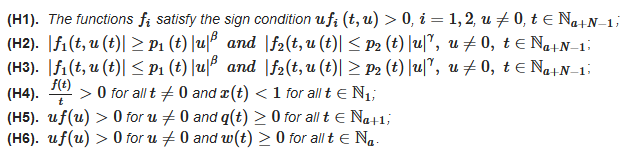
Alzabut et al. [24] initiated the study of the oscillation of solutions of nabla fractional difference equations. In [24], the authors established several oscillation criteria for the following nonlinear nabla fractional difference equations involving the Riemann–Liouville and Caputo operators of arbitrary order.
and:
A solution u of
Definition 7 (30[21]). (or (31)) is said to be oscillatory if for every natural number M, there existsLet such that ;otherwise, it is called non-oscillatory. An equation is said to be oscillatory if all of its solutions are oscillatory.
Theorem 37 ([24]). Let, and Condition (H1) chold. If:
Theorem 46 ([25]).
Theorem 47 ([25]).
Theorem 48 ([25]).
f-or sufficidently large T, where H is defined in Theorem 45, then every bounded solution of Equation (31) is oscir Riemann–Liouvillatory.
In alignment with the above works, Abdalla et al. [26] investigated the oscillation of solutions for nabla fractional difference equations with mixed nonlinearities of the forms:
Theorem 49 ([26]). Let:
then Eqof uation (32) is oscillatory.
, , .If (35) and (36) hold for some constant , then Equation (32) is oscillatory.
Corollary 4 ([26]). Let in (32), then . Suppose , , .If (35) and (36) hold for some constant , then Equation (32) is oscillatory.
Corollary 5 ([26]). Let:
Theorem 50 ([26]). Assume that Condition (34) holds. If:
Corollary 6 ([26]).
Corollary 7 ([26]).
Corollary 8 ([26]).
Following the above trend, in [27], Alzabut et al. considered the following forced and damped nabla fractional difference equation:
Motivated by the paper [24], the authors [28] investigated the oscillation of a nonlinear fractional nabla difference system of the form:
Theorem 55 ([29]). Let Condition (H6) hold. If the inequality:
