Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Furong TANG
 -- 1415 2022-04-22 03:37:10 |
2 format correct
Catherine Yang
 Meta information modification 1415 2022-04-22 04:13:10 |

Video Upload Options

We provide professional Video Production Services to translate complex research into visually appealing presentations. Would you like to try it?
No, upload directly Yes

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Tang, F.; Chao, J.; Xu, L. Developments in Algorithms for Sequence Alignment. Encyclopedia. Available online: https://encyclopedia.pub/entry/22148 (accessed on 15 November 2024).
Tang F, Chao J, Xu L. Developments in Algorithms for Sequence Alignment. Encyclopedia. Available at: https://encyclopedia.pub/entry/22148. Accessed November 15, 2024.
Tang, Furong, Jiannan Chao, Lei Xu. "Developments in Algorithms for Sequence Alignment" Encyclopedia, https://encyclopedia.pub/entry/22148 (accessed November 15, 2024).
Tang, F., Chao, J., & Xu, L. (2022, April 22). Developments in Algorithms for Sequence Alignment. In Encyclopedia. https://encyclopedia.pub/entry/22148
Tang, Furong, et al. "Developments in Algorithms for Sequence Alignment." Encyclopedia. Web. 22 April, 2022.
Developments in Algorithms for Sequence Alignment
Edit
This entry is adapted from the peer-reviewed paper 10.3390/biom12040546

Pairwise sequence alignment is the basis of multiple sequence alignment and mainly divided into local alignment and global alignment. The former is to find and align the similar local region, and the latter is end-to-end alignment. A commonly used global alignment algorithm is the Needleman–Wunsch algorithm, which has become the basic algorithm that is used in many types of multiple sequence alignment software. The algorithm usually consists of two steps: one is calculating the states of the dynamic programming matrix; and the other is tracking back from the final state to the initial state of the dynamic programming matrix to obtain the solution of alignment. Time and space complexity of pairwise sequence alignment algorithms based on dynamic programming is O(l1l2), where l1 and l2 are the lengths of the two sequences to be aligned. Such overheads are acceptable for short sequences but not for sequences with more than several thousand sites. As a space-saving strategy of the dynamic programming algorithm, the Hirschberg algorithm is able to complete alignment by the space complexity of O(l) without any sacrifice of quality.

heuristic alignment algorithms alignment scoring pairwise sequence alignment

1. Divide and Conquer

One of the heuristic methods is based on divide and conquer. In such methods, homologous segments (or seeds) are found and used as the “anchors” for the alignment. Each anchor point can divide the dynamic programming matrix into four sub-matrices located at the four corners. Backtracking always goes toward the upper left direction, and these anchors are regarded as the waypoints that the optimal path must pass; therefore, the sub-matrices located at the lower left and upper right are useless and naturally disregarded. When more anchor points distributed throughout the sequences are found, the scale of the dynamic programming matrix can be greatly reduced, thereby reducing the time and space complexity (Figure 1A).
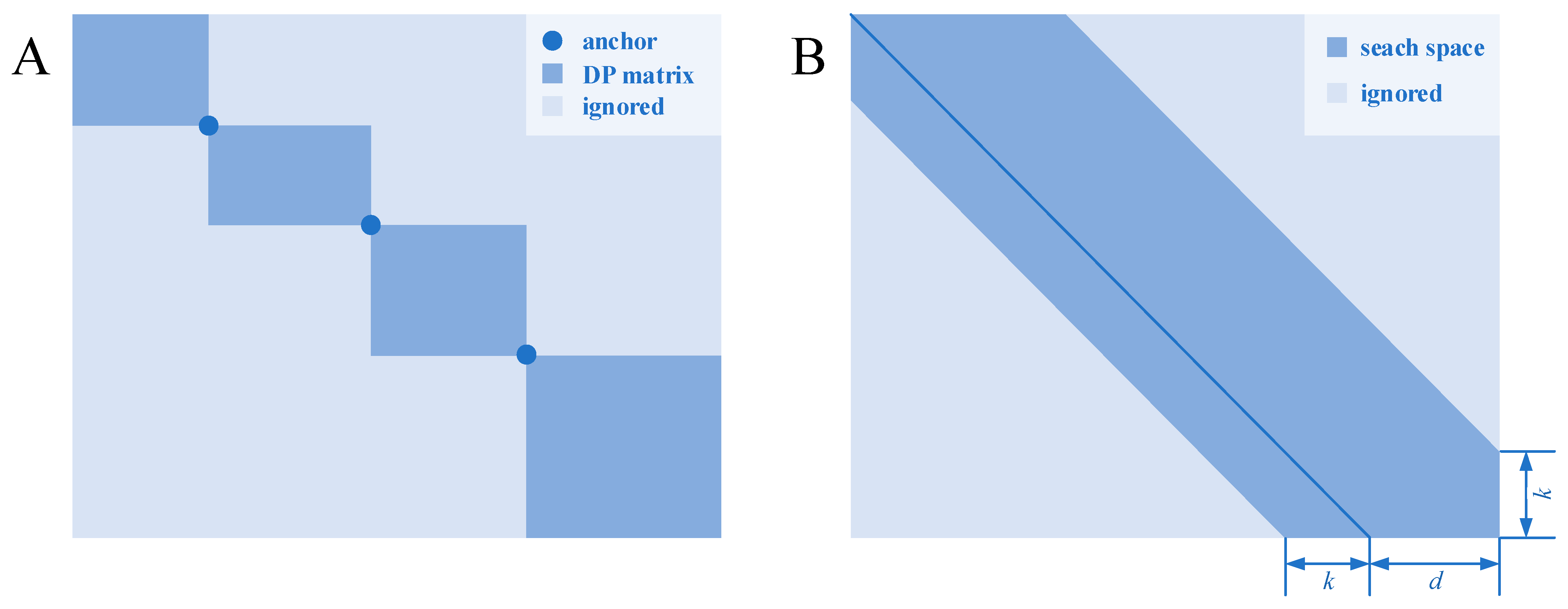
/media/item_content/202204/62620eea80414biomolecules-12-00546-g001.png
Figure 1. Two heuristic algorithms for pairwise sequence alignment. (A) A dynamic programming matrix, which is separated by several anchors, which is certain to be in the optimal path. (B) A shape-based bounded dynamic programming matrix in which the light blue block is calculation-free because these states are thought to be less likely to be in the optimal path.
Many alignment algorithms are designed to find such seeds to accelerate alignment. FASTA [1][2] and BLAST [3] are two of the classic ones. They both search for common substrings in a way similar to the Rabin–Karp algorithm [4]. Moreover, some other software, such as MUMmer [5][6], uses data structures, such as suffix tree [7], suffix array [8], or FM-index [9], to find homologous segments. Recently, Minimap2 [10], which also adopts this strategy, is gaining popularity and is used as the basis of ViralMSA [11], which can perform multiple sequence alignment of viral genomes with the help of a reference sequence and is linearly scalable with the number of sequences. MAFFT [12] utilizes fast Fourier transform (FFT) to accelerate the calculation of the correlation between two sequences, which is an indicator of homologous regions of the sequences. These homologous regions can then act as anchors in pairwise sequence alignment. Additionally, it is concluded in Ref [12] that the accuracy of FFT-based methods is almost unaffected by this heuristic approach.
The concept of divide and conquer is also adopted in some multiple sequence alignment software to scale to large datasets, such as FAME [13] and FMAlign [14], which vertically divide the sequences using common seeds among the sequences, and MAGUS [15] and Super5 [16], which divide the sequences horizontally into subsets that are small enough to be aligned fast and accurately.

2. Bounded Dynamic Programming

Bounded dynamic programming [17] is based on a heuristic idea: if two sequences have close similarity, then the number of gaps inserted in the sequences during alignment will be relatively small. Therefore, the possible backtracking paths will be close to the diagonal of the dynamic programming matrix for similar sequences. The possible interval can be seen as a strip with certain width parallel to the diagonal (Figure 1B). The states located in the strip are calculated, while the others are ignored. The width of the strip reflects the trade-off between the alignment accuracy and time consumption: a wide strip means more states needed to be calculated, whereas a narrow strip means that more states could be ignored, which will, however, increase the possibility of missing the optimal path.
Several methods are available for determining the strip range. A basic idea is to use the shape-based division, but this does not fully consider the biological significance and is rarely used. A simple improvement of this method is to set a threshold to filter the states that could be ignored. If the score of one state in the dynamic programming plus the score for the transition from this state to the final state is greater than the threshold, then transitions from this state are allowed. However, this approach requires transition scores to be estimated and a threshold to be set. The transition scores can be conservatively estimated by its upper bound, and the threshold can be generally determined using the iterative method proposed in Ref [18].

3. Scoring System of Pairwise Sequence Alignment

The most critical factor for the quality of a pairwise sequence alignment is the scoring system. It is the basis of the sequence alignment, including multiple sequence alignment, because it determines the direction of the alignment and reflects its quality. Most types of the sequence alignment software aim to obtain good alignment by defining an explicit or implicit objective function for scoring and improving their ability to achieve high score by adjusting alignment strategy. The higher score an alignment can achieve, the higher researchers think its accuracy will be in the corresponding scoring system. As an example, a model and the corresponding scoring system for pairwise alignment of nucleotide sequences containing frameshifts and stop codons comprise the main feature of MACSE, a multiple sequence alignment tool that is specific to coding sequences and takes into account frameshifts and stop codons [19].
Generally, the score of a pairwise sequence alignment is the sum of the scores of all aligned pairs. For alignment of two protein sequences, for example, each pair of aligned sites is scored depending on whether a gap is involved, or, if no gaps are involved, whether the two aligned residues are matched or mismatched. When a gap is involved, a gap penalty, which is usually a negative score, is given. Additionally, the score for matched and mismatched amino acid residues is generally determined using a substitution matrix.
The most basic substitution matrix is based on whether the two residues are matched or not. More complex matrices also take into consideration the attributes of nucleotides or amino acid residues. For example, the score of conversion–transversion matrix reflects the difference between conversion and transversion frequency in natural mutations [20]. Protein sequences contain more types of residues than nucleic acid sequences, and therefore, the substitutions and the frequency involved are more complicated. Early amino acid substitution matrix is based on the properties and the codons of amino acids [21]. More recent amino acid substitution matrices rely on the analysis of the substitution frequency of a large number of homologous sequences [21] and aim to reflect the natural probability of substitutions among amino acids at certain evolutionary distances by giving conservative substitutions higher scores. Typical amino acid substitution matrices are percent accepted mutations (PAM) [21][22] and BLOcks SUbstitution matrix (BLOSUM) [23]. Although these matrices are widely adopted, there are also matrices designed for specific protein domain, such as GPCRtm, which is summarized from the transmembrane segments of the G-protein-coupled receptor (GPCR) rhodopsin family for the reason that it is not optimal to align sequences with marked compositional biases using the general-purpose matrices [24].
In addition to substitution matrices, gap penalty is also an important part of the scoring system. A simple rule is to assign a fixed negative score when a nucleotide or amino acid residue aligns with a gap. However, this scoring method has some intrinsic limitations, mainly because insertions and deletions (indels) are small-probability events, especially in nucleic acid sequences where indels can cause frameshifts and disrupt all subsequent codons. Once a gap is inserted in an alignment, adjacent gaps are more likely to occur compared with gaps inserted at a distance from the first gap. Therefore, almost all sequence alignment algorithms now use the gap penalty rule based on the number of the gaps successively inserted, and the most typical one is the affine penalty. No optimal solution is universally applicable for the gap penalty, which is referred to as a “black art” requiring constant trial of errors [25].

References

  1. Lipman, D.J.; Pearson, W.R. Rapid and Sensitive Protein Similarity Searches. Science 1985, 227, 1435–1441.
  2. Pearson, W.R.; Lipman, D.J. Improved tools for biological sequence comparison. Proc. Natl. Acad. Sci. USA 1988, 85, 2444–2448.
  3. Altschul, S.F.; Gish, W.; Miller, W.; Myers, E.W.; Lipman, D.J. Basic local alignment search tool. J. Mol. Biol. 1990, 215, 403–410.
  4. Karp, R.M.; Rabin, M.O. Efficient randomized pattern-matching algorithms. IBM J. Res. Dev. 1987, 31, 249–260.
  5. Delcher, A.L.; Kasif, S.; Fleischmann, R.D.; Peterson, J.; White, O.; Salzberg, S.L. Alignment of whole genomes. Nucleic Acids Res. 1999, 27, 2369–2376.
  6. Marçais, G.; Delcher, A.L.; Phillippy, A.; Coston, R.; Salzberg, S.; Zimin, A. MUMmer4: A fast and versatile genome alignment system. PLOS Comput. Biol. 2018, 14, e1005944.
  7. Weiner, P. Linear pattern matching algorithms. In Proceedings of the 14th Annual Symposium on Switching and Automata Theory (Swat 1973), Iowa City, IA, USA, 15–17 October 1973; pp. 1–11.
  8. Manber, U.; Myers, G. Suffix Arrays: A New Method for On-Line String Searches. SIAM J. Comput. 1993, 22, 935–948.
  9. Ferragina, P.; Manzini, G. Opportunistic data structures with applications. In Proceedings of the 41st Annual Symposium on Foundations of Computer Science, Redondo Beach, CA, USA, 12–14 November 2000; pp. 390–398.
  10. Li, H. Minimap2: Pairwise alignment for nucleotide sequences. Bioinformatics 2018, 34, 3094–3100.
  11. Moshiri, N. ViralMSA: Massively scalable reference-guided multiple sequence alignment of viral genomes. Bioinformatics 2021, 37, 714–716.
  12. Kazutaka, K.; Misakwa, K.; Kei-ichi, K.; Miyata, T. MAFFT: A novel method for rapid multiple sequence alignment based on fast Fourier transform. Nucleic Acids Res. 2002, 30, 3059–3066.
  13. Naznooshsadat, E.; Elham, P.; Ali, S.-Z.; Etminan, N.; Parvinnia, E.; Sharifi-Zarchi, A. FAME: Fast and memory efficient multiple sequences alignment tool through compatible chain of roots. Bioinformatics 2020, 36, 3662–3668.
  14. Liu, H.; Zou, Q.; Xu, Y. A novel fast multiple nucleotide sequence alignment method based on FM-index. Brief. Bioinform. 2022, 23, bbab519.
  15. Smirnov, V.; Warnow, T. MAGUS: Multiple sequence Alignment using Graph clUStering. Bioinformatics 2021, 37, 1666–1672.
  16. Edgar, R.C. MUSCLE v5 enables improved estimates of phylogenetic tree confidence by ensemble bootstrapping. bioRxiv 2021.
  17. Spouge, J.L. Speeding up Dynamic Programming Algorithms for Finding Optimal Lattice Paths. SIAM J. Appl. Math. 1989, 49, 1552–1566.
  18. Korf, R.E. Depth-first iterative-deepening: An optimal admissible tree search. Artif. Intell. 1985, 27, 97–109.
  19. Ranwez, V.; Harispe, S.; Delsuc, F.; Douzery, E.J.P. MACSE: Multiple Alignment of Coding SEquences Accounting for Frameshifts and Stop Codons. PLoS ONE 2011, 6, e22594.
  20. Li, W.-H.; Wu, C.I.; Luo, C.C. A new method for estimating synonymous and nonsynonymous rates of nucleotide substitution considering the relative likelihood of nucleotide and codon changes. Mol. Biol. Evol. 1985, 2, 150–174.
  21. Schwartz, R.M.; Dayhoff, M.O. Matrices for Detecting Distant Relationships. In Atlas of Protein Sequences; National Biomedical Research Foundation: Washington, DC, USA, 1978; pp. 353–359.
  22. Jones, D.T.; Taylor, W.R.; Thornton, J.M. The rapid generation of mutation data matrices from protein sequences. Comput. Appl. Biosci. 1992, 8, 275–282.
  23. Henikoff, S.; Henikoff, J.G. Amino acid substitution matrices from protein blocks. Proc. Natl. Acad. Sci. USA 1992, 89, 10915–10919.
  24. Ríos, S.; Fernandez, M.F.; Caltabiano, G.; Campillo, M.; Pardo, L.; Gonzalez, A. GPCRtm: An amino acid substitution matrix for the transmembrane region of class A G Protein-Coupled Receptors. BMC Bioinform. 2015, 16, 206.
  25. Vingron, M.; Waterman, M.S. Sequence alignment and penalty choice: Review of concepts, case studies and implications. J. Mol. Biol. 1994, 235, 1–12.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Computer Science, Theory & Methods
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Furong TANG
,
Jiannan Chao
,
Lei Xu
View Times: 875
Revisions: 2 times (View History)
Update Date: 22 Apr 2022
Table of Contents
    1000/1000
    Hot Most Recent
    ScholarVision Creations
    Feedback