Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Niraj Kumar Shukla
 -- 1413 2022-04-19 10:36:18 |
2 Adjust the reference format
Lindsay Dong
Meta information modification 1413 2022-04-20 03:46:12 |

Video Upload Options

Do you have a full video?
Send video materials Upload full video

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Shukla, N.; Mirjalili, S.; , . Hybrid Dragonfly Algorithm for Induction Motors Efficiency Optimization. Encyclopedia. Available online: https://encyclopedia.pub/entry/21922 (accessed on 27 April 2024).
Shukla N, Mirjalili S,  . Hybrid Dragonfly Algorithm for Induction Motors Efficiency Optimization. Encyclopedia. Available at: https://encyclopedia.pub/entry/21922. Accessed April 27, 2024.
Shukla, Niraj, Seyedali Mirjalili,  . "Hybrid Dragonfly Algorithm for Induction Motors Efficiency Optimization" Encyclopedia, https://encyclopedia.pub/entry/21922 (accessed April 27, 2024).
Shukla, N., Mirjalili, S., & , . (2022, April 19). Hybrid Dragonfly Algorithm for Induction Motors Efficiency Optimization. In Encyclopedia. https://encyclopedia.pub/entry/21922
Shukla, Niraj, et al. "Hybrid Dragonfly Algorithm for Induction Motors Efficiency Optimization." Encyclopedia. Web. 19 April, 2022.
Hybrid Dragonfly Algorithm for Induction Motors Efficiency Optimization
Edit
This entry is adapted from the peer-reviewed paper 10.3390/s22072594

Induction motors tend to have better efficiency on rated conditions, but at partial load conditions, when these motors operate on rated flux, they exhibit lower efficiency. In such conditions, when these motors operate for a long duration, a lot of electricity gets consumed by the motors, due to which the computational cost as well as the total running cost of industrial plant increases. Squirrel-cage induction motors are widely used in industries due to their low cost, robustness, easy maintenance, and good power/mass relation all through their life cycle. A significant amount of electrical energy is consumed due to the large count of operational units worldwide; hence, even an enhancement in minute efficiency can direct considerable contributions within revenue saving, global electricity consumption, and other environmental facts. Hybrid dragonfly algorithm is a model of induction motor drive is taken, in which the proportional integral (PI) controller is tuned. The optimal tuning of gains of a PI controller such as proportional gain and integral gain is conducted. The tuning procedure in the controller is performed in such a condition that the efficiency of the induction motor should be maximum. Moreover, the optimization concept relies on the development of a new hybrid algorithm, the so-called Scrounger Strikes Levy-based dragonfly algorithm (SL-DA), that hybridizes the concept of dragonfly algorithm (DA) and group search optimization (GSO). 

induction motor PI controller speed control dragonfly algorithm

1. Introduction

Nowadays, asynchronous motors are massively used in the process of industrial applications with the requirement of a larger performance. From the IM [1][2] discovery period, it is assumed as the actuator dominance with a constant speed tactic. Within several decades, this has been deployed in numerous industries as drivers or actuators for generating mechanical forces and motions. Every year in industries, the operational units of IM are increasing; hence, the enhancement of efficiency is a top priority for industries by minimizing the losses which will increase as a result of global conservation of energy. Some of the challenging characteristics of IM, specifically the cage IM over DC motor, are less cost, small inertia, less maintenance, high efficiency, simpler design, inherently self-starting, and absence of collector brush systems. However, there are some demerits in IM, which is complex in nature, including a multivariable mathematical model, nonlinearity, and intrinsically incompetent offering of flexible speed operation. The aforesaid issues can be solved by constructing the motor control operators with smart scalar and vector strategies.
The control approach has assumed that the reference magnetic flux [3][4] is stable and nearer to its rated level (λrnm) on behalf of larger dynamic performance in spite of operating points. The resultant outcome of such procedures has unacceptable energy efficiency, while the IM is assumed as under-loaded. Most of the research explorations have demonstrated that about 45% of IMs drive 40% of their rated load. To tackle this challenge, the auto-adjustment of flux has to be made online regarding the load torque for attaining the reduced power loss. Actually, the flux leakage value with unique optimal on every operating point is tracked by the efficiency optimization algorithm derived [5][6][7] and pertained it to controlled IM [8][9]. For optimizing the drive system’s efficiency, many techniques have been evolved in the literature. They are categorized generally into two major models: MBO and SAO.

The MBO has possessed some challenges, which is its larger sensitivity to parameter variations and the count of arithmetic operations contained within the loss model’s solution. The characterization of SAO in [10][11] is made by its parameter insensitivity. However, it poses some promising challenges such as very slow convergence and high torque ripples to the optimal operating point while distinguished over MBO. In such cases, it has a very large search space and thereby outcomes in large time in the quest for optimal operating conditions. In fact, the optimization algorithm in [12][13] may underestimate the optimal flux with no adaptation of real-time parameters’ mechanisms, which may as well direct the destabilization of the drive system and impact the problem of “motor stalling”, particularly in the existence of an immediate change in load torque. It should be noted that in the full operating region, there is a critical issue in the identification of IM parameters accurately [14][15][16] and simultaneously, even by using the IM parameter stacking algorithms. Over the last few years, researchers have been working on evolutionary algorithms [17] such as genetic algorithms (GA) and swarm-intelligence-based algorithms [18] such as PSO, GSO, DA, FF, and ACO for optimization purposes under different working environments. These meta-heuristic algorithms are very efficient and determine an accurate estimation of optimal solutions compared to conventional algorithms.

This framework has introduced a novel model to maximize the efficiency of induction motors. For this, the objective model is constructed using the speed-control induction motor drive with the tuning of the PI controller. In this PI controller, the optimal tuning of PI controllers such as proportional gain and integral gain is made by introducing a newly hybrid algorithm named SL-DA, which is the hybridization of DA and GSO. 

2. Hybrid Dragonfly Algorithm

Induction motors are considered the industries’ workhorse because of their efficiency, power/mass relation, low cost and quite maintenance-free operation in their life span. Nonetheless, the motors that work on low efficiency waste more energy, which in turns maximizes the operational cost. As for the consequence of a large count of operating units and large energy consumption, even a small rise in improvement of efficiency has had a considerable effect on operational cost and the whole energy consumption. To make this possible, this proposal aims to introduce a newly hybrid algorithm that hybridizes the concept of dragonfly algorithm (DA) and group search optimization (GSO). DA is a newly meta-heuristic optimization technique [19] that solves the single-objective, discrete, and multi-objective problems. GSO is the algorithm [20] that is inspired based on animal searching behavior, which solves the continuous optimization problems. Furthermore, for a large amount of numerical testing, Mirjalili suggested that DA executes in a better way as compared to GA and PSO [21]. Conventionally, in [22][23], the scholars used the key attributes of loss model control (LMC) as well as search control (SC) together for assessment and reproduction of optimal flux component of current (Ids), for optimal efficiency operation of IM. However, the model struggles with the performance rate when there is variation in the load profile. Hence, to make a solution for this, this proposal introduces a new contribution that keeps the (Ids) value constant and optimizes the current regulator by optimally tuning the proportional integral (PI) controller as depicted in Figure 1, by improving the PI controller parameters such as proportional gain and the integral gain as well. This optimal selection obviously paves way for the optimal efficiency operation of induction motors.
/media/item_content/202204/625f65429cb34sensors-22-02594-g001.png
Figure 1. Proposed efficiency optimization model of induction motors.

3. Model of AC Sensor-Less Speed Control of Induction Motor Drive

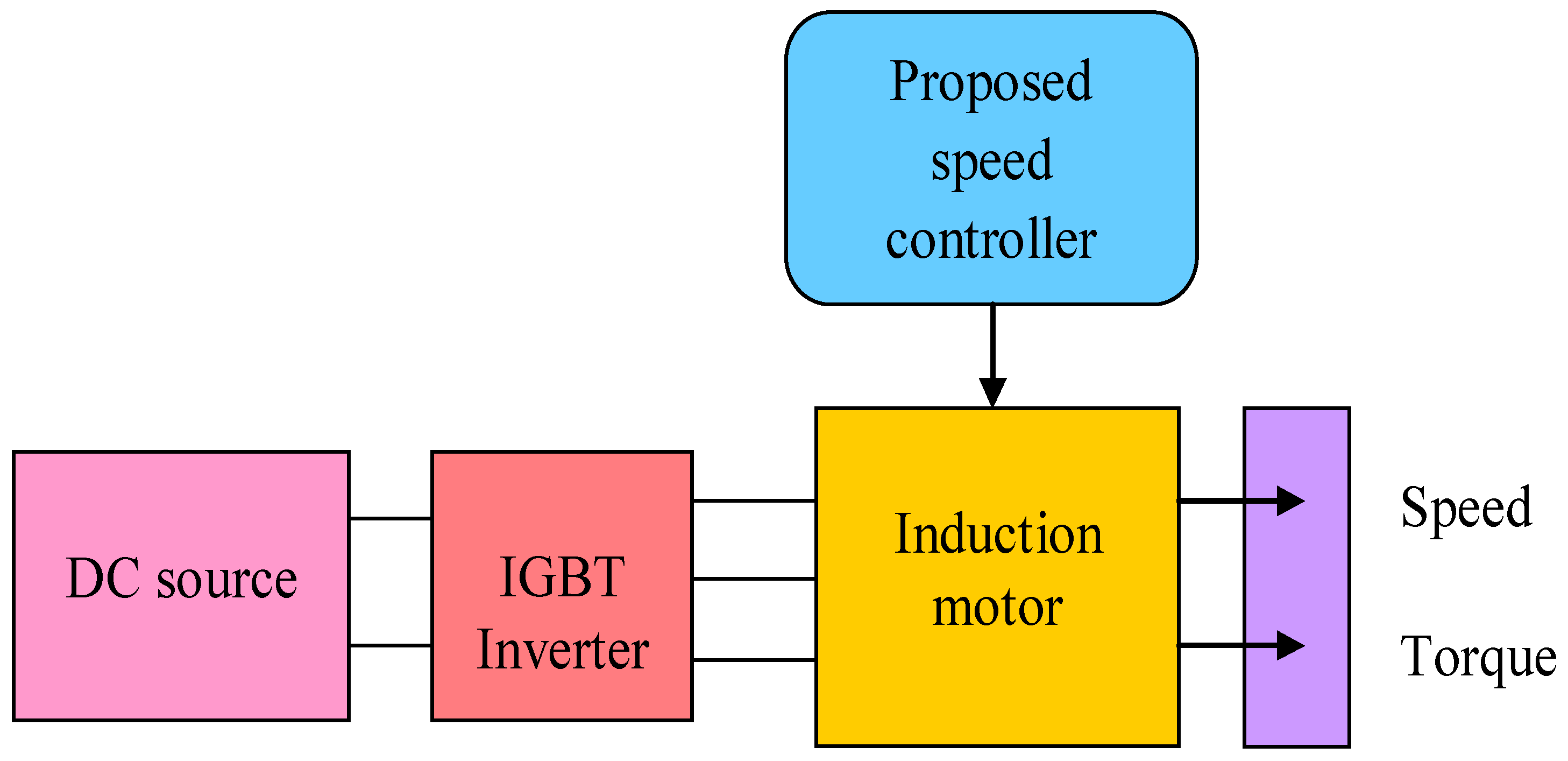
The system consists of a pure DC supply, which needs to be converted into AC by employing an Insulated Gate Bipolar Transistor (IGBT) inverter. An IGBT-based 3-phase inverter is used, which consists of twelve IGBT switches, out of which four IGBT switches per phase are arranged in an H-Bridge configuration. The scheme is depicted in Figure 2. A three-phase asynchronous machine is implemented within the asynchronous machine block, which is termed as single squirrel-cage, wound rotor, or double squirrel-cage. Here, the operation is made in motor mode where motor torque and speed are varied under different conditions. For the conventional method, IM uses the vector control technique where the voltage, current, and torque of a 3-phase induction motor are controlled by time-varying components. The speed is used as a feedback loop in a PI controller at different values of load torque. The proposed speed controller (AC) block exemplifies a PI speed regulator technique for AC machines that is utilized within vector-controlled drives. Here, two operating instances are present: the initial one is having both the outputs of torque as well as the flux references and the second has only the output of the torque reference. The speed of the machine is given in rpm as N; the speed reference of the machine is in rpm and is denoted as N∗. In this, the machine’s torque reference is termed as input, when the parameter of regulation type is fixed as torque. The flux reference is symbolized as Flux∗ and the unit of this is weber. The induction motor speed is controlled by tuning the PI controller; i.e., the proportional and integral gain of the PI controller is fine-tuned via a proposed SL-DA scheme.

/media/item_content/202204/625f654d260f5sensors-22-02594-g002.png
Figure 2. Representation of proposed model.

References

  1. Glowacz, A. Acoustic based fault diagnosis of three-phase induction motor. Appl. Acoust. 2018, 137, 82–89.
  2. Werner, U. Vibration control of large induction motors using actuators between motor feet and steel frame foundation. Mech. Syst. Signal Process. 2018, 112, 319–342.
  3. Ghosh, E.; Mollaeian, A.; Kim, S.; Tjong, J.; Kar, N.C. DNN-Based Predictive Magnetic Flux Reference for Harmonic Compensation Control in Magnetically Unbalanced Induction Motor. IEEE Trans. Magn. 2017, 53, 1–7.
  4. Castaldi, P.; Tilli, A. Parameter estimation of induction motor at standstill with magnetic flux monitoring. IEEE Trans. Control Syst. Technol. 2005, 13, 386–400.
  5. Liu, C.; Chau, K.T.; Li, W.; Yu, C. Efficiency Optimization of a Permanent-Magnet Hybrid Brushless Machine Using DC Field Current Control. IEEE Trans. Magn. 2009, 45, 4652–4655.
  6. Meng, L.; Dragicevic, T.; Vasquez, J.C.; Guerrero, J.M. Tertiary and Secondary Control Levels for Efficiency Optimization and System Damping in Droop Controlled DC–DC Converters. IEEE Trans. Smart Grid 2015, 6, 2615–2626.
  7. Nguyen-Trong, N.; Fumeaux, C. Tuning Range and Efficiency Optimization of a Frequency-Reconfigurable Patch Antenna. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 150–154.
  8. Bieler, G.; Marcelo, M.W. A magnetostrictive-fiber Bragg grating sensor for induction motor health monitoring. Measurement 2018, 122, 117–127.
  9. Adekitan, A.; Samuel, I.; Amuta, I.; AmutaElizabeth, E. Dataset on the performance of a three phase induction motor under balanced and unbalanced supply voltage conditions. Data Brief 2019, 24, 103947.
  10. Li, X.; Li, M. Multiobjective Local Search Algorithm-Based Decomposition for Multiobjective Permutation Flow Shop Scheduling Problem. IEEE Trans. Eng. Manag. 2015, 62, 544–557.
  11. Chen, B.; Zeng, W.; Lin, Y.; Zhang, D. A New Local Search-Based Multiobjective Optimization Algorithm. IEEE Trans. Evol. Comput. 2015, 19, 50–73.
  12. Bechikh, S.; Chaabani, A.; Ben Said, L. An Efficient Chemical Reaction Optimization Algorithm for Multiobjective Optimization. IEEE Trans. Cybern. 2015, 45, 2051–2064.
  13. Naji, H.R.; Sohrabi, M.; Rashedi, E. A High-Speed, Performance-Optimization Algorithm Based on a Gravitational Approach. Comput. Sci. Eng. 2012, 14, 56–62.
  14. Tamrakar, U.; Shrestha, D.; Malla, N.; Ni, Z.; Hansen, T.M.; Tamrakar, I.; Tonkoski, R. Comparative Analysis of Current Control Techniques to Support Virtual Inertia Applications. Appl. Sci. 2018, 8, 2695.
  15. Yetgin, A.G. Effects of induction motor end ring faults on motor performance. Experimental results. Eng. Fail. Anal. 2019, 96, 374–383.
  16. Bortoni, E.C.; Bernardes, J.V.; da Silva, P.V.V.; Faria, V.A.D.; Vieira, P.A.V. Evaluation of manufacturers strategies to obtain high-efficient induction motors. Sustain. Energy Technol. Assess. 2019, 31, 221–227.
  17. Ma, H. Model-Based Multiobjective Evolutionary Algorithm Optimization for HCCI Engines. IEEE Trans. Veh. Technol. 2015, 64, 4326–4331.
  18. Bujok, P.; Zamuda, A.; Das, S.; Suganthan, P.; Panigrahi, B. Cooperative Model of Evolutionary Algorithms and Real-World Problems. In Swarm, Evolutionary, and Memetic Computing and Fuzzy and Neural Computing; SEMCCO 2019, FANCCO 2019. Communications in Computer and Information Science; Springer: Cham, Switzerland, 2020; Volume 1092.
  19. Jafari, M.; Chaleshtari, M.H.B. Using dragonfly algorithm for optimization of orthotropic infinite plates with a quasi-triangular cut-out. Eur. J. Mech. A/Solids 2017, 66, 1–14.
  20. He, S.; Wu, Q.H.; Saunders, J.R. Group Search Optimizer: An Optimization Algorithm Inspired by Animal Searching Behavior. IEEE Trans. Evol. Comput. 2009, 13, 973–990.
  21. Wang, L.; Shi, R.; Dong, J. A Hybridization of Dragonfly Algorithm Optimization and Angle Modulation Mechanism for 0–1 Knapsack Problems. Entropy 2021, 23, 598.
  22. Choudhary, P.K.; Dubey, S.P.; Gupta, V.K. Efficiency optimization of induction motor drive at steady-state condition. In Proceedings of the International Conference on Control, Instrumentation, Communication and Computational Technologies (ICCICCT), Kumaracoil, India, 18–19 December 2015; pp. 470–475.
  23. Shukla, N.K.; Pandey, S.K.; Srivastava, R. Efficiency and Cost Optimization of Three-ϕ Induction Motor Using Soft Computing Techniques. In Computing Algorithms with Applications in Engineering, Algorithms for Intelligent Systems; Springer: Singapore, 2020; pp. 305–318.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Engineering, Electrical & Electronic
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Niraj Shukla
,
Seyedali Mirjalili
,
View Times: 330
Revisions: 2 times (View History)
Update Date: 26 Apr 2022
Table of Contents
    1000/1000
    Hot Most Recent
    Feedback