Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Niaz Muhammad Shahani
 + 2272 word(s) 2272 2022-03-23 09:57:58 |
2 update layout and reference
Rita Xu
 -258 word(s) 2014 2022-03-24 03:16:54 | |
3 update layout
Rita Xu
 + 1 word(s) 2015 2022-03-25 07:20:50 |

Video Upload Options

We provide professional Video Production Services to translate complex research into visually appealing presentations. Would you like to try it?
No, upload directly Yes

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Shahani, N. Elastic Modulus. Encyclopedia. Available online: https://encyclopedia.pub/entry/20926 (accessed on 21 December 2024).
Shahani N. Elastic Modulus. Encyclopedia. Available at: https://encyclopedia.pub/entry/20926. Accessed December 21, 2024.
Shahani, Niaz. "Elastic Modulus" Encyclopedia, https://encyclopedia.pub/entry/20926 (accessed December 21, 2024).
Shahani, N. (2022, March 23). Elastic Modulus. In Encyclopedia. https://encyclopedia.pub/entry/20926
Shahani, Niaz. "Elastic Modulus." Encyclopedia. Web. 23 March, 2022.
Elastic Modulus
Edit
This entry is adapted from the peer-reviewed paper 10.3390/su14063689

Elastic modulus (E) is a key parameter in predicting the ability of a material to withstand pressure and plays a critical role in the design of rock engineering projects. E has broad applications in the stability of structures in mining, petroleum, geotechnical engineering, etc. E can be determined directly by conducting laboratory tests, which are time consuming, and require high-quality core samples and costly modern instruments. Thus, devising an indirect estimation method of E has promising prospects.

elastic modulus K-fold cross-validation mining

1. Introduction

Elastic modulus (E) is a key parameter in predicting the ability of a material to withstand pressure and plays a critical role in the design process of rock-related projects. E has broad applications in the stability of structures in mining, petroleum, geotechnical engineering, etc. Accurate estimation of deformation properties of rocks, such as E, is very important for the design process of any underground rock excavation project. Intelligent indirect techniques for designing and excavating underground structures make use of a limited amount of data for design, saving time and money while ensuring the stability of the structures. This entry has economic and even social implications, which are integral elements of sustainability. Moreover, this entry aims to determine the stability of underground mine excavation, which may otherwise result in a disturbed overlying aquifer and earth surface profile, adversely affecting the environment. E provides insight into the magnitude and characteristics of the rock mass deformation due to changes in the stress field. Deformation and behavior of different types of rocks have been examined by different scholars [1][2][3][4]. Usually, there are two common methods, namely, direct (destructive) and indirect (non-destructive), to calculate the strength and deformation of rocks. Based on the principles suggested by ISRM (International Society for Rock Mechanics) and the ASTM (American Society for Testing Materials), direct evaluation of E in the laboratory is a complex, laborious, and costly process. Simultaneously, in the case of fragile, internally broken, thin, and highly foliated rocks, the preparation of a sample is very challenging [5]. Therefore, attention should be given to evaluate E indirectly by the use of rock index tests.
Several authors have developed prediction frameworks to overcome these limitations by using machine learning (ML)-based intelligent approaches such as multiple regression analysis (MRA), artificial neural network (ANN), and other ML methods [6][7][8][9][10][11][12][13][14][15][16][17][18][19][20][21]. Advances in ML have so far been driven by the development of new learning algorithms and theories, as well as by the continued explosion of online data and inexpensive computing [22]. Similarly, Waqas et al. used linear and nonlinear regression, regularization and ANFIS (using a neuro-fuzzy inference system) to predict the dynamic E of thermally treated sedimentary rocks [23]. Abdi et al. developed ANN and MRA (linear) models, including porosity (%), dry density (γd) (g/cm3), P-wave velocity (Vp) (km/s), and water absorption (Ab) (%) as input features to predict the rock E. According to their results, the ANN model showed high accuracy in predicting E compared to the MRA [10]. Ghasemi et al. evaluated the UCS and E of carbonate rocks by developing a model tree-based approach. According to their findings, the applied method revealed highly accurate results [24]. Shahani et al. developed a first-time XGBoost regression model in combination with MLR and ANN for predicting E of intact sedimentary rock and achieved high accuracy in their results [25]. Ceryan applied the minimax probability machine regression (MPMR), relevance vector machine (RVM), and generalized regression neural network (GRNN) models to predict the E of weathered igneous rocks [26]. Umrao et al. determined strength and E of heterogeneous sedimentary rocks using ANFIS based on porosity, Vp, and density. Thus, the proposed ANFIS models showed superb predictability [27]. Davarpanah et al. established robust correlations between static and dynamic deformation properties of different rock types by proposing linear and nonlinear relationships [28]. Aboutaleb et al. conducted non-destructive experiments with SRA (simple regression analysis), MRA, ANN, and SVR (support vector regression) and found that ANN and SVR models were more accurate in predicting dynamic E [29]. Mahmoud et al. employed an ANN model for predicting sandstone E. In that study, 409 datasets were used for training and 183 datasets were used for model testing. The established ANN model exposed highly accurate results (coefficient of determination (R2) = 0.999) and the lowest mean absolute percentage error ((AAPE) = 0.98) in predicting E [30]. Roy et al. used ANN, ANFIS, and multiple regression (MR) to predict the E of CO2 saturated coals. Thus, ANN and ANFIS outperformed the MR models [31]. Armaghani et al. predicted E of 45 main range granite samples by applying the ANFIS model in comparison with MRA and ANN. Based on their results, ANFIS proved to be an ideal model against MRA and ANN [32]. Singh et al. proposed an ANFIS framework for predicting E of rocks [33]. Köken predicted the deformation properties of rocks, i.e., tangential E (Eti) and tangential Poisson’s ratio (vti) of coal-bedded sandstones located in the Zonguldak Hard Coal Basin (ZHB), northwestern Turkey, using various statistical and soft computing methods such as different regression and ANN evaluations including the physicomechanical, mineralogical, and textural properties of the rocks. According to this analysis, the remarkable results were that the mineralogical characteristics of the rock have a significant influence on the deformation properties. In addition to comparative analysis, ANN was considered as a more effective tool than regression analysis in predicting Eti and vti of coal-bed sandstones [34]. Yesiloglu-Gultekin et al. used the different ML-based regression models such as NLMR, ANN, and ANFIS, and 137 datasets using unit weight, porosity, and sonic velocity to indirectly determine E of basalt. Based on the results and comparisons of various performance matrices such as R2, RMSE, VAF, and a20-index, ANN was successful in predicting E over NLMR and ANFIS [35]. Rashid et al. used non-destructive tests, i.e., MLR and ANN, to estimate the Q-factor and E for intact sandstone samples collected from the Salt Range region of Pakistan. The ANN model predicted Q-factor (R2 = 0.86) and E (R2 = 0.91) more accurately than MLR regression for Q-factor (R2 = 0.30) and E (R2 = 0.36) [36]. E was predicted using RF by Matin et al. For comparison, multivariate regression (MVR) and generalized regression neural network (GRNN) were used for the prediction of E. The input Vp-Rn was used for E. According to their results, RF yielded more satisfactory conclusions than MVR and GRNN [37]. Cao et al. used an extreme gradient boosting (XGBoost) integrated with the firefly algorithm (FA) model for predicting E. consequently, the proposed model was appropriate for predicting E [17]. Yang et al. developed the Bayesian model to predict the E of intact granite rocks; thus, the model performed with satisfactory predicted results [38]. Ren et al. developed several ML algorithms, namely, k-nearest neighbors (KNN), naive Bayes, RF, ANN, and SVM, to predict rock compressive strength by ANN and SVM with high accuracy [39]. Ge et al. determined rock joint shear failures using scanning and AI techniques. Thus, the developed SVM and BPNN were considered as sound determination methods [40]. Xu et al. developed several ML algorithms, namely, SVR, nearest neighbor regression (NNR), Bayesian ridge regression (BRR), RF, and gradient tree boosting regression (GTBR), to predict microparameters of rocks by RF with high accuracy [41].

2. Data Curation

In this research, 106 samples of soft sedimentary rocks, i.e., siltstone, claystone, and sandstone were collected from Block-IX of the Thar coalfield, as shown Figure 1, with the location map in the green. Then, the rock samples were prepared and partitioned according to the principles suggested by ISRM [42] and the ASTM [43] to maintain the same core size, and geological and geometric characteristics. In the laboratory of the Mining Engineering Department of Mehran University of Engineering and Technology (MUET), the experimental work was conducted on the studied rock samples to determine the physical and mechanical properties such as wet density (ρwet) in g/cm3, moisture (%), dry density (ρd) in g/cm3, Brazilian tensile strength (BTS) in (MPa), and elastic modulus (E) in (GPa). Figure 2 shows (a) collected core samples, (b) universal testing machine (UTM), (c) deformed core sample under compression for E test, and (d) deformed core sample for BTS test. The purpose of the UCS test was conducted on the standard core samples of NX size 54 mm in diameter with an applied load of 0.5 MPa/s using UTM according to the recommended ISRM standard to find the E of the rocks. Similarly, in order to find the tensile strength of the rock samples indirectly, the researchers performed the Brazilian test using UTM. Figure 3 illustrates the statistical distribution of the input features and output in the original dataset used in this study. In Figure 3, the legend of boxplots can be explained as: ▭ 25~75%, ⌶ Range within 1.5 IQR, ─ Median line, and ○ Outliers.
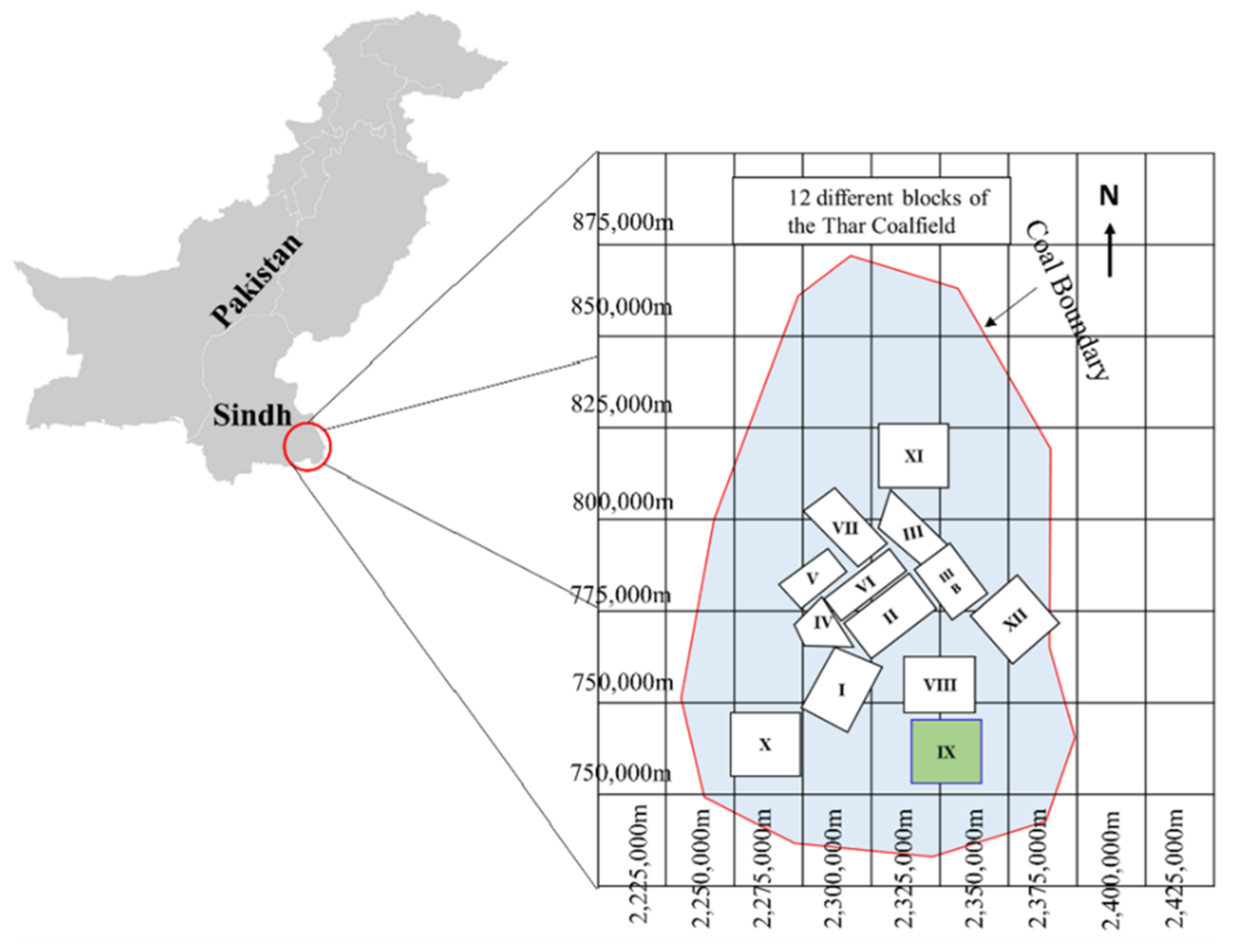
Sustainability 14 03689 g002
Figure 1. Location map of the study area.
Sustainability 14 03689 g003
Figure 2. (a) Rock core samples for test, (b) uniaxial testing machine, (c) deformed rock core specimen under compression, and (d) deformed core sample for BTS test.
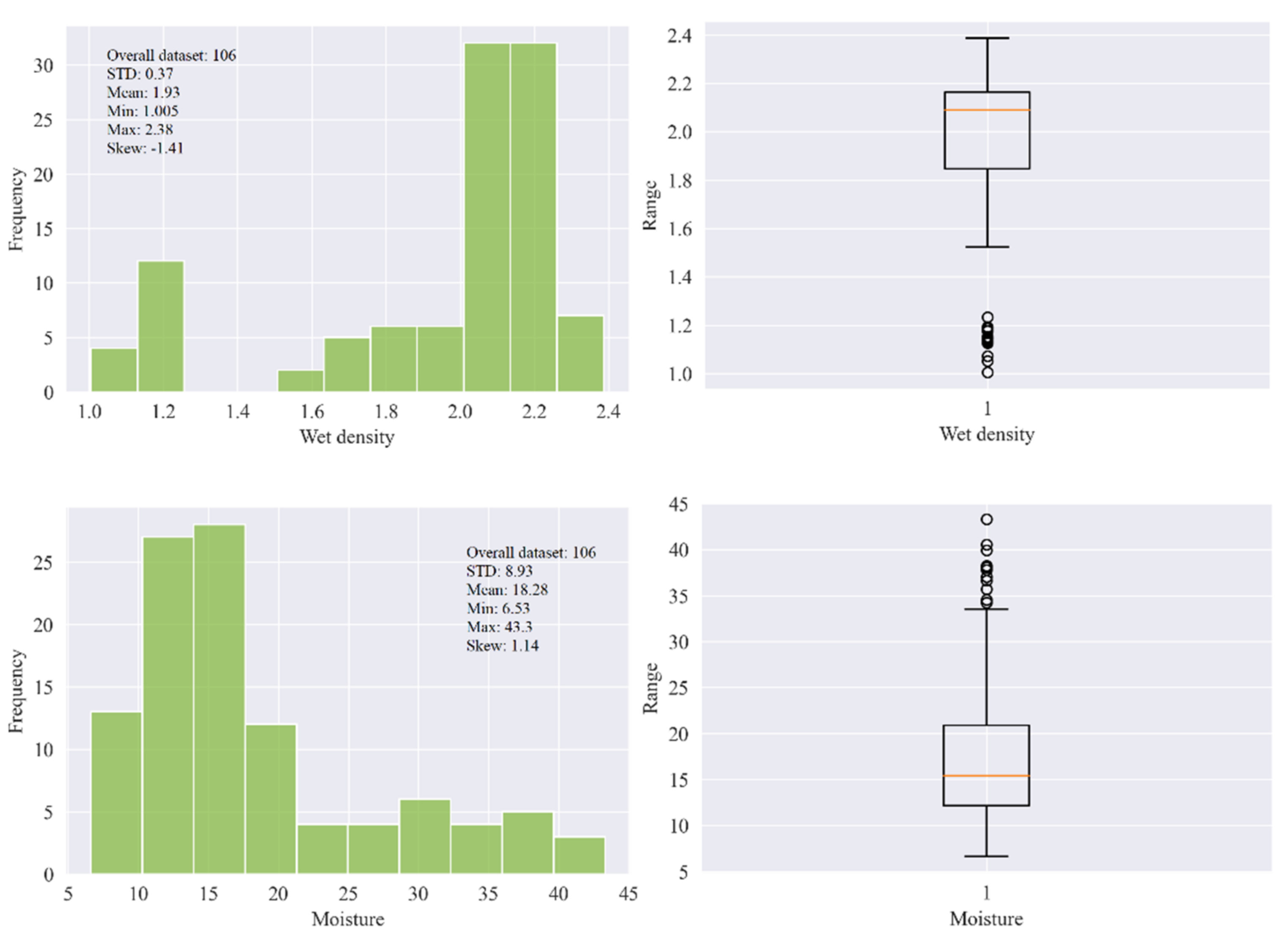
Sustainability 14 03689 g004a
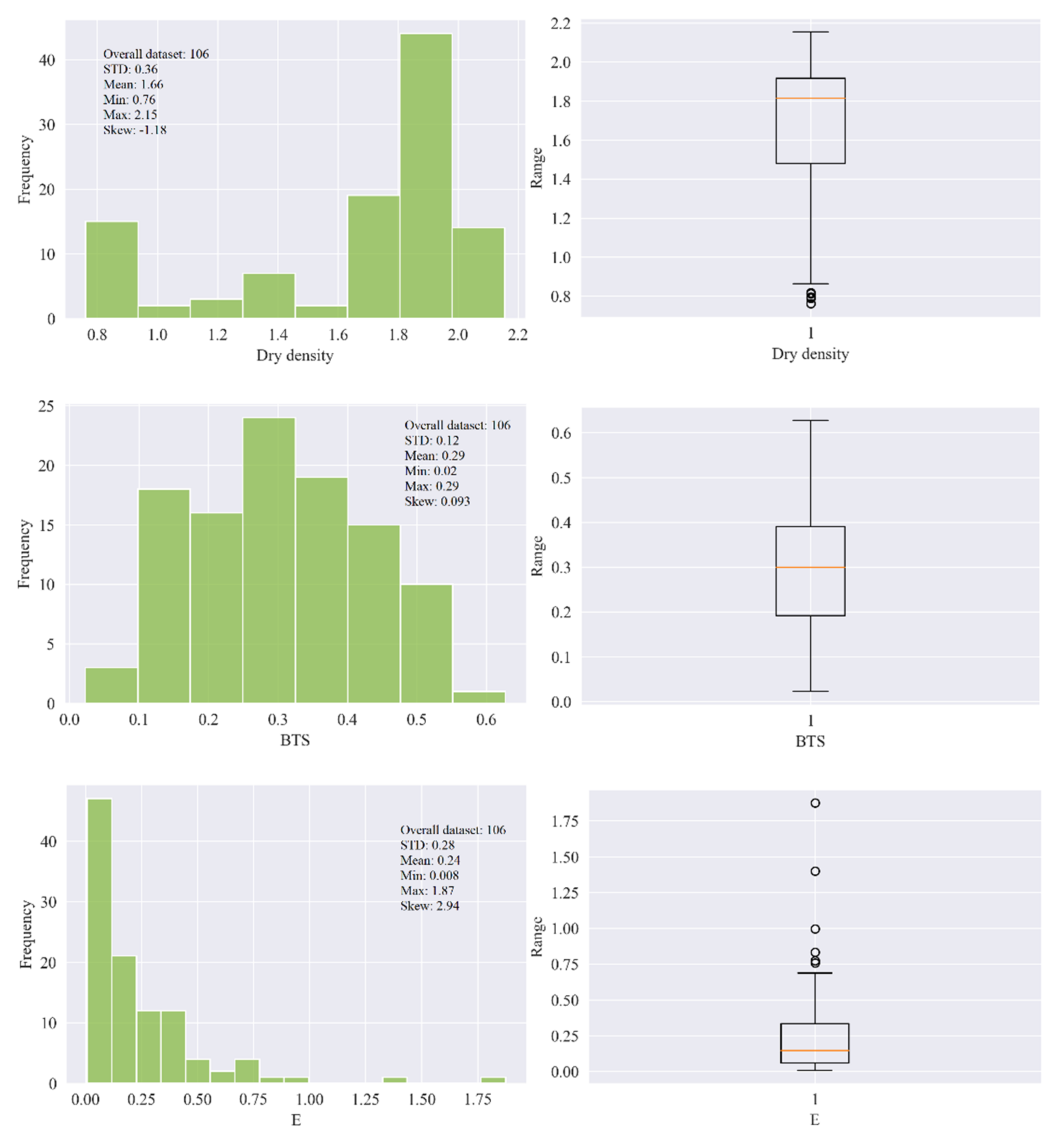
Sustainability 14 03689 g004b
Figure 3. The statistical distribution of the input features and output in the original dataset.
In order to visualize the original dataset of E, the seaborn module in Python was employed in this study, and Figure 4 demonstrates the pairwise correlation matrix and distribution of different input features and output E. It can be seen that BTS is moderately correlated to the E, whereas ρwet and ρd are negatively correlated to the E. Moisture representation does not correlate with E. It is worth mentioning that each feature cannot be well correlated with E independently, so all features are evaluated together to predict E.
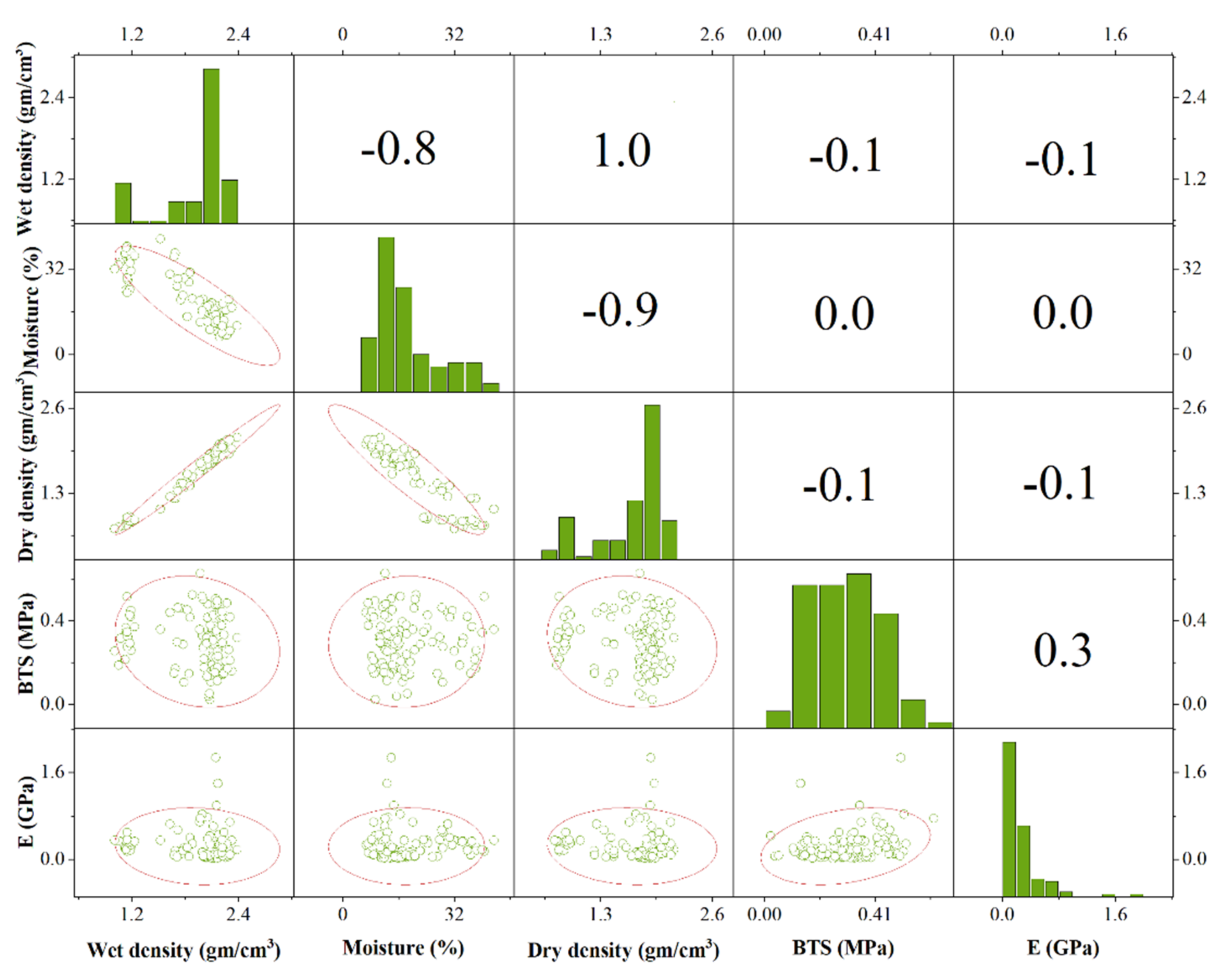
Sustainability 14 03689 g005
Figure 4. Pairwise correlation matrix and distribution of different input features and output E.

3. Developing ML-Based Intelligent Prediction Models

Light Gradient Boosting Machine

Light gradient boosting machine abbreviated as LightGBM, an open-source gradient boosting ML model from Microsoft, uses decision trees as the base training algorithm [44]. LightGBM puts continuous buckets of elemental values into separate bins with greater adeptness and a fast speed of training. It uses a histogram-based algorithm [45][46] to improve the learning phase, reduce consumption of memory, and integrate updated communication networks to enhance the regularity of training and is known as a parallel voting decision tree ML algorithm. The data for learning were partitioned into several trees, and local voting techniques were executed in each iteration to select top-k elements and gain globing voting techniques. As shown in Figure 5, LightGBM operates the leaf-wise approach to identify the leaf with the maximum splitter gain. LightGBM is best adopted for regression, classification, sorting, and several ML schemes. It builds a more complex tree than the level-wise distribution method through the leaf-wise distribution method, which can be considered as the main component of the execution algorithm with greater effectiveness. For all that, it can cause overfitting; however, by using the maximum depth element in LightGBM, it can be disabled.
Sustainability 14 03689 g006
Figure 5. The general structure of LightGBM.
LightGBM [44] is a widespread library for performing gradient boosting, with some modifications intended. The implementation of gradient boosting is mainly focused on algorithms for building a computational system. The library includes tenfold training hyperparameters to validate the implementation of the framework in different scenarios. The implementation of LightGBM also demonstrates advanced capabilities on CPUs and GPUs, which can work like gradient boosting with multifold integrations, comprising column randomization, bootstrap subsampling, and so on. The main features of LightGBM are gradient-based one-sided sampling and unique attribute bundling. Gradient-based one-sided sampling is a sub-sampling technique used to construct the base tree of learning data as an ensemble. In the AdaBoost ML algorithm, the purpose of this technique is to increase the significance of samples with greater likelihood that are connected with samples with higher gradients. When gradient-based one-sided sampling is executed, the base learner’s learning data are articulated based on the top portion of samples with greater gradients (a) plus the portion of arbitrary orders (b) recouped from samples with lower gradients. To compensate for changes in measurement propagation, samples from the lesser gradient class are organized together and weighted by (1 − x)/y, and at the same time, computing the data gain. In contrast, the unique attribute bundling technique accrues meager elements into an individual element. This can be ended in the absence of impeding any information when these elements do not contain a non-zero number of coincidences. Both mechanisms predict a gain in the complementary learning rate.

References

  1. Davarpanah, M.; Somodi, G.; Kovács, L.; Vásárhelyi, B. Complex analysis of uniaxial compressive tests of the Mórágy granitic rock formation (Hungary). Stud. Geotech. Mech. 2019, 41, 21–32.
  2. Xiong, L.X.; Xu, Z.Y.; Li, T.B.; Zhang, Y. Bonded-particle discrete element modeling of mechanical behaviors of interlayered rock mass under loading and unloading conditions. Geomech. Geophys. Geo-Energy Geo-Resour. 2019, 5, 1–16.
  3. Rahimi, R.; Nygaard, R. Effect of rock strength variation on the estimated borehole breakout using shear failure criteria. Geomech. Geophys. Geo-Energy Geo-Resour. 2008, 4, 369–382.
  4. Zhao, Y.S.; Wan, Z.J.; Feng, Z.J.; Xu, Z.H.; Liang, W.G. Evolution of mechanical properties of granite at high temperature and high pressure. Geomech. Geophys. Geo-Energy Geo-Resour. 2017, 3, 199–210.
  5. Jing, H.; Rad, H.N.; Hasanipanah, M.; Armaghani, D.J.; Qasem, S.N. Design and implementation of a new tuned hybrid intelligent model to predict the uniaxial compressive strength of the rock using SFS-ANFIS. Eng. Comput. 2021, 37, 2717–2734.
  6. Lindquist, E.S.; Goodman, R.E. Strength and deformation properties of a physical model melange. In Proceedings of the 1st North American Rock Mechanics Symposium, Austin, TX, USA, 1–3 June 1994; Nelson, P.P., Laubach, S.E., Eds.; Balkema: Rotterdam, The Netherlands, 1994.
  7. Singh, T.N.; Dubey, R.K. A study of transmission velocity of primary wave (P-Wave) in Coal Measures sandstone. J. Sci. Ind. Res. 2000, 59, 482–486.
  8. Tiryaki, B. Predicting intact rock strength for mechanical excavation using multivariate statistics, artificial neural networks and regression trees. Eng. Geol. 2008, 99, 51–60.
  9. Ozcelik, Y.; Bayram, F.; Yasitli, N.E. Prediction of engineering properties of rocks from microscopic data. Arab. J. Geosci. 2013, 6, 3651–3668.
  10. Abdi, Y.; Garavand, A.T.; Sahamieh, R.Z. Prediction of strength parameters of sedimentary rocks using artificial neural networks and regression analysis. Arab. J. Geosci. 2018, 11, 587.
  11. Teymen, A.; Mengüç, E.C. Comparative evaluation of different statistical tools for the prediction of uniaxial compressive strength of rocks. Int. J. Min. Sci. Technol. 2020, 30, 785–797.
  12. Li, C.; Zhou, J.; Armaghani, D.J.; Li, X. Stability analysis of underground mine hard rock pillars via combination of finite difference methods, neural networks, and Monte Carlo simulation techniques. Undergr. Space 2021, 6, 379–395.
  13. Momeni, E.; Yarivand, A.; Dowlatshahi, M.B.; Armaghani, D.J. An efficient optimal neural network based on gravitational search algorithm in predicting the deformation of geogrid-reinforced soil structures. Transp. Geotech. 2021, 26, 100446.
  14. Parsajoo, M.; Armaghani, D.J.; Mohammed, A.S.; Khari, M.; Jahandari, S. Tensile strength prediction of rock material using non-destructive tests: A comparative intelligent study. Transp. Geotech. 2021, 31, 100652.
  15. Armaghani, D.J.; Harandizadeh, H.; Momeni, E.; Maizir, H.; Zhou, J. An optimized system of GMDH-ANFIS predictive model by ICA for estimating pile bearing capacity. Artif. Intell. Rev. 2021, 55, 2313–2350.
  16. Harandizadeh, H.; Armaghani, D.J. Prediction of air-overpressure induced by blasting using an ANFIS-PNN model optimized by GA. Appl. Soft Comput. 2021, 99, 106904.
  17. Cao, J.; Gao, J.; Rad, H.N.; Mohammed, A.S.; Hasanipanah, M.; Zhou, J. A novel systematic and evolved approach based on XGBoost-firefly algorithm to predict Young’s modulus and unconfined compressive strength of rock. Eng. Comput. 2021, 1–17.
  18. Yang, F.; Li, Z.; Wang, Q.; Jiang, B.; Yan, B.; Zhang, P.; Xu, W.; Dong, C.; Liaw, P.K. Cluster-formula-embedded machine learning for design of multicomponent β-Ti alloys with low Young’s modulus. npj Comput. Mater. 2020, 6, 1–11.
  19. Duan, J.; Asteris, P.G.; Nguyen, H.; Bui, X.N.; Moayedi, H. A novel artificial intelligence technique to predict compressive strength of recycled aggregate concrete using ICA-XGBoost model. Eng. Comput. 2020, 37, 3329–3346.
  20. Pham, B.T.; Nguyen, M.D.; Nguyen-Thoi, T.; Ho, L.S.; Koopialipoor, M.; Quoc, N.K.; Armaghani, D.J.; Van Le, H. A novel approach for classification of soils based on laboratory tests using Adaboost, Tree and ANN modeling. Transp. Geotech. 2021, 27, 100508.
  21. Asteris, P.G.; Mamou, A.; Hajihassani, M.; Hasanipanah, M.; Koopialipoor, M.; Le, T.T.; Kardani, N.; Armaghani, D.J. Soft computing based closed form equations correlating L and N-type Schmidt hammer rebound numbers of rocks. Transp. Geotech. 2021, 29, 100588.
  22. Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260.
  23. Waqas, U.; Ahmed, M.F. Prediction Modeling for the Estimation of Dynamic Elastic Young’s Modulus of Thermally Treated Sedimentary Rocks Using Linear–Nonlinear Regression Analysis, Regularization, and ANFIS. Rock Mech. Rock Eng. 2020, 53, 5411–5428.
  24. Ghasemi, E.; Kalhori, H.; Bagherpour, R.; Yagiz, S. Model tree approach for predicting uniaxial compressive strength and Young’s modulus of carbonate rocks. Bull. Eng. Geol. Environ. 2018, 77, 331–343.
  25. Shahani, N.M.; Zheng, X.; Liu, C.; Hassan, F.U.; Li, P. Developing an XGBoost Regression Model for Predicting Young’s Modulus of Intact Sedimentary Rocks for the Stability of Surface and Subsurface Structures. Front. Earth Sci. 2021, 9, 761990.
  26. Ceryan, N. Prediction of Young’s modulus of weathered igneous rocks using GRNN, RVM, and MPMR models with a new index. J. Mt. Sci. 2021, 18, 233–251.
  27. Umrao, R.K.; Sharma, L.K.; Singh, R.; Singh, T.N. Determination of strength and modulus of elasticity of heterogenous sedimentary rocks: An ANFIS predictive technique. Measurement 2018, 126, 194–201.
  28. Davarpanah, S.M.; Ván, P.; Vásárhelyi, B. Investigation of the relationship between dynamic and static deformation moduli of rocks. Geomech. Geophys. Geo-Energy Geo-Resour. 2020, 6, 29.
  29. Aboutaleb, S.; Behnia, M.; Bagherpour, R.; Bluekian, B. Using non-destructive tests for estimating uniaxial compressive strength and static Young’s modulus of carbonate rocks via some modeling techniques. Bull. Eng. Geol. Environ. 2018, 77, 1717–1728.
  30. Mahmoud, A.A.; Elkatatny, S.; Ali, A.; Moussa, T. Estimation of static young’s modulus for sandstone formation using artificial neural networks. Energies 2019, 12, 2125.
  31. Roy, D.G.; Singh, T.N. Regression and soft computing models to estimate young’s modulus of CO2 saturated coals. Measurement 2018, 129, 91–101.
  32. Armaghani, D.J.; Mohamad, E.T.; Momeni, E.; Narayanasamy, M.S. An adaptive neuro-fuzzy inference system for predicting unconfined compressive strength and Young’s modulus: A study on Main Range granite. Bull. Eng. Geol. Environ. 2015, 74, 1301–1319.
  33. Singh, R.; Kainthola, A.; Singh, T.N. Estimation of elastic constant of rocks using an ANFIS approach. Appl. Soft Comput. 2012, 12, 40–45.
  34. Köken, E. Assessment of Deformation Properties of Coal Measure Sandstones through Regression Analyses and Artificial Neural Networks. Arch. Min. Sci. 2021, 66, 523–542.
  35. Yesiloglu-Gultekin, N.; Gokceoglu, C. A Comparison Among Some Non-linear Prediction Tools on Indirect Determination of Uniaxial Compressive Strength and Modulus of Elasticity of Basalt. J. Nondestruct. Eval. 2022, 41, 10.
  36. Awais Rashid, H.M.; Ghazzali, M.; Waqas, U.; Malik, A.A.; Abubakar, M.Z. Artificial Intelligence-Based Modeling for the Estimation of Q-Factor and Elastic Young’s Modulus of Sandstones Deteriorated by a Wetting-Drying Cyclic Process. Arch. Min. Sci. 2021, 66, 635–658.
  37. Matin, S.S.; Farahzadi, L.; Makaremi, S.; Chelgani, S.C.; Sattari, G. Variable selection and prediction of uniaxial compressive strength and modulus of elasticity by random forest. Appl. Soft Comput. 2018, 70, 980–987.
  38. Yang, L.; Feng, X.; Sun, Y. Predicting the Young’s Modulus of granites using the Bayesian model selection approach. Bull. Eng. Geol. Environ. 2019, 78, 3413–3423.
  39. Ren, Q.; Wang, G.; Li, M.; Han, S. Prediction of rock compressive strength using machine learning algorithms based on spectrum analysis of geological hammer. Geotech. Geol. Eng. 2019, 37, 475–489.
  40. Ge, Y.; Xie, Z.; Tang, H.; Du, B.; Cao, B. Determination of the shear failure areas of rock joints using a laser scanning technique and artificial intelligence algorithms. Eng. Geol. 2021, 293, 106320.
  41. Xu, C.; Liu, X.; Wang, E.; Wang, S. Calibration of the microparameters of rock specimens by using various machine learning algorithms. Int. J. Geomech. 2021, 21, 04021060.
  42. Brown, E.T. Rock Characterization Testing & Monitoring—ISRM Suggested Methods, ISRM—International Society for Rock Mechanics; Pergamon Press: London, UK, 2007; Volume 211.
  43. D4543-85; Standard Practices for Preparing Rock Core as Cylindrical Test Specimens and Verifying Conformance to Dimensional and Shape Tolerances. ASTM—American Society for Tenting and Materials: West Conshohocken, PA, USA, 2013.
  44. Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. Lightgbm: A highly efficient gradient boosting decision tree. Adv. Neural Inf. Process. Syst. 2017, 30, 3146–3154.
  45. Zeng, H.; Yang, C.; Zhang, H.; Wu, Z.H.; Zhang, M.; Dai, G.J.; Babiloni, F.; Kong, W.Z. A lightGBM-based EEG analysis method for driver mental states classification. Comput. Intell. Neurosci. 2019, 2019, 3761203.
  46. Liang, W.; Luo, S.; Zhao, G.; Wu, H. Predicting hard rock pillar stability using GBDT, XGBoost, and LightGBM algorithms. Mathematics 2020, 8, 765.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Area Studies
Contributor MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Niaz Shahani
View Times: 1.4K
Revisions: 3 times (View History)
Update Date: 25 Mar 2022
Table of Contents
    1000/1000
    Hot Most Recent
    Video Production Service
    Feedback