You're using an outdated browser. Please upgrade to a modern browser for the best experience.
Principles of NMR and MRI
Edit
This entry is adapted from the peer-reviewed paper 10.3390/pharmaceutics14020382

Depending on the appropriately tuned amplifiers and transceiver coils, in theory, any nuclear magnetic resonance (NMR) active nucleus can be used for imaging by MRI. A nucleus with a spin quantum number of ½ (e.g., 1H, 3He, 13C, 14N, 15N, 19F, 19O, 31P, etc.) is designated to be in two spin states and the direction of spin alignment depends on the sign (+/−) of the gyromagnetic ratio, one of the two spin states will align along the magnetic field (ground state, lower energy), whereas the other one will align against it (excited state, higher energy). When an external magnetic field is applied, the spins in the ground state can be promoted to the excited state after absorbing the energy. Upon the termination of the external magnetic field, the spin returns to its equilibrium state (ground state) by a process called relaxation. There are two processes involved, each with an exponential time constant (Ti, i = 1,2): ‘T1’ (longitudinal or spin-lattice) or ‘T2’ (transverse or spin-spin) relaxation times. These parameters help in determining the signal/contrast-to-noise ratio (SNR) and the image resolution.

magnetic resonance imaging nuclear magnetic resonace perfluorocarbons Gadolinium based contrast agents

1. Gadolinium Based Contrast Agents (GBCAs)

GBCAs are paramagnetic coordination complexes comprising of a Gadolinium-III (Gd(III)/Gd3+) ion and a chelator that independently do not emit MR signals but can bring about a significant reduction of the T1 of nearby water protons [1]. Annually, millions of patients globally undergo MRI scans who receive GBCAs. The lanthanides like Gd are highly coveted CAs due to their intrinsic paramagnetic properties, favorable relaxation time, [2], and stable shelf life. GBCAs permit the imaging of tissues that are less sensitive to motion (hence better quality images) and higher throughput by shortening T1 of the proton [1]. The contrast enhancement function comes from Gd3+ that has seven unpaired electrons. After administering the CA, the diagnostic image is procured while the patient is in the scanner. Generally, the diagnostic and prognostic information attained from MRI predominates the information given from other techniques. Several GBCAs have gained regulatory approvals, including Eovist® (gadoxetate disodium), Omniscan® (a gadodiamide), Gadavist® (gadobutrol), Optimark® (gadoversetamide), etc. [3][4]. The free Gd3+ ion is toxic since its ionic radius is relatively close to zinc, calcium, or iron [5]. Likely interference with calcium ion channels in the living entity is plausible. Gd3+, therefore, needs to be cocooned within chelator (most often used is organic ligands) to avoid those toxicity issues [6][7]. Two classes of chelates developed to complex Gd: linear or macrocyclic organic ligands evade the release of free Gd3+ and make the resulting complexes kinetically and thermodynamically stable [8].
However, in 2006, GBCAs were associated with a devastating and potentially fatal condition called nephrogenic systemic fibrosis [9], recurrently reported in patients suffering from renal deficiency, and its onset can occur months after the last GBCA administration [1]. Furthermore, it is prevailing that some fraction of the residual Gd3+ can remain in the body for long periods, although the chemical form or its whole-body distribution is still obscure [1]. Because of the low sensitivity of MRI, formulation stipulates a high concentration of Gd3+, typically 0.1 mmol kg−1 body weight (approximately 0.5 M aqueous solution) that is hypertonic relative to body fluids [10]. Notwithstanding this, some macrocyclic GBCAs are still sanctioned and can be administered to the patients but in the lowest possible doses. Together, these conclusions have led to renewed interest in finding alternatives to using Gd3+ for MR contrast [11][12]. Further, in 2017, the European medicines agency (EMA) and FDA confirmed the necessity of restricting the use of some linear GBCAs because they tend to release Gd ions in the biological environment [13][14]. For a deeper understanding of GBCAs, the reader is referred to the following reviews [15][1][7][12].

2. Fluorine as a Contrast Agent

There is variation among different elements of an NMR active nucleus for their relative natural abundance and response to a magnetic field, meaning that the NMR signal per mole of the compound varies from element to element [16]. Choosing an imaging nucleus from the different NMR active elements depends on its properties entailing to its inherent physical, chemical, and biological properties. In 1977, shortly after the invention of 1H MRI, Holland et al. [17], have demonstrated the feasibility of fluorine-19 suited for fluorine-MRI (19F MRI), which paved the way for new research avenues in molecular and cellular imaging. 19F MRI is anticipated to be a promising imaging tool in the future due to unambiguous detection, acceptable in vivo acquisition times, and relatively high spatial resolution [18]. The external addition of a suitable fluorinated compound (also called a probe/tracer/label) is a prerequisite for 19F MRI/magnetic resonance spectroscopy (MRS).
Only insignificant amounts of endogenous fluorine are embedded in the teeth and bone matrix of the human body. This immobilized fluorine (<10–6 M) has only a very short T2 relaxation as they are in the solid-state and cannot be detected by 19F MRI (that is below the detection limit), which extinguishes the possibility of intrinsic background signals, implying potentially high SNR [19]. Using the same scanner and the receiver electronics of 1HMRI with retuned radiofrequency coils/dual-tuned coils, 19F-images can be superimposed on anatomical, high-resolution 1H images, generating hotspot 19F-images (hybrid 1H/19F MRI) [20][21][22]. The MR effect of the additional element (19F here) does not disturb the local magnetic field either and adds a second colored layer of complementary information to the corresponding grayscale 1H image, hence called “hot spot” [23][24]. Aside from that, 19F is a natural halogen, non-radioactive stable isotope of fluorine [25], unlike the radioactive isotope 18F used in PET imaging [26], and thus it is not necessary to have advanced synthetic skills to introduce fluorine into a probe.

3. Similarity between Fluorine and Hydrogen

19F exhibits the NMR phenomenon like 1H, which has one unpaired proton and no unpaired neutrons, and thus with a net spin of ½. Many fluorinated compounds that are non-toxic and chemically inert provide a non-invasive means to study biological systems. When an NMR-active nucleus is placed in an external magnetic field of strength B, it can absorb a photon of frequency ν that depends on the gyromagnetic ratio (γ) of the particle.
In Equation (1), B is the strength of the applied magnetic field (in Tesla [T]), and γ is the gyromagnetic ratio of the nucleus (in MHzT−1). The similarity of 19F’s gyromagnetic ratio to 1H is another strong suit that makes 19F the second most sensitive stable nuclei for MRI followed by 1H (Table 1) [27][28]. At 3T, the typical field strength for clinical MRI scanners, ν is 128 MHz for 1H and 120 MHz for 19F [10]. These frequencies (commonly known as ‘resonance frequencies’) lie in the radiofrequency (RF) range, and hence, MRI signals are RF signals. 19F resonates at a resonant frequency of 94% that of 1H [29]. A huge advantage of MRI over other imaging methods is that RF pulse is non-ionizing radiation and per se can penetrate deep into soft tissues [30]. Once the wave packet of frequency (in this case RF pulse) is applied, as already disclosed, the ground state spins obtain the energy to transition to the excited state, whose energy can be posited by Equation (2)
where h is Planck’s constant (6.626 × 10−34 joules (J)-second (S)). Denoting the population of the ground state as NG and that of the excited state as NE, the MR signal intensity is proportional to the population excess between the two states that can be secured by Equation (3) [10]
At thermal equilibrium, the distribution of spins between the two states obeys Boltzmann’s law. The population ratio, which is the ratio between the spins in the excited state to the ground state, (NE/NG), is obtained by Equation (4) which is 0.9999802 for 1H and 0.9999814 for 19F [10].
where ∆ϵ is the energy difference between the excited and ground state, k the Boltzmann constant (1.381 × 10−23 JK−1), and T, the absolute temperature in kelvin (K). Hence, the MR signal is the output of a tiny population difference between the two states as only 9–10 spins out of almost 10 lakhs contribute to the sequel. It sums to the fact that in the absence of CAs, MRI is an intrinsically low-sensitive technique. NMR receptivity is the absolute NMR sensitivity of a nucleus at its natural abundance [16]. 1H has the most distinguished receptivity of any nucleus. To identify an absolute value of receptivity for other nuclei, it is represented relative to 1H, with 1H having a receptivity of 1. 19F atom with a natural abundance of 100%, has a receptivity of 0.834 relative to 1H, and the fact that it is not a particularly rare (or expensive) element [27] makes it exemplary suitor for replacing 1H. It has a relative sensitivity of 83% compared to 1H and is essentially devoid in biological tissues [27]. Table 1 compares the properties of hydrogen and fluorine that present a large extent of similarity between them except for the chemical shift, for which fluorine is electron-rich, so possesses a high chemical shift.
Table 1. Comparative properties between hydrogen and fluorine.
Table
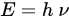
Parameter 1H 19F
Natural abundance (%) 99.98 100
Spin 1/2 1/2
Gyromagnetic ratio (γ) in MHz/T 42.576 40.076
Relative sensitivity 1.0 0.834
Van de Waals’ radius (in Å) 1.2 (H–C) 1.35 (F–C)
The population ratio (NE/NG) 0.9999802 0.9999814
∆ϵ/kT at 3T 1.98 × 10−5 1.86 × 10−5
Lattice spacing 4.97 Å
(Hydrocarbon)		 5.9 Å
(fluorocarbon)
Chemical shifts in ppm (NMR) 0 to 15 >350

References

  1. Wahsner, J.; Gale, E.M.; Rodriguez-Rodriguez, A.; Caravan, P. Chemistry of MRI Contrast Agents: Current Challenges and New Frontiers. Chem. Rev. 2019, 119, 957–1057.
  2. Xiao, Y.D.; Paudel, R.; Liu, J.; Ma, C.; Zhang, Z.S.; Zhou, S.K. MRI contrast agents: Classification and application (Review). Int. J. Mol. Med. 2016, 38, 1319–1326.
  3. Index to Drug-Specific Information. Available online: https://www.fda.gov/drugs/postmarket-drug-safety-information-patients-and-providers/index-drug-specific-information (accessed on 2 January 2022).
  4. Lohrke, J.; Frenzel, T.; Endrikat, J.; Alves, F.C.; Grist, T.M.; Law, M.; Lee, J.M.; Leiner, T.; Li, K.C.; Nikolaou, K.; et al. 25 Years of Contrast-Enhanced MRI: Developments, Current Challenges and Future Perspectives. Adv. Ther. 2016, 33, 1–28.
  5. Idee, J.M.; Port, M.; Raynal, I.; Schaefer, M.; Le Greneur, S.; Corot, C. Clinical and biological consequences of transmetallation induced by contrast agents for magnetic resonance imaging: A review. Fundam. Clin. Pharmacol. 2006, 20, 563–576.
  6. Stockman, J.A. Oral Prednisolone for Preschool Children with Acute Virus-Induced Wheezing. Yearb. Pediatr. 2010, 2010, 515–518.
  7. De León-Rodríguez, L.M.; Martins, A.F.; Pinho, M.C.; Rofsky, N.M.; Sherry, A.D. Basic MR relaxation mechanisms and contrast agent design. J. Magn. Reson. Imaging 2015, 42, 545–565.
  8. Hequet, E.; Henoumont, C.; Djouana Kenfack, V.; Lemaur, V.; Lazzaroni, R.; Boutry, S.; Vander Elst, L.; Muller, R.N.; Laurent, S. Design, Characterization and Molecular Modeling of New Fluorinated Paramagnetic Contrast Agents for Dual 1H/19F MRI. Magnetochemistry 2020, 6, 8.
  9. Grobner, T. Gadolinium--a specific trigger for the development of nephrogenic fibrosing dermopathy and nephrogenic systemic fibrosis? Nephrol. Dial. Transplant. 2006, 21, 1104–1108.
  10. Yu, Y.B. Fluorinated dendrimers as imaging agents for 19F MRI. Wiley Interdiscip. Rev. Nanomed. Nanobiotechnol. 2013, 5, 646–661.
  11. FDA Gadolinium Retention after Gadolinium Based Contrast Magnetic Resonance Imaging in Patients with Normal Renal Function; U.S. Food and Drug Administration: Silver Spring, MD, USA, 2017; pp. 127–131.
  12. Do, C.; DeAguero, J.; Brearley, A.; Trejo, X.; Howard, T.; Escobar, G.P.; Wagner, B. Gadolinium-Based Contrast Agent Use, Their Safety, and Practice Evolution. Kidney360 2020, 1, 561–568.
  13. Dekkers, I.A.; Roos, R.; van der Molen, A.J. Gadolinium retention after administration of contrast agents based on linear chelators and the recommendations of the European Medicines Agency. Eur. Radiol. 2018, 28, 1579–1584.
  14. FDA. FDA Drug Safety Communication: FDA. In Warns that Gadolinium-Based Contrast Agents (GBCAs) are Retained in the Body; Requires New Class Warnings; FDA: Silver Spring, MR, USA, 2017.
  15. Hao, D.; Ai, T.; Goerner, F.; Hu, X.; Runge, V.M.; Tweedle, M. MRI contrast agents: Basic chemistry and safety. J. Magn. Reson. Imaging 2012, 36, 1060–1071.
  16. Knight, J.C.; Edwards, P.G.; Paisey, S.J. Fluorinated contrast agents for magnetic resonance imaging; a review of recent developments. RSC Adv. 2011, 1.
  17. Holland, G.N.; Bottomley, P.A.; Hinshaw, W.S. 19F magnetic resonance imaging. J. Magn. Reson. Imaging 1977, 28, 133–136.
  18. Weise, G.; Basse-Luesebrink, T.C.; Wessig, C.; Jakob, P.M.; Stoll, G. In vivo imaging of inflammation in the peripheral nervous system by 19F MRI. Exp. Neurol. 2011, 229, 494–501.
  19. Tirotta, I.; Dichiarante, V.; Pigliacelli, C.; Cavallo, G.; Terraneo, G.; Bombelli, F.B.; Metrangolo, P.; Resnati, G. 19F magnetic resonance imaging (MRI): From design of materials to clinical applications. Chem. Rev. 2015, 115, 1106–1129.
  20. Otake, Y.; Soutome, Y.; Hirata, K.; Ochi, H.; Bito, Y. Double-tuned radiofrequency coil for 19F and 1H imaging. Magn. Reson. Med. Sci. 2014, 13, 199–205.
  21. Keupp, J.; Rahmer, J.; Grasslin, I.; Mazurkewitz, P.C.; Schaeffter, T.; Lanza, G.M.; Wickline, S.A.; Caruthers, S.D. Simultaneous dual-nuclei imaging for motion corrected detection and quantification of 19F imaging agents. Magn. Reson. Med. 2011, 66, 1116–1122.
  22. Wolters, M.; Mohades, S.G.; Hackeng, T.M.; Post, M.J.; Kooi, M.E.; Backes, W.H. Clinical Perspectives of Hybrid Proton-Fluorine Magnetic Resonance Imaging and Spectroscopy. Investig. Radiol. 2013, 48, 341–350.
  23. Bouvain, P.; Temme, S.; Flogel, U. Hot spot 19 F magnetic resonance imaging of inflammation. Wiley Interdiscip. Rev. Nanomed. Nanobiotechnol. 2020, 12, e1639.
  24. Liu, W.; Frank, J.A. Detection and quantification of magnetically labeled cells by cellular MRI. Eur. J. Radiol. 2009, 70, 258–264.
  25. Grapentin, C.; Barnert, S.; Schubert, R. Monitoring the Stability of Perfluorocarbon Nanoemulsions by Cryo-TEM Image Analysis and Dynamic Light Scattering. PLoS ONE 2015, 10, e0130674.
  26. Vatsadze, S.Z.; Eremina, O.E.; Veselova, I.A.; Kalmykov, S.N.; Nenajdenko, V.G. 18F-Labelled catecholamine type radiopharmaceuticals in the diagnosis of neurodegenerative diseases and neuroendocrine tumours: Approaches to synthesis and development prospects. Russ. Chem. Rev. 2018, 87, 350–373.
  27. Harris, R.K.; Becker, E.D.; de Menezes, C.; Sonia, M.; Goodfellow, R.; Granger, P. NMR nomenclature. Nuclear spin properties and conventions for chemical shifts (IUPAC Recommendations 2001). Pure Appl. Chem. 2001, 73, 1795–1818.
  28. Schmieder, A.H.; Caruthers, S.D.; Keupp, J.; Wickline, S.A.; Lanza, G.M. Recent Advances in 19Fluorine Magnetic Resonance Imaging with Perfluorocarbon Emulsions. Engineering 2015, 1, 475–489.
  29. Ruiz-Cabello, J.; Barnett, B.P.; Bottomley, P.A.; Bulte, J.W. Fluorine 19F MRS and MRI in biomedicine. NMR Biomed. 2011, 24, 114–129.
  30. Kissane, J.; Neutze, J.A.; Singh, H. Radiology Fundamentals, Introduction to Imaging & Technology, 6th ed.; Springer: Cham, Switzerland, 2020; 431p.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Biochemistry & Molecular Biology
Contributor MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Joice Maria Joseph
View Times: 789
Revisions: 2 times (View History)
Update Date: 18 Feb 2022
Table of Contents
Academic Video Service
Feedback