
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Richard de Grijs | + 2849 word(s) | 2849 | 2021-11-22 09:11:27 | | | |
| 2 | Amina Yu | + 81 word(s) | 2930 | 2022-01-11 03:14:59 | | | | |
| 3 | Amina Yu | + 81 word(s) | 2930 | 2022-01-11 03:17:32 | | | | |
| 4 | Richard de Grijs | Meta information modification | 2930 | 2022-01-11 03:18:03 | | | | |
| 5 | Amina Yu | -104 word(s) | 2826 | 2022-01-11 04:50:44 | | | | |
| 6 | Amina Yu | + 30 word(s) | 2856 | 2022-01-12 02:37:18 | | |
Video Upload Options
Chromospheric (magnetic) activity is evidence of the presence of strong and variable magnetic fields. Magnetically active chromospheres are predominantly found in cool stars with convective envelopes of spectral types F and later. Day- to year-long variability is associated with the evolution and rotational modulation of individual magnetically active regions.
1. Introduction
In solar-type stars, the innermost atmospheric layer, the photosphere, is located just above the surface convection zone. At larger radii, the next main solar atmospheric zone is the chromosphere (‘sphere of colour’), covering altitudes of approximately 3000–5000 km and extending through a region of partial hydrogen ionisation.
Almost all luminous stars, except for white dwarfs, feature chromospheres of some sort, although they are usually most prominent and magnetically active in lower main-sequence stars and brown dwarfs of F and later spectral types, as well as in giant and subgiant stars.
Chromospheres exhibit temperature inversion. The temperature of the solar chromosphere initially cools down from the Sun’s surface temperature (5770–5780 K) to approximately 3840 K. It then rapidly increases to temperatures in excess of 35,000 K at the onset of the solar atmospheric transition region, which extends to the corona[1][2]. Heating of the chromosphere to temperatures above the level required to maintain radiative equilibrium is driven by a combination of mechanical heating (pulsations and shocks), acoustic heating (pulsation-driven sound waves causing hydrodynamic shocks), magnetic fields (Alfvén waves, i.e., transverse or torsional magnetohydrodynamic waves), turbulence and ambipolar diffusion[3][4][5][6][7][8], and references therein)—i.e., separation of oppositely charged species in a plasma owing to the effects of the ambient electric field.
In the solar chromosphere magnetic heating causes the temperature to increase to a plateau of approximately 7000 K, with the ambient density falling by orders of magnitude with respect to the region near the photosphere[9][10]. The 7000 K plateau results from a balance between magnetic heating and radiative cooling through collisionally excited Hα, Ca II K and Mg II k radiation. The intensity of the latter lines scales with the level of non-thermal heating in the chromosphere, so that they are useful proxies for both the strength of the underlying magnetic field and the area covered by that field.
At its base, the chromosphere is homogeneous, although numerous filaments and ‘spicules’ extend up to altitudes of several ×104 km. Some even reach up to some 150,000 km in the form of the solar prominences (filaments viewed side-on) associated with coronal mass ejections. Both filaments and spicules—as well as their horizontal counterparts, known as ‘fibrils’—are plumes and tendrils of luminous gas. Their presence reflects the importance of magnetic activity, e.g., organised in the form of magnetic flux tubes[11] .
Chromospheric (magnetic) activity is related to photometric and spectroscopic variability on a range of timescales. Day- to year-long variability is associated with the evolution and rotational modulation of individual magnetically active regions. That is, stellar rotation is intricately correlated with chromospheric activity, as well as with stellar age. In fact, stellar rotation—particularly differential rotation—is responsible for the conversion of undisturbed poloidal magnetic fields into twisted toroidal fields (e.g., [12]).
Magnetic activity is likely triggered by the interplay of rotation and turbulent convection at the stellar surface. In turn, this triggers cyclic and self-sustained global stellar magnetic activity, including the well-known 11-year solar sunspot activity cycle [13][14]. Direct solar observations have been performed since approximately 1609. The wealth of observational data has allowed us to explore the significant variability of the Sun’s cycle-averaged magnetic activity level in great detail. The latter ranges from the extremely quiet ‘Maunder Minimum’ (1645–1715), when photospheric sunspots almost completely disappeared, to the present-day enhanced magnetic activity.
With increasing stellar age, the strength of the surface magnetic field—and, hence, a star’s magnetic activity—decreases in response to magnetic braking of a star’s rotation rate through angular momentum losses induced by magnetised winds and structural variations [15][16]. As such, quantification of a star’s chromospheric magnetic activity offers a direct stellar age measurement[14][17][18][19][20][21][22][23][24]. In addition, chromospheric activity relates the changes observed at the stellar surface to changes occurring deeper into the stellar interior [25], in particular for stars exhibiting solar-like dynamos ([26][27], and references therein). Hence, its study can shed light on the physical mechanisms responsible for these changes[28] [29] and thus better constrain dynamo models[30][31] .
Finally, magnetically active stars tend to exhibit flares or superflares (sudden releases of magnetic energy)[32], often large and rapidly evolving starspots (cooler regions where convection is suppressed by strong magnetic fields)[33][34][35][36][37], as well as faculae and plages (unusually bright regions in the photosphere and chromosphere, respectively)[38][39]. Dark starspots and bright faculae are usually located in stellar photospheres, whereas plages tend to be associated with chromospheres [39].
2. Magnetic Activity Cycles and the Solar Dynamo
The Sun is a magnetically moderately active star exhibiting short- to long-term fluctuations. The Sun’s magnetic nature drives solar activity (i.e., solar flares, coronal mass ejections, high-speed solar winds and solar energetic particles) and, in particular, the presence and appearance of sunspots. The appearance of sunspots can be attributed to deep-seated toroidal flux ropes which rise through the Sun’s convective envelope and reach the photosphere. Whereas the stability and the rise of toroidal flux ropes are fairly well-understood[40], the process through which the diffuse, large-scale solar magnetic field produces concentrated toroidal flux ropes which will subsequently give rise to sunspots remains poorly understood.
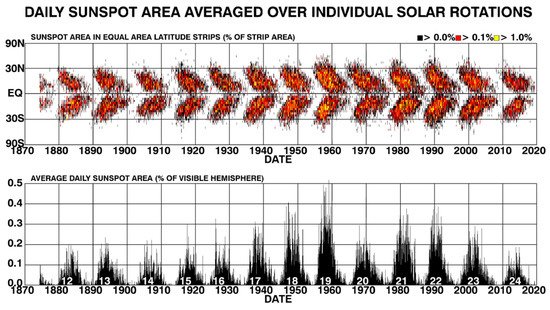
The complex sunspot cycle can be expressed using a sunspot ‘butterfly diagram’ (see Figure 1), which shows the fractional coverage of sunspots as a function of solar latitude and time (see the reviews by [41][42] and references therein). In addition, assuming that the toroidal fluxes, which likely govern the appearance of sunspots, rise radially and are formed where the magnetic field is strongest, the sunspot butterfly diagram also reflects a spatio-temporal ‘map’ of the Sun’s internal, large-scale toroidal magnetic-field component.
Dynamo theory proposes that stars, including our Sun, possess physical mechanisms that generate a magnetic field. Figure 2 provides a schematic overview of the basic features of the solar dynamo. To fully understand solar (stellar) dynamo theory we have to consider the key ingredients through which a convecting, rotating and electrically conducting fluid can maintain a magnetic field over cosmic timescales. These ingredients include the turbulent motions present in convective regions or, in some cases, also in radiative zones [43]. Convection is an instability that occurs in a stratified fluid or plasma, which in turn leads to the transportation of energy through the bulk displacement of parcels of ‘fluid’. In stellar convection zones, convection carries most of the energy.

Figure 2. Schematic of the solar hydromagnetic dynamo. The dashed lines outline the Sun’s photosphere and the base of the convection zone, known as the ‘tachocline’. The colours show the rate of rotation within the Sun, with differential rotation occurring in the convection zone. (© Paul Higgins, 2012. doi:10.6084/m9.figshare.102094.v1. Reproduced under a Creative Commons Attribution 4.0 International License; https://creativecommons.org/licenses/by/4.0.)
In the solar cycle context, we care about identifying the circumstances under which the flow fields observed and/or inferred in the Sun can sustain the cyclic regeneration of the magnetic field associated with the observed solar cycle.
3. Diagnostics
One of the most frequently used indicators of chromospheric activity in cool early-F to M-type stars is the occurrence of non-thermal flux reversal in the cores of the Ca II H and K absorption lines. Ca II H and K ions originate in both the upper photosphere and the chromosphere; they are often associated with the presence of plages [45]and are sensitive to magnetic activity [46].
Although analyses of carefully selected spectral-line characteristics are preferred to obtain the highest-quality physical parameters of chromospherically active stars, integrated quantities such as bolometric flux-normalised indices [47][48], equivalent widths [49][50][ and absolute chromospheric fluxes are often employed instead.
The physical interpretation of integrated quantities is not straightforward, given that these measures are not true reflections of chromospheric radiative losses [51]. Nevertheless, the Mt Wilson chromospheric activity index, SMW, is the most commonly employed chromospheric activity diagnostic[52][53][54][55] . It is derived by measuring the chromospheric Ca II H and K line fluxes, normalised to the nearby continuum:
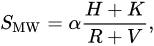
where H and K are the line fluxes measured in 1.09 Å-wide triangular bandpasses (full width at half maximum), whereas R and V represent estimates of the ‘pseudo-continuum’ on either side of the lines, measured in 20 Å-wide spectral windows; α is a normalisation constant [53][56][57].
The SMW index requires a correction for line blanketing, i.e., the contribution from photospheric flux in the line cores. We also need to normalise the star’s bolometric luminosity. The index resulting from having applied the latter corrections is known as RHK [48][56],

where σ is the Stefan–Boltzmann constant.
Perhaps the most important diagnostic relationship allowing us to probe the physics of stars exhibiting chromospheric activity is the chromospheric activity–age relation. Until recently, it was thought that chromospheric activity declines smoothly, rapidly and monotonically with increasing age[18][22] for ages up to about 1.5 Gyr[21][23], beyond which any activity would cease.
The physical mechanism thought responsible for this behaviour is the notion that stars lose mass through coronal winds, which in turn leads to a reduction in angular momentum as well as in the torque acting on the stellar surface. In combination, these effects lead to a gradual decrease in the stellar rotation rate on million-year timescales. Thus, the extent of braking owing to the decreasing stellar rotation is directly related to a reduced efficiency in the generation and amplification of magnetic fields at the base of the convection zone[13][24]. Consequently, a reduction in chromospheric heating follows [48]. Observationally, this will lead to a decrease in the chromospheric flux in the cores of the diagnostic absorption lines as a function of increasing stellar age.
However, Lorenzo-Oliveira et al. [14][24] have challenged this paradigm. They showed, based on observations of G dwarfs in old open clusters as well as a sample of 82 solar twins, that the smooth, monotonic decrease in activity extended with high significance (characterised by a false-alarm probability of just 1%) to ages of at least 6–7 Gyr for solar-mass, solar-metallicity stars aged 0.6–9 Gyr[17][18][22][58][59].
4. Chromospheric Activity across the Hertzsprung–Russell Diagram
Cool FGK-type main-sequence stars other than the Sun also routinely exhibit magnetic activity cycles[37]. However, unlike the long-term solar cycle, cool stellar magnetic activity can be categorised into three distinct types, including solar-like cyclic activity, highly variable non-cyclic activity and flat activity [60].
F-type stars are characterised by very thin outer convection zones. As a consequence, they exhibit irregular variability rather than proper stellar cycles [61][62][63][64]. This may imply that the physical mechanism at the basis of this type of stellar variability differs from that driving longer-term stellar cycles [28][29].
G- and K-type stars, including the Sun, tend to exhibit secondary, shorter-term cycles [54][65][66][67][68][69], which may be manifestations of a second stellar dynamo in addition to that responsible for the main stellar (and solar) cycles. It has been suggested that such secondary dynamos might be evidence of polarity-reversing solar(-like) activity cycles [70].
Chromospheric and coronal activity in evolved late-type stars remain poorly understood. Although the chromospheres in these highly evolved stars appear to be much cooler than the solar chromosphere, it has been suggested that the level of chromospheric emission remains at a basal level[71][72][73]. The ‘basal’ flux is equivalent to the low chromospheric activity boundary[74][75][76][77][78][79]. Chromospheric heating at these late evolutionary stages could be either due to magnetic fields or caused by pulsations or wave action ([71], and references therein); the precise mechanism is as yet unresolved [80].
Uchida & Bappu ([81] and references therein) have investigated the renewal of chromospheric activity in red giants and supergiants. These studies have revealed a likely reappearance of dynamo activity in the stellar interior which arises due to the core spin-up. This core spin-up is thought to be driven by the core contraction that occurs during the star’s evolution off the main sequence to the giant stage.
Chromospheres in fully convective M dwarfs are significantly more compressed, and hence characterised by higher densities, than in solar-type stars. Given these higher densities, Balmer-line cooling in M dwarfs is more efficient than in solar-type chromospheres, and Hα is the principal diagnostic line [82]. It is as yet unclear how M-dwarf chromospheres are heated.
L-dwarf chromospheres are cooler and have smaller filling factors [82]. X-ray, Hα, Lyman continuum and radio emission observations of at least some brown dwarfs, particularly of types earlier than mid-L, show evidence of the presence of higher-temperature regions reminiscent of chromospheres or hot coronae in their upper atmospheres[83][84][82][85][86][87][88][89][90][91]. The implied boundary at mid-L brown dwarf types may be real and might be associated with the threshold for core hydrogen burning [92], with chromospheric activity—as traced by the ratios of the X-ray and Hα luminosities to the bolometric luminosity—decreasing towards later types[83][90] [93].
5. Close Binarity and Stellar Chromospheric Activity
Rapidly rotating evolved binary systems with close, tidally locked and cool components tend to be strongly magnetically active. They may, hence, exhibit chromospheric activity, e.g., in the form of Hα emission.
RS CVn systems are binary systems containing an F- to K-type giant or subgiant primary star. They feature active chromospheres—as traced by strong Ca II H and K emission—and large photospheric starspots. The latter may cover as much as 50% of the stellar surface [94][95][96]. The secondary components are G–M-type subgiants or dwarfs. They tend to be located well inside the systems’ Roche lobes. As such, these systems are close binaries which are (close to) tidally locked.
Magnetic activity similar to that seen for the Sun, in the form of strong optical flares, was first discovered on red dwarf stars of types K–M, that is, lower main-sequence stars with masses ranging from the core hydrogen-burning limit at 0.08 M⊙ to 0.5 M⊙ for M0-type stars[96] . Such red dwarf stars are now known after their prototype, UV Ceti. In binary systems involving red dwarf stars, periodic brightness variations of up to ΔV∼0.5 mag (although amplitudes of 0.1 mag are more usual; [96]), were first noticed as out-of-eclipse light-curve distortions. Starspots covering up to 10% of the stellar surface as a possible cause of those distortions, combined with rotational modulation, were first proposed by Kron[97] [98] (see also[99][100][101] ).
Composed of a red dwarf and a G- or K-type component, BY Dra objects—70% of which are close binary systems [102]—are among the most chromospherically active objects. They exhibit strong Ca II H and K emission out of eclipse. Spectroscopically, BY Dra systems closely resemble RS CVn systems. They can be distinguished on the basis of their luminosities, however. BY Dra systems are systematically fainter than RS CVn binaries. BY Dra light curves exhibit periods close to the systems’ rotation periods, 1–5 days [102], although the brightness variations are usually irregular between successive periods. In essence, therefore, BY Dra systems exhibit quasi-sinusoidal variability owing to rotational modulation combined with slow changes in their mean brightness caused by changes in the distribution of the spotted regions [103].
W UMa systems are low-mass, ‘overcontact’ binaries, where both solar-type components have completely filled their Roche lobes, mass transfer from the larger, more massive component to the smaller, less massive component is ongoing, and both components are tidally synchronised. As such, W UMa components share a common convective envelope. Both components of W UMa systems are characterised by rapid rotation.
They exhibit continuous light-curve variability. Approximately 0.1% of the F–K-type dwarfs in the solar neighbourhood are W UMa systems [104]; they comprise 95% of eclipsing binaries in our local volume in the Milky Way [105]. These systems are most likely formed through nuclear evolution of the most massive component in the detached phase or through angular-momentum evolution within the convective envelope[106].
An increasing body of evidence, including from Doppler imaging[107][108][109], supports the notion that W UMa systems, and in particular the primary components, exhibit strong magnetic activity in the form of starspots (covering both components; [96], and references therein), flares, strong chromospheres and coronae [110]. In turn, this suggests that these systems are subject to strong angular momentum loss and (relatively weak) magnetic braking by magnetised winds ([111], and references therein). In strongly magnetised objects like W UMa systems, stellar winds are released along the coronal magnetic field lines, which have their origin in the stellar surface convection zones.
A fourth type of rapidly rotating [96], tidally locked, semi-detached eclipsing binary systems featuring magnetic activity comprises the so-called Algol-type systems. Algols are composed of a hot, B–F-type main-sequence primary component and a cooler, less massive G–K-type subgiant secondary, which both tend to rotate synchronously with their orbital periods. The cooler component is usually characterised by a deep convective envelope that fills the star’s Roche lobe; the hotter star’s Roche lobe is not filled. Combined with their rapid rotation, these boundary conditions give rise to the occurrence of starspots and other evidence of magnetic activity [112]on the secondary component, similarly to RS CVn, BY Dra and W UMa systems.
Chromospheric activity—manifested in the form of starspots and flares—is observed through Hα and Ca II H and K emission, although not necessarily strong emission[113][114][115]. Since starspots only cover the cool stellar component, they can only be observed (e.g., by means of Doppler tomography) during primary total eclipses. This thus only gives us access to a single hemisphere of the cool component.
References
- Dupree, A.K.; Lobel, A.; Young, P.R.; Ake, T.B.; Linsky, J.L.; Redfield, S. A Far-Ultraviolet Spectroscopic Survey of Luminous Cool Stars. Astrophys. J. 2005, 622, 629–652. [Google Scholar] [CrossRef]
- Dupree, A.K.; Li, T.Q.; Smith, G.H. Hubble Space Telescope Observations of Chromospheres in Metal-Deficient Field Giants. Astron. J. 2007, 134, 1348–1359. [Google Scholar] [CrossRef]
- Spitzer, L. Physics of Fully Ionized Gases, 2nd ed.; Interscience: New York, NY, USA, 1962. [Google Scholar]
- Khomenko, E.; Collados, M.; Díaz, A.; Vitas, N. Fluid description of multi-component solar partially ionized plasma. Phys. Plasmas 2014, 21, 092901. [Google Scholar] [CrossRef]
- Ballester, J.L.; Alexeev, I.; Collados, M.; Downes, T.; Pfaff, R.F.; Gilbert, H.; Khodachenko, M.; Khomenko, E.; Shaikhislamov, I.F.; Soler, R.; et al. Partially Ionized Plasmas in Astrophysics. Space Sci. Rev. 2018, 214, 58. [Google Scholar] [CrossRef]
- Cally, P.S.; Khomenko, E. Fast-to-Alfvén Mode Conversion and Ambipolar Heating in Structured Media. I. Simplified Cold Plasma Model. Astrophys. J. 2019, 885, 58. [Google Scholar] [CrossRef]
- González-Morales, P.A.; Khomenko, E.; Vitas, N.; Collados, M. Joint action of Hall and ambipolar effects in 3D magneto-convection simulations of the quiet Sun. I. Dissipation and generation of waves. Astron. Astrophys. 2020, 642, A220. [Google Scholar] [CrossRef]
- Srivastava, A.K.; Ballester, J.L.; Cally, P.S.; Carlsson, M.; Goossens, M.; Jess, D.B.; Khomenko, E.; Mathioudakis, M.; Murawski, K.; Zaqarashvili, T.V. Chromospheric Heating by Magnetohydrodynamic Waves and Instabilities. J. Geophys. Res. (Space Phys.) 2021, 126, e029097. [Google Scholar] [CrossRef]
- Solanki, S.K.; Hammer, R. The Solar Atmosphere. Century Space Sci. 2002, I, 1065–1086. [Google Scholar]
- Vernazza, J.E.; Avrett, E.H.; Loeser, R. Structure of the solar chromosphere. III. Models of the EUV brightness components of the quiet Sun. Astrophys. J. Suppl. Ser. 1981, 45, 635–725. [Google Scholar] [CrossRef]
- Karoff, C.; Metcalfe, T.S.; Santos, Â.R.G.; Montet, B.T.; Isaacson, H.; Witzke, V.; Shapiro, A.I.; Mathur, S.; Davies, G.R.; Lund, M.N. The Influence of Metallicity on Stellar Differential Rotation and Magnetic Activity. Astrophys. J. 2018, 852, 46. [Google Scholar] [CrossRef]
- Petit, P.; Dintrans, B.; Solanki, S.K.; Donati, J.-F.; Aurière, M.; Lignières, F.; Morin, J.; Paletou, F.; Ramirez, J.; Catala, C.; et al. Toroidal versus poloidal magnetic fields in Sun-like stars: A rotation threshold. Mon. Not. R. Astron. Soc. 2008, 388, 80–88. [Google Scholar] [CrossRef]
- Parker, E.N. The Generation of Magnetic Fields in Astrophysical Bodies. I. The Dynamo Equations. Astrophys. J. 1970, 162, 665–673. [Google Scholar] [CrossRef]
- Lorenzo-Oliveira, D.; Freitas, F.C.; Meléndez, J.; Bedell, M.; Ramírez, I.; Bean, J.L.; Asplund, M.; Spina, L.; Dreizler, S.; Alves-Brito, A.; et al. The Solar Twin Planet Search. The age–chromospheric activity relation. Astron. Astrophys. 2018, 619, A73. [Google Scholar] [CrossRef]
- Babcock, H.W. The Topology of the Sun’s Magnetic Field and the 22-year Cycle. Astrophys. J. 1961, 133, 572–587. [Google Scholar] [CrossRef]
- Charbonneau, P. Solar Dynamo Theory. Annu. Rev. Astron. Astrophys. 2014, 52, 251–290. [Google Scholar] [CrossRef]
- Skumanich, A. Time Scales for Ca ii Emission Decay, Rotational Braking, and Lithium Depletion. Astrophys. J. 1972, 171, 565–567. [Google Scholar] [CrossRef]
- Soderblom, D.R.; Duncan, D.K.; Johnson, D.R.H. The Chromospheric Emission–Age Relation for Stars of the Lower Main Sequence and Its Implications for the Star Formation Rate. Astrophys. J. 1991, 375, 722–739. [Google Scholar] [CrossRef]
- Rocha-Pinto, H.J.; Maciel, W.J. Metallicity effects on the chromospheric activity–age relation for late-type dwarfs. Mon. Not. R. Astron. Soc. 1998, 298, 332–346. [Google Scholar] [CrossRef]
- Lachaume, R.; Dominik, C.; Lanz, T.; Habing, H.J. Age determinations of main-sequence stars: Combining different methods. Astron. Astrophys. 1999, 348, 897–909. [Google Scholar]
- Pace, G.; Pasquini, L. The age–activity–rotation relationship in solar-type stars. Astron. Astrophys. 2004, 426, 1021–1034. [Google Scholar] [CrossRef]
- Mamajek, E.E.; Hillenbrand, L.A. Improved Age Estimation for Solar-Type Dwarfs Using Activity–Rotation Diagnostics. Astrophys. J. 2008, 687, 1264–1293. [Google Scholar] [CrossRef]
- Pace, G. Chromospheric activity as age indicator. An L-shaped chromospheric-activity versus age diagram. Astron. Astrophys. 2013, 551, L8. [Google Scholar] [CrossRef]
- Lorenzo-Oliveira, D.; Porto de Mello, G.F.; Dutra-Ferreira, L.; Ribas, I. Fine structure of the age–chromospheric activity relation in solar-type stars. I. The Ca ii infrared triplet: Absolute flux calibration. Astron. Astrophys. 2016, 595, A11. [Google Scholar] [CrossRef]
- Karoff, C.; Metcalfe, T.S.; Montet, B.T.; Jannsen, N.E.; Santos, A.R.G.; Nielsen, M.B.; Chaplin, W.J. Sounding stellar cycles with Kepler. III. Comparative analysis of chromospheric, photometric, and asteroseismic variability. Mon. Not. R. Astron. Soc. 2019, 485, 5096–5104. [Google Scholar] [CrossRef]
- Vescovi, D.; Cristallo, S.; Palmerini, S.; Abia, C.; Busso, M. Magnetic-buoyancy-induced mixing in AGB stars: Fluorine nucleosynthesis at different metallicities. Astron. Astrophys. 2021, 652, A100. [Google Scholar] [CrossRef]
- Denissenkov, P.A.; Pinsonneault, M.; MacGregor, K.B. Magneto-Thermohaline Mixing in Red Giants. Astrophys. J. 2009, 696, 1823–1833. [Google Scholar] [CrossRef]
- Salabert, D.; García, R.A.; Beck, P.G.; Egeland, R.; Pallé, P.L.; Mathur, S.; Metcalfe, T.S.; do Nascimento, J.-D.; Ceillier, T.; Andersen, M.F.; et al. Photospheric and chromospheric magnetic activity of seismic solar analogs. Observational inputs on the solar–stellar connection from Kepler and Hermes. Astron. Astrophys. 2016, 596, A31. [Google Scholar] [CrossRef]
- Mehrabi, A.; He, H.; Khosroshahi, H. Magnetic Activity Analysis for a Sample of G-type Main Sequence Kepler Targets. Astrophys. J. 2017, 834, 207. [Google Scholar] [CrossRef]
- Karak, B.B.; Kitchatinov, L.L.; Choudhuri, A.R. A Dynamo Model of Magnetic Activity in Solar-like Stars with Different Rotational Velocities. Astrophys. J. 2014, 791, 59. [Google Scholar] [CrossRef]
- Pipin, V.V.; Kosovichev, A.G. Dependence of Stellar Magnetic Activity Cycles on Rotational Period in a Nonlinear Solar-type Dynamo. Astrophys. J. 2016, 823, 133. [Google Scholar] [CrossRef]
- Karoff, C.; Knudsen, M.F.; De Cat, P.; Bonanno, A.; Fogtmann-Schulz, A.; Fu, J.; Frasca, A.; Inceoglu, F.; Olsen, J.; Zhang, Y.; et al. Observational evidence for enhanced magnetic activity of superflare stars. Nat. Commun. 2016, 7, 11058. [Google Scholar] [CrossRef]
- Balona, L.A. Flare stars across the H–R diagram. Mon. Not. R. Astron. Soc. 2015, 447, 2714–2725. [Google Scholar] [CrossRef]
- Roettenbacher, R.M.; Monnier, J.D.; Korhonen, H.; Aarnio, A.N.; Baron, F.; Che, X.; Harmon, R.O.; Kővári, Z.; Kraus, S.; Schaefer, G.H.; et al. No Sun-like dynamo on the active star ζ Andromedae from starspot asymmetry. Nature 2016, 533, 217–220. [Google Scholar] [CrossRef]
- Roettenbacher, R.M.; Monnier, J.D.; Korhonen, H.; Harmon, R.O.; Baron, F.; Hackman, T.; Henry, G.W.; Schaefer, G.H.; Strassmeier, K.; Weber, M.; et al. Contemporaneous Imaging Comparisons of the Spotted Giant σ Geminorum Using Interferometric, Spectroscopic, and Photometric Data. Astrophys. J. 2017, 849, 120. [Google Scholar] [CrossRef]
- Zhang, L.; Lu, H.; Han, X.L.; Jiang, L.; Li, Z.; Zhang, Y.; Hou, Y.; Wang, Y.; Cao, Z. Chromospheric activity of periodic variable stars (including eclipsing binaries) observed in DR2 LAMOST stellar spectral survey. New Astron. 2018, 61, 36–58. [Google Scholar] [CrossRef]
- Kaya, N.Ö.; Dal, H.A. Chromospheric activity behavior of an eclipsing binary system KOI 68AB. Astron. Nachrichten 2019, 340, 539–552. [Google Scholar] [CrossRef]
- Ramiaramanantsoa, T.; Moffat, A.F.J.; Harmon, R.; Richardson, N.D.; Howarth, I.D.; Stevens, I.R.; Piaulet, C.; St-Jean, L.; Eversberg, T.; Pigulski, A.; et al. BRITE-Constellation high-precision time-dependent photometry of the early O-type supergiant ζ Puppis unveils the photospheric drivers of its small- and large-scale wind structures. Mon. Not. R. Astron. Soc. 2018, 473, 5532–5569. [Google Scholar] [CrossRef]
- Solanki, S.K.; Krivova, N.A.; Haigh, J.D. Solar Irradiance Variability and Climate. Annu. Rev. Astron. Astrophys. 2013, 51, 311–351. [Google Scholar] [CrossRef]
- Fan, Y. Magnetic Fields in the Solar Convection Zone. Living Rev. Sol. Phys. 2009, 6, 4. [Google Scholar] [CrossRef]
- Hathway, D. The Solar Cycle. Living Rev. Sol. Phys. 2015, 7, 1–91. [Google Scholar] [CrossRef]
- Charbonneau, P. Dynamo models of the solar cycle. Living Rev. Sol. Phys. 2020, 17, 4. [Google Scholar] [CrossRef]
- Spruit, H.C. Dynamo action by differential rotation in a stably stratified stellar interior. Astron. Astrophys. 2002, 381, 923–932. [Google Scholar] [CrossRef]
- Eddy, J.A. A New Sun: The Solar Results From Skylab; Ise, R., Ed.; NASA SP-402; NASA: Washington, DC, USA, 1979.
- Weber, M.; Burrows, J.P.; Cebula, R.P. Gome Solar UV/VIS Irradiance Measurements between 1995 and 1997. First Results on Proxy Solar Activity Studies. Sol. Phys. 1998, 177, 63–77. [Google Scholar] [CrossRef]
- Gigolashvili, M.; Kapanadze, N. Behavior of Some Narrow Band of Solar Spectral Irradiance during the Solar Cycles 21. Sun Geosph. 2012, 7, 35–40. [Google Scholar]
- Andretta, V.; Busà, I.; Gomez, M.T.; Terranegra, L. The Ca ii Infrared Triplet as a stellar activity diagnostic. I. Non-LTE photospheric profiles and definition of the RIRT indicator. Astron. Astrophys. 2005, 430, 669–677. [Google Scholar] [CrossRef]
- Noyes, R.W.; Hartmann, L.W.; Baliunas, S.L.; Duncan, D.K.; Vaughan, A.H. Rotation, convection, and magnetic activity in lower main-sequence stars. Astrophys. J. 1984, 279, 763–777. [Google Scholar] [CrossRef]
- Busà, I.; Aznar Cuadrado, R.; Terranegra, L.; Andretta, V.; Gomez, M.T. The Ca ii infrared triplet as a stellar activity diagnostic. II. Test and calibration with high resolution observations. Astron. Astrophys. 2007, 466, 1089–1098. [Google Scholar] [CrossRef]
- Žerjal, M.; Zwitter, T.; Matijevič, G.; Strassmeier, K.G.; Bienaymé, O.; Bland-Hawthorn, J.; Boeche, C.; Freeman, K.C.; Grebel, E.K.; Kordopatis, G. Chromospherically Active Stars in the RAdial Velocity Experiment (RAVE) Survey. I. The Catalog. Astrophys. J. 2013, 776, 127. [Google Scholar] [CrossRef]
- Linsky, J.L.; Worden, S.P.; McClintock, W.; Robertson, R.M. Stellar model chromospheres. X. High-resolution, absolute flux profiles of the Ca ii H and K lines in stars of spectral types F0–M2. Astrophys. J. Suppl. Ser. 1979, 41, 47–74. [Google Scholar] [CrossRef]
- Wilson, O.C. Flux Measurements at the Centers of Stellar H and K Lines. Astrophys. J. 1968, 153, 221–234. [Google Scholar] [CrossRef]
- Duncan, D.K.; Vaughan, A.H.; Wilson, O.C.; Preston, G.W.; Frazer, J.; Lanning, H.; Misch, A.; Mueller, J.; Soyumer, D.; Woodard, L.; et al. Ca ii H and K Measurements Made at Mount Wilson Observatory, 1966–1983. Astrophys. J. Suppl. Ser. 1991, 76, 383–430. [Google Scholar] [CrossRef]
- Baliunas, S.L.; Donahue, R.A.; Soon, W.H.; Horne, J.H.; Frazer, J.; Woodard-Eklund, L.; Bradford, M.; Rao, L.M.; Wilson, O.C.; Zhang, Q.; et al. Chromospheric Variations in Main-Sequence Stars. II. Astrophys. J. 1995, 438, 269–287. [Google Scholar] [CrossRef]
- Wright, J.T. Radial Velocity Jitter in Stars from the California and Carnegie Planet Search at Keck Observatory. Publ. Astron. Soc. Pac. 2005, 117, 657–664. [Google Scholar] [CrossRef]
- Vaughan, A.H.; Preston, G.W.; Wilson, O.C. Flux measurements of Ca ii H and K emission. Publ. Astron. Soc. Pac. 1978, 90, 267–274. [Google Scholar] [CrossRef]
- Isaacson, H.; Fischer, D. Chromospheric Activity and Jitter Measurements for 2630 Stars on the California Planet Search. Astrophys. J. 2010, 725, 875–885. [Google Scholar] [CrossRef]
- do Nascimento, J.-D.; García, R.A.; Mathur, S.; Anthony, F.; Barnes, S.A.; Meibom, S.; da Costa, J.S.; Castro, M.; Salabert, D.; Ceillier, T. Rotation Periods and Ages of Solar Analogs and Solar Twins Revealed by the Kepler Mission. Astrophys. J. Lett. 2014, 790, L23. [Google Scholar] [CrossRef]
- Barnes, S.A.; Spada, F.; Weingrill, J. Some aspects of cool main sequence star ages derived from stellar rotation (gyrochronology). Astron. Nachrichten 2016, 337, 810–814. [Google Scholar] [CrossRef]
- Boro Saikia, S.; Marvin, C.J.; Jeffers, S.V.; Reiners, A.; Cameron, R.; Marsden, S.C.; Petit, P.; Warnecke, J.; Yadav, A.P. Chromospheric activity catalogue of 4454 cool stars. Questioning the active branch of stellar activity cycles. Astron. Astrophys. 2018, 616, A108. [Google Scholar] [CrossRef]
- Mathur, S.; García, R.A.; Morgenthaler, A.; Salabert, D.; Petit, P.; Ballot, J.; Régulo, C.; Catala, C. Constraining magnetic-activity modulations in three solar-like stars observed by CoRoT and NARVAL. Astron. Astrophys. 2013, 550, A32. [Google Scholar] [CrossRef]
- Mathur, S.; García, R.A.; Ballot, J.; Ceillier, T.; Salabert, D.; Metcalfe, T.S.; Régulo, C.; Jiménez, A.; Bloemen, S. Magnetic activity of F stars observed by Kepler. Astron. Astrophys. 2014, 562, A124. [Google Scholar] [CrossRef]
- Ferreira Lopes, C.E.; Leão, I.C.; de Freitas, D.B.; Canto Martins, B.L.; Catelan, M.; De Medeiros, J.R. Stellar cycles from photometric data: CoRoT stars. Astron. Astrophys. 2015, 583, A134. [Google Scholar] [CrossRef]
- Régulo, C.; García, R.A.; Ballot, J. Magnetic activity cycles in solar-like stars: The cross-correlation technique of p-mode frequency shifts. Astron. Astrophys. 2016, 589, A103. [Google Scholar] [CrossRef]
- Oláh, K.; Kővári, Z.; Petrovay, K.; Soon, W.; Baliunas, S.; Kolláth, Z.; Vida, K. Magnetic cycles at different ages of stars. Astron. Astrophys. 2016, 590, A133. [Google Scholar] [CrossRef]
- Fletcher, S.T.; Broomhall, A.-M.; Salabert, D.; Basu, S.; Chaplin, W.J.; Elsworth, Y.; Garcia, R.A.; New, R. A Seismic Signature of a Second Dynamo? Astrophys. J. Lett. 2010, 718, L19–L22. [Google Scholar] [CrossRef]
- Broomhall, A.-M.; Chaplin, W.J.; Elsworth, Y.; Simoniello, R. Quasi-biennial variations in helioseismic frequencies: Can the source of the variation be localized? Mon. Not. R. Astron. Soc. 2012, 420, 1405–1414. [Google Scholar] [CrossRef]
- Simoniello, R.; Finsterle, W.; Salabert, D.; Garcìa, R.A.; Turck-Chièze, S.; Jiménez, A.; Roth, M. The quasi-biennial periodicity (QBP) in velocity and intensity helioseismic observations. The seismic QBP over solar cycle 23. Astron. Astrophys. 2012, 539, A135. [Google Scholar] [CrossRef]
- Simoniello, R.; Jain, K.; Tripathy, S.C.; Turck-Chièze, S.; Baldner, C.; Finsterle, W.; Hill, F.; Roth, M. The Quasi-biennial Periodicity as a Window on the Solar Magnetic Dynamo Configuration. Astrophys. J. 2013, 765, 100. [Google Scholar] [CrossRef
- Jeffers, S.V.; Mengel, M.; Moutou, C.; Marsden, S.C.; Barnes, J.R.; Jardine, M.M.; Petit, P.; Schmitt, J.H.M.M.; See, V.; Vidotto, A.A. The relation between stellar magnetic field geometry and chromospheric activity cycles. II. The rapid 120-day magnetic cycle of τ Bootis. Mon. Not. R. Astron. Soc. 2018, 479, 5266–5271. [Google Scholar] [CrossRef]
- Schrijver, C.J. Basal heating in the atmospheres of cool stars. Astron. Astrophys. Rev. 1995, 6, 181–223. [Google Scholar] [CrossRef]
- Judge, P.G.; Carpenter, K.G. On Chromospheric Heating Mechanisms of ‘Basal Flux’ Stars. Astrophys. J. 1998, 494, 828–839. [Google Scholar] [CrossRef]
- Pérez Martínez, M.I.; Schröder, K.-P.; Cuntz, M. The basal chromospheric Mg ii h+k flux of evolved stars: Probing the energy dissipation of giant chromospheres. Mon. Not. R. Astron. Soc. 2011, 414, 418–427. [Google Scholar] [CrossRef]
- Rutten, R.G.M. Magnetic structure in cool stars. VII. Absolute surface flux in Ca ii H and K line cores. Astron. Astrophys. 1984, 130, 353–360. [Google Scholar]
- Middelkoop, F. Magnetic structure in cool stars. IV. Rotation and Ca ii H and K emission of main-sequence stars. Astron. Astrophys. 1982, 107, 31–35. [Google Scholar]
- Schrijver, C.J. Magnetic structure in cool stars. XI. Relations between radiative fluxes measuring stellar activity, and evidence for two components in stellar chromospheres. Astron. Astrophys. 1987, 172, 111–123. [Google Scholar]
- Rutten, R.G.M.; Schrijver, C.J.; Lemmens, A.F.P.; Zwaan, C. Magnetic structure in cool stars. XVII. Minimum radiative losses from the outer atmosphere. Astron. Astrophys. 1991, 252, 203–219. [Google Scholar]
- Mittag, M.; Schmitt, J.H.M.M.; Schröder, K.-P. Ca ii H+K fluxes from S-indices of large samples: A reliable and consistent conversion based on PHOENIX model atmospheres. Astron. Astrophys. 2013, 549, A117. [Google Scholar] [CrossRef]
- Pérez Martínez, M.I.; Schröder, K.-P.; Hauschildt, P. The non-active stellar chromosphere: Ca ii basal flux. Mon. Not. R. Astron. Soc. 2014, 445, 270–279. [Google Scholar] [CrossRef]
- Montez, R.; Ramstedt, S.; Kastner, J.H.; Vlemmings, W.; Sanchez, E. A Catalog of GALEX Ultraviolet Emission from Asymptotic Giant Branch Stars. Astrophys. J. 2017, 841, 33. [Google Scholar] [CrossRef]
- Uchida, Y.; Bappu, M.K.V. Chromospheric activity of late-type giants and supergiants: Reappearance of dynamo activity in the interior due to the spin-up of the core in evolution. J. Astrophys. Astron. 1982, 3, 277–296. [Google Scholar] [CrossRef]
- Schmidt, S.J.; Hawley, S.L.; West, A.A.; Bochanski, J.J.; Davenport, J.R.A.; Ge, J.; Schneider, D.P. BOSS Ultracool Dwarfs. I. Colors and Magnetic Activity of M and L Dwarfs. Astron. J. 2015, 149, 158. [Google Scholar] [CrossRef]
- Mohanty, S.; Basri, G. Rotation and Activity in Mid-M to L Field Dwarfs. Astrophys. J. 2003, 583, 451–472. [Google Scholar] [CrossRef]
- Reiners, A.; Basri, G. Chromospheric Activity, Rotation, and Rotational Braking in M and L Dwarfs. Astrophys. J. 2008, 684, 1390–1403. [Google Scholar] [CrossRef]
- Tsuboi, Y.; Maeda, Y.; Feigelson, E.D.; Garmire, G.P.; Chartas, G.; Mori, K.; Pravdo, S.H. Coronal X-ray Emission from an Intermediate-Age Brown Dwarf. Astrophys. J. Lett. 2003, 587, L51–L54. [Google Scholar] [CrossRef]
- Stelzer, B.; Micela, G.; Flaccomio, E.; Neuhäuser, R.; Jayawardhana, R. X-ray emission of brown dwarfs: Towards constraining the dependence on age, luminosity, and temperature. Astron. Astrophys. 2006, 448, 293–304. [Google Scholar] [CrossRef]
- Schmidt, S.J.; Cruz, K.L.; Bongiorno, B.J.; Liebert, J.; Reid, I.N. Activity and Kinematics of Ultracool Dwarfs, Including an Amazing Flare Observation. Astron. J. 2007, 133, 2258–2273. [Google Scholar] [CrossRef]
- Hallinan, G.; Bourke, S.; Lane, C.; Antonova, A.; Zavala, R.T.; Brisken, W.F.; Boyle, R.P.; Vrba, F.J.; Doyle, J.G.; Golden, A. Periodic Bursts of Coherent Radio Emission from an Ultracool Dwarf. Astrophys. J. Lett. 2007, 663, L25–L28. [Google Scholar] [CrossRef]
- Hallinan, G.; Antonova, A.; Doyle, J.G.; Bourke, S.; Lane, C.; Golden, A. Confirmation of the Electron Cyclotron Maser Instability as the Dominant Source of Radio Emission from Very Low Mass Stars and Brown Dwarfs. Astrophys. J. 2008, 684, 644–653. [Google Scholar] [CrossRef]
- Berger, E.; Basri, G.; Fleming, T.A.; Giampapa, M.S.; Gizis, J.E.; Liebert, J.; Martín, E.; Phan-Bao, N.; Rutledge, R.E. Simultaneous Multi-Wavelength Observations of Magnetic Activity in Ultracool Dwarfs. III. X-ray, Radio, and Hα Activity Trends in M and L dwarfs. Astrophys. J. 2010, 709, 332–341. [Google Scholar] [CrossRef]
- Rodríguez-Barrera, M.I.; Helling, C.; Wood, K. Environmental effects on the ionisation of brown dwarf atmospheres. Astron. Astrophys. 2018, 618, A107. [Google Scholar] [CrossRef]
- Sorahana, S.; Suzuki, T.K.; Yamamura, I. A signature of chromospheric activity in brown dwarfs revealed by 2.5–5.0 μm AKARI spectra. Mon. Not. R. Astron. Soc. 2014, 440, 3675–3684. [Google Scholar] [CrossRef]
- Gizis, J.E.; Monet, D.G.; Reid, I.N.; Kirkpatrick, J.D.; Liebert, J.; Williams, R.J. New Neighbors from 2MASS: Activity and Kinematics at the Bottom of the Main Sequence. Astron. J. 2000, 120, 1085–1099. [Google Scholar] [CrossRef]
- Zhang, L.; Pi, Q.; Han, X.L.; Chang, L.; Wang, D. Chromospheric activity on late-type star DM UMa using high-resolution spectroscopic observations. Mon. Not. R. Astron. Soc. 2016, 459, 854–862. [Google Scholar] [CrossRef]
- Rosario, M.J.; Heckert, P.A.; Mekkaden, M.V.; Raveendran, A.V. Spot activity in the RS CVn binary DM Ursae Majoris. Mon. Not. R. Astron. Soc. 2009, 394, 872–881. [Google Scholar] [CrossRef]
- Berdyugina, S.V. Starspots: A Key to the Stellar Dynamo. Living Rev. Sol. Phys. 2005, 2, 8. [Google Scholar] [CrossRef]
- Kron, G.E. The Probable Detecting of Surface Spots on AR Lacertae B. Publ. Astron. Soc. Pac. 1947, 59, 261–265. [Google Scholar] [CrossRef]
- Kron, G.E. A Photoelectric Study of the Dwarf M Eclipsing Variable YY Geminorum. Astrophys. J. 1952, 115, 301–319. [Google Scholar] [CrossRef]
- Chugainov, P.F. On the Variability of HD 234677. Inform. Bull. Var. Stars 1966, 122, 1–2. [Google Scholar]
- Chugainov, P.F. On the Cause of Periodic Light Variations of Some Red Dwarf Stars. Inform. Bull. Var. Stars 1971, 520, 1–3. [Google Scholar]
- Vogt, S.S. Light and color variations of the flare stars BY Draconis: A critique of starspot properties. Astrophys. J. 1975, 199, 418–426. [Google Scholar] [CrossRef]
- Schrijver, C.J.; Zwaan, C. Solar and Stellar Magnetic Activity; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Alekseev, I.Y. Observations of spotted red dwarf stars at the Crimean Astrophysical Observatory. Bull. Crime. Astrophys. Obs. 1999, 95, 69. [Google Scholar]
- Duerbeck, H.W. Constraints for Cataclysmic Binary Evolution as Derived from Space Distributions. Astrophys. Space Sci. 1984, 99, 363–385. [Google Scholar] [CrossRef]
- Eggen, O.J. Contact binaries. II. Mem. R. Astron. Soc. 1967, 70, 111–164. [Google Scholar]
- Hilditch, R.W.; King, D.J.; McFarlane, T.M. The evolutionary state of contact and near-contact binary stars. Mon. Not. R. Astron. Soc. 1988, 231, 341–352. [Google Scholar] [CrossRef]
- Maceroni, C.; Vilhu, O.; van’t Veer, F.; van Hamme, W. Surface imaging of late-type contact binaries. I. AE Phoenicis and YY Eridani. Astron. Astrophys. 1994, 288, 529–537. [Google Scholar]
- Hendry, P.D.; Mochnacki, S.W. Doppler Imaging of VW Cephei: Distribution and Evolution of Starspots on a Contact Binary. Astrophys. J. 2000, 531, 467–493. [Google Scholar] [CrossRef]
- Barnes, J.R.; Lister, T.A.; Hilditch, R.W.; Collier Cameron, A. High-resolution Doppler images of the spotted contact binary AE Phe. Mon. Not. R. Astron. Soc. 2004, 348, 1321–1331. [Google Scholar] [CrossRef]
- Rucinski, S.M.; Vilhu, O.; Whelan, J.A.J. The Lyman alpha emission in W Ursae Majoris. Astron. Astrophys. 1985, 143, 153–159. [Google Scholar]
- Li, L.; Han, Z.; Zhang, F. Structure and evolution of low-mass W Ursae Majoris type systems. II. With angular momentum loss. Mon. Not. R. Astron. Soc. 2004, 355, 1383–1398. [Google Scholar] [CrossRef]
- Hall, D.S. The Relation Between Rs-Canum and Algol. Space Sci. Rev. 1989, 50, 219–233. [Google Scholar] [CrossRef]
- Albright, G.E.; Richards, M.T. The Transient Accretion Disk in the Algol-Type Binary U Sagittae. Astrophys. J. 1995, 441, 806–820. [Google Scholar] [CrossRef]
- Richards, M.T.; Albright, G.E.; Bowles, L.M. Doppler Tomography of the Gas Stream in Short-Period Algol Binaries. Astrophys. J. Lett. 1995, 438, L103–L106. [Google Scholar] [CrossRef]
- Richards, M.T.; Jones, R.D.; Swain, M.A. Doppler Tomography and S-Wave Analysis of Circumstellar Gas in β Persei. Astrophys. J. 1996, 459, 249–258. [Google Scholar] [CrossRef]




