1. Introduction

1. Introduction

In solar-type stars, the innermost atmospheric layer, the photosphere, is located just above the surface convection zone. At larger radii, the next main solar atmospheric zone is the chromosphere (‘sphere of colour’), covering altitudes of approximately 3000–5000 km and extending through a region of partial hydrogen ionisation.

Almost all luminous stars, except for white dwarfs, feature chromospheres of some sort, although they are usually most prominent and magnetically active in lower main-sequence stars and brown dwarfs of F and later spectral types, as well as in giant and subgiant stars.

Chromospheres exhibit temperature inversion. The temperature of the solar chromosphere initially cools down from the Sun’s surface temperature (5770–5780 K) to approximately 3840 K. It then rapidly increases to temperatures in excess of 35,000 K at the onset of the solar atmospheric transition region, which extends to the corona^[1][2] [9,10]. Heating of the chromosphere to temperatures above the level required to maintain radiative equilibrium is driven by a combination of mechanical heating (pulsations and shocks), acoustic heating (pulsation-driven sound waves causing hydrodynamic shocks), magnetic fields (Alfvén waves, i.e., transverse or torsional magnetohydrodynamic waves), turbulence and ambipolar diffusion^{[3][4][5][6][7][8]} ([11,12,13,14,15,16], and references therein)—i.e., separation of oppositely charged species in a plasma owing to the effects of the ambient electric field.

In the solar chromosphere magnetic heating causes the temperature to increase to a plateau of approximately 7000 K, with the ambient density falling by orders of magnitude with respect to the region near the photosphere^[9][10] [20,21]. The 7000 K plateau results from a balance between magnetic heating and radiative cooling through collisionally excited Hα, Ca  II  K and Mg  II k radiation. The intensity of the latter lines scales with the level of non-thermal heating in the chromosphere, so that they are useful proxies for both the strength of the underlying magnetic field and the area covered by that field.

At its base, the chromosphere is homogeneous, although numerous filaments and ‘spicules’ extend up to altitudes of several ×10⁴ km. Some even reach up to some 150,000 km in the form of the solar prominences (filaments viewed side-on) associated with coronal mass ejections. Both filaments and spicules—as well as their horizontal counterparts, known as ‘fibrils’—are plumes and tendrils of luminous gas. Their presence reflects the importance of magnetic activity, e.g., organised in the form of magnetic flux tubes^[11] [22].

Chromospheric (magnetic) activity is related to photometric and spectroscopic variability on a range of timescales. Day- to year-long variability is associated with the evolution and rotational modulation of individual magnetically active regions. That is, stellar rotation is intricately correlated with chromospheric activity, as well as with stellar age. In fact, stellar rotation—particularly differential rotation—is responsible for the conversion of undisturbed poloidal magnetic fields into twisted toroidal fields (e.g., ^[12][24]).

Magnetic activity is likely triggered by the interplay of rotation and turbulent convection at the stellar surface. In turn, this triggers cyclic and self-sustained global stellar magnetic activity, including the well-known 11-year solar sunspot activity cycle ^[13][14][25,26]. Direct solar observations have been performed since approximately 1609. The wealth of observational data has allowed us to explore the significant variability of the Sun’s cycle-averaged magnetic activity level in great detail. The latter ranges from the extremely quiet ‘Maunder Minimum’ (1645–1715), when photospheric sunspots almost completely disappeared, to the present-day enhanced magnetic activity.

With increasing stellar age, the strength of the surface magnetic field—and, hence, a star’s magnetic activity—decreases in response to magnetic braking of a star’s rotation rate through angular momentum losses induced by magnetised winds and structural variations ^[15][16][32,33]. As such, quantification of a star’s chromospheric magnetic activity offers a direct stellar age measurement^{[14][17][18][19][20][21][22][23][24]} [26,34,35,36,37,38,39,40,41]. In addition, chromospheric activity relates the changes observed at the stellar surface to changes occurring deeper into the stellar interior ^[25][42], in particular for stars exhibiting solar-like dynamos (^[26][27][43,44], and references therein). Hence, its study can shed light on the physical mechanisms responsible for these changes^{[28] [29]}[45,46] and thus better constrain dynamo models^[30][31] [47,48].

Finally, magnetically active stars tend to exhibit flares or superflares (sudden releases of magnetic energy)^[32] [49], often large and rapidly evolving starspots (cooler regions where convection is suppressed by strong magnetic fields)^{[33][34][35][36][37]} [50,51,52,53,54], as well as faculae and plages (unusually bright regions in the photosphere and chromosphere, respectively)^[38][39] [8,55]. Dark starspots and bright faculae are usually located in stellar photospheres, whereas plages tend to be associated with chromospheres ^[39][55].

2. Magnetic Activity Cycles and the Solar Dynamo

2. Magnetic Activity Cycles and the Solar Dynamo

The Sun is a magnetically moderately active star exhibiting short- to long-term fluctuations. The Sun’s magnetic nature drives solar activity (i.e., solar flares, coronal mass ejections, high-speed solar winds and solar energetic particles) and, in particular, the presence and appearance of sunspots. The appearance of sunspots can be attributed to deep-seated toroidal flux ropes which rise through the Sun’s convective envelope and reach the photosphere. Whereas the stability and the rise of toroidal flux ropes are fairly well-understood^[40] [63], the process through which the diffuse, large-scale solar magnetic field produces concentrated toroidal flux ropes which will subsequently give rise to sunspots remains poorly understood.

The complex sunspot cycle can be expressed using a sunspot ‘butterfly diagram’ (see Figure 1), which shows the fractional coverage of sunspots as a function of solar latitude and time (see the reviews by ^[41][42][65,74] and references therein). In addition, assuming that the toroidal fluxes, which likely govern the appearance of sunspots, rise radially and are formed where the magnetic field is strongest, the sunspot butterfly diagram also reflects a spatio-temporal ‘map’ of the Sun’s internal, large-scale toroidal magnetic-field component.

Figure 1.Sunspot Butterfly Diagram showing the distribution of sunspots as a function of latitude, since 1874. (© Hathway ^[42]. Reproduced under a Creative Commons Attribution 4.0 International License; https://creativecommons.org/licenses/by/4.0.)

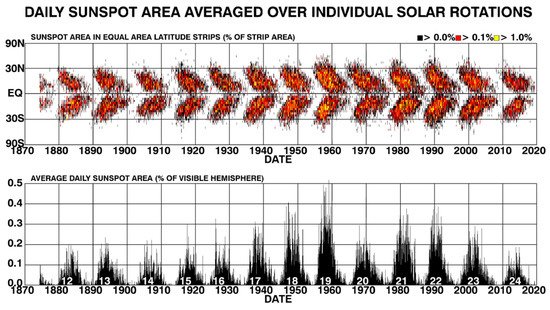
Figure 1. Sunspot Butterfly Diagram showing the distribution of sunspots as a function of latitude, since 1874. (© Hathway [65]. Reproduced under a Creative Commons Attribution 4.0 International License; https://creativecommons.org/licenses/by/4.0.)

Dynamo theory proposes that stars, including our Sun, possess physical mechanisms that generate a magnetic field. Figure 2 provides a schematic overview of the basic features of the solar dynamo. To fully understand solar (stellar) dynamo theory we have to consider the key ingredients through which a convecting, rotating and electrically conducting fluid can maintain a magnetic field over cosmic timescales. These ingredients include the turbulent motions present in convective regions or, in some cases, also in radiative zones ^[43][76]. Convection is an instability that occurs in a stratified fluid or plasma, which in turn leads to the transportation of energy through the bulk displacement of parcels of ‘fluid’. In stellar convection zones, convection carries most of the energy.

 

Figure 2. Schematic of the solar hydromagnetic dynamo. The dashed lines outline the Sun’s photosphere and the base of the convection zone, known as the ‘tachocline’. The colours show the rate of rotation within the Sun, with differential rotation occurring in the convection zone. (© Paul Higgins, 2012. doi:10.6084/m9.figshare.102094.v1. Reproduced under a Creative Commons Attribution 4.0 International License; https://creativecommonshttps://creativecommons.org/licenses/by/4.0.org/licenses/by/4.0.)

In the solar cycle context, we care about identifying the circumstances under which the flow fields observed and/or inferred in the Sun can sustain the cyclic regeneration of the magnetic field associated with the observed solar cycle.

3. Diagnostics

3. Diagnostics

One of the most frequently used indicators of chromospheric activity in cool early-F to M-type stars is the occurrence of non-thermal flux reversal in the cores of the Ca II H and K absorption lines. Ca II H and K ions originate in both the upper photosphere and the chromosphere; they are often associated with the presence of plages ^[45][108] and are sensitive to magnetic activity ^[46][109].

Although analyses of carefully selected spectral-line characteristics are preferred to obtain the highest-quality physical parameters of chromospherically active stars, integrated quantities such as bolometric flux-normalised indices ^[47][48][134,139], equivalent widths ^[49][50][132,140] and absolute chromospheric fluxes are often employed instead. 

The physical interpretation of integrated quantities is not straightforward, given that these measures are not true reflections of chromospheric radiative losses ^[51][128]. Nevertheless, the Mt Wilson chromospheric activity index,  S_MW, is the most commonly employed chromospheric activity diagnostic^{[52][53][54][55]} [144,145,146,147]. It is derived by measuring the chromospheric Ca  II  H and K line fluxes, normalised to the nearby continuum:

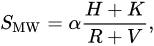
where H and K are the line fluxes measured in 1.09 Å-wide triangular bandpasses (full width at half maximum), whereas R and V represent estimates of the ‘pseudo-continuum’ on either side of the lines, measured in 20 Å-wide spectral windows; α is a normalisation constant ^[53][56][57][145,148,149].

The S_MW index requires a correction for line blanketing, i.e., the contribution from photospheric flux in the line cores. We also need to normalise the star’s bolometric luminosity. The index resulting from having applied the latter corrections is known as R_HK ^[48][56] [139,148],

where σ is the Stefan–Boltzmann constant.

Perhaps the most important diagnostic relationship allowing us to probe the physics of stars exhibiting chromospheric activity is the chromospheric activity–age relation. Until recently, it was thought that chromospheric activity declines smoothly, rapidly and monotonically with increasing age^[18][22] [35,39] for ages up to about 1.5 Gyr^[21][23] [38,40], beyond which any activity would cease.

The physical mechanism thought responsible for this behaviour is the notion that stars lose mass through coronal winds, which in turn leads to a reduction in angular momentum as well as in the torque acting on the stellar surface. In combination, these effects lead to a gradual decrease in the stellar rotation rate on million-year timescales. Thus, the extent of braking owing to the decreasing stellar rotation is directly related to a reduced efficiency in the generation and amplification of magnetic fields at the base of the convection zone^[13][24] [25,41]. Consequently, a reduction in chromospheric heating follows ^[48][139]. Observationally, this will lead to a decrease in the chromospheric flux in the cores of the diagnostic absorption lines as a function of increasing stellar age.

However, Lorenzo-Oliveira et al. ^[14][24][26,41] have challenged this paradigm. They showed, based on observations of G dwarfs in old open clusters as well as a sample of 82 solar twins, that the smooth, monotonic decrease in activity extended with high significance (characterised by a false-alarm probability of just 1%) to ages of at least  6–7 Gyr for solar-mass, solar-metallicity stars aged 0.6–9 Gyr^{[17][18][22][58][59]} [34,35,39,58,172].

4. Chromospheric Activity across the Hertzsprung–Russell Diagram

4. Chromospheric Activity across the Hertzsprung–Russell Diagram

Cool FGK-type main-sequence stars other than the Sun also routinely exhibit magnetic activity cycles^[37] [146]. However, unlike the long-term solar cycle, cool stellar magnetic activity can be categorised into three distinct types, including solar-like cyclic activity, highly variable non-cyclic activity and flat activity ^[60][70]. 

F-type stars are characterised by very thin outer convection zones. As a consequence, they exhibit irregular variability rather than proper stellar cycles ^{[61][62][63][64]}[223,224,225,226]. This may imply that the physical mechanism at the basis of this type of stellar variability differs from that driving longer-term stellar cycles ^[28][29][45,46].

G- and K-type stars, including the Sun, tend to exhibit secondary, shorter-term cycles ^{[54][65][66][67][68][69]}[146,202,227,228,229,230], which may be manifestations of a second stellar dynamo in addition to that responsible for the main stellar (and solar) cycles. It has been suggested that such secondary dynamos might be evidence of polarity-reversing solar(-like) activity cycles ^[70][231].

Chromospheric and coronal activity in evolved late-type stars remain poorly understood. Although the chromospheres in these highly evolved stars appear to be much cooler than the solar chromosphere, it has been suggested that the level of chromospheric emission remains at a basal level^[71][72][73] [161,240,241]. The ‘basal’ flux is equivalent to the low chromospheric activity boundary^{[74][75][76][77][78][79]} [154,156,157,158,159].  Chromospheric heating at these late evolutionary stages could be either due to magnetic fields or caused by pulsations or wave action (^[71][161], and references therein); the precise mechanism is as yet unresolved ^[80][236]. 

Uchida & Bappu (^[81][232] and references therein) have investigated the renewal of chromospheric activity in red giants and supergiants. These studies have revealed a likely reappearance of dynamo activity in the stellar interior which arises due to the core spin-up. This core spin-up is thought to be driven by the core contraction that occurs during the star’s evolution off the main sequence to the giant stage.

Chromospheres in fully convective M dwarfs are significantly more compressed, and hence characterised by higher densities, than in solar-type stars. Given these higher densities, Balmer-line cooling in M dwarfs is more efficient than in solar-type chromospheres, and Hα is the principal diagnostic line ^[82][246]. It is as yet unclear how M-dwarf chromospheres are heated. 

L-dwarf chromospheres are cooler and have smaller filling factors ^[82][246]. X-ray, Hα, Lyman continuum and radio emission observations of at least some brown dwarfs, particularly of types earlier than mid-L, show evidence of the presence of higher-temperature regions reminiscent of chromospheres or hot coronae in their upper atmospheres^{[83][84][82][85][86][87][88][89][90][91]} [167,168,246,248,249,250,251,252,253,254]. The implied boundary at mid-L brown dwarf types may be real and might be associated with the threshold for core hydrogen burning ^[92][255], with chromospheric activity—as traced by the ratios of the X-ray and Hα  luminosities to the bolometric luminosity—decreasing towards later types^{[83][90] [93]}[167,253,256].

5. Close Binarity and Stellar Chromospheric Activity

5. Close Binarity and Stellar Chromospheric Activity

Rapidly rotating evolved binary systems with close, tidally locked and cool components tend to be strongly magnetically active. They may, hence, exhibit chromospheric activity, e.g., in the form of Hα emission.

RS CVn systems are binary systems containing an F- to K-type giant or subgiant primary star. They feature active chromospheres—as traced by strong Ca II H and K emission—and large photospheric starspots. The latter may cover as much as 50% of the stellar surface ^[94][95][96][113,180,266]. The secondary components are G–M-type subgiants or dwarfs. They tend to be located well inside the systems’ Roche lobes. As such, these systems are close binaries which are (close to) tidally locked.

Magnetic activity similar to that seen for the Sun, in the form of strong optical flares, was first discovered on red dwarf stars of types K–M, that is, lower main-sequence stars with masses ranging from the core hydrogen-burning limit at 0.08 M_⊙ to 0.5 M_⊙ for M0-type stars^[96] [266]. Such red dwarf stars are now known after their prototype, UV Ceti. In binary systems involving red dwarf stars, periodic brightness variations of up to  ΔV∼0.5 mag (although amplitudes of 0.1 mag are more usual; ^[96][266]), were first noticed as out-of-eclipse light-curve distortions. Starspots covering up to 10% of the stellar surface as a possible cause of those distortions, combined with rotational modulation, were first proposed by Kron^{[97] [98]}[276,277] (see also^{[99][100][101]} [278,279,280]).

Composed of a red dwarf and a G- or K-type component, BY Dra objects—70% of which are close binary systems ^[102][141]—are among the most chromospherically active objects. They exhibit strong Ca  II  H and K emission out of eclipse. Spectroscopically, BY Dra systems closely resemble RS CVn systems. They can be distinguished on the basis of their luminosities, however. BY Dra systems are systematically fainter than RS CVn binaries. BY Dra light curves exhibit periods close to the systems’ rotation periods, 1–5 days ^[102][141], although the brightness variations are usually irregular between successive periods. In essence, therefore, BY Dra systems exhibit quasi-sinusoidal variability owing to rotational modulation combined with slow changes in their mean brightness caused by changes in the distribution of the spotted regions ^[103][281].

W UMa systems are low-mass, ‘overcontact’ binaries, where both solar-type components have completely filled their Roche lobes, mass transfer from the larger, more massive component to the smaller, less massive component is ongoing, and both components are tidally synchronised. As such, W UMa components share a common convective envelope. Both components of W UMa systems are characterised by rapid rotation.

They exhibit continuous light-curve variability. Approximately 0.1% of the F–K-type dwarfs in the solar neighbourhood are W UMa systems ^[104][282]; they comprise 95% of eclipsing binaries in our local volume in the Milky Way ^[105][283]. These systems are most likely formed through nuclear evolution of the most massive component in the detached phase or through angular-momentum evolution within the convective envelope^[106] [284,285].

An increasing body of evidence, including from Doppler imaging^{[107][108][109]} [286,287,288], supports the notion that W UMa systems, and in particular the primary components, exhibit strong magnetic activity in the form of starspots (covering both components; ^[96][266], and references therein), flares, strong chromospheres and coronae ^[110][289]. In turn, this suggests that these systems are subject to strong angular momentum loss and (relatively weak) magnetic braking by magnetised winds (^[111][290], and references therein). In strongly magnetised objects like W UMa systems, stellar winds are released along the coronal magnetic field lines, which have their origin in the stellar surface convection zones.

A fourth type of rapidly rotating ^[96] [266], tidally locked, semi-detached eclipsing binary systems featuring magnetic activity comprises the so-called Algol-type systems. Algols are composed of a hot, B–F-type main-sequence primary component and a cooler, less massive G–K-type subgiant secondary, which both tend to rotate synchronously with their orbital periods. The cooler component is usually characterised by a deep convective envelope that fills the star’s Roche lobe; the hotter star’s Roche lobe is not filled. Combined with their rapid rotation, these boundary conditions give rise to the occurrence of starspots and other evidence of magnetic activity ^[112][294] on the secondary component, similarly to RS CVn, BY Dra and W UMa systems.

Chromospheric activity—manifested in the form of starspots and flares—is observed through Hα and Ca II H and K emission, although not necessarily strong emission^{[113][114][115]} [295,296,297]. Since starspots only cover the cool stellar component, they can only be observed (e.g., by means of Doppler tomography) during primary total eclipses. This thus only gives us access to a single hemisphere of the cool component.