Your browser does not fully support modern features. Please upgrade for a smoother experience.

Submitted Successfully!
Thank you for your contribution! You can also upload a video entry or images related to this topic.
For video creation, please contact our Academic Video Service.
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Weihua Chen | + 1159 word(s) | 1159 | 2021-12-09 04:19:05 | | | |
| 2 | Nora Tang | Meta information modification | 1159 | 2021-12-30 01:40:52 | | |
Video Upload Options
We provide professional Academic Video Service to translate complex research into visually appealing presentations. Would you like to try it?
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Chen, W. Machine Learning Development. Encyclopedia. Available online: https://encyclopedia.pub/entry/17624 (accessed on 07 February 2026).
Chen W. Machine Learning Development. Encyclopedia. Available at: https://encyclopedia.pub/entry/17624. Accessed February 07, 2026.
Chen, Weihua. "Machine Learning Development" Encyclopedia, https://encyclopedia.pub/entry/17624 (accessed February 07, 2026).
Chen, W. (2021, December 29). Machine Learning Development. In Encyclopedia. https://encyclopedia.pub/entry/17624
Chen, Weihua. "Machine Learning Development." Encyclopedia. Web. 29 December, 2021.
Copy Citation
ML models can be classified into several types depending on the task objectives, such as regression, classification, reinforcement learning, generative models, and so on. Regarding ML models available for regression prediction, all ML models in the collected research were classified into 4 categories: traditional convex optimization-based models (TCOB models), tree models, linear regression (LR), and modern deep-learning structure models (modern DL structure).
machine learning
deep learning
1. Traditional convex optimization-based model
Two main model types are included in the TCOB model group: Support Vector Machine (SVM) and artificial neural networks (ANNs). The optimization algorithms of SVM and ANNs are based mostly on convex optimization (e.g., a stochastic gradient descent algorithm). Essentially, these two models add nonlinear data transformation based on a linear model. In addition, the methods of data transformation are different in SVM and ANNs: SVM transforms the data by means of kernel functions, while ANNs use activation functions.
The development of SVM can be divided into two stages, non-kernel SVM and kernel SVM [1][2], the latter of which is commonly applied today. The kernel function transforms input features from a low dimension to a higher dimension, simplifying the mathematical calculations in the higher-dimensional space. In practice, linear, polynomial, and Radial Basis Function (RBF) kernels are three commonly used model kernels. Kernel selection depends on the specific tasks and model performance.
Multiple Layer Perceptron (MLP), also called Back Propagation Neural Network (BPNN) [3], is the simplest neural network in this model group. MLP contains three types of layers inside: the input layer, the hidden layer, and the output layer. The input layer is a one-dimensional layer that passes independent variables organized into the network. The hidden layer receives data from the input layer and processes by a feedforward algorithm. All parameters (including the weight and bias between two adjacent layers) in the network are optimized by a backpropagation algorithm. In the training stage, the prediction result is passed to the output layer after each epoch, and network parameters are updated to better fit the predictions. In the validation or testing stage, the network parameters are frozen and make predictions directly.
After MLP was proposed, a lot of artificial neural networks (ANNs) were developed from the 1970s to the 2010s, such as the Radial Basis Function Network (RBFN) [4], ELMAN network [5], General Regression Neural Network (GRNN) [6], Nonlinear Autoregressive with Exogenous Inputs Model (NARX) [7], Extreme Learning Machine (ELM) [8], and Deep Belief Networks (DBN) [9]. One distinctive characteristic of these models is that they are relatively shallow due to the limited computing power when the models were proposed and their artificial design. For example, RBFN contains a Gaussian activation function inside the network, which is not a suitable design for a “deep” network. Furthermore, among ANNs, more layers in the network do not always mean improved prediction performance; sometimes, performance even deteriorates. Even so, ANNs are currently still effective tools for atmospheric pollution prediction due to the simplicity of model application and powerful model performance.
-
2. Tree models
The development of tree models went through two stages: basic models and ensemble models. Basic models include ID3 [10], C4.5 [11], and CART [12]. The differences between them lie in the method of selecting features and the number of branches in the tree. We will not introduce the algorithms mathematically here, as they can readily be found. As a further development of basic tree models, ensemble tree models are key to the maturity of this group of ML models. There were two ensemble ideas in the history of development: bagging and boosting. The representative bagging model is the random forest (RF) [13], which develops n sub-models from the original input data and makes a prediction by voting. The two main ideas in boosting are changing the sample weight, and fitting the residual error according to the loss function during the training stage. AdaBoost [14] uses the former idea, whereas the Gradient Boosting Decision Tree (GBDT) [15], also called the Gradient Boosting Model (GBM), uses the other idea. For now, GBDT has been improved and developed into different models, such as XGBoost [16], LightGBM [17], and CatBoost [18], which have been widely used for classification as well as regression tasks.
-
3. Linear regression
This group includes multiple regression (MLR), the Autoregressive Integrated Moving Average model (ARIMA), ridge regression [19], Least Absolute Shrinkage and Selection Operator (LASSO) [20], Elastic Net [21], and Generalized Additive Model (GAM) [22]. These models were originally designed to solve regression tasks. From the perspective of ML, ridge regression, LASSO, and Elastic Net are for the regularization of linear regression. ARIMA is a time-series function transforming unstable time series into stable series for model fitting; GAM as described here refers specifically to GAM for regression, where the target variable is the sum of a series of subfunctions. The function can be expressed as follows:
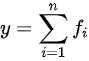
fi can be any function here.
LR has a long history of development. However, the innovation of model algorithms has stagnated since Elastic Net was proposed. One important reason for this is the limited nonlinear-fitting ability of this group.
-
4. Modern deep-learning structure models
Modern DL structure models are another important part of deep learning that evolved from the development of ANNs, which are redesigned based on MLP considering the characteristics of the prediction tasks and input data. Modern DL structure models include mainly a convolutional neural network (CNN) [23] and a recurrent neural network (RNN) [24]. CNN contains a feature-capturing filter module called a “kernel” to catch local spatial features, thus making substantial connections between neighboring layers that are sparser compared to the dense connections inside MLP. This design makes optimization and convergence of the network easier. CNN has developed many network structures with innovative model design concepts, such as AlexNet (network goes “deeper”) [25], VGG (doubles the number of layers, half the height and width) [26], ResNet (skip connection) [27], and GoogLeNet (inception block) [28]. These networks can not only be applied directly to prediction tasks, but also provide modern ideas for future network design.
Compared to CNN, RNN is better for capturing temporal relationships in a time series. This group of models retains historical data in the “memory” unit and passes them into the network in the following training. The classical RNN simply passes history information from the last time step into the network along with input data in the current time step. However, this original “memory” unit design leads to a terrible problem: a vanishing gradient, which hinders the successful training of the model. Advanced RNN-based structures such as the long short-term memory network (LSTM) [24] and gated recurrent units (GRU) [29] significantly alleviate this problem with structure modification. These advanced RNNs are now more widely applied compared to the original RNN.
During the development of modern DL structure models, several improved model components were proposed, which efficiently improved the performance of both ANNs and modern DL structure models. For instance, a sigmoid activation function was replaced by the Rectified Linear Unit (ReLU) [30] or LeakyReLU [31] in most regression tasks; the dropout method [32] was usually applied in the model training stage to alleviate overfitting; Adam [33] and weight decay regularization [34] are commonly used in network optimization.
References
- Cortes, C.; Vapnik, V. Support vector machine. Mach. Learn. 1995, 20, 273–297.
- Soman, K.; Loganathan, R.; Ajay, V. Machine Learning with SVM and Other Kernel Methods; PHI Learning Pvt. Ltd.: New Delhi, India, 2009.
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386–408.
- Broomhead, D.S.; Lowe, D. Radial Basis Functions, Multi-Variable Functional Interpolation and Adaptive Networks; Royal Signals and Radar Establishment: Worcestershire, UK, 1988.
- Elman, J.L. Finding structure in time. Cogn. Sci. 1990, 14, 179–211.
- Specht, D.F. A general regression neural network. IEEE Trans. Neural Netw. 1991, 2, 568–576.
- Lin, T.; Horne, B.G.; Tino, P.; Giles, C.L. Learning long-term dependencies in NARX recurrent neural networks. IEEE Trans. Neural Netw. 1996, 7, 1329–1338.
- Huang, G.-B.; Zhu, Q.-Y.; Siew, C.-K. Extreme learning machine: A new learning scheme of feedforward neural networks. In Proceedings of the 2004 IEEE International Joint Conference on Neural Networks (IEEE Cat. No. 04CH37541), Budapest, Hungary, 25–29 July 2004; pp. 985–990.
- Hinton, G.E.; Osindero, S.; Teh, Y.-W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554.
- Quinlan, J.R. Induction of decision trees. Mach. Learn. 1986, 1, 81–106.
- Quinlan, J.R. Improved use of continuous attributes in C4. 5. J. Artif. Intell. Res. 1996, 4, 77–90.
- Grajski, K.A.; Breiman, L.; Di Prisco, G.V.; Freeman, W.J. Classification of EEG spatial patterns with a tree-structured methodology: CART. IEEE Trans. Biomed. Eng. 1986, 1076–1086.
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32.
- Freund, Y.; Schapire, R.E. Experiments with a new boosting algorithm. In Proceedings of the ICML, Long Beach, CA, USA, 9–15 June 2019; pp. 148–156.
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232.
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd acm Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794.
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. Lightgbm: A highly efficient gradient boosting decision tree. Adv. Neural Inf. Process. Syst. 2017, 30, 3146–3154.
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased boosting with categorical features. arXiv 2017, arXiv:1706.09516.
- Hoerl, A.E.; Kennard, R.W. Ridge regression: Biased estimation for nonorthogonal problems. Technometrics 1970, 12, 55–67.
- Tibshirani, R. Regression shrinkage and selection via the lasso: A retrospective. J. R. Stat. Soc. Ser. B 2011, 73, 273–282.
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B 2005, 67, 301–320.
- Hastie, T.; Tibshirani, R. Generalized additive models: Some applications. J. Am. Stat. Assoc. 1987, 82, 371–386.
- LeCun, Y.; Boser, B.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D. Backpropagation applied to handwritten zip code recognition. Neural Comput. 1989, 1, 541–551.
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780.
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1097–1105.
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556.
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778.
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9.
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078.
- Glorot, X.; Bordes, A.; Bengio, Y. Deep sparse rectifier neural networks. In Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics, Ft. Lauderdale, FL, USA, 11–13 April 2011; pp. 315–323.
- Xu, B.; Wang, N.; Chen, T.; Li, M. Empirical evaluation of rectified activations in convolutional network. arXiv 2015, arXiv:1505.00853.
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958.
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980.
- Krogh, A.; Hertz, J.A. A simple weight decay can improve generalization. In Proceedings of the Advances in Neural Information Processing Systems, Denver, CO, USA, 30 November–3 December 1992; pp. 950–957.
More
Information
Subjects:
Meteorology & Atmospheric Sciences
Contributor
MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register
:
View Times:
908
Entry Collection:
Environmental Sciences
Revisions:
2 times
(View History)
Update Date:
30 Dec 2021
Notice
You are not a member of the advisory board for this topic. If you want to update advisory board member profile, please contact office@encyclopedia.pub.
OK
Confirm
Only members of the Encyclopedia advisory board for this topic are allowed to note entries. Would you like to become an advisory board member of the Encyclopedia?
Yes
No
${ textCharacter }/${ maxCharacter }
Submit
Cancel
Back
Comments
${ item }
|
More
No more~
There is no comment~
${ textCharacter }/${ maxCharacter }
Submit
Cancel
${ selectedItem.replyTextCharacter }/${ selectedItem.replyMaxCharacter }
Submit
Cancel
Confirm
Are you sure to Delete?
Yes
No




