Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Francisco Cruz-Sosa
 + 4383 word(s) 4383 2021-12-23 09:40:39 |
2 format correct
Conner Chen
 Meta information modification 4383 2021-12-29 01:38:06 |

Video Upload Options

Do you have a full video?
Send video materials Upload full video

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Cruz-Sosa, F. Plant Cell Culture. Encyclopedia. Available online: https://encyclopedia.pub/entry/17561 (accessed on 17 May 2024).
Cruz-Sosa F. Plant Cell Culture. Encyclopedia. Available at: https://encyclopedia.pub/entry/17561. Accessed May 17, 2024.
Cruz-Sosa, Francisco. "Plant Cell Culture" Encyclopedia, https://encyclopedia.pub/entry/17561 (accessed May 17, 2024).
Cruz-Sosa, F. (2021, December 26). Plant Cell Culture. In Encyclopedia. https://encyclopedia.pub/entry/17561
Cruz-Sosa, Francisco. "Plant Cell Culture." Encyclopedia. Web. 26 December, 2021.
Plant Cell Culture
Edit
This entry is adapted from the peer-reviewed paper 10.3390/plants10122762

The large-scale production of plant-derived secondary metabolites (PDSM) in bioreactors to meet the increasing demand for bioactive compounds for the treatment and prevention of degenerative diseases is nowadays considered an engineering challenge. Plant cell culture (PCC) is nowadays recognized as a promising, renewable, sustainable, and environmentally friendly alternative to obtain PDSM out of wild plants. PCC accounts for the virtues of whole-plant cultivation systems and offers significant advantages, such as controlled manufacture due to standardized environmental conditions, i.e., it is not seasonal dependent, makes use of low amounts of water, and pesticides and herbicides are not required, achieving better quality in the desired product.

medicinal plant bioactive compounds plant-derived secondary metabolites (PDSM) cell suspension culture (CSC)

1. Types of Cell Cultures

Calluses relate to the massive growth of cells and the buildup of agglomerated dedifferentiated cells, that may be able to revamp the complete plant, acquiring features like meristematic cells and developing new stem cells, which are able to form new individual plants [1]. Somatic embryos are obtained by the tissue formation from somatic cells or callus, having as the main objective the micropropagation of species seeds. Hairy roots culture is usually obtained by the infection of plant cells with Agrobacterium rhizogenes, resulting in the transformation of callus into differentiated tissues [2].
Even though there are several studies where the production of PDSM from callus cultures and differentiated cells/tissues are used, the cell suspension culture from dedifferentiated cells is mostly preferred [3][4]. Cell suspension cell culture (CSC) is considered as a simple and cost-effective method, allowing suitable conditions for cells to produce compounds identical to those from parental cells to be achieved, offering advantages such as setting stable systems for continuous PDSM production with homogeneity in yields and quality, as well as offering the possibility of synthesizing new compounds and greater potential for PDSM commercial application [3][5]. Therefore, CSC has been demonstrated to be the selected biotechnological tool for obtaining high-value PDSM, such as taxol [5][6], resveratrol [7][8], and ginsenosides [9], among others. To this end, further discussions will be centered on CSC for producing PDSM at laboratory and larger scales using different bioreactor configurations. Table 1 shows recent successful examples where plant cell culture is used for producing PDSM with pharmacological relevance.
Table 1. PDSM from medicinal plants successfully produced in the in vitro plant cell culture, bioactivities, and yield comparison.
Compound Plant Species Biological Activity/
Pharmaceutical Use		 Extraction Yield Type of Culture Ref.
Mother Plant In Vitro Cell Culture
Shikonin Lithospermum erythrorhizon
Alkanna tinctoria Tausch		 Anticancer, antibacterial, anti-inflammatory, hepatic steatosis attenuator, antitumor, and antioxidants 10−20 mg/g 150−200 mg/g CSC [10][11][12][13][14]
Echium plantagineum L. 36.25 mg/L HRC [15]
Anthraquinones Morinda citrifolia
Rubia cordifolia
Senna obtusifolia		 Antimicrobial, antifungal, hypotensive, analgesic, antimalarial, gastroprotective, antioxidant, hepatoprotective and antileukemic, and mutagenic functions 3 mg/g 100–200 mg/g HRC
CCC
CSC		 [16][17][18][19]
Rosmarinic acid Ocimum basilicum Antioxidant, anti-inflammatory, antiviral activities 8.78–9.4 mg/g 12.32–21.28 mg/g CSC [20][21]
Origanum vulgare 23.53 mg/g 31.25 mg/g CSC [22][23]
Satureja khuzistanica 12 mg/g 38 mg/g CSC [24][25]
Coleus blumei 30 mg/g 270 mg/g CSC [26]
Salvia officinalis 30 mg/g 360 mg/g CSC
Berberine Thalictrum minus Effects antitumor, anticancer, lower blood lipid, lower blood glucose, anti-osteoporosis, anti-osteoarthritis, antibiotic, and anti-inflammatory 0.1 mg/g 0.8 mg/mL CSC [27][28][29][30][31][32]
Coptis japonica 20–40 mg/g 132 mg/g CSC
Coscinium fenestratum 1 mg/g 178 mg/g CCC
Ginsenosides Panax ginseng Antitumor, immunological, anti-inflammation, anticancer, antidiabetic, and cardiovascular-protective 0.015–8 mg/g 36.4–80 mg/g HRC [9][33][34]
3.4–28.9 mg/g CSC
15.1–105.6 mg/g ARC
Panax japonicus 20–50 mg/g CSC
Panax notoginseng 60 mg/g CCC
71.94 mg/g ARC
40 mg/g CSC
Diosgenin Dioscorea deltoidea Anticancer, antidiabetic, anticoagulant, antithrombosis, anti-inflammatory, antiviral, anti-ageing 0.4−3 mg/g 72 mg/g CSC [35]
3.5–16 mg/g CCC
Dioscorea bulbifera 12 mg/g CCC
Helicteres isora L. 1–5 mg/g 8.64 mg/L CSC [36]
23 mg/g CCC [37]
Ajmalicine Catharanthus roseus Antihypertensive, obstructive circulatory diseases treatment 3 mg/g 63 mg/L CCC [38]
10 mg/g CSC [39][40]
34 mg/L HRC
Paclitaxel Taxus chinensis Anticancer 0.02 mg/g 1.5 mg/g CSC [41]
Podophyllotoxin Linum narbonense Vigorous antimitotic and antiviral activities and anticancer 0.5 mg/g 1.57 mg/g CCC [42]
Juniperus chinensi 0.025 mg/g 189.91 mg/g CSC
Linum flavum 1.6 mg/g 2 mg/g CSC
Artemisinin Artemisia annua L. Treat multi-drug-resistant strains of falciparum malaria 1–15 mg/g 9.33–110.2 mg/L CSC [43][44]
Phenolic Acids Verbena officinalis Antimicrobial, secretolytic, expectorant, and diuretic agent 136.59 mg/g 126.55 mg/g CCC [45]
(rosmarinic, chlorogenic, and ferulic acid) 189.91 mg/g CSC
Resveratrol Vitis vinifera L. Reduced coronary heart disease mortality rates and atherosclerosis, inhibiting low-density lipoprotein oxidation, and carcinogenesis NR 277.89 µg/g CSC [46]
CSC means cell suspension culture; HRC means hairy root culture; CCC means callus cell culture, ARC adventitious root culture; NR means not reported.

2. Plant Cell Suspension Culture

Plant cell suspension culture (CSC) represents a cost-effective and simple biological process for the synthesis of PDSM at large scales [3]. This production concept takes advantage of plant cells as biosynthetically totipotent structures, being capable of obtaining bioactive compounds with identical properties to those contained in plant stem cells, offering potential advantages regarding quality and yield of PDSM [3][47]. To this end, although there are engineering challenges, CSC offers greater potential for industrial applications in large-scale bioreactors than plant tissue and organ cultures. Although the latter ones offer better genetic stability in propagated cells, the design of the bioreactors for their maintenance usually requires greater investments and careful experimentation in the preliminary scale-up stage [48][49].
At a laboratory scale, CSC, in general, uses dedifferentiated plant cells and involves four essential stages as shown in Figure 1 [48].
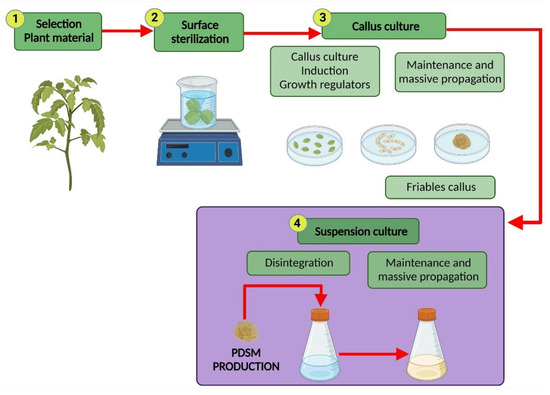
Plants 10 02762 g002 550
Figure 1. General steps for obtaining cell suspension culture. PDSM means plant-derived secondary metabolites. * Schemes were created with BioRender.com.
Success in the operation of suspension cultures depends on the induction and obtention of friable callus (stage 3) through the exposure to growth regulators, such as auxins and cytokinin. The final step (stage 4) comprises the transfer and maintenance of this cell culture in a liquid. CSC may become unstable when subjected to prolonged culture times, causing differences in the quality and quantity of PDSM; this behavior is due to the consumption and reduced availability of nutrients in the culture media, in addition to genetic variations that can restrict the conservation of the high-yield cell line [50]. Among the strategies used for improving the production of PDSM in CSC is the modification in the culture media composition (different carbon, nitrogen, and phosphorous sources) for optimizing the nutrient availability during the culture time [51][50], and the use of biotic or abiotic elicitors that trigger the defense response from plant cells promoting the secondary metabolism through the introduction of chemical or physical stresses [46][3][52]. Biotic elicitors are complex compounds derived from biological sources, including plant-derived polysaccharides, such as pectin and cellulose, and microbial-derived polysaccharides, such as chitin and glucan [51][53], and plant immune-signaling molecules, such as jasmonic acid [54], salicylic acid [55][56], and methyl jasmonate [54]. Abiotic elicitors include inorganic salts, heavy metals, UV irradiation, high salinity, and pressure [57].

3. Commercial Production of PDSM from CSC

The current production of various drugs, cosmetics, and food ingredients is obtained using plant cell cultures, especially in the form of CSC, as these offer several advantages over other technologies, such as better control during the production of PDSM, a larger feasibility for the scaling up of the process, and shorter production cycles, being environmentally responsible and sustainable processes. The application of CSC to obtain commercial products dates back to the 1960s [46][50][58][59]. Table 2 shows a selection of plant cell extracts that have been successfully manufactured at a commercial scale for pharmaceutical purposes. So, by way of history, the first report about industrial manufacturing of bioactive compounds derived from CSC was found for Shikonin from L. erythrorhizon by Mitsui Petrochemical Ind., now Mitsui Chemicals, Inc. (Tokyo, Japan). To date, Taxol®, manufactured by Phyton Biotech, Inc. (Delta, BC, Canada), and Genexol, the commercial name for paclitaxel compound by Samyang Genex, represent the cancer drugs with greater demand in the market, with annual sales reaching up to 200–300 kg per year [60]. In agreement with the information available at the website for manufacturers, the production volume for PDSM increases from a few cubic meters to 75 m3 equivalent, to reach 880 m3 per year [61].
Table 2. Plant-derived products manufactured from plant CSC which have entered into the pharmaceutical industry. The list of products makes no claim to be complete.
Product Species Pharmaceutical Use Manufacturer, Tradename, and
Scale of Production		 Type of Culture Reference
Rosmarinic acid Coleus blumei Anti-inflammatory ANattermann & Cie. Gmbh,
www.sanofi.de (accessed on 30 October 2021)		 CSC [62]
Echinacea polysaccharides Echinacea purpurea Immunostimulant, anti-inflammatory Diversa, 75,000 L bioreactor CSC [59][63]
Berberines Thalictrum minun Anticancer; antibiotic; anti-inflammatory Mitsui Chemicals, Inc., (75,000 Lbr) CSC [64]
Coptis japonica https://www.mitsuichemicals.com/ (accessed on 30 October 2021) CSC
Podophyllotoxin Podophyllum spp. Anticancer Nippon Oil Company, Ltd. CSC [65]
https://www.freepatentsonline.com/5336605.html (accessed on 30 October 2021) OC [66]
Docetaxel Taxus baccata Ovarian cancer treatment Phyton Biotech, Inc., Taxotere (150 kg/year) CSC [67][68]
https://phytonbiotech.com/ (accessed on 30 October 2021)
Paclitaxel Taxus spp. Anticancer: FDA approved for the treatment of ovarian, breast, and lung cancers Phyton Biotech, Inc., Taxol ® (1000 kg/year) CSC [69]
https://phytonbiotech.com/ (accessed on 30 October 2021)
Samyang Genex Corporation., Genexol (32,000 Lbr) https://samyangbiopharm.com/eng/ProductIntroduce/injection01 (accessed on 30 October 2021) CSC [70]
[71]
Scopolamine Duboisia spp. Anticholinergic; antimuscarinic; motion sickness, nausea, and intestinal cramping Sumitomo Chemical Co., Ltd., Tokyo, Japan
(50–20,000 Lbr) https://www.sumitomo-chem.co.jp/pharma-chem/ (accessed on 30 October 2021)		 HRC [72][73]
Shikonin Lithospermum erythrorhizon Anti-HIV, antitumor, anti-inflammatory Xi’an NEO Biotech, Shikonin 95% CSC [59]
http://www.extractneo.com/about (accessed on 30 October 2021)
CSC: cell suspension culture; HRC: hairy root culture; OC: organ culture.

4. Typical Bioreactor Configurations

Bioreactors are defined as containers used to provide a controlled environment to transfer nutrients and oxygen to cell cultures in adequate concentrations that allow the cell to maintain its primary and secondary metabolic activity. Because plant cells, as well as other micro-organisms, are more sensitive and less stable than chemical compounds, bioreactor designs must be robust enough to provide a greater degree of control over process disturbances and contamination and achieve high productivities, high quality products, and cost effectiveness. The bioreactor design and its optimal operation depend on the determination of the operating conditions giving rise to the required product formation, minimizing the cost of the process [74]. The most common bioreactor configurations utilized for commercial and large-scale production consist in stirred tank bioreactor (STB), wave stirred bioreactor (WSB), air-lift bioreactor (ALB), and bubble column (BC). The selection of the bioreactor configuration is frequently established by its optimal performance in terms of metabolic activity and kinetics of cell cultures, economic costs, and its flexible operation regarding maintenance of cultures by controlling operational conditions, such as temperature, pH, aseptic, mixing, aeration, and scalability. Table 3 shows some characteristics, advantages, and disadvantages of these types of bioreactors.
Table 3. Comparison of bioreactor configurations commonly used for plant cell culture.
Bioreactor Configuration Schematic Diagram * Description Advantages Disadvantages Ref.
Bubble
column (BC)		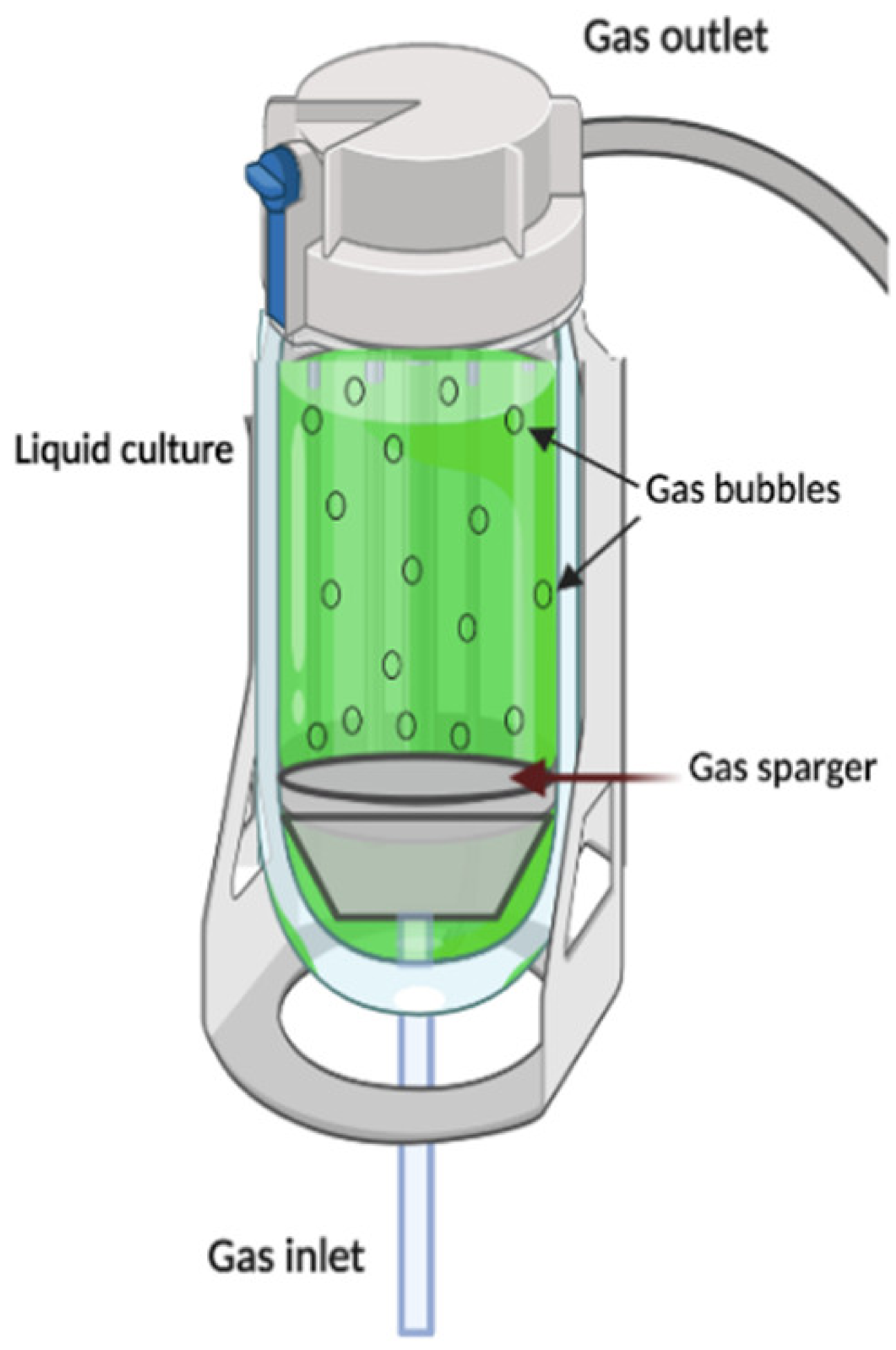 Plants 10 02762 i001 It is classified in the pneumatic-type bioreactor. They are constructed in cylindric columns where gas injection represents the only energy entrance to the system. BC bioreactors operate under constant bubbling where gas flows from the bottom to the top through nozzles, perforated plates, or spray rings, allowing not only the aeration process, but also helping the mixing and circulation of the fluid, without the need to install mechanical accessories. Simple structure as no mechanical force is required to shake.
Easier maintenance and reduces the risk of contamination due to the lack of mobile parts.
Reduced effect of the shear stress.		 High foam formation under high gas flow rates.
Poor oxygen transfer capabilities.
Poor fluid mixing in highly viscous fluids.
High levels of foaming under high-aeration conditions		 [58][49][75]
Airlift (ALB) 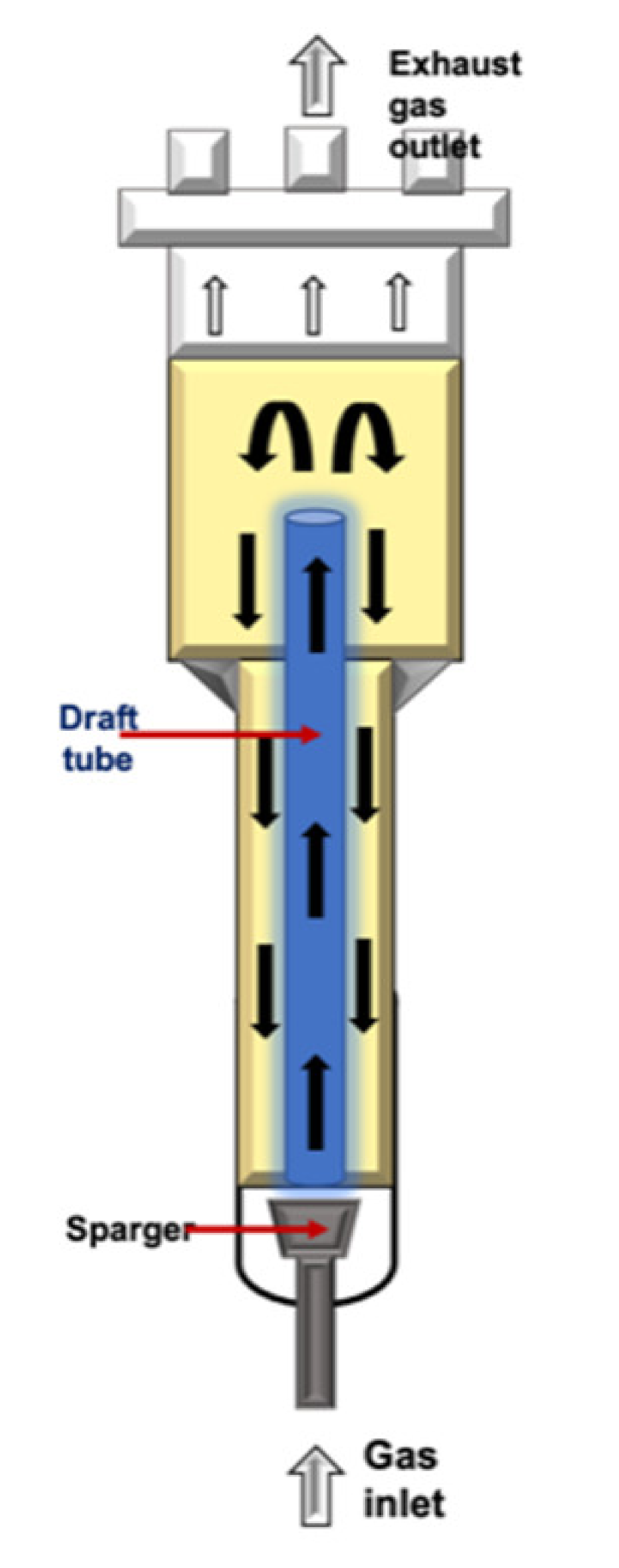Plants 10 02762 i002 It is classified in the pneumatic-type bioreactor. This configuration is considered reasonably like STR, excepting for the impeller. They are tower reactors where fluid broth is mixed with a gas stream, which is compressed and injected at the bottom of the discharge pipe. The gas–fluid mix allows the creation ofdifferences in density and upward displacement. It is more suitable for hairy root and somatic embryo cultures. Easy maintenance and reduces the risk of contamination due to the absence of mobile parts.
Reduced effect of the shear stress.
Higher oxygen transfer than that in BC.
The energy required is provided by the compressed gas.		 High levels of foam formation under high gas flow rates.
Poor fluid mixing in highly viscous fluids.
Relatively poor oxygen transfer capabilities.		 [58][76][77][78]
Stirred tank bioreactor (STB) Plants 10 02762 i003 It is grouped in the mechanically agitated bioreactor. This bioreactor consists in a mixer (turbine or propeller) installed within the tank reactor and may be equipped with gassing inlet stream. It can operate in batch, semi-continuous, or continuous mode [76][79]. Efficient fluid mixing systems.
High oxygen mass transfer capability.
Convenient for high-viscous fluids.
Comply with Good Manufacturing Practices.
Easy scale-up.
Highly adaptable to production scale and products.
Impeller alternative.		 High energy cost owing to mechanical agitation.
Contamination risk with mechanical seal.
Some cells and metabolites are susceptible to shearing generated by the impeller and bursting gas bubbles. Depending on the operation mode, this configuration can represent high costs of maintenance, cleaning, and startup.		 [49][76][79][80]
* Schemes were created with BioRender.com.

Engineering Aspects in the Plant Cell Suspension Culture

Engineers designing or optimizing bioreactor technologies must both consider the effect of operating conditions on the complex interaction between transport phenomena, thermodynamics, growth kinetics, metabolic activity, and maintenance of plant cell cultures and, based on it, propose methodologies to transfer information observed in flask cultures to larger bioreactor scales. Some operational conditions are critical because they can cause a decrease in biomass, a low PDSM production, or a loss of cell viability. Table 4 shows some CSC that have been successfully scaled from flask cultures to large-scale bioreactors.
Table 4. Comparison of operating conditions used for SCC in flask and bioreactor to produce PDSM. The list of examples makes no claim to be complete.
Species Compounds Operation Variables Evaluated Biomass
Production		 PDSM
Production		 Ref.
In Shake Flask In
Bioreactor		 In Shake Flask In Bioreactor
Scrophularia striata Phenylethanoid glycosides 50 mL SCC in 100 mL flask
110 rpm
25 °C		 5.0 L SCC in STR 10 L
Fg: 0.5–1.0 L/min
110−170 rpm
25 ± 1 °C
Darkness		 14.16 g/L 15.64 g/L The acteoside content in CSC in the bioreactor was about threefold higher than that in the shake flask [81]
Buddleja cordata Verbascoside,
linarin and hydroxycinnamic acids		 50 mL SCC in 250 mL flasks
110 rpm
26 ± 2 °C		 STR 2 L
Fg: 1 vvm (ring diffuser
Rushton impeller 400 rpm
26 ± 2 °C
16/8 h light to dark photoperiod		 11.8 g/L 13.62 g/L The content of phenolics was twofold higher in STR. [82][83]
Rubia
tinctorum		 Anthraquinone 25 mL SCC in 250 mL flasks
100 rpm
25 ± 2 °C
16/8 h photoperiod
(140 µmol m−2 s−1)		 1.0 L SCC in STR 2 L
Fg: 1 vvm
Turbine impeller 450 rpm
25 ± 2 °C
16/8 h photoperiod
(140 µmol m−2 s−1)		 330 g/L 220 g/L Anthroquinone production was 2.5 times higher in STR [84]
Arnebia sp. Shikonin 25 mL CSC in 250 mL flasks Air-lift bioreactor 1249.2 g/L 480 g/L The shikonin content was 2.6 times higher in the bioreactor than in the flask. Production remained without significant differences in both bioreactors [85]
100 rpm 2 L working volume
25 ± 2 °C 25 ± 2 °C
Continuous light Fg: 2 L/min (sparger ring)
(70 µmol/m2 s 1)  
  STR 2 L 1249.2 g/L 450 g/L
  Six-blade turbine impeller 100 rpm
  Fg: 2 L/min
  25 ± 2 °C
Ocinum basilicum Rosmarinic acid 100 rpm 7 L CSC in STR 10 L Biomass was 8.4 times higher in bioreactor than in flask Production increased 1.66 times in bioreactor [21]
25 ± 2 °C Marine impeller 100 rpm
  Fg: 25 L/min
Satureja khuzistanica Rosmarinic acid 200 mL CSC in 1 L flask 1 L CSC in culture bags 2 L 13.6 g/L 18.7 g/L Production increased 2.5 times in bioreactor [86]
110 rpm Batch mode
25 °C 20–30 rpm
  25 °C
  Fg: 0.1 vvm
  Darkness
Vitis labrusca L. Resveratrol 100 mL CSC in 300 mL flasks STR 5 L NR ≈35 g DW Production increased 1.15 times in bioreactor [87]
110 rpm Marine impeller 110 rpm
23 °C Fg: 0.15 vvm
Darkness  
Santalum album L. Squalene 100 mL CSC in 250 L flask Airlift bioreactor 7 L 1.05 mg/g 1.25 mg/g Production increased 1.71 times in bioreactor in four weeks of culture [88]
90 rpm Batch mode
28 °C 70–80 rpm
  Fg: 4 L/min
  28 ± 2 ° C
NR means Not reported.
The scaling up of CSC carried out in a flask culture demands the use of bioreactor engineering to characterize the impact of operating conditions on growth kinetics, cell deactivation, and transport phenomena and, hence, on the metabolic activity and production rates of PDSM. To this end, in what follows, main aspects to be considered during the scaling up of CSC, from the screening of plant cells to the industrial-scale bioreactor design, are mentioned and analyzed.
The screening of a set of plant cells is considered as the first stage during the scaling up of CSC [48][49]. Screening takes place in shake flasks. In these laboratory bioreactors, hydrodynamic and transport phenomena negatively impact on the growth kinetics, cell viability, metabolic activity, and production rates of PDSM. For instance, in these bioreactors, the production of PDSM involves two-phase systems (liquid culture phase and cell culture phase) neglecting the effect of operating conditions, including the impact of the oxygen concentration, on the microscopic and macroscopic performance of the shake flask. In this context, apparent results regarding cell growth kinetics, cell viability rates, and production rates of PDSM are observed. In these conditions, promising plant cells are identified and selected to be evaluated in larger bioreactor configurations, such as those presented in Table 3.
The second step accounts for characterization of cell growth kinetics, cell viability rates, metabolic activity, and production rates of PDSM under controlled operating conditions in bench-scale bioreactors with similar configurations to those systems to be implemented at the commercial scale, i.e., bench-scale bioreactors accounting for three phases (liquid–gas–cells) (see Table 3). Thus, during the analysis of bench-scale systems, the coupling of experimentation with mathematical modeling is essential for stating the basis for the scaling up of CSC [89][90][91]. Herein, cell growth kinetics and production rates of PDSM are the main response variables to maximize during CSC. It is worth mentioning that their experimental and theoretical characterization makes possible the connection between the microscopic world of the metabolic cell activity and the macroscopic world of the bioreactor performance and, hence, the downstream processing. Besides, the experimental characterization of these cell mechanisms and their analysis using mathematical models lead to the construction of the engineering tool for the scaling up and optimization of the bioreactor configuration, allowing a better understanding of CSC during the production of PDSM. In particular, the use of bench-scale bioreactors allows for identifying and controlling those operating conditions where transport phenomena favor the kinetics of the CSC.
Based on the kinetics, since in CSC it is not possible to develop intrinsic kinetic models, there are two types of models that can be developed in bench-scale bioreactors: extrinsic ones, where transport phenomena are explicitly included during the modeling of the bioreactor; and apparent ones, where transport phenomena resistances impact during the experimentation but they are not considered during the modeling of the bench-scale bioreactors [90][92][93][94][95][96]. Thus, to determine extrinsic kinetic models, it is recommended to carry out a regime analysis to identify and model those transport phenomena limiting the production of PDSM. Experiments make possible the development of the corresponding model, relating kinetics with macroscopic variables, namely the concentration of substrates and PDSM, cell growth, and cell viability involved during the operation of the bench-scale bioreactor. The kinetic model depends on the quality of the experimental data and it is only reliable for the range of operational conditions utilized during its development. When the kinetic model is based on metabolic steps of the reaction, the mathematical complexity increases but leads to a better physical representation of the CSC during the production of PDSM. Besides, the loss of cell viability caused by operational aspects, i.e., a toxic compound, cell shear stress, or cell sintering, is modeled by empirical expressions whose parameters involve physical meaning [97], such as the generalized power law equation (GPLE) [98][99][100]. Finally, the Monod model offers an adequate explanation for the reaction rates of growing cells, but it has no mechanistic basis [101][102]. Moreover, the Monod model is only applicable when cells are in a metabolic equilibrium, namely when the composition of the macromolecules in the cell remains in a pseudo-steady state during the CSC. Table 5 presents some kinetic models to describe cell growth rate. It is worth mentioning that, in transient experiments, when the concentration of a substrate or PDSM is brusquely modified, Monod kinetics are not suitable and the kinetic model must account for the cell metabolism [97][103]. There are, in the literature, several models that have no mechanistic grounds but account for some biological features of the cell growth [97][104]. These models offer an acceptable description of the cell growth and metabolic activity due to fluctuation in the concentration of substrates and products. In these models, cell mass is divided into compartments, and the rate of formation of each compartment has different stoichiometry and kinetics.
Table 5. Models used to describe kinetics and deactivation in whole cells [96][99][100][101].
Mathematical Equation Conventional Name
rx=µ=µmax[Si][Si]+Kmrs=Yxsµ Monod kinetics
rx=µ=µmax[Si]([Si]2/Ki)+[Si]+Kmrs=Yxsµ Expanded Monod kinetics
rx=µ=µmax[Si][Si]+Km(1−[P][P]max)rs=Yxsµ Expanded Monod kinetics
rx=µ=µmax(1−exp(−[Si]/Km))rs=Yxsµ Monod’s teacher Tessier kinetics.
rx=µ=µmax[Si][Si]+KSXrs=Yxsµ Contois kinetics.
rx=µ=µmax(1−XKS)rs=Yxsµ Logistic kinetics.
dθxdt=−kin(θx−θss)mr=rs=θxk[Si][Si]+Km Cell deactivation kinetics
In bench-scale bioreactors, it is experimentally complicated to minimize transport resistances [98][99][100][105]. In the fluid bulk, concentration, temperature, or radiative gradients can be present. Hydrodynamics impact on mass and heat transfer mechanisms from the gas phase to the liquid phase and from the liquid phase to the cell phase. Moreover, cell growth can impact on mass and heat transfer mechanisms. Although complicated, a proper kinetic analysis must account for the effect of fluid dynamics on transport phenomena and, hence, on cell growth, cell viability, and metabolic activity.
During the screening at the laboratory bioreactors or during the operation of the bench-scale bioreactor, the response surface methodology (RSM) is a potential tool to guide experimental designs. RSM leads to the following advantages [106][107][108][109][110]:
(1)
It defines an establishment of the relationship between responses (yield, cell viability, oxygen concentration, etc.) and control operating conditions (temperature, pressure, initial concentration, power input, agitation rate, etc.).
(2)
It predicts the effect of control operating condition on responses.
(3)
It gives inferences on the significance of the operating conditions on the performance of the reactor.
(4)
It allows the determination of the operating window where the bioreactor meets its best performance.
On the above end, RSM couples experimental designs, and mathematical and statistical methods [111][112]. Firstly, an experimental design is proposed; the evaluation of this experimental design constitutes the so-called response surface design (RSD). The suitability of the RSD depends on its orthogonally, ratability, and uniform precision [112]. Secondly, the empirical model is then developed; it is approximated by a polynomial equation that accounts for elements that consist of powers and cross-product powers, constant coefficients referred to as parameters, and a random experimental error. Albeit empirical, first-degree and second-degree polynomial equations are usually used to fit observations and carry out the optimization. To this end, every model and its reliability depends on the RSD, i.e., first-order designs are used to fit observations with the first-degree models, and observations out of second-order designs are fitted with second-degree models [111][112][113]. The most common first-order designs are 2k factorial, Plackett–Burman, and simplex designs, while the most common second-order designs are 3k factorial, central composite, and the Box–Behnken designs. Note that the choice of a proper RSD is essential since the quality of prediction, as measured by the size of the prediction variance, depends on it; thus, the lower the variance, the better the fit of the responses. On this basis, a single RSD is not able to satisfy all criteria, but it is considered as robust if it meets the assumptions related to the model and the error distribution [111][112]. Finally, the assessing of the results uses both statistical tests, i.e., F-value, t-value, and confidence interval, and graphical tests, i.e., variance dispersion graphs, fraction of design space plots, and quantile plots. Graphical methods [108][109] based on quantile dispersions have also been used to compare experimental designs for estimating variance components in an analysis of variance (ANOVA) situation. RSM can lead to the identification of the operational window where CSC presents its higher yields to PDSM, which, in turn, will be essential in the conceptual design and scaling up of the bioreactor configuration.
Because of the advent of computation in the last years, the bioreactor design not only depends on empirical, but also deterministic approaches, which allows the proper determination of hydraulics, fluid dynamics, mass transport, heat transfer, radiative transfer, and kinetics from different bioreactor configurations at various scales. This information is transferred to design and scale up the industrial bioreactor. The design of this reactor strongly depends on the development of a model coupling kinetics and transport phenomena at both the cell and bioreactor level, including the fluid and the gas phase. This is, however, a complex task, since it needs experiments and mathematical solutions that are not trivial. It is worth stressing that, during the construction of this model, fluid dynamics are yet the bottleneck during the scaling up of a bioreactor configuration because of their impact on transport phenomena, kinetics, and, hence, on the global production of PDSM.
Based on the above, a model accounting for kinetic, deactivation, and all transport mechanisms should be developed from the laboratory to the bench scale. This model should be constructed following a framework based on computational fluid dynamics (CFD). The model needs to be validated at the bench scale before using it to design the industrial bioreactor. The preliminary dimensions of the reactor need to be obtained from the utilization of the practical know-how reported in the literature or experimental and modeling results obtained at the bench scale. It will make the scaling up process more efficient and reliable. Developing a model for the use of CFD allows the consideration of fluid dynamics along with its effect on transport phenomena, which leads to obtaining operating conditions where mixing, hydrodynamics, and transport phenomena are improved without affecting the operating cost of the process. A criterion when designing the industrial-scale bioreactor is to achieve a compromise between operating expenses and yield of the PDSM. At the end of the scaling-up process, the experimentation and investment cost as that compared using an empirical or heuristic approach will be significantly minimized.
In addition to the aforementioned, the scaling up of CSC becomes more challenging when observing how operating conditions impact on the production of PDSM. Operating conditions influence in different scenarios and magnitudes the performance of cell cultures during the production of PDSM, from the supply of nutrients (oxygen, light, ionic strength, pH) to the implementation of mechanical and pneumatic work to keep the process operating in optimal conditions. In further sections, a discussion about the main operating variables in bioreactors and their effect on the performance of cell culture will be provided.

References

  1. Kwon, Y.-W.; Lee, S.-H.; Kim, A.-R.; Kim, B.J.; Park, W.-S.; Hur, J.; Jang, H.; Yang, H.-M.; Cho, H.-J.; Kim, H.-S. Plant callus-derived shikimic acid regenerates human skin through converting human dermal fibroblasts into multipotent skin-derived precursor cells. Stem Cell Res. Ther. 2021, 12, 346.
  2. Furusaki, S.; Takeda, T. Bioreactors for plant cell culture. Compr. Biotechnol. 2017, 519–530.
  3. Gonçalves, S.; Romano, A. Production of plant secondary metabolites by using biotechnological tools. In Secondary Metabolites, Sources and Applications; IntechOpen: London, UK, 2018.
  4. Isah, T.; Umar, S.; Mujib, A.; Sharma, M.P.; Rajasekharan, P.E.; Zafar, N.; Frukh, A. Secondary metabolism of pharmaceuticals in the plant in vitro cultures: Strategies, approaches, and limitations to achieving higher yield. Plant Cell Tissue Organ Cult. 2018, 132, 239–265.
  5. Prasad, G.D.; Sudina, B.; Janardan, L.; Rajani, S.; Rosario, G.-G.M. Establishment of regenerative callus, cell suspension system, and molecular characterization of Taxus wallichiana Zucc. for the in vitro production of Taxol. J. Appl. Pharm. Sci. 2020, 11, 22–34.
  6. Sharma, K.; Zafar, R. Optimization of methyl jasmonate and β-cyclodextrin for enhanced production of taraxerol and taraxasterol in (Taraxacum officinale Weber) cultures. Plant Physiol. Biochem. 2016, 103, 24–30.
  7. Chastang, T.; Pozzobon, V.; Taidi, B.; Courot, E.; Clément, C.; Pareau, D. Resveratrol production by grapevine cells in fed-batch bioreactor: Experiments and modelling. Biochem. Eng. J. 2018, 131, 9–16.
  8. Jeong, Y.J.; Park, S.H.; Park, S.-C.; Kim, S.; Kim, T.H.; Lee, J.; Kim, S.W.; Ryu, Y.B.; Jeong, J.C.; Kim, C.Y. Induced extracellular production of stilbenes in grapevine cell culture medium by elicitation with methyl jasmonate and stevioside. Bioresour. Bioprocess. 2020, 7, 40643.
  9. Le, K.-C.; Jeong, C.-S.; Lee, H.; Paek, K.-Y.; Park, S.-Y. Ginsenoside accumulation profiles in long- and short-term cell suspension and adventitious root cultures in Panax ginseng. Hortic. Environ. Biotechnol. 2018, 60, 125–134.
  10. Malik, S.; Cusido, R.M.; Mirjalili, M.H.; Moyano, E.; Palazon, J.; Bonfill, M. Production of the anticancer drug taxol in Taxus baccata suspension cultures: A review. Process. Biochem. 2011, 46, 23–34.
  11. Sahakyan, N.; Petrosyan, M.; Trchounian, A. The activity of Alkanna species in vitro culture and intact plant extracts against antibiotic resistant bacteria. Curr. Pharm. Des. 2019, 25, 1861–1865.
  12. Gwon, S.Y.; Ahn, J.; Jung, C.H.; Moon, B.; Ha, T.-Y. Shikonin attenuates hepatic steatosis by enhancing beta oxidation and energy expenditure via AMPK activation. Nutrients 2020, 12, 1133.
  13. Jeziorek, M.; Damianakos, H.; Kawiak, A.; Laudy, A.E.; Zakrzewska, K.; Sykłowska-Baranek, K.; Chinou, I.; Pietrosiuk, A. Bioactive rinderol and cynoglosol isolated from Cynoglossum columnae Ten. in vitro root culture. Ind. Crop. Prod. 2019, 137, 446–452.
  14. Rat, A.; Naranjo, H.D.; Krigas, N.; Grigoriadou, K.; Maloupa, E.; Alonso, A.V.; Schneider, C.; Papageorgiou, V.P.; Assimopoulou, A.N.; Tsafantakis, N.; et al. Endophytic bacteria from the roots of the medicinal plant Alkanna tinctoria Tausch (Boraginaceae): Exploration of plant growth promoting properties and potential role in the production of plant secondary metabolites. Front. Microbiol. 2021, 12, 113.
  15. Fu, J.-Y.; Zhao, H.; Bao, J.-X.; Wen, Z.-L.; Fang, R.-J.; Fazal, A.; Yang, M.-K.; Liu, B.; Yin, T.-M.; Pang, Y.-J.; et al. Establishment of the hairy root culture of Echium plantagineum L. and its shikonin production. 3 Biotech 2020, 10, 429.
  16. Baque, A.; Shiragi, H.K.; Moh, S.-H.; Lee, E.-J.; Paek, K.-Y. Production of biomass and bioactive compounds by adventitious root suspension cultures of Morinda citrifolia (L.) in a liquid-phase airlift balloon-type bioreactor. Vitr. Cell. Dev. Biol. Anim. 2013, 49, 737–749.
  17. Veremeichik, G.; Bulgakov, V.; Shkryl, Y.; Silantieva, S.; Makhazen, D.; Tchernoded, G.; Mischenko, N.; Fedoreyev, S.; Vasileva, E. Activation of anthraquinone biosynthesis in long-cultured callus culture of Rubia cordifolia transformed with the rolA plant oncogene. J. Biotechnol. 2019, 306, 38–46.
  18. Mariadoss, A.; Satdive, R.; Fulzele, D.P.; Ramamoorthy, S.; Zayed, H.; Younes, S.; Rajasekaran, C. Enhanced production of anthraquinones by gamma-irradiated cell cultures of Rubia cordifolia in a bioreactor. Ind. Crop. Prod. 2020, 145, 111987.
  19. Kowalczyk, T.; Sitarek, P.; Toma, M.; Rijo, P.; Domínguez-Martíne, E.; Falcó, I.; Sánchez, G.; Śliwiński, T. Enhanced accumulation of betulinic acid in transgenic hairy roots of Senna obtusifolia growing in the Sprinkle Bioreactor and evaluation of their biological properties in various biological models. Chem. Biodivers. 2021, 18, e2100455.
  20. Açıkgöz, M.A. Effects of sorbitol on the production of phenolic compounds and terpenoids in the cell suspension cultures of Ocimum basilicum L. Biologia 2021, 76, 395–409.
  21. Pandey, P.; Singh, S.; Banerjee, S. Ocimum basilicum suspension culture as resource for bioactive triterpenoids: Yield enrichment by elicitation and bioreactor cultivation. Plant Cell Tissue Organ Cult. 2019, 137, 65–75.
  22. Li, Y.-P.; Tang, D.-B.; Wang, X.-Q.; Wang, M.; Zhang, Q.-F.; Liu, Y.; Shen, B.-Y.; Chen, J.-G.; Yin, Z.-P. Development of Origanum vulgare cell suspension culture to produce polyphenols and the stimulation effect of salicylic acid elicitation and phenylalanine feeding. Biotechnol. Bioprocess Eng. 2021, 26, 456–467.
  23. Gonçalves, S.; Moreira, E.; Grosso, C.; Andrade, P.B.; Valentão, P.; Romano, A. Phenolic profile, antioxidant activity and enzyme inhibitory activities of extracts from aromatic plants used in Mediterranean diet. J. Food Sci. Technol. 2017, 54, 219–227.
  24. Sahraroo, A.; Mirjalili, M.H.; Corchete, P.; Babalar, M.; Moghadam, M.R.F. Establishment and characterization of a Satureja khuzistanica Jamzad (Lamiaceae) cell suspension culture: A new in vitro source of rosmarinic acid. Cytotechnology 2016, 68, 1415–1424.
  25. Sahraroo, A.; Mirjalili, M.H.; Babalar, M.; Zarei, A. Enhancement of rosmarinic acid production by Satureja khuzistanica cell suspensions: Effects of phenylalanine and sucrose. SABRAO J. Breed. Genet. 2018, 50, 25–35.
  26. Smetanska, I. Sustainable Production of Polyphenols and Antioxidants by Plant In Vitro Cultures; Springer: Berlin/Heidelberg, Germany, 2018; ISBN 9783319545998.
  27. Och, A.; Podgórski, R.; Nowak, R. Biological activity of berberine—A summary update. Toxins 2020, 12, 713.
  28. Khan, T.; Krupadanam, D.; Anwar, S.Y. The role of phytohormone on the production of berberine in the calli cultures of an endangered medicinal plant, turmeric (Coscinium fenestratum L.). Afr. J. Biotechnol. 2008, 7, 3244–3246.
  29. Yamada, Y.; Yoshimoto, T.; Yoshida, S.T.; Sato, F. Characterization of the promoter region of biosynthetic enzyme genes involved in Berberine Biosynthesis in Coptis japonica. Front. Plant Sci. 2016, 7, 1352.
  30. Cheung, C.K.-L.; Leksawasdi, N.; Doran, P.M. Bioreactor scale-down studies of suspended plant cell cultures. AIChE J. 2018, 64, 4281–4288.
  31. Tabata, M. Transport and secretion of natural products in plant cell cultures. Planta Med. 1991, 57, S21–S26.
  32. Sato, F.; Yamada, Y. High berberine-producing cultures of coptis japonica cells. Phytochemistry 1984, 23, 281–285.
  33. Hou, M.; Wang, R.; Zhao, S.; Wang, Z. Ginsenosides in Panax genus and their biosynthesis. Acta Pharm. Sin. B 2021, 11, 1813–1834.
  34. Adil, M.; Jeong, B.R. In vitro cultivation of Panax ginseng C.A. Meyer. Ind. Crop. Prod. 2018, 122, 239–251.
  35. Nazir, R.; Kumar, V.; Gupta, S.; Dwivedi, P.; Pandey, D.K.; Dey, A. Biotechnological strategies for the sustainable production of diosgenin from Dioscorea spp. Appl. Microbiol. Biotechnol. 2021, 105, 569–585.
  36. Shaikh, S.; Shriram, V.; Khare, T.; Kumar, V. Biotic elicitors enhance diosgenin production in Helicteres isora L. suspension cultures via up-regulation of CAS and HMGR genes. Physiol. Mol. Biol. Plants 2020, 26, 593–604.
  37. Deshpande, H.A.; Bhalsing, S.R. Isolation and characterization of diosgenin from in vitro cultured tissues of Helicteres isora L. Physiol. Mol. Biol. Plants 2013, 20, 89–94.
  38. Das, A.; Sarkar, S.; Bhattacharyya, S.; Gantait, S. Biotechnological advancements in Catharanthus roseus (L.) G. Don. Appl. Microbiol. Biotechnol. 2020, 104, 4811–4835.
  39. Thakore, D.; Srivastava, A.; Sinha, A.K. Mass production of Ajmalicine by bioreactor cultivation of hairy roots of Catharanthus roseus. Biochem. Eng. J. 2017, 119, 84–91.
  40. Alamgir, A.N.M. Cultivation of herbal drugs, biotechnology, and in vitro production of secondary metabolites, high-value medicinal plants, herbal wealth, and herbal trade. In Therapeutic Use of Medicinal Plants and Their Extracts: Volume 1; Springer: Berlin/Heidelberg, Germany, 2017; pp. 379–452. ISBN 9783319638621.
  41. Changxing, L.; Galani, S.; Hassan, F.-U.; Rashid, Z.; Naveed, M.; Fang, D.; Ashraf, A.; Qi, W.; Arif, A.; Saeed, M.; et al. Biotechnological approaches to the production of plant-derived promising anticancer agents: An update and overview. Biomed. Pharmacother. 2020, 132, 110918.
  42. Kumar, P.; Sharma, P.; Kumar, V.; Kumar, A. Plant resources: In vitro production, challenges and prospects of secondary Metabolites from medicinal plants. Ind. Biotechnol. 2019, 2019, 89–104.
  43. Salehi, M.; Karimzadeh, G.; Naghavi, M.R. Synergistic effect of coronatine and sorbitol on artemisinin production in cell suspension culture of Artemisia annua L. cv. Anamed. Plant Cell Tissue Organ Cult. 2019, 137, 587–597.
  44. Kayani, W.K.; Kiani, B.H.; Dilshad, E.; Mirza, B. Biotechnological approaches for artemisinin production in Artemisia. World J. Microbiol. Biotechnol. 2018, 34, 54.
  45. Kubica, P.; Szopa, A.; Kokotkiewicz, A.; Miceli, N.; Taviano, M.; Maugeri, A.; Cirmi, S.; Synowiec, A.; Gniewosz, M.; Elansary, H.; et al. Production of Verbascoside, Isoverbascoside and Phenolic acids in callus, suspension, and bioreactor cultures of Verbena officinalis and biological properties of biomass extracts. Molecules 2020, 25, 5609.
  46. Süntar, I.; Çetinkaya, S.; Haydaroğlu, Ü.S.; Habtemariam, S. Bioproduction process of natural products and biopharmaceuticals: Biotechnological aspects. Biotechnol. Adv. 2021, 50, 107768.
  47. Yue, W.; Ming, Q.-L.; Lin, B.; Rahman, K.; Zheng, C.-J.; Han, T.; Qin, L.-P. Medicinal plant cell suspension cultures: Pharmaceutical applications and high-yielding strategies for the desired secondary metabolites. Crit. Rev. Biotechnol. 2016, 36, 215–232.
  48. Eibl, R.; Meier, P.; Stutz, I.; Schildberger, D.; Hühn, T.; Eibl, D. Plant cell culture technology in the cosmetics and food industries: Current state and future trends. Appl. Microbiol. Biotechnol. 2018, 102, 8661–8675.
  49. Valdiani, A.; Hansen, O.K.; Nielsen, U.B.; Johannsen, V.K.; Shariat, M.; Georgiev, M.I.; Omidvar, V.; Ebrahimi, M.; Dinanai, E.T.; Abiri, R. Bioreactor-based advances in plant tissue and cell culture: Challenges and prospects. Crit. Rev. Biotechnol. 2018, 39, 20–34.
  50. Ochoa-Villarreal, M.; Howat, S.; Hong, S.; Jang, M.O.; Jin, Y.-W.; Lee, E.-K.; Loake, G.J. Plant cell culture strategies for the production of natural products. BMB Rep. 2016, 49, 149–158.
  51. Bhaskar, R.; Xavier, L.S.E.; Udayakumaran, G.; Kumar, D.S.; Venkatesh, R.; Nagella, P. Biotic elicitors: A boon for the in-vitro production of plant secondary metabolites. Plant Cell Tissue Organ Cult. 2021, 147, 1–18.
  52. Thakur, M.; Bhattacharya, S.; Khosla, P.K.; Puri, S. Improving production of plant secondary metabolites through biotic and abiotic elicitation. J. Appl. Res. Med. Aromat. Plants 2019, 12, 1–12.
  53. Narayani, M.; Srivastava, S. Elicitation: A stimulation of stress in in vitro plant cell/tissue cultures for enhancement of secondary metabolite production. Phytochem. Rev. 2017, 16, 1227–1252.
  54. Nabi, N.; Singh, S.; Saffeullah, P. Responses of in vitro cell cultures to elicitation: Regulatory role of jasmonic acid and methyl jasmonate: A review. Vitr. Cell. Dev. Biol. Anim. 2021, 57, 341–355.
  55. Khan, T.; Khan, T.; Hano, C.; Abbasi, B.H. Effects of chitosan and salicylic acid on the production of pharmacologically attractive secondary metabolites in callus cultures of Fagonia indica. Ind. Crop. Prod. 2019, 129, 525–535.
  56. Kehie, M.; Kumaria, S.; Tandon, P. Biotechnological enhancement of capsaicin biosynthesis in cell suspension cultures of Naga King Chili (Capsicum chinense Jacq.). Bioprocess Biosyst. Eng. 2016, 39, 205–210.
  57. Schenke, D.; Utami, H.P.; Zhou, Z.; Gallegos, M.-T.; Cai, D. Suppression of UV-B stress induced flavonoids by biotic stress: Is there reciprocal crosstalk? Plant Physiol. Biochem. 2019, 134, 53–63.
  58. Werner, S.; Maschke, R.W.; Eibl, D.; Eibl, R. Bioreactor technology for sustainable production of plant cell-derived products. In Bioprocessing of Plant In Vitro Systems; Springer: Cham, Switzerland, 2018; pp. 413–432.
  59. Lange, B.M. Commercial-scale tissue culture for the production of plant natural products: Successes, failures and outlook. In Biotechnology of Natural Products; Springer: Cham, Switzerland, 2018; pp. 189–218.
  60. Marketwatch. Available online: https://www.marketwatch.com/press-release/paclitaxel-market-size-in-2021-87-cagr-with-top-countries-data-competition-strategies-share-industry-analysis-by-top-manufactures-growth-insights-and-forecasts-to-2026-2021-08-06 (accessed on 8 December 2021).
  61. Frense, D. Taxanes: Perspectives for biotechnological production. Appl. Microbiol. Biotechnol. 2007, 73, 1233–1240.
  62. Espinosa-Leal, C.A.; Puente-Garza, C.A.; García-Lara, S. In vitro plant tissue culture: Means for production of biological active compounds. Planta 2018, 248, 1–18.
  63. Wagner, H.; Stuppner, H.; Schäfer, W.; Zenk, M. Immunologically active polysaccharides of Echinacea purpurea cell cultures. Phytochemistry 1988, 27, 119–126.
  64. DiCosmo, F.; Misawa, M. Plant cell and tissue culture: Alternatives for metabolite production. Biotechnol. Adv. 1995, 13, 425–453.
  65. Giri, A.; Narasu, M.L. Production of podophyllotoxin from Podophyllum hexandrum: A potential natural product for clinically useful anticancer drugs. Cytotechnology 2000, 34, 17–26.
  66. Sasheva, P.; Ionkova, I. Small Cells for Big Ideas: The Cytotoxic Podophyllotoxin and the Long Journey in Discovering Its Biosynthetic Pathway. In Biotechnology and Production of Anti-Cancer Compounds; Federal University of Maranhao: Sao Luis, Brazil, 2017.
  67. Rao, K.; Chodisetti, B.; Gandi, S.; Giri, A.; Kishor, P.B.K. Cadmium chloride elicitation of Abutilon indicum cell suspension cultures for enhanced stigmasterol production. Plant Biosyst. Int. J. Deal. All Asp. Plant Biol. 2021, 155, 1–6.
  68. Ojha, T.; Hu, Q.; Colombo, C.; Wit, J.; van Geijn, M.; van Steenbergen, M.J.; Bagheri, M.; Königs-Werner, H.; Buhl, E.M.; Bansal, R.; et al. Lyophilization stabilizes clinical-stage core-crosslinked polymeric micelles to overcome cold chain supply challenges. Biotechnol. J. 2021, 16, 2000212.
  69. McElroy, C.; Jennewein, S. Taxol® biosynthesis and production: From forests to fermenters. In Biotechnology of Natural Products; Springer: Berlin/Heidelberg, Germany, 2017; pp. 145–185.
  70. Chattopadhyay, S.; Farkya, S.; Srivastava, A.; Bisaria, V.S. Bioprocess considerations for production of secondary metabolites by plant cell suspension cultures. Biotechnol. Bioprocess Eng. 2002, 7, 138–149.
  71. Lee, S.-W.; Kim, Y.-M.; Cho, C.H.; Kim, Y.T.; Kim, S.M.; Hur, S.Y.; Kim, J.-H.; Kim, B.-G.; Kim, S.-C.; Ryu, H.-S.; et al. An open-label, randomized, parallel, phase ii trial to evaluate the efficacy and safety of a cremophor-free polymeric micelle formulation of paclitaxel as first-line treatment for ovarian cancer: A Korean gynecologic oncology group study (KGOG-3021). Cancer Res. Treat. 2018, 50, 195–203.
  72. Muranaka, T.; Ohkawa, H.; Yamada, Y. Continuous production of scopolamine by a culture of Duboisia leichhardtii hairy root clone in a bioreactor system. Appl. Microbiol. Biotechnol. 1993, 40, 219–223.
  73. D’Amelia, V.; Docimo, T.; Crocoll, C.; Rigano, M. Specialized metabolites and valuable molecules in crop and medicinal plants: The evolution of their use and strategies for their production. Genes 2021, 12, 936.
  74. Singh, J.; Kaushik, N.; Biswas, S. Bioreactors—Technology & design analysis. Scitech J. 2014, 1, 28–36.
  75. Esperança, M.N.; Mendes, C.E.; Rodriguez, G.Y.; Cerri, M.O.; Béttega, R.; Badino, A.C. Sparger design as key parameter to define shear conditions in pneumatic bioreactors. Biochem. Eng. J. 2020, 157, 107529.
  76. Barragán, L.P.; Figueroa, J.; Durán, L.R.; González, C.A.; Hennigs, C. Fermentative Production Methods; Elsevier: Amsterdam, The Netherlands, 2016; pp. 189–217.
  77. Zhang, T.; We, C.; Ren, Y.; Feng, C.; Wu, H. Advances in airlift reactors: Modified design and optimization of operation conditions. Rev. Chem. Eng. 2017, 33, 163–182.
  78. Kumar, N.; Gupta, R.; Bansal, A. Effect of surface tension on hydrodynamics and mass transfer coefficient in airlift reactors. Chem. Eng. Technol. 2020, 43, 995–1004.
  79. Tervasmäki, P.; Latva-Kokko, M.; Taskila, S.; Tanskanen, J. Effect of oxygen transfer on yeast growth—Growth kinetic and reactor model to estimate scale-up effects in bioreactors. Food Bioprod. Process. 2018, 111, 129–140.
  80. Fitzpatrick, J.J. Insights from mathematical modelling into energy requirement and process design of continuous and batch stirred tank aerobic bioreactors. ChemEngineering 2019, 3, 65.
  81. Ahmadi-Sakha, S.; Sharifi, M.; Niknam, V. Bioproduction of phenylethanoid glycosides by plant cell culture of Scrophularia striata Boiss.: From shake-flasks to bioreactor. Plant Cell Tissue Organ Cult. 2016, 124, 275–281.
  82. Estrada-Zúñiga, M.E.; Cruz-Sosa, F.; Rodriguez-Monroy, M.; Verde-Calvo, J.R.; Vernon-Carter, E.J. Phenylpropanoid production in callus and cell suspension cultures of Buddleja cordata Kunth. Plant Cell Tissue Organ Cult. 2009, 97, 39–47.
  83. Vazquez-Marquez, A.M.; Zepeda-Gómez, C.; Burrola-Aguilar, C.; Bernabé-Antonio, A.; Nieto-Trujillo, A.; Cruz-Sosa, F.; Rodríguez-Monroy, M.; Estrada-Zúñiga, M.E. Effect of stirring speed on the production of phenolic secondary metabolites and growth of Buddleja cordata cells cultured in mechanically agitated bioreactor. Plant Cell Tissue Organ Cult. 2019, 139, 155–166.
  84. Busto, V.; Rodriguez-Talou, J.; Giulietti, A.; Merchuk, J. Effect of shear stress on Anthraquinones production by Rubia tinctorum suspension cultures. Biotechnol. Prog. 2008, 24, 175–181.
  85. Gupta, K.; Garg, S.; Singh, J.; Kumar, M. Enhanced production of napthoquinone metabolite (shikonin) from cell suspension culture of Arnebia sp. and its up-scaling through bioreactor. 3 Biotech 2014, 4, 263–273.
  86. Khojasteh, A.; Mirjalili, M.H.; Palazon, J.; Eibl, R.; Cusido, R.M. Methyl jasmonate enhanced production of rosmarinic acid in cell cultures of Satureja khuzistanicain a bioreactor. Eng. Life Sci. 2016, 16, 740–749.
  87. Lambert, C.; Lemaire, J.; Auger, H.; Guilleret, A.; Reynaud, R.; Clément, C.; Courot, E.; Taidi, B. Optimize, modulate, and scale-up resveratrol and resveratrol dimers bioproduction in Vitis labrusca L. Cell suspension from Flasks to 20 L Bioreactor. Plants 2019, 8, 567.
  88. Rani, A.; Meghana, R.; Kush, A. Squalene production in the cell suspension cultures of Indian sandalwood (Santalum album L.) in shake flasks and air lift bioreactor. Plant Cell Tissue Organ Cult. 2018, 135, 155–167.
  89. Salehi, M.; Farhadi, S.; Moieni, A.; Safaie, N.; Ahmadi, H. Mathematical modeling of growth and paclitaxel biosynthesis in Corylus avellana cell culture responding to fungal elicitors using multilayer perceptron-genetic algorithm. Front. Plant Sci. 2020, 11, 1148.
  90. Maschke, R.; Geipel, K.; Bley, T. Modeling of plant in vitro cultures: Overview and estimation of biotechnological processes. Biotechnol. Bioeng. 2014, 112, 1–12.
  91. Villegas, A.; Arias, J.P.; Aragón, D.; Ochoa, S.; Arias, M. Structured model and parameter estimation in plant cell cultures of Thevetia peruviana. Bioprocess Biosyst. Eng. 2016, 40, 573–587.
  92. Chattopadhyay, S.; Bisaria, V.S.; Srivastava, A.K. Enhanced production of Podophyllotoxin by Podophyllum hexandrum using in situ cell retention bioreactor. Biotechnol. Prog. 2003, 19, 1026–1028.
  93. Prakash, G.; Srivastava, A.K. Modeling of azadirachtin production by Azadirachta indica and its use for feed forward optimization studies. Biochem. Eng. J. 2006, 29, 62–68.
  94. Amdoun, R.; Khelifi, L.; Khelifi-Slaoui, M.; Amroune, S.; Benyoussef, E.-H.; Thi, D.V.; Assaf-Ducrocq, C.; Gontier, E. Influence of minerals and elicitation on Datura stramonium L. tropane alkaloid production: Modelization of the in vitro biochemical response. Plant Sci. 2009, 177, 81–87.
  95. Thakore, D.; Srivastava, A.K.; Sinha, A.K. Model based fed batch cultivation and elicitation for the overproduction of ajmalicine from hairy roots of Catharanthus roseus. Biochem. Eng. J. 2015, 97, 73–80.
  96. Salehi, M.; Farhadi, S.; Moieni, A.; Safaie, N.; Hesami, M. A hybrid model based on general regression neural network and fruit fly optimization algorithm for forecasting and optimizing paclitaxel biosynthesis in Corylus avellana cell culture. Plant Methods 2021, 17, 13.
  97. Villadsen, J.; Nielsen, J.; Lidén, G. Chemicals from metabolic pathways. In Bioreaction Engineering Principles; Springer: Boston, MA, USA, 2011; pp. 7–62. ISBN 97814419968792.
  98. Melgarejo-Torres, R.; Castillo-Araiza, C.O.; López-Ordaz, P.; Torres-Martínez, D.; Gutiérrez-Rojas, M.; Lye, G.; Huerta-Ochoa, S. Kinetic mathematical model for ketone bioconversion using Escherichia coli TOP10 pQR239. Chem. Eng. J. 2014, 240, 1–9.
  99. Palmerín-Carreño, D.; Castillo-Araiza, C.; Rutiaga-Quiñones, O.; Verde-Calvo, J.; Huerta-Ochoa, S. Kinetic, oxygen mass transfer and hydrodynamic studies in a three-phase stirred tank bioreactor for the bioconversion of (+)-valencene on Yarrowia lipolytica 2.2ab. Biochem. Eng. J. 2016, 113, 37–46.
  100. Castillo-Araiza, C.; Palmerín-Carreño, D.; Prado-Barragán, A.; Huerta-Ochoa, S. On the conceptual design of a partitioning technology for the bioconversion of (+)-valencene to (+)-nootkatone on whole cells: Experimentation and modelling. Chem. Eng. Process. Process. Intensif. 2017, 122, 493–507.
  101. Liu, Y. A simple thermodynamic approach for derivation of a general Monod equation for microbial growth. Biochem. Eng. J. 2006, 31, 102–105.
  102. Liu, Y. Overview of some theoretical approaches for derivation of the Monod equation. Appl. Microbiol. Biotechnol. 2007, 73, 1241–1250.
  103. Wang, J.D.; Levin, P.A. Metabolism, cell growth and the bacterial cell cycle. Nat. Rev. Genet. 2009, 7, 822–827.
  104. Henson, A.M. Dynamic modeling of microbial cell populations. Curr. Opin. Biotechnol. 2003, 14, 460–467.
  105. Daugulis, A.J. Partitioning bioreactors. Curr. Opin. Biotechnol. 1997, 8, 169–174.
  106. Kalil, S.; Maugeri, F.; Rodrigues, M. Response surface analysis and simulation as a tool for bioprocess design and optimization. Process. Biochem. 2000, 35, 539–550.
  107. Ríos-Morales, D.; Castillo-Araiza, C.O.; Vizcarra-Mendoza, M.G. Study of the agglomeration mechanism of a natural organic solid in a bench-scale wet fluidized bed using statistical analysis and discretized population balance. Chem. Eng. Commun. 2014, 201, 23–40.
  108. Khuri, A.I.; Mukhopadhyay, S. Response surface methodology. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 128–149.
  109. Dellino, G.; Kleijnen, J.P.; Meloni, C. Robust optimization in simulation: Taguchi and response surface methodology. Int. J. Prod. Econ. 2010, 125, 52–59.
  110. Anderson-Cook, C.M.; Borror, C.M.; Montgomery, D.C. Response surface design evaluation and comparison. J. Stat. Plan. Inference 2009, 139, 629–641.
  111. Montgomery, D.C. Design and Analysis of Experiments; John Wiley: Hoboken, NJ, USA, 2013; ISBN 9781118146927.
  112. Box, G. JS hunter, WG hunter. Stat. Exp. Des. Innov. Discov. 2005, 21, 303–304.
  113. Hanrahan, G.; Lu, K. Application of factorial and response surface methodology in modern experimental design and optimization. Crit. Rev. Anal. Chem. 2006, 36, 141–151.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Biotechnology & Applied Microbiology
Contributor MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Francisco Cruz-Sosa
View Times: 1.9K
Entry Collection: Biopharmaceuticals Technology
Revisions: 2 times (View History)
Update Date: 29 Dec 2021
Table of Contents
    1000/1000
    Hot Most Recent
    Feedback