Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Mahdi Aghaabbasi
 + 1322 word(s) 1322 2021-12-15 07:54:48 |
2 The format is correct.
Yvaine Wei
 Meta information modification 1322 2021-12-23 09:35:45 |

Video Upload Options

Do you have a full video?
Send video materials Upload full video

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Aghaabbasi, M. Classifying Travel Mode Choice through Adjustable SVM Model. Encyclopedia. Available online: https://encyclopedia.pub/entry/17491 (accessed on 08 May 2024).
Aghaabbasi M. Classifying Travel Mode Choice through Adjustable SVM Model. Encyclopedia. Available at: https://encyclopedia.pub/entry/17491. Accessed May 08, 2024.
Aghaabbasi, Mahdi. "Classifying Travel Mode Choice through Adjustable SVM Model" Encyclopedia, https://encyclopedia.pub/entry/17491 (accessed May 08, 2024).
Aghaabbasi, M. (2021, December 23). Classifying Travel Mode Choice through Adjustable SVM Model. In Encyclopedia. https://encyclopedia.pub/entry/17491
Aghaabbasi, Mahdi. "Classifying Travel Mode Choice through Adjustable SVM Model." Encyclopedia. Web. 23 December, 2021.
Classifying Travel Mode Choice through Adjustable SVM Model
Edit
This entry is adapted from the peer-reviewed paper 10.3390/app112411916

The investigation of travel mode choice is an essential task in transport planning and policymaking for predicting travel demands. Typically, mode choice datasets are imbalanced and learning from such datasets is challenging. This study deals with imbalanced mode choice data by developing an algorithm (SVMAK) based on a support vector machine model and the theory of adjusting kernel scaling.

imbalanced data travel mode choice data machine learning SVM

1. Introduction

A considerable amount of people’s daily trips is associated with their work. Transport planners and engineers attempt to discover work-related travel behaviors and establish strategies for reducing the adverse impacts of motorized transport on traffic, health, and the environment. One of these important behaviors is work mode choice which refers to the process where an individual chooses a certain mode for his/her trip to work. According to the literature, a variety of factors influence the work mode choice. Socioeconomic factors [1][2][3], household attributes e.g., [4], trip characteristics e.g., [5], job e.g., [6][7][8][9], and built environment [2][10][11] are some of these factors [3][11].
Mode choice data include a wide range of variables and samples. Typically, these data are complex and incomplete [12]. Furthermore, since motorized transport is dominant in most parts of the world, the travel surveys yield unbalanced mode choice classes; that is, there are more people who use cars than people who use other commute modes.
To date, many studies investigated the choice of travel mode to work (Table 1). These methods employed both traditional statistical methods and machine learning (ML) techniques. However, the former is criticized because of its linearity assumptions concerning mode choice data [13][14][15]. Thus, the employment of ML techniques has receieved more attention recently [16][17][18][19][20][21][22][23]. The classification of the new cases established concerning the existing samples is an essential task in ML models. If at least one of the categories comprises a smaller number of samples than other categories, the classification process becomes complex [24]. The class imbalance issue is simply an uneven data distribution amongst the different categories of the target. The precision of the classification algorithms will be unreliable when they are influenced by the majority class. In this case, the new samples are distributed to the majority category since the classification model tends to predict the minority category with less accuracy, which is an undesirable consequence [25].
Support vector machine (SVM) is a renowned ML technique for classification [26]. This algorithm also was used as a base to cope with imbalanced data. Batuwita and Palade [27] developed the fuzzy SVM model and dealt with imbalanced data in the presence of noises and outliers. Wang and Japkowicz [28] suggested boosting-SVMs with asymmetric cost. Their model runs by adjusting the classifier utilizing cost assignation, though it compensates the bias presented with adjustment through utilizing a combination system that is comparable, in effect, to adjust the distribution of data. Wu and Chang [29] suggested the class-boundary alignment algorithm to augment the SVM model to deal with imbalanced data. They modified the class boundary by converting the kernel function if data is represented in a vector space. This modification can also be performed by adjusting the kernel matrix if the data do not possess a vector-space representation. To enhance forecast performance, Liu et al. [30] suggested consolidating an integrated sampling system, which mixes both over-sampling and under-sampling, with an ensemble of SVM. These studies investigated the binary classification problem based on the SVM model; however, less examinations have been done concerning multiclass imbalanced classification based on this model.
Many studies in other domains, including medicine, economy, crash severity, and so on, tried to reduce the issues of imbalanced data, e.g., [31][32][33]. However, a very small number of studies have investigated the issues of imbalanced travel mode choice data and proposed a solution for it [33].
Table 1. Some investigation on work mode choice.
Author Main Factors Used Modelling Method
Lu and Kawamura [34] Mode preferences and responsiveness to level-of-service Multinomial logit
Badoe [4] Households (two-workers) Multinomial logit
Xie et al. [35] Sociodemographic and Level-of-service attributes Multinomial logit, Decision trees (DT), and Neural Networks (NN)
Patterson et al. [36] Gender Multinomial logit
Al-Ahmadi [37] Cultural, socioeconomic, safety, and religious parameters Disaggregate models and utility maximization
Gang [1] Socioeconomic Multinomial logit
Vega and Reynolds-Feighan [5] Travel time, travel cost, and employment destinations Binary logit and GIS
Vega and Reynolds-Feighan [38] Central and non-central and suburban employment patterns. GIS and Cross-Nested Logit (CNL)
Day, Habib and Miller [6] Commuter trip timing, occupation groups, labor rates, work hour rules, free parking availability, and the spatial distribution of work locations Multinomial logit
Habib [7] Work start time and work duration Multinomial logit
Heinen, Maat and van Wee [8] Office culture and colleagues’ and employers’ attitudes Binary logit
Hamre and Buehler [9] free car parking, public transportation benefits, showers/lockers, and bike parking at work Multinomial logit
Heinen and Bohte [39] Attitudes Toward Mode Choice Multinomial logit
Tran, Zhang, Chikaraishi and Fujiwara [10] Neighborhood and travel preferences, land use policy, land use diversity and population density Multinomial logit
Kunhikrishnan and Srinivasan [40] Contextual heterogeneity Binary logit
Franco [41] Downtown parking supply Spatial general equilibrium
model
Simons, De Bourdeaudhuij, Clarys, De Geus, Vandelanotte, Van Cauwenberg and Deforche [2] Gender, socio-economic-status (SES) and living environment (urban vs. rural) Zero-inflated negative binomial (ZINB) regression
Indriany et al. [42] Risk and uncertainty Binomial logit
Irfan et al. [43] Econometric Modeling Multinomial logit
Hatamzadeh et al. [44] Gender Binary logit

2. Sensitivity Analysis

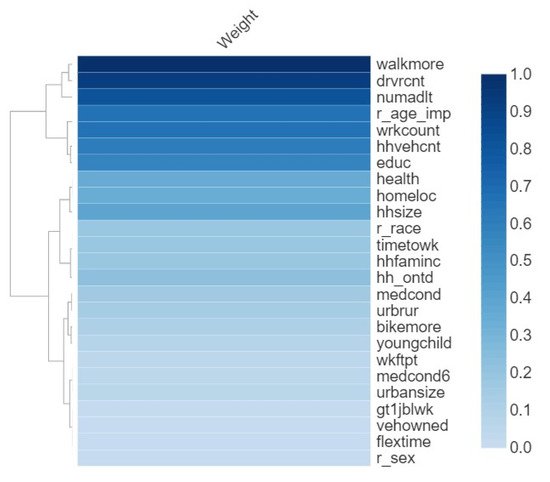
Many factors impact the travel mode choice; however, their effects are not the same. Thus, it is necessary to ascertain the magnitude of these impacts and identify the most influential factors on travel mode choice. For this purpose, the mutual information (MI) test method was employed[45], which computes the importance of the inputs. MI means a filtering system that captures the random association between inputs and the target. MI examines the dependence among variables and confirms the strength of the connection among them. 

Ultimately, the importance magnitude of each attribute for predicting travel mode choice was achieved based on the scores obtained in the MI test. The outcomes of this analysis are shown in Figure 1. The most important attributes were reason for not walking (walkmore), number of drivers in household (drvcnet), and count of adult household members at least 18 years old (numadlt). On the other hands, the lowest scores belonged to flexibility of work start time (flextime), owned vehicle longer than a year (vehowned), and gender (r_sex).
Applsci 11 11916 g004 550
Figure 1. Outcomes of sensitivity analysis.
Reasons for not walking among respondents included unsafe street crossings, heavy traffic, and insufficient night lighting. It is clear that any improvement in these street conditions can encourage people to shift from motorized transport to walking. Thus, it makes sense that this factor is among the most influential travel mode choice factors to work [46][47][48]. The significance of the number of drivers in households can be attributed to its influence on the usage of vehicles and the generation of more trips. In practice, the likelihood of choosing active transportation options reduces as the number of drivers in a family grows [49]. As the number of adults in a family increases, the need for independent trips rises. Because of the different responsibilities that each adult in the family has, it is not easy to consolidate trips into one trip. This can be easily one of the principal sources of more trip generation and use of motorized transportation.
The flexibility of work start time was among the least important factors. This could be attributable to work culture of the respondents in the US. However, several previous studies showed that the flexibility of work start time influences the mode choice e.g., [49][50]. The possession of a vehicle for longer than a year was also an unimportant factor for predicting the choice of travel mode to work. A possible reason for this is that people usually look for flexible and convenient travel options to work. Usually, they are reluctant to replace their private cars with healthy travel modes unless they face new challenges. These challenges can be health problems, heavy traffic, so on. Thus, it is sensible that this factor does not influence the mode choice substantially.

References

  1. Gang, L. A behavioral model of work-trip mode choice in Shanghai. China Econ. Rev. 2007, 18, 456–476.
  2. Simons, D.; De Bourdeaudhuij, I.; Clarys, P.; De Geus, B.; Vandelanotte, C.; Van Cauwenberg, J.; Deforche, B. Choice of transport mode in emerging adulthood: Differences between secondary school students, studying young adults and working young adults and relations with gender, SES and living environment. Transp. Res. Part A Policy Pract. 2017, 103, 172–184.
  3. Ali, M.; de Azevedo, A.R.G.; Marvila, M.T.; Khan, M.I.; Memon, A.M.; Masood, F.; Almahbashi, N.M.Y.; Shad, M.K.; Khan, M.A.; Fediuk, R.; et al. The Influence of COVID-19-Induced Daily Activities on Health Parameters—A Case Study in Malaysia. Sustainability 2021, 13, 7465.
  4. Badoe, D. Modelling work-trip mode choice decisions in two-worker households. Transp. Plan. Technol. 2002, 25, 49–73.
  5. Vega, A.; Reynolds-Feighan, A. Employment sub-centres and travel-to-work mode choice in the Dublin region. Urban Stud. 2008, 45, 1747–1768.
  6. Day, N.; Habib, K.N.; Miller, E.J. Analysis of work trip timing and mode choice in the Greater Toronto Area. Can. J. Civ. Eng. 2010, 37, 695–705.
  7. Habib, K.M.N. Modeling commuting mode choice jointly with work start time and work duration. Transp. Res. Part A Policy Pract. 2012, 46, 33–47.
  8. Heinen, E.; Maat, K.; van Wee, B. The effect of work-related factors on the bicycle commute mode choice in the Netherlands. Transportation 2013, 40, 23–43.
  9. Hamre, A.; Buehler, R. Commuter mode choice and free car parking, public transportation benefits, showers/lockers, and bike parking at work: Evidence from the Washington, DC region. J. Public Transp. 2014, 17, 4.
  10. Tran, M.T.; Zhang, J.; Chikaraishi, M.; Fujiwara, A. A joint analysis of residential location, work location and commuting mode choices in Hanoi, Vietnam. J. Transp. Geogr. 2016, 54, 181–193.
  11. Ali, M.; Dharmowijoyo, D.B.; Harahap, I.S.; Puri, A.; Tanjung, L.E. Travel behaviour and health: Interaction of Activity-Travel Pattern, Travel Parameter and Physical Intensity. Solid State Technol. 2020, 63, 4026–4039.
  12. Aghaabbasi, M.; Shekari, Z.A.; Shah, M.Z.; Olakunle, O.; Armaghani, D.J.; Moeinaddini, M. Predicting the use frequency of ride-sourcing by off-campus university students through random forest and Bayesian network techniques. Transp. Res. Part A Policy Pract. 2020, 136, 262–281.
  13. Stylianou, K.; Dimitriou, L.; Abdel-Aty, M. Big data and road safety: A comprehensive review. Mobil. Patterns Big Data Transp. Anal. 2019, 297–343.
  14. Rashidi, S.; Ranjitkar, P.; Hadas, Y. Modeling bus dwell time with decision tree-based methods. Transp. Res. Rec. 2014, 2418, 74–83.
  15. Ali, M.; Dharmowijoyo, D.B.E.; de Azevedo, A.R.G.; Fediuk, R.; Ahmad, H.; Salah, B. Time-Use and Spatio-Temporal Variables Influence on Physical Activity Intensity, Physical and Social Health of Travelers. Sustainability 2021, 13, 12226.
  16. Parsajoo, M.; Armaghani, D.J.; Mohammed, A.S.; Khari, M.; Jahandari, S. Tensile strength prediction of rock material using non-destructive tests: A comparative intelligent study. Transp. Geotech. 2021, 31, 100652.
  17. Harandizadeh, H.; Armaghani, D.J.; Asteris, P.G.; Gandomi, A.H. TBM performance prediction developing a hybrid ANFIS-PNN predictive model optimized by imperialism competitive algorithm. Neural Comput. Appl. 2021, 33, 16149–16179.
  18. Li, E.; Zhou, J.; Shi, X.; Armaghani, D.J.; Yu, Z.; Chen, X.; Huang, P. Developing a hybrid model of salp swarm algorithm-based support vector machine to predict the strength of fiber-reinforced cemented paste backfill. Eng. Comput. 2020, 37, 1–22.
  19. Jahed Armaghani, D.; Kumar, D.; Samui, P.; Hasanipanah, M.; Roy, B. A novel approach for forecasting of ground vibrations resulting from blasting: Modified particle swarm optimization coupled extreme learning machine. Eng. Comput. 2021, 37, 3221–3235.
  20. Armaghani, D.J.; Harandizadeh, H.; Momeni, E.; Maizir, H.; Zhou, J. An optimized system of GMDH-ANFIS predictive model by ICA for estimating pile bearing capacity. Artif. Intell. Rev. 2021, 54, 1–38.
  21. Li, Z.; Yazdani Bejarbaneh, B.; Asteris, P.G.; Koopialipoor, M.; Armaghani, D.J.; Tahir, M. A hybrid GEP and WOA approach to estimate the optimal penetration rate of TBM in granitic rock mass. Soft Comput. 2021, 25, 11877–11895.
  22. Yu, C.; Koopialipoor, M.; Murlidhar, B.R.; Mohammed, A.S.; Armaghani, D.J.; Mohamad, E.T.; Wang, Z. Optimal ELM–Harris Hawks optimization and ELM–Grasshopper optimization models to forecast peak particle velocity resulting from mine blasting. Nat. Resour. Res. 2021, 30, 2647–2662.
  23. Menardi, G.; Torelli, N. Training and assessing classification rules with imbalanced data. Data Min. Knowl. Discov. 2014, 28, 92–122.
  24. Daskalaki, S.; Kopanas, I.; Avouris, N. Evaluation of classifiers for an uneven class distribution problem. Appl. Artif. Intell. 2006, 20, 381–417.
  25. Vapnik, V. The Nature of Support Vector Machine; Springer: Berlin/Heidelberg, Germany, 1999.
  26. Batuwita, R.; Palade, V. FSVM-CIL: Fuzzy Support Vector Machines for Class Imbalance Learning. IEEE Trans. Fuzzy Syst. 2010, 18, 558–571.
  27. Wang, B.X.; Japkowicz, N. Boosting support vector machines for imbalanced data sets. Knowl. Inf. Syst. 2009, 25, 1–20.
  28. Wu, G.; Chang, E.Y. Class-Boundary Alignment for Imbalanced Dataset Learning. In Proceedings of the Workshop Learningfrom Imbalanced Datasets II, Washington, DC, USA, 21 August 2003; pp. 49–56.
  29. Liu, Y.; Yu, X.; Huang, J.X.; An, A. Combining integrated sampling with SVM ensembles for learning from imbalanced datasets. Inf. Process. Manag. 2011, 47, 617–631.
  30. Liu, Z.; Tang, D.; Cai, Y.; Wang, R.; Chen, F. A hybrid method based on ensemble WELM for handling multi class imbalance in cancer microarray data. Neurocomputing 2017, 266, 641–650.
  31. Hordri, N.F.; Yuhaniz, S.S.; Azmi, N.F.M.; Shamsuddin, S.M. Handling class imbalance in credit card fraud using resampling methods. Int. J. Adv. Comput. Sci. Appl. 2018, 9, 390–396.
  32. Kim, S.; Lym, Y.; Kim, K.-J. Developing crash severity model handling class imbalance and implementing ordered nature: Focusing on elderly drivers. Int. J. Environ. Res. Public Health 2021, 18, 1966.
  33. Rezaei, S.; Khojandi, A.; Haque, A.M.; Brakewood, C.; Jin, M.; Cherry, C. Performance evaluation of mode choice models under balanced and imbalanced data assumptions. Transp. Lett. 2021, 13, 1–13.
  34. Lu, Y.; Kawamura, K. Data-mining approach to work trip mode choice analysis in Chicago, Illinois, area. Transp. Res. Rec. 2010, 2156, 73–80.
  35. Xie, C.; Lu, J.; Parkany, E. Work travel mode choice modeling with data mining: Decision trees and neural networks. Transp. Res. Rec. 2003, 1854, 50–61.
  36. Patterson, Z.; Ewing, G.; Haider, M. Gender-based analysis of work trip mode choice of commuters in suburban Montreal, Canada, with stated preference data. Transp. Res. Rec. 2005, 1924, 85–93.
  37. Al-Ahmadi, H. Development of intercity work mode choice model for Saudi Arabia. In WIT Transactions on The Built Environment; WITT Press: Southampton, UK, 2007; Volume 96.
  38. Vega, A.; Reynolds-Feighan, A. A methodological framework for the study of residential location and travel-to-work mode choice under central and suburban employment destination patterns. Transp. Res. Part A Policy Pract. 2009, 43, 401–419.
  39. Heinen, E.; Bohte, W. Multimodal commuting to work by public transport and bicycle: Attitudes toward mode choice. Transp. Res. Rec. 2014, 2468, 111–122.
  40. Kunhikrishnan, P.; Srinivasan, K.K. Choice set variability and contextual heterogeneity in work trip mode choice in Chennai city. Transp. Lett. 2019, 11, 174–189.
  41. Franco, S.F. Downtown parking supply, work-trip mode choice and urban spatial structure. Transp. Res. Part B Methodol. 2017, 101, 107–122.
  42. Indriany, S.; Sjafruddin, A.; Kusumawati, A.; Weningtyas, W. Mode choice model for working trip under risk and uncertainty. In Proceedings of the AIP Conference Proceedings, Maharashtra, India, 5–6 July 2018; p. 020041.
  43. Irfan, M.; Khurshid, A.N.; Khurshid, M.B.; Ali, Y.; Khattak, A. Policy implications of work-trip mode choice using econometric modeling. J. Transp. Eng. Part A Syst. 2018, 144, 04018035.
  44. Hatamzadeh, Y.; Habibian, M.; Khodaii, A. Walking mode choice across genders for purposes of work and shopping: A case study of an Iranian city. Int. J. Sustain. Transp. 2020, 14, 389–402.
  45. Verron, S.; Tiplica, T.; Kobi, A. Fault detection and identification with a new feature selection based on mutual information. J. Process. Control. 2008, 18, 479–490.
  46. Aghaabbasi, M.; Shah, M.Z.; Zainol, R. Investigating the Use of Active Transportation Modes Among University Employees Through an Advanced Decision Tree Algorithm. Civil. Sustain. Urban. Eng. 2021, 1, 26–49.
  47. Aghaabbasi, M.; Moeinaddini, M.; Shah, M.Z.; Asadi-Shekari, Z. A new assessment model to evaluate the microscale sidewalk design factors at the neighbourhood level. J. Transp. Health 2017, 5, 97–112.
  48. Tabatabaee, S.; Aghaabbasi, M.; Mahdiyar, A.; Zainol, R.; Ismail, S. Measurement Quality Appraisal Instrument for Evaluation of Walkability Assessment Tools Based on Walking Needs. Sustainability 2021, 13, 11342.
  49. Sultana, S. Factors Affecting Parents’ Choice of Active Transport Modes for Children’s Commute to School: Evidence from 2017 NHTS Data; The University of Toledo: Toledo, OH, USA, 2019.
  50. Thorhauge, M.; Cherchi, E.; Rich, J. How flexible is flexible? Accounting for the effect of rescheduling possibilities in choice of departure time for work trips. Transp. Res. Part A Policy Pract. 2016, 86, 177–193.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Transportation
Contributor MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Mahdi Aghaabbasi
View Times: 582
Revisions: 2 times (View History)
Update Date: 24 Dec 2021
Table of Contents
    1000/1000
    Hot Most Recent
    Feedback