Your browser does not fully support modern features. Please upgrade for a smoother experience.

Submitted Successfully!
Thank you for your contribution! You can also upload a video entry or images related to this topic.
For video creation, please contact our Academic Video Service.
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Peishi Yu | + 1237 word(s) | 1237 | 2021-12-10 04:47:30 | | | |
| 2 | Yvaine Wei | -49 word(s) | 1188 | 2021-12-13 02:53:00 | | |
Video Upload Options
We provide professional Academic Video Service to translate complex research into visually appealing presentations. Would you like to try it?
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Yu, P. The Parallel Single-Walled Carbon Nanotubes. Encyclopedia. Available online: https://encyclopedia.pub/entry/17019 (accessed on 14 January 2026).
Yu P. The Parallel Single-Walled Carbon Nanotubes. Encyclopedia. Available at: https://encyclopedia.pub/entry/17019. Accessed January 14, 2026.
Yu, Peishi. "The Parallel Single-Walled Carbon Nanotubes" Encyclopedia, https://encyclopedia.pub/entry/17019 (accessed January 14, 2026).
Yu, P. (2021, December 13). The Parallel Single-Walled Carbon Nanotubes. In Encyclopedia. https://encyclopedia.pub/entry/17019
Yu, Peishi. "The Parallel Single-Walled Carbon Nanotubes." Encyclopedia. Web. 13 December, 2021.
Copy Citation
For small structures on the scale of nanometers, the intermolecular van der Waals (vdW) interaction can play a leading role in some cases. Since their discovery, carbon nanotubes (CNTs) have shown great application prospects in various fields with their excellent physical and mechanical properties.
vdW interaction
cohesive energy
vibration
1. Introduction
The molecular dynamics (MD) simulation software LAMMPS (Large-scale Atomic Molecular Massively Parallel Simulator) [1] has been widely used to predict the remarkable thermomechanical properties of CNTs, such as the influence of grain boundaries on the mechanical properties of polycrystalline carbon nanotubes [2] and the transversely isotropic thermal properties of carbon nanotubes containing vacancies [3][4]. The existing research results show that in a micro system composed of carbon nanotubes (CNTs) bundles, the van der Waals (vdWs) interaction between adjacent carbon tubes has a great impact on the mechanical behavior of the system [5][6][7][8][9][10].
With the influence of finite size and boundary effects, the internal vdW bonding energy has an important impact on the mechanical behavior of CNT bundle micro systems [11][12][13]. Therefore, clarifying the bond energy between tube bundles of finite size has important guiding significance for the design and application of microsystems [14][15][16][17][18][19][20].
In previous work, Zhao et al. obtained the analytical solution of the bonding energy per unit length of infinite parallel single-walled CNTs based on the continuous model, and analyzed the influence of CNT diameter on the bonding energy and the equilibrium distance of the interface [8]. However, due to the limited length of CNTs in actual microsystems, the scale effect of length on the cohesive energy between tubes needs to be further explored.
Zhang et al. [12] prepared suspended single-walled CNT array devices and found that this structure has unique mechanical behavior. Based on the molecular mechanics model, Chang [13] proposed an anisotropic shell model to reveal the mechanical properties of CNTs, and studied the young’s modulus, Poisson’s ratio and radial breathing mode of single-walled CNTs, which laid a foundation for further study of the influence of the bonding energy between parallel carbon tubes on microsystems. Rueckes et al. [21] studied a suspended single-walled CNT array and found that the array has good characteristics of switchable and bi-stable device elements, and the mechanical stability of this structure is determined by the vdW interaction between single-walled CNTs. Wang and Hu further studied the thermodynamic vibration between monolayer graphene sheets based on the nonlocal elastic plate model [22]. Parallel CNT systems have prospective application as micromechanical systems.
For nano-mechanical systems, the shear deformation effect has been studied recently in the literature. Al-Furjan et al. presented the vibrational characteristics of a rotating orthotropic piezoelectric nanodisk [23]. Li et al. analyzed and tested the quasi-static compression and hygrothermal stability of BMI/CE co-cured composite lattice cylindrical shell [24]. Zhang et al. designed and fabricated an ultra-lightweight beam string structure made of carbon fibre-reinforced polymer (CFRP) composites [25]. Dai et al. investigated the vibrations of non-polynomial viscoelastic composite open-type shells under residual stresses [26]. Zhang et al. dealt with the vibration and low-velocity impact responses of functionally graded graphene nanoplatelet-reinforced composite panels on a viscoelastic foundation [27].
2. Quantification of the vdW Interaction between Carbon Atoms
The vdW energy variation with the distance between two carbon atoms is shown in Figure 1. For r < r0, the repulsive force is dominant, defining the repulsive domain, whereas the attractive force is dominant for r > r0, forming the attractive domain. The blue dash, red dot and black solid lines in Figure 1b represent the repulsive, attractive and resultant forces between the two interacting atoms, respectively.

Figure 1. The vdW interaction between atoms: (a) the distribution diagram energy density surrounding the atom; (b) the interaction variation with the distance between two atoms.
3. Cohesive Energy between Two Finite-Length Parallel CNTs
The continuum model and coordinate system of two parallel single-walled CNTs are established as shown in Figure 2a. The radii of the CNTs are r1 and r2 respectively, and the shortest distance between parallel CNTs is h.

Figure 2. The (a) continuum model and coordinate system of two parallel single-walled CNTs and the (b) atom models of the MD simulations.
Molecular dynamics (MD) simulations were conducted using the LAMMPS software package [1] to verify the analytical model, as shown in Figure 2b. The adaptive intermolecular reactive empirical bond order (AIREBO) potential was used [28], which evaluates the covalent carbon–carbon bonding interaction by the well-established REBO potential, and the non-bonded van de Waals interaction was described by the 12-6 Lennard-Jones (LJ) potential (σ = 0.34 nm and ε = 0.0028 eV) [29][30]. ReaxFF was mainly used for the chemical reaction atomic simulations, as the Tersoff potential cannot describe the non-bonded van de Waals interactions between CNTs. The AIREBO potential function with an LJ cut-off radius of 10.2 Å was adopted in all the simulations [31][32]. The Polak–Ribiere version of the conjugated gradient algorithm [33] was used to optimize the initial positions of atoms. The temperature of system was controlled using Nose–Hoover thermal bath coupling [34][35] (coupling constant 0.1 ps, time step 0.5 fs) for 0.5 ns. The time step used in the simulations was set at 0.5 fs.
4. Research on the Vibration Modes for Nano Tubes
For two parallel CNTs with different tube diameters, the vibration frequencies are predicted by the analytical model as shown in Figure 3. The resonance frequency in Figure 3a for low-frequency vibration decreases with the increase in tube diameter. For high-frequency vibration in Figure 3c the resonance frequency reaches the maximum value when r2 = (20,20), which is among the several prediction results including r2 = (5,5)~(50,50). The amplitude ratio in Figure 6b,d show remarkable dependence and significant nonlinearity with the change in the diameters of the two CNTs.


Figure 3. Vibration characteristic of the two parallel CNTs with different diameters: (a) resonance frequency under low frequency, (b) amplitude ratio of CNTs under low frequency, (c) resonance frequency under high frequency, (d) amplitude ratio of CNTs under high frequency.
The influence of vibration modes (takes the first three orders into account) on the resonant frequency for the bi-CNT system with different tube diameters was obtained and is shown in Figure 4. It can be seen from Figure 4a,c that the order has a significant influence on the resonant frequency of carbon nanotubes, which show an increasing tendency in the resonant frequency with the increase in order. The amplitude ratio presents a decreasing dependence on the order, as shown in Figure 4b,d. This confirms that the system is nonlinear because the vdW interaction is nonlinear.
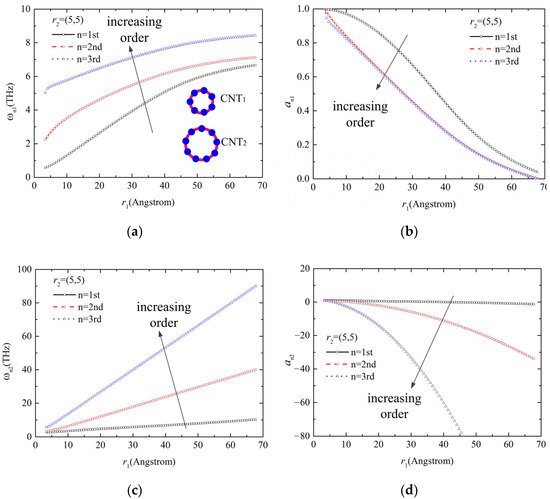
Figure 4. Effect of order on the vibration of CNTs with different diameters: (a) the increasing tendency for the resonant frequency with the increase in order under low frequency, (b) the decreasing dependence of amplitude ratio on the order under low frequency, (c) the increasing tendency for the resonant frequency with the increase in order under high frequency, (d) the decreasing dependence of amplitude ratio on the order under high frequency.
The proposed model focuses on the vibration of CNTs with large slenderness ratios. Thus, the deformation of the cross section is neglected in the continuum beam model. However, if the prerequisite of the large slenderness is not satisfied (for short CNT with large radius), the geometric nonlinearity would be influential on the vibration properties and cannot be neglected. The scope of applications of the continuum mechanics model at the nano scale is always an important topic and has been the subject of many studies in the field [6][8][36].
References
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19.
- Alian, A.R.; Meguid, S.A.; Kundalwal, S.I. Unraveling the influence of grain boundaries on the mechanical properties of poly-crystalline carbon nanotubes. Carbon 2017, 125, 180–188.
- Kothari, R.; Kundalwal, S.I.; Sahu, S.K. Transversely isotropic thermal properties of carbon nanotubes containing vacancies. Acta Mech. 2018, 229, 2787–2800.
- Kundalwal, S.I.; Choyal, V. Transversely isotropic elastic properties of carbon nanotubes containing vacancy defects using MD. Acta Mech. 2018, 229, 2571–2584.
- Carrella, A.; Brennan, M.J.; Waters, T.P. Static analysis of a passive vibration isolator with quasi-zero-stiffness characteristic. J. Sound Vib. 2007, 301, 678–689.
- Ru, C.Q. Effect of van der Waals forces on axial buckling of a double-walled carbon nanotube. J. Appl. Phys. 2000, 87, 7227–7231.
- Ru, C.Q. Axially compressed buckling of a doublewalled carbon nanotube embedded in an elastic medium. J. Mech. Phys. Solids 2001, 49, 1265–1279.
- He, X.Q.; Kitipornchai, S.; Liew, K.M. Buckling analysis of multi-walled carbon nanotubes: A continuum model accounting for van der Waals interaction. J. Mech. Phys. Solids 2005, 53, 303–326.
- Wang, C.Y.; Zhang, Y.Y.; Wang, C.M.; Tan, V.B.C. Buckling of carbon nanotubes: A literature survey. J. Nanosci. Nanotechnol. 2007, 7, 4221–4247.
- Lu, W.B.; Wu, J.; Song, J.; Hwang, K.C.; Jiang, L.Y.; Huang, Y. A cohesive law for interfaces between multi-wall carbon nanotubes and polymers due to the van der Waals interactions. Comput. Methods Appl. Mech. Eng. 2008, 197, 3261–3267.
- Zhao, J.; Jiang, J.-W.; Jia, Y.; Guo, W.; Rabczuk, T. A theoretical analysis of cohesive energy between carbon nanotubes, graphene and substrates. Carbon 2013, 57, 108–119.
- Zhang, J.; Liu, S.; Nshimiyimana, J.P.; Deng, Y.; Hou, G.; Chi, X.; Hu, X.; Zhang, Z.; Wu, P.; Wang, G.; et al. Wafer-Scale fabrication of suspended single-walled carbon nanotube arrays by silver liquid dynamics. Small 2017, 13, 1701218.
- Chang, T. A molecular based anisotropic shell model for single-walled carbon nanotubes. J. Mech. Phys. Solids 2010, 58, 1422–1433.
- Ghabussi, A.; Ashrafi, N.; Shavalipour, A.; Hosseinpour, A.; Habibi, M.; Moayedi, H.; Babaei, B.; Safarpour, H. Free vibration analysis of an electro-elastic GPLRC cylindrical shell surrounded by viscoelastic foundation using modified length-couple stress parameter. Mech. Based Des. Struct. Mach. 2021, 49, 738–762.
- Ghabussi, A.; Habibi, M.; NoormohammadiArani, O.; Shavalipour, A.; Moayedi, H.; Safarpour, H. Frequency characteristics of a viscoelastic graphene nanoplatelet–reinforced composite circular microplate. J. Vib. Control. 2021, 27, 101–118.
- Safarpour, M.; Ghabussi, A.; Ebrahimi, F.; Habibi, M.; Safarpour, H. Frequency characteristics of FG-GPLRC viscoelastic thick annular plate with the aid of GDQM. Thin-Walled Struct. 2020, 150, 106683.
- Habibi, M.; Darabi, R.; de Sa, J.C.; Reis, A. An innovation in finite element simulation via crystal plasticity assessment of grain morphology effect on sheet metal formability. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2021, 235, 1937–1951.
- Peng, D.; Chen, S.; Darabi, R.; Ghabussi, A.; Habibi, M. Prediction of the bending and out-of-plane loading effects on formability response of the steel sheets. Arch. Civ. Mech. Eng. 2021, 21, 1–13.
- Shariati, A.; Jung, D.W.; Mohammad-Sedighi, H.; Żur, K.K.; Habibi, M.; Safa, M. Stability and Dynamics of Viscoelastic Moving Rayleigh Beams with an Asymmetrical Distribution of Material Parameters. Symmetry 2020, 12, 586.
- Ebrahimi, F.; Hashemabadi, D.; Habibi, M.; Safarpour, H. Thermal buckling and forced vibration characteristics of a porous GNP reinforced nanocomposite cylindrical shell. Microsyst. Technol. 2020, 26, 461–473.
- Rueckes, T.; Kim, K.; Joselevich, E.; Tseng, G.Y.; Cheung, C.-L.; Lieber, C.M. Carbon nanotube-based nonvolatile random access memory for molecular computing. Science 2000, 289, 94–97.
- Wang, L.; Hu, H. Thermal vibration of a rectangular single-layered graphene sheet with quantum effects. J. Appl. Phys. 2014, 115, 233515.
- Al-Furjan, M.S.H.; Dehini, R.; Khorami, M.; Habibi, M.; Jung, D.W. On the dynamics of the ultra-fast rotating cantilever orthotropic piezoelectric nanodisk based on nonlocal strain gradient theory. Compos. Struct. 2021, 255, 112990.
- Li, S.; Chen, Z.; Wang, Y.; Huang, Y.Y.; Yu, T. Quasi-static compression and hygrothermal stability of BMI/CE co-cured composite lattice cylindrical shell. Compos. Struct. 2021, 257, 113130.
- Zhang, J.; Zhou, P.; Guan, C.; Liu, T.; Kang, W.-H.; Feng, P.; Gao, S. An ultra-lightweight CFRP beam-string structure. Compos. Struct. 2021, 257, 113149.
- Dai, Z.; Zhang, L.; Bolandi, S.Y.; Habibi, M. On the vibrations of the non-polynomial viscoelastic composite open-type shell under residual stresses. Compos. Struct. 2021, 263, 113599.
- Zhang, L.; Chen, Z.; Habibi, M.; Ghabussi, A.; Alyousef, R. Low-velocity impact, resonance, and frequency responses of FG-GPLRC viscoelastic doubly curved panel. Compos. Struct. 2021, 269, 114000.
- Brenner, D.W.; Shenderova, O.A.; Harrison, J.A.; Stuart, S.J.; Ni, B.; Sinnott, S.B. A second-generation reactive empirical bond order (REBO) potential energy expression for hydrocarbons. Mater. Sci. 2002, 14, 783–802.
- González Noya, E.; Srivastava, D.; Chernozatonskii, L.A.; Menon, M. Thermal conductivity of carbon nanotube peapods. Phys. Rev. B 2004, 70, 115416.
- Xu, Z.; Buehler, M.J. Geometry controls conformation of graphene sheets: Membranes, ribbons, and scrolls. ACS Nano 2010, 4, 3869–3876.
- Wei, N.; Fan, Z.; Xu, L.-Q.; Zheng, Y.-P.; Wang, H.-Q.; Zheng, J.-C. Knitted graphene-nanoribbon sheet: A mechanically robust structure. Nanoscale 2012, 4, 785–791.
- Chen, Y.; Zhang, Y.; Cai, K.; Jiang, J.; Zheng, J.-C.; Zhao, J.; Wei, N. Interfacial thermal conductance in graphene/black phosphorus heterogeneous structures. Carbon 2017, 117, 399–410.
- Polak, E. Optimization: Algorithms and Consistent Approximations; Springer: Berlin/Heidelberg, Germany, 1997.
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519.
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695.
- Yoon, J.; Ru, C.Q.; Mioduchowski, A. Vibration of an embedded multiwall carbon nanotube. Compos. Sci. Technol. 2003, 63, 1533–1542.
More
Information
Subjects:
Engineering, Mechanical
Contributor
MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register
:
View Times:
979
Revisions:
2 times
(View History)
Update Date:
13 Dec 2021
Notice
You are not a member of the advisory board for this topic. If you want to update advisory board member profile, please contact office@encyclopedia.pub.
OK
Confirm
Only members of the Encyclopedia advisory board for this topic are allowed to note entries. Would you like to become an advisory board member of the Encyclopedia?
Yes
No
${ textCharacter }/${ maxCharacter }
Submit
Cancel
Back
Comments
${ item }
|
More
No more~
There is no comment~
${ textCharacter }/${ maxCharacter }
Submit
Cancel
${ selectedItem.replyTextCharacter }/${ selectedItem.replyMaxCharacter }
Submit
Cancel
Confirm
Are you sure to Delete?
Yes
No




