
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Zhengzhi Mu | + 7044 word(s) | 7044 | 2021-11-03 02:37:24 | | | |
| 2 | Bruce Ren | Meta information modification | 7044 | 2021-11-04 02:35:12 | | | | |
| 3 | Lindsay Dong | Meta information modification | 7044 | 2021-11-12 09:20:58 | | |
Video Upload Options
The rise in structural performance requirements in engineering is driving the research and development of stronger, stiffer, and lighter materials. However, most traditional artificial materials are unable to meet the needs of modern industrial and technological development. In fact, multifarious creatures in nature are further ahead in their use of structural materials. There is a fairly limited selection of natural structural materials at ambient temperatures. They usually consist of hard and soft phases arranged in a complex hierarchy with characteristic dimensions ranging from nanoscale to macroscale. The resulting materials usually show a nearly perfect combination of strength and toughness integrated with lightweight characteristics. This is exactly what is required of engineering materials.
1. Introduction
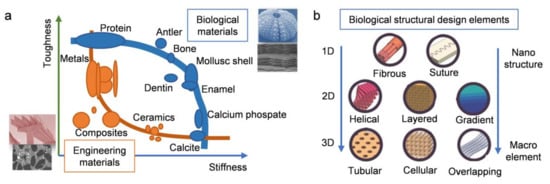
| Biological Materials | Structure Description | Highlight Mechanical Properties | Refs. | |
|---|---|---|---|---|
| 1D fibrous structures | Spider silk | Skin–core organization Fishnet-like structure |
Stiffness: the elastic modulus is 10 GPa Tensile strength: 1.1 GPa Toughness: 160 MJ m−3 |
[11][26] |
| Tendon | Uniaxial arrangement Wavy collagen fiber |
Stiffness: the elastic modulus in the range of 800–2000 MPa Tensile strength: at least 100 MPa |
[27][28] | |
| Glass sponge spicules | Hierarchical structure | Stiffness: the elastic modulus is 40.82 ± 9.65 GPa Bending strength: the fracture stress is 3727.12 ± 660.77 MPa Estimated toughness for bending: 69.45 ± 11.71 MPa |
[29] | |
| 2D layered structures | Wood | Multi-layer fiber arrangement Velcro-like recovery mechanism |
Stiffness: the modulus is 30 GPa Shear strength: 300 MPa Fracture toughness: 15–30 kJ m−2 |
[21] |
| Bone | Coaxial layered staggered structure | Stiffness: the elastic modulus is in the range of 15–20 GPa Tensile strength: 100–160 MPa Fracture toughness: 1–5 MPa m1/2 |
[7][30] | |
| Crustacean exoskeletons | Bouligand structure Fibrous pore canal tubules |
Hardness: 947 MPa Stiffness: the Young’s modulus is 1069 ± 96 MPa Toughness: 8.3 ± 1.5 MPa |
[31] | |
| Fish scales | Bouligand structure | Stiffness: the Young’s modulus is 0.86 ± 0.32 GPa Hardness: 2.0 ± 0.4 GPa Energy dissipation: 1.47 ± 1.08 MPa |
[32][33] | |
| Dactyl club of the mantis shrimp | Bouligand structure Herringbone structure |
Hardness: 65–70 GPa Compressive strength: 4GPa |
[34] | |
| Cuticle of the scorpion chela | Bouligand structure | Hardness: 230 ± 70 MPa Stiffness: the modulus is 9.5 ± 1.5 GPa |
[35] | |
| 3D cellular structures | Bird beaks | Foam structure Sandwich composite |
Low density: 0.1 g cm−3 Tensile strength: 50 MPa Stiffness: 1.4 GPa |
[36] |
| Bird bones | Dense exterior Hollow interior Reinforcing internal structures |
Flexural modulus: 6.9–7.7 Gpa Density: about 2.15 g cm−3 |
[37] | |
| Bird feather shafts | Dense exterior Hollow interior Foam structure |
Low density (foam): 0.037–0.08 g cm−3 Stiffness (cortex): 0.01–0.03 GPa |
[38] | |
| Quills | Hollow interior Foam-like core |
Buckling strength (quill): 167.9 ± 39.3 MPa Stiffness (cortex): 2.6 ± 0.7 GPa Strain energy absorbed (quill): 14.3 ± 5.9 MJ m−3 |
[39] | |
| Interface structures | Nacre | “Brick-and-mortar” architecture | Stiffness: 70–80 Gpa Tensile strength: 70–100 MPa Fracture toughness: 4–10 Mpa |
[21][40] |
| Bird feather vane | Cascade slide–lock system | Separation force: 0.72 ± 0.34 mN Self-repairing stability: separation–repair process more than 1000 times |
[41] | |
| Remora fish | Tooth-like spinules Vertical fiber structure |
Modulus (radial tension): 864 ± 334 kPa Breaking stress (circumferential tension): 2175 ± 555 kPa |
[42] | |
2. Biological Models with 1D Fibrous Structures
2.1. Spider Silk
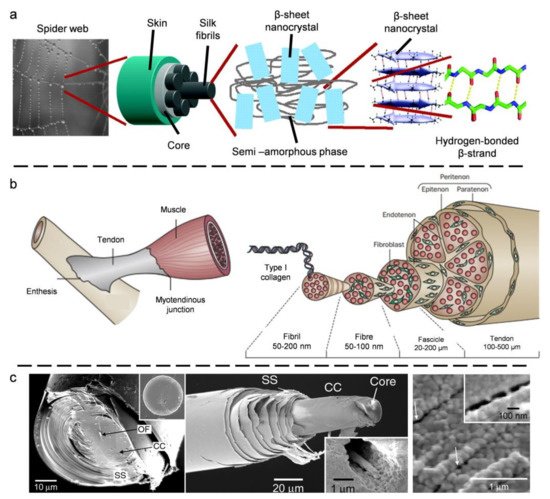
2.2. Tendon
2.3. Glass Sponge Spicules
3. Biological Models with 2D Layered Structures
3.1. Wood Tracheid
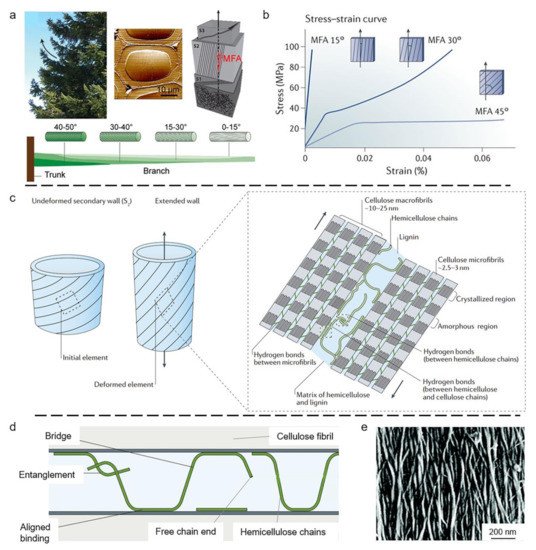
3.2. Compact Bone
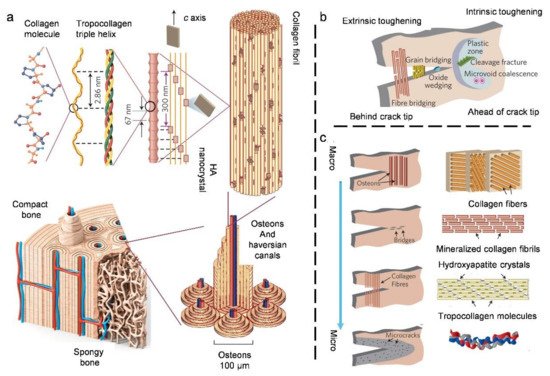
3.3. Natural Bouligand Composites
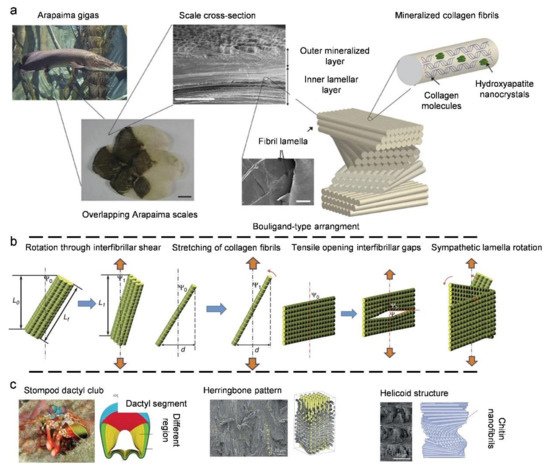
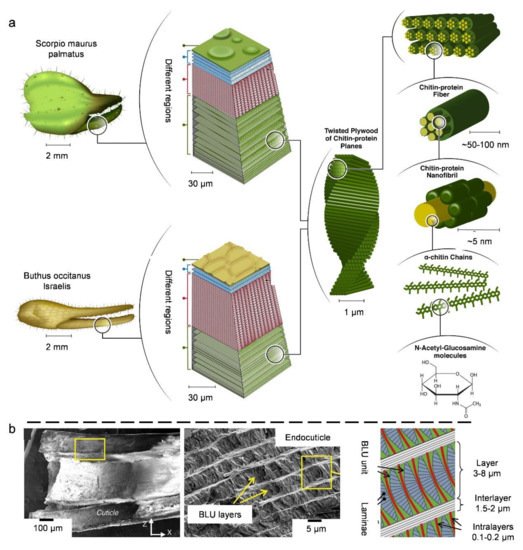
4. Biological Models with 3D Cellular Structures
4.1. Bird Beaks
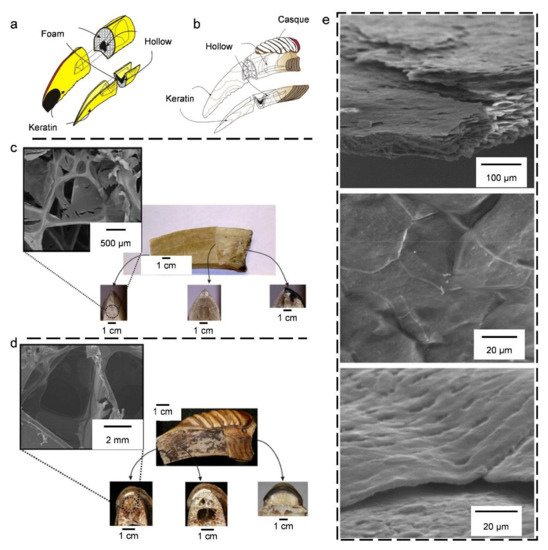
4.2. Bird Bones and Feather Shafts
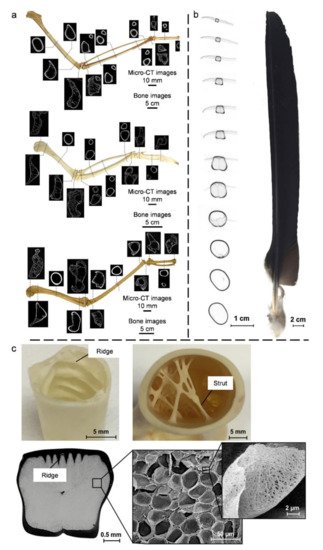
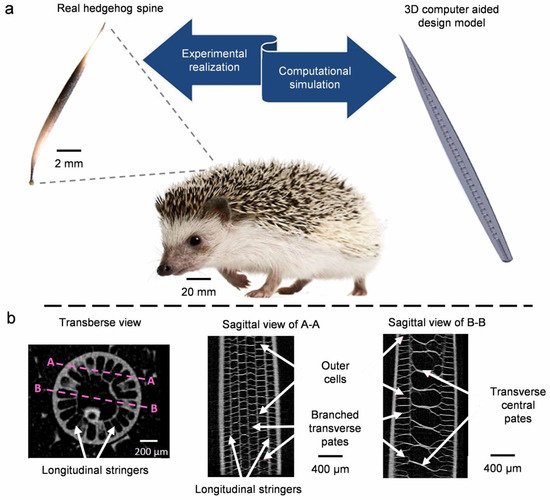
4.3. Quills
References
- Barthelat, F. Architectured materials in engineering and biology: Fabrication, structure, mechanics and performance. Int. Mater. Rev. 2016, 60, 413–430.
- Jiao, Z.B.; Chu, W.C.; Liu, L.P.; Mu, Z.Z.; Li, B.; Wang, Z.; Liao, Z.W.; Wang, Y.C.; Xue, H.; Niu, S.C.; et al. Underwater writable and heat-insulated paper with robust fluorine-free superhydrophobic coatings. Nanoscale 2020, 12, 8536–8545.
- Niu, S.C.; Li, B.; Ye, J.F.; Mu, Z.Z.; Zhang, J.Q.; Liu, Y.; Han, Z.W. Angle-dependent discoloration structures in wing scales of Morpho menelaus butterfly. Sci. China Technol. Sci. 2016, 59, 749–755.
- Han, Z.W.; Mu, Z.Z.; Li, B.; Feng, X.M.; Wang, Z.; Zhang, J.Q.; Niu, S.C.; Ren, L.Q. Bioinspired omnidirectional self-stable reflectors with multiscale hierarchical structures. ACS Appl. Mater. Interfaces. 2017, 9, 29285–29294.
- Ritchie, R.O. The conflicts between strength and toughness. Nat. Mater. 2011, 10, 817–822.
- Velasco-Hogan, A.; Xu, J.; Meyers, M.A. Additive manufacturing as a method to design and optimize bioinspired structures. Adv. Mater. 2018, 30, 1800940.
- Yaraghi, N.A.; Kisailus, D. Biomimetic structural materials: Inspiration from design and assembly. Annu. Rev. Phys. Chem. 2018, 69, 23–57.
- Wegst, U.G.; Bai, H.; Saiz, E.; Tomsia, A.P.; Ritchie, R.O. Bioinspired structural materials. Nat. Mater. 2015, 14, 23–36.
- Eder, M.; Amini, S.; Fratzl, P. Biological composites—Complex structures for functional diversity. Science 2018, 362, 543–547.
- Mao, L.B.; Gao, H.L.; Yao, H.B.; Liu, L.; Cölfen, H.; Liu, G.; Chen, S.M.; Li, S.K.; Yan, Y.X.; Liu, Y.Y. Synthetic nacre by predesigned matrix-directed mineralization. Science 2016, 354, 107–110.
- Meyers, M.A.; Chen, P.Y.; Lin, A.Y.M.; Seki, Y. Biological materials: Structure and mechanical properties. Prog. Mater. Sci. 2008, 53, 1–206.
- Chen, P.Y.; McKittrick, J.; Meyers, M.A. Biological materials: Functional adaptations and bioinspired designs. Prog. Mater. Sci. 2012, 57, 1492–1704.
- Wang, B.; Yang, W.; McKittrick, J.; Meyers, M.A. Keratin: Structure, mechanical properties, occurrence in biological organisms, and efforts at bioinspiration. Prog. Mater. Sci. 2016, 76, 229–318.
- Liu, Z.; Meyers, M.A.; Zhang, Z.; Ritchie, R.O. Functional gradients and heterogeneities in biological materials: Design principles, functions, and bioinspired applications. Prog. Mater. Sci. 2017, 88, 467–498.
- Yang, W.; Meyers, M.A.; Ritchie, R.O. Structural architectures with toughening mechanisms in Nature: A review of the materials science of Type-I collagenous materials. Prog. Mater. Sci. 2019, 103, 425–483.
- Naleway, S.E.; Porter, M.M.; McKittrick, J.; Meyers, M.A. Structural design elements in biological materials: Application to bioinspiration. Adv. Mater. 2015, 27, 5455–5476.
- Wang, J.; Cheng, Q.; Tang, Z. Layered nanocomposites inspired by the structure and mechanical properties of nacre. Chem. Soc. Rev. 2012, 41, 1600360.
- Frezzo, J.A.; Montclare, J.K. Natural composite systems for bioinspired materials. Adv. Exp. Med. Biol. 2016, 940, 143–166.
- Natarajan, B.; Gilman, J.W. Bioinspired Bouligand cellulose nanocrystal composites: A review of mechanical properties. Philos. Trans. R. Soc. A-Math. Phys. Eng. Sci. 2018, 376, 20170050.
- Zhao, H.; Yang, Z.; Guo, L. Nacre-inspired composites with different macroscopic dimensions: Strategies for improved mechanical performance and applications. NPG Asia Mater. 2018, 10, 1–22.
- Barthelat, F.; Yin, Z.; Buehler, M.J. Structure and mechanics of interfaces in biological materials. Nat. Rev. Mater. 2016, 1, 16007.
- Ren, J.; Wang, Y.; Yao, Y.; Wang, Y.; Fei, X.; Qi, P.; Lin, S.; Kaplan, D.L.; Buehler, M.J.; Ling, S. Biological material interfaces as inspiration for mechanical and optical material designs. Chem. Rev. 2019, 119, 12279–12336.
- Prabhakaran, R.T.D.; Spear, M.J.; Curling, S.; Wootton-Beard, P.; Jones, P.; Donnison, I.; Ormondroyd, G.A. Plants and architecture: The role of biology and biomimetics in materials development for buildings. Intell. Build. Int. 2019, 11, 178–211.
- Zhang, B.; Han, Q.; Zhang, J.; Han, Z.; Niu, S.; Ren, L. Advanced bio-inspired structural materials: Local properties determine overall performance. Mater. Today 2020, 41, 177–199.
- Mallick, P.K. Fiber-Reinforced Composites: Materials, Manufacturing, and Design; CRC Press: Boca Raton, FL, USA, 2007.
- Guan, Q.F.; Han, Z.M.; Zhu, Y.; Xu, W.L.; Yang, H.B.; Ling, Z.C.; Yan, B.; Yang, K.; Yin, C.; Wu, H.; et al. Bio-inspired lotus-fiber-like spiral hydrogel bacterial cellulose fibers. Nano Lett. 2021, 21, 952–958.
- Blackledge, T.A.; Hayashi, C.Y. Silken toolkits: Biomechanics of silk fibers spun by the orb web spider Argiope argentata (Fabricius 1775). J. Exp. Biol. 2006, 209, 2452–2461.
- Vehoff, T.; Glišović, A.; Schollmeyer, H.; Zippelius, A.; Salditt, T. Mechanical properties of spider dragline silk: Humidity, hysteresis, and relaxation. Biophys. J. 2007, 93, 4425–4432.
- Zlotnikov, I.; Masic, A.; Dauphin, Y.; Fratzl, P.; Zolotoyabko, E. Composition and mechanical properties of a protein/silica hybrid material forming the micron-thick axial filament in the spicules of marine sponges. Adv. Eng. Mater. 2014, 16, 1073–1077.
- Sinko, R.; Qin, X.; Keten, S. Interfacial mechanics of cellulose nanocrystals. MRS Bull. 2015, 40, 340–348.
- Thuvander, F.; Berglund, L.A. In situ observations of fracture mechanisms for radial cracks in wood. J. Mater. Sci. 2000, 35, 6277–6283.
- Launey, M.E.; Buehler, M.J.; Ritchie, R.O. On the mechanistic origins of toughness in bone. Ann. Rev. Mater. Res. 2010, 40, 25–53.
- Gupta, H.S.; Wagermaier, W.; Zickler, G.A.; Raz-Ben Aroush, D.; Funari, S.S.; Roschger, P.; Wagner, H.D.; Fratzl, P. Nanoscale deformation mechanisms in bone. Nano Lett. 2005, 5, 2108–2111.
- Fantner, G.E.; Hassenkam, T.; Kindt, J.H.; Weaver, J.C.; Birkedal, H.; Pechenik, L.; Cutroni, J.A.; Cidade, G.A.; Stucky, G.D.; Morse, D.E. Sacrificial bonds and hidden length dissipate energy as mineralized fibrils separate during bone fracture. Nat. Mater. 2005, 4, 612–616.
- Sachs, C.; Fabritius, H.; R-Aabe, D. Influence of microstructure on deformation anisotropy of mineralized cuticle from the lobster Homarus americanus. J. Struct. Biol. 2008, 161, 120–132.
- Lin, Y.; Wei, C.; Olevsky, E.; Meyers, M.A. Mechanical properties and the laminate structure of Arapaima gigas scales. J. Mech. Behav. Biomed. Mater. 2011, 4, 1145–1156.
- Patek, S.N.; Korff, W.; Caldwell, R.L. Biomechanics: Deadly strike mechanism of a mantis shrimp—This shrimp packs a punch powerful enough to smash its prey’s shell underwater. Nature 2004, 428, 819–820.
- Yaraghi, N.A.; Guarín-Zapata, N.; Grunenfelder, L.K.; Hintsala, E.; Bhowmick, S.; Hiller, J.M.; Betts, M.; Principe, E.L.; Jung, J.Y.; Sheppard, L. A sinusoidally architected helicoidal biocomposite. Adv. Mater. 2016, 28, 6835–6844.
- Seki, Y.; Schneider, M.S.; Meyers, M.A. Structure and mechanical behavior of a toucan beak. Acta Mater. 2005, 53, 5281–5296.
- De Margerie, E. Laminar bone as an adaptation to torsional loads in flapping flight. J. Anat. 2002, 201, 521–526.
- Drol, C.J.; Kennedy, E.B.; Hsiung, B.K.; Swift, N.B.; Tan, K.T. Bioinspirational understanding of flexural performance in hedgehog spines. Acta Biomater. 2019, 94, 553–564.
- Xi, S.; Tian, F.; Wei, G.; He, X.; Shang, Y.; Ju, Y.; Li, W.; Lu, Q.; Wang, Q. Reversible dendritic-crystal-reinforced polymer gel for bioinspired adaptable adhesive. Adv. Mater. 2021, 33, 2103174.
- Xu, X.; Li, L.; Seraji, S.M.; Liu, L.; Jiang, Z.; Xu, Z.; Li, X.; Zhao, S.; Wang, H.; Song, P. Bioinspired, strong, and tough nanostructured poly(vinyl alcohol)/inositol composites: How hydrogen-bond cross-linking works? Macromolecules 2021, 1c01725.
- Kono, N.; Nakamura, H.; Mori, M.; Yoshida, Y.; Ohtoshi, R.; Malay, A.D.; Moran, D.A.P.; Tomita, M.; Numata, K.; Arakawa, K. Multicomponent nature underlies the extraordinary mechanical properties of spider dragline silk. Proc. Natl. Acad. Sci. USA 2021, 3, e2107065118.
- Zan, G.; Wu, T.; Zhu, F.; He, P.; Cheng, Y.; Chai, S.; Wang, Y.; Huang, X.; Zhang, W.; Wan, Y.; et al. A biomimetic conductive super-foldable material. Matter 2021, 4, 3232–3247.
- Liu, C.; Li, B.; Li, Z.; Cao, C.; Gao, X.; Zhang, K.; Chen, H. 3D printable and fringe electric field adhesion enabled variable stiffness artificial muscles for semi-active vibration attenuation. Soft Matter 2021, 17, 6678–6902.
- Ling, S.J.; Kaplan, D.L.; Buehler, M.J. Nanofibrils in nature and materials engineering. Nat. Rev. Mater. 2018, 3, 18016.
- Nova, A.; Keten, S.; Pugno, N.M.; Redaelli, A.; Buehler, M.J. Molecular and nanostructural mechanisms of deformation, strength and toughness of spider silk fibrils. Nano Lett. 2010, 10, 2626–2634.
- Heim, M.; Römer, L.; Scheibel, T. Hierarchical structures made of proteins. The complex architecture of spider webs and their constituent silk proteins. Chem. Soc. Rev. 2010, 39, 156–164.
- Foelix, R. Biology of Spiders; OUP: Cary, NC, USA, 2011.
- Keten, S.; Xu, Z.; Ihle, B.; Buehler, M.J. Nanoconfinement controls stiffness, strength and mechanical toughness of β-sheet crystals in silk. Nat. Mater. 2010, 9, 359–367.
- Sinan, K.; Buehler, M.J. Nanostructure and molecular mechanics of spider dragline silk protein assemblies. J. R. Soc. Interface 2010, 7, 1709–1721.
- Asakura, T.; Suzuki, Y.; Nakazawa, Y.; Holland, G.P.; Yarger, J.L. Elucidating silk structure using solid-state NMR. Soft Matter 2013, 9, 11440–11450.
- Liu, R.; Deng, Q.; Yang, Z.; Yang, D.; Han, M.Y.; Liu, X.Y. “Nano-fishnet” structure making silk fibers tougher. Adv. Funct. Mater. 2016, 26, 5534–5541.
- Geoffroy, N.; Francis, B.; Delphine, D. Tendon injury: From biology to tendon repair. Nat. Rev. Rheumatol. 2015, 11, 223–233.
- Aizenberg, J.; Sundar, V.C.; Yablon, A.D.; Weaver, J.C.; Chen, G. Biological glass fibers: Correlation between optical and structural properties. Proc. Natl. Acad. Sci. USA 2004, 101, 3358–3363.
- Lipman, K.; Wang, C.; Ting, K.; Soo, C.; Zheng, Z. Tendinopathy: Injury, repair, and current exploration. Drug. Des. Devel. Ther. 2018, 12, 591–603.
- Watanabe, T.; Imamura, Y.; Hosaka, Y.; Ueda, H.; Takehana, K. Graded arrangement of collagen fibrils in the equine superficial digital flexor tendon. Connect. Tissue Res. 2007, 48, 332–337.
- Screen, H.; Bader, D.; Lee, D.; Shelton, J.J.S. Local strain measurement within tendon. Strain 2004, 40, 157–163.
- Ker, R.F. Mechanics of tendon, from an engineering perspective. Strain 2007, 29, 1001–1009.
- Müller, W.E.; Krasko, A.; Le Pennec, G.; Schröder, H.C. Biochemistry and cell biology of silica formation in sponges. Microsc. Res. Tech. 2003, 62, 368–377.
- Mayer, G. Mechanical energy dissipation in natural ceramic composites. J. Mech. Behav. Biomed. Mater. 2017, 76, 21–29.
- Drozdov, A.L.; Andreykin, N.A.; Dorofeev, A.G. Structure and physico-chemical properties of organosilicon crystal-like composite spicules of the glass sponge Hyalonema sieboldi. Mater. Res. Bull. 2018, 105, 372–376.
- Aizenberg, J.; Weaver, J.C.; Thanawala, M.S.; Sundar, V.C.; Morse, D.E.; Fratzl, P. Skeleton of Euplectella sp.: Structural hierarchy from the nanoscale to the macroscale. Science 2005, 309, 275–278.
- Cha, J.N.; Stucky, G.D.; Morse, D.E.; Deming, T.J. Biomimetic synthesis of ordered silica structures mediated by block copolypeptides. Nature 2000, 403, 289–292.
- Walter, S.L.; Flinn, B.D.; Mayer, G. Mechanisms of toughening of a natural rigid composite. Mater. Sci. Eng. C-Mater. Biol. Appl. 2007, 27, 570–574.
- Miserez, A.; Weaver, J.C.; Thurner, P.J.; Aizenberg, J.; Dauphin, Y.; Fratzl, P.; Morse, D.E.; Zok, F.W. Effects of laminate architecture on fracture resistance of sponge biosilica: Lessons from nature. Adv. Funct. Mater. 2008, 18, 1241–1248.
- Feng, Y.; Gao, H.L.; Wu, D.; Weng, Y.T.; Wang, Z.Y.; Yu, S.H.; Wang, Z. Biomimetic lamellar chitosan scaffold for soft gingival tissue regeneration. Adv. Funct. Mater. 2021, 31, 2105348.
- Han, Q.; Shi, S.; Liu, Z.; Han, Z.; Niu, S.; Zhang, J.; Qin, H.; Sun, Y.; Wang, J. Study on impact resistance behaviors of a novel composite laminate with basalt fiber for helical-sinusoidal bionic structure of dactyl club of mantis shrimp. Compos. Part B Eng. 2020, 191, 107976.
- Mohammadi, P.; Gandier, J.A.; Nonappa, N.; Wagermaier, W.; Miserez, A.; Penttilä, M. Bioinspired functionally graded composite assembled using cellulose nanocrystals and genetically engineered proteins with controlled biomineralization. Adv. Mater. 2021, 33, 2102658.
- Yin, S.; Yang, R.; Huang, Y.; Guo, W.; Chen, D.; Zhang, W.; Ren, M.; Zhou, Y.; Xu, J. Toughening mechanism of coelacanth-fish-inspired double-helicoidal composites. Compos. Sci. Technol. 2021, 205, 108650.
- Wang, Y.; Liao, W.; Sun, J.; Nandi, R.; Yang, Z. Bioinspired construction of artificial cardiac muscles based on liquid crystal elastomer fibers. Adv. Mater. Technol. 2021. online, 2100934.80.
- Lichtenegger, H.; Reiterer, A.; Stanzl-Tschegg, S.; Fratzl, P. Variation of cellulose microfibril angles in softwoods and hardwoods—A possible strategy of mechanical optimization. J. Struct. Biol. 1999, 128, 257–269.
- Xing, Y.; Jones, P.; Bosch, M.; Donnison, I.; Spear, M.; Ormondroyd, G. Exploring design principles of biological and living building envelopes: What can we learn from plant cell walls? Intell. Build. Int. 2018, 10, 78–102.
- Fratzl, P.; Burgert, I.; Keckes, J. Mechanical model for the deformation of the wood cell wall. Z. Metallk. 2004, 95, 579–584.
- Keckes, J.; Burgert, I.; Frühmann, K.; Müller, M.; Kölln, K.; Hamilton, M.; Burghammer, M.; Roth, S.V.; Stanzl-Tschegg, S.; Fratzl, P. Cell-wall recovery after irreversible deformation of wood. Nat. Mater. 2003, 2, 810–813.
- Spatz, H.; Kohler, L.; Niklas, K.J. Mechanical behaviour of plant tissues: Composite materials or structures? J. Exp. Biol. 1999, 202, 3269–3272.
- Altaner, C.; Jarvis, M.J. Modelling polymer interactions of the ‘molecular Velcro’ type in wood under mechanical stress. J. Theor. Biol. 2008, 253, 434–445.
- Ng, T.P.; Koloor, S.S.R.; Djuansjah, J.R.P.; Kadir, M.A. Assessment of compressive failure process of cortical bone materials using damage-based model. J. Mech. Behav. Biomed. Mater. 2017, 66, 1–11.
- Hambli, R. Micro-CT finite element model and experimental validation of trabecular bone damage and fracture. Bone 2013, 56, 363–374.
- Peng, J.; Cheng, Q. High-Performance Nanocomposites Inspired by Nature. Adv Mater. 2017, 29, 1702959.
- Blob, R.W.; Snelgrove, J.M.J.J.o.M. Antler stiffness in moose (Alces alces): Correlated evolution of bone function and material properties? J. Morphol. 2006, 267, 1075–1086.
- Tai, K.; Ulm, F.-J.; Ortiz, C. Nanogranular origins of the strength of bone. Nano Lett. 2006, 6, 2520–2525.
- Skedros, J.G.; Holmes, J.L.; Vajda, E.G.; Bloebaum, R.D. Cement lines of secondary osteons in human bone are not mineral-deficient: New data in a historical perspective. Anat. Rec. Part A Discov. Mol. Cell. Evol. Biol. Off. Publ. Am. Assoc. Anat. 2005, 286, 781–803.
- Bouligand, Y. Twisted fibrous arrangements in biological materials and cholesteric mesophases. Tissue Cell. 1972, 4, 189–217.
- Chen, P.Y.; Lin, A.Y.M.; McKittrick, J.; Meyers, M.A. Structure and mechanical properties of crab exoskeletons. Acta Biomater. 2008, 4, 587–596.
- Kunkel, J.G.; Nagel, W.; Jercinovic, M.J. Mineral fine structure of the American lobster cuticle. J. Shellfish Res. 2012, 31, 515–526.
- Nikolov, S.; Petrov, M.; Lymperakis, L.; Friák, M.; Sachs, C.; Fabritius, H.O.; Raabe, D.; Neugebauer, J. Revealing the design principles of high-performance biological composites using ab initio and multiscale simulations: The example of lobster cuticle. Adv. Mater. 2010, 22, 519–526.
- Zimmermann, E.A.; Gludovatz, B.; Schaible, E.; Dave, N.K.; Yang, W.; Meyers, M.A.; Ritchie, R.O. Mechanical adaptability of the Bouligand-type structure in natural dermal armour. Nat. Commun. 2013, 4, 1–7.
- Yang, W.; Sherman, V.R.; Gludovatz, B.; Mackey, M.; Zimmermann, E.A.; Chang, E.H.; Schaible, E.; Qin, Z.; Buehler, M.J.; Ritchie, R.O. Protective role of Arapaima gigas fish scales: Structure and mechanical behavior. Acta Biomater. 2014, 10, 3599–3614.
- Weaver, J.C.; Milliron, G.W.; Miserez, A.; Evans-Lutterodt, K.; Herrera, S.; Gallana, I.; Mershon, W.J.; Swanson, B.; Zavattieri, P.; DiMasi, E. The stomatopod dactyl club: A formidable damage-tolerant biological hammer. Science 2012, 336, 1275–1280.
- Patek, S.; Caldwell, R.L. Extreme impact and cavitation forces of a biological hammer: Strike forces of the peacock mantis shrimp Odontodactylus scyllarus. J. Exp. Biol. 2005, 208, 3655–3664.
- Amini, S.; Tadayon, M.; Idapalapati, S.; Miserez, A. The role of quasi-plasticity in the extreme contact damage tolerance of the stomatopod dactyl club. Nat. Mater. 2015, 14, 943–950.
- Kellersztein, I.; Cohen, S.R.; Bar-On, B.; Wagner, H.D. The exoskeleton of scorpions’ pincers: Structure and micro-mechanical properties. Acta Biomater. 2019, 94, 565–573.
- Greenfeld, I.; Kellersztein, I.; Wagner, H.D. Nested helicoids in biological microstructures. Nat. Commun. 2020, 11, 1–12.
- Meng, L.; Lan, X.; Zhao, J.; Hao, L.; Zemin, W.; Liang, G. Failure analysis of bio-inspired corrugated sandwich structures fabricated by laser powder bed fusion under three-point bending. Compos. Struct. 2021, 263, 113724.
- Xu, J.; Liu, T.; Zhang, Y.; Zhang, Y.; Wu, K.; Lei, C.; Qiang, F.; Fu, J. Dragonfly wing-inspired architecture makes a stiff yet tough healable material. Matter 2021, 4, 2474–2489.
- Seki, Y.; Kad, B.; Benson, D.; Meyers, M.A. The toucan beak: Structure and mechanical response. Mater. Sci. Eng. C-Mater. Biol. Appl. 2006, 26, 1412–1420.
- Seki, Y.; Bodde, S.G.; Meyers, M.A. Toucan and hornbill beaks: A comparative study. Acta Biomater. 2010, 6, 331–343.
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties; Cambridge University Press: Cambridge, UK, 1997.
- Meyers, M.A.; Lin, A.Y.; Seki, Y.; Chen, P.-Y.; Kad, B.K.; Bodde, S. Structural biological composites: An overview. JOM 2006, 58, 35–41.
- Cubo, J.; Casinos, A. Incidence and mechanical significance of pneumatization in the long bones of birds. Zool. J. Linn. Soc. 2000, 130, 499–510.
- Sullivan, T.N.; Wang, B.; Espinosa, H.D.; Meyers, M.A. Extreme lightweight structures: Avian feathers and bones. Mater. Today 2017, 20, 377–391.
- Dumont, E.R. Bone density and the lightweight skeletons of birds. Proc. R. Soc. B-Biol. Sci. 2010, 277, 2193–2198.
- Wang, B.; Sullivan, T.N. A review of terrestrial, aerial and aquatic keratins: The structure and mechanical properties of pangolin scales, feather shafts and baleen plates. J. Mech. Behav. Biomed. Mater. 2017, 76, 4–20.
- Wang, B.; Meyers, M.A. Light like a feather: A fibrous natural composite with a shape changing from round to square. Adv. Sci. 2017, 4, 1600360.
- Laurent, C.M.; Palmer, C.; Boardman, R.P.; Dyke, G.; Cook, R.B. Nanomechanical properties of bird feather rachises: Exploring naturally occurring fibre reinforced laminar composites. J. R. Soc. Interface. 2014, 11, 20140961.
- Wang, B.; Meyers, M.A. Seagull feather shaft: Correlation between structure and mechanical response. Acta Biomater. 2017, 48, 270–288.
- Vincent, J.F.; Owers, P. Mechanical design of hedgehog spines and porcupine quills. J. Zool. 1986, 210, 55–75.
- Karam, G.; Gibson, L.J. Biomimicking of animal quills and plant stems: Natural cylindrical shells with foam cores. Mater. Sci. Eng. C-Mater. Biol. Appl. 1994, 2, 113–132.
- Yang, W.; McKittrick, J. Separating the influence of the cortex and foam on the mechanical properties of porcupine quills. Acta Biomater. 2013, 9, 9065–9074.
- Busson, B.; Engström, P.; Doucet, J. Existence of various structural zones in keratinous tissues revealed by X-ray microdiffraction. J. Synchrot. Radiat. 1999, 6, 1021–1030.
- Chou, S.F.; Overfelt, R.A. Tensile deformation and failure of North American porcupine quills. Mater. Sci. Eng. C-Mater. Biol. Appl. 2011, 31, 1729–1736.
- Torres, F.G.; Troncoso, O.P.; Diaz, J.; Arce, D. Failure analysis of porcupine quills under axial compression reveals their mechanical response during buckling. J. Mech. Behav. Biomed. Mater. 2014, 39, 111–118.
- Swift, N.B.; Hsiung, B.K.; Kennedy, E.B.; Tan, K.T. Dynamic impact testing of hedgehog spines using a dual-arm crash pendulum. J. Mech. Behav. Biomed. Mater. 2016, 61, 271–282.




