Properties of Multi-Dimensional Biological Models with Cross-Scale Features: Comparison
View Latest Version
Please note this is a comparison between Version 3 by Lindsay Dong and Version 2 by Bruce Ren.

The rise in structural performance requirements in engineering is driving the research and development of stronger, stiffer, and lighter materials. However, most traditional artificial materials are unable to meet the needs of modern industrial and technological development. In fact, multifarious creatures in nature are further ahead in their use of structural materials. There is a fairly limited selection of natural structural materials at ambient temperatures. They usually consist of hard and soft phases arranged in a complex hierarchy with characteristic dimensions ranging from nanoscale to macroscale. The resulting materials usually show a nearly perfect combination of strength and toughness integrated with lightweight characteristics. This is exactly what is required of engineering materials.

  • biomimetic composites
  • hierarchical structures
  • structural elements
  • biological models
  • mechanical properties

1. Introduction

The requirements for material performance in modern engineering applications are getting higher and higher, and materials are also required to possess stronger, tougher, lighter and more versatile properties [1][2][3][4]. For engineering materials, certain seemingly contradictory properties (e.g., strength and toughness) are perfectly reflected in biological materials [5]. Figure 1a illustrates the relationship between the fracture resistance and elastic deformation resistance of different materials [6]. In general, for engineering materials, an increase in elastic modulus is often accompanied by a decrease in toughness, while the stiffness of biological materials can be significantly increased without reducing the toughness. Such materials may benefit from the advantages of long-term evolution in nature. In fact, after millions of years of brutal selective evolution, many natural structural materials in creatures are made of relatively inferior components, such as fragile inorganic minerals (calcium carbonate, calcium phosphate, silicon dioxide, etc.) and soft natural polymer (proteins, polysaccharides, etc.). However, with the help of their multi-level ordered structures and complex interface layouts, these materials can have unique mechanical properties that maintain basic life activities [7][8][9]. The unique structure–property relationship of natural materials strongly proves that the influence of structure on material properties cannot be ignored [8][10].
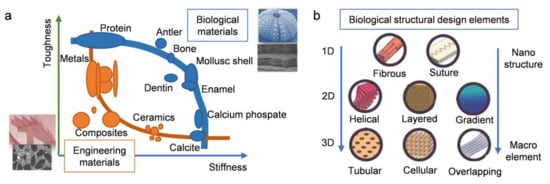
Coatings 11 01297 g001 550
Figure 1. (a) Toughness and stiffness for different materials. (b) Diagram of the eight most common biological structural design elements. Reprinted with permission from [6], copyright 2018 WILEY-V C H VERLAG GMBH.
Since 2008, massive amounts of progress regarding research on biological materials from different perspectives has been reported. Meyers [11] summarized the basic building blocks of biological materials and introduced the principal mechanical characteristics and structures in detail according to the classification of Wegst and Ashby. Chen et al. [12] reviewed the biological materials for their primary functional purpose, which include impact or fracture resistance, armor and protection, sharp and cutting components, lightweight properties for flight or special nanomechanical/chemical extremities for reversible adhesive purposes. Wegst et al. [8] reviewed the common design motifs of some typical natural structural materials and discussed the difficulties associated with the design and fabrication of synthetic structures. Wang et al. [13] focused on the structural features and mechanical properties of proteins that make up biological materials. Liu et al. [14] reviewed the basic design forms and principles of naturally occurring gradients in biological materials and discussed the functions and benefits that they confer to organisms. Yang et al. [15] reviewed the structure, deformation and toughening mechanisms of collagen materials from the perspective of the assembly of collagen molecules, fibrils, fibers, and hierarchical elements. Naleway et al. [16] summarized the eight elements of biological structural design (Figure 1b) and described their basic mechanical and/or structural advantages. As a typical biological structural material, nacre and arthropod cuticles have been extensively investigated. Great achievements have also been made in the field of biomimetic fabrication, using them as biological templates [7][17][18][19][20]. As an important influencing factor on the mechanics of biological materials, interfaces of biological materials were well discussed by Barthelat [21]. It showed that these interfaces possess unusual mechanical characteristics. Ren et al. [22] particularly focused on the biological material interfaces and interface-inspired materials from mechanical and optical perspectives. Moreover, the architecture and building elements inspired by biological materials were also reviewed [1][23]. Recently, Zhang et al. [24] reviewed how natural materials optimize overall performance by adjusting local properties.
Most of the above-mentioned research mainly focused on preparation methods of biomimetic structures in artificial materials, the mechanism of the relationship between structure and performance and their applications in specific fields. It should be noted that due to the complexity and compositional diversity of biological materials, the structure of the same organism may be divided into distinct groups by different classification methods. Taking the nacre structure with excellent mechanical properties as an example, it can be divided into biological ceramics according to its main material composition [11]. On the other hand, it can also be divided into layered structures according to the arrangement of its calcium carbonate platelets [16]. Due to the complex and efficient interface, it has been taken as an example of interface materials [22]. Many engineering materials usually present multiple dimensions. Taking fiber-reinforced composites as an example, the fibers used as the reinforcing phase have a one-dimensional (1D) structure, while the fiber cloth used for layup has a two-dimensional (2D) structure. The final composite material is usually a three-dimensional (3D) structure. In addition, an interface is formed between fibers and matrix [25]. Structural materials of different dimensions abound in nature. Learning from the abundant structures of typical biological materials is the key to understanding the superiority of bionic strategies in manufacturing new artificial synthetic materials.
In this review, we divided different biological materials into the following types of structural elements based on their dimensions: 1D fibrous structures, 2D layered structures, 3D cellular structures and heterogeneous interface structures. To adapt to extremely harsh living environments, creatures in nature have evolved multi-dimensional structures that exhibit excellent mechanical properties (Table 1). The mechanism of the relationship between structure and performance was explained in detail. Finally, a critical outlook of the development of next-generation materials with excellent mechanical properties by synthesizing bionic strategies of different dimensions and different creatures was provided, which will better satisfy the demand for the research development of engineering and industrial materials.
Table 1. Multi-dimensional structures of typical biological models in nature.
Biological Materials Structure Description Highlight Mechanical Properties Refs.
1D fibrous structures Spider silk Skin–core organization

Fishnet-like structure		 Stiffness: the elastic modulus is 10 GPa

Tensile strength: 1.1 GPa

Toughness: 160 MJ m−3		 [11][26]
Tendon Uniaxial arrangement

Wavy collagen fiber		 Stiffness: the elastic modulus in the range of 800–2000 MPa

Tensile strength: at least 100 MPa		 [27][28]
Glass sponge spicules Hierarchical structure Stiffness: the elastic modulus is 40.82 ± 9.65 GPa

Bending strength: the fracture stress is 3727.12 ± 660.77 MPa

Estimated toughness for bending: 69.45 ± 11.71 MPa		 [29]
2D layered structures Wood Multi-layer fiber arrangement

Velcro-like recovery mechanism		 Stiffness: the modulus is 30 GPa

Shear strength: 300 MPa

Fracture toughness: 15–30 kJ m−2		 [21]
Bone Coaxial layered staggered structure Stiffness: the elastic modulus is in the range of 15–20 GPa

Tensile strength: 100–160 MPa

Fracture toughness: 1–5 MPa m1/2		 [7][30]
Crustacean exoskeletons Bouligand structure

Fibrous pore canal tubules		 Hardness: 947 MPa

Stiffness: the Young’s modulus is 1069 ± 96 MPa

Toughness: 8.3 ± 1.5 MPa		 [31]
Fish scales Bouligand structure Stiffness: the Young’s modulus is 0.86 ± 0.32 GPa

Hardness: 2.0 ± 0.4 GPa

Energy dissipation: 1.47 ± 1.08 MPa		 [32][33]
Dactyl club of the mantis shrimp Bouligand structure

Herringbone structure		 Hardness: 65–70 GPa

Compressive strength: 4GPa		 [34]
Cuticle of the scorpion chela Bouligand structure Hardness: 230 ± 70 MPa

Stiffness: the modulus is 9.5 ± 1.5 GPa		 [35]
3D cellular structures Bird beaks Foam structure

Sandwich composite		 Low density: 0.1 g cm−3

Tensile strength: 50 MPa

Stiffness: 1.4 GPa		 [36]
Bird bones Dense exterior

Hollow interior

Reinforcing internal structures		 Flexural modulus: 6.9–7.7 Gpa

Density: about 2.15 g cm−3		 [37]
Bird feather shafts Dense exterior

Hollow interior

Foam structure		 Low density (foam): 0.037–0.08 g cm−3

Stiffness (cortex): 0.01–0.03 GPa		 [38]
Quills Hollow interior

Foam-like core		 Buckling strength (quill): 167.9 ± 39.3 MPa

Stiffness (cortex): 2.6 ± 0.7 GPa

Strain energy absorbed (quill): 14.3 ± 5.9 MJ m−3		 [39]
Interface structures Nacre “Brick-and-mortar” architecture Stiffness: 70–80 Gpa

Tensile strength: 70–100 MPa

Fracture toughness: 4–10 Mpa		 [21][40]
Bird feather vane Cascade slide–lock system Separation force: 0.72 ± 0.34 mN

Self-repairing stability: separation–repair process more than 1000 times		 [41]
Remora fish Tooth-like spinules

Vertical fiber structure		 Modulus (radial tension): 864 ± 334 kPa

Breaking stress (circumferential tension): 2175 ± 555 kPa		 [42]

2. Biological Models with 1D Fibrous Structures

One-dimensional fibrous structures can be found in a variety of biological materials. Spider silk and natural silk usually have extremely high tensile strength and high elasticity [43][44][45], while muscle fibers have excellent fatigue resistance [46]. The lotus silk fiber in the lotus leaf provides the lotus root and petiole with excellent resistance to breakage and is used in the design of surgical sutures [26]. Another biological sponge that lives in water has excellent toughness. They are commonly found within non-mineralized, soft biological materials, such as muscle, tendon and silks. However, there are many notable exceptions, such as the glass sponge and the chitin fibers in arthropod exoskeletons, where these fibers are mineralized. They usually share some common characteristics such as confined fibrillary dimensions, hierarchical architecture, as well as interface interactions [11][47]. These fibrous structures strengthen and toughen materials by limiting fiber shear and controlling slip, stress transfer and energy dissipation [11][48][49]. Specific examples given here are spider silk, tendon and glass sponge.

2.1. Spider Silk

Spiders usually use different silks to achieve a variety of tasks. Spider silk is famous for its incredible toughness. Due to its fascinating mechanical properties, spider silk has attracted researchers’ attention for a long time, especially in the field of biomaterial science. Spiders can produce more than seven different types of spider silks through different glands. These glands can be distinguished morphologically and histologically as ampullate glands, piriform glands, aciniform glands, tubuliform glands, aggregate glands and flagelliform glands. Spider silk secreted by different silk glands has different physical properties that achieve different functions and build complex spider webs [50]. Dragline silk, also called major ampullate silk, is the strongest fiber, and aciniform silk is known for its extreme toughness [27]. These two silks are also the most studied. Dragline silk acts as a supporting or safety silk, which constitutes the spokes and frames of the cobweb and the hanging lines for the spider. Its elastic modulus is about 10 GPa and its maximum strength exceeds 1 GPa [28]. On the other hand, aciniform silk can withstand up to 500% strain before failure in some species. However, they both have surprisingly similar and incredible toughness [11][51].
Dragline silk has natural hierarchical structures (Figure 2a) [52]. Dragline silk fiber has a skin–core organization, with a multitude of fibrillar substructures and covered by hard skin [52]. Silk fibril can be thought of as a semi-crystalline material which has a fishnet-like structure composed of interconnected β-sheet nanocrystals and amorphous proteins [11][53]. The β-sheet nanocrystals serve as nodes carrying stress in a fishnet-like structure, while amorphous proteins connect nodes (β-sheet nanocrystals) like a rope to form a structure that is both flexible and strong [54]. Further, these nanocrystals are formed by layers of anti-parallel amino acid sequences, which are called β-pleated sheets [11][51]. These β-sheet nanocrystals, only a few nanometers in size, account for about 10–15% of the volume of silk, which are bonded with hydrogen bonds. The hierarchical structure also includes the electron density at the angstrom scale [51]. When silk fibers are exposed to stretch, β-sheet nanocrystals form interlocking regions that are used to transfer loads between partially stretched and oriented macromolecular chains. Due to the contribution of hydrogen bonding, the cohesion provided by the β-sheet nanocrystals between the long polypeptide chains enables the amorphous domains to stretch significantly. Eventually, the β-sheet nanocrystals fracture under large deformation and loads, where the typical loading at individual β-sheet nanocrystals is lateral [51].
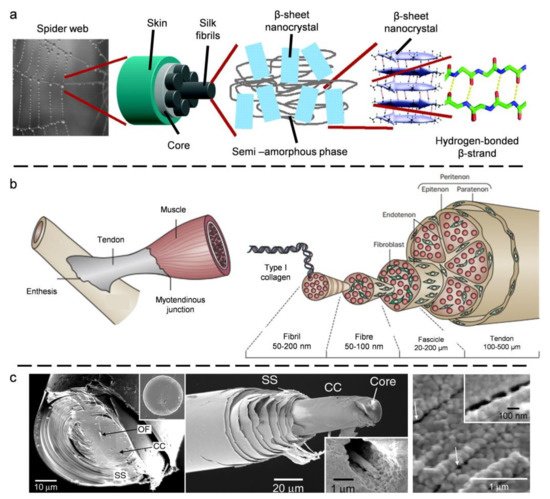
Coatings 11 01297 g002 550
Figure 2. (a) Schematic of the hierarchical spider silk structure that ranges from nano to macro. Reprinted with permission from [52], copyright 2010 ROYAL SOC. (b) Typical hierarchical structure of a tendon. Reprinted with permission from [55], copyright 2015 NATURE RESEARCH. (c) Structural and compositional characterization of the basalia spicules. Reprinted with permission from [56], copyright 2004 NATL ACAD SCIENCES.

2.2. Tendon

Like spider silk, tendons are high-performance biomaterials composed of protein fibers. Tendons are the connecting parts of muscles and bones. Tendons transfer loads from muscles to bones through their complex structures and respond to different mechanical loads [55]. In tendons, which is a tissue designed to carry uniaxial tension, fibers are aligned in one direction [11]. Tendons are made up of water, cells and extracellular matrix. A tendon has a hierarchical structure from the molecular scale to the entire tendon itself (Figure 2b) [57]. Tropocollagen components are ~1.5 nm in diameter, forming collagen microfibrils with a diameter of ~3.5 nm. The tropocollagen molecules attach to the adjacent molecules through intrafibrillar bonding. Collagen microfibrils are arranged into collagen subfiber (10~20 nm in diameter), which is also called primary fiber. Subfibers, in turn, arrange themselves into fibrils. Collagen fibers are bundles of collagen subfiber with diameters between 0.2 and 12 μm. Therefore, collagen fibers are also known as secondary fiber bundles. Further, collagen fibers make up collagen fascicle, which is also called a tertiary fiber bundle. Finally, the tendon is made up of multiple fascicles [55][57][58].
The tendon layer structure and mechanical properties of collagen are considered to be tendons’ structural foundation of the organization under mechanical load [57]. A functionally important feature of the tendon is its flexibility in bending. There is a crimped or wavy structure in the collagen fascicle, which has an important effect on the mechanical properties of the tendon [11][57]. Under the load, the crimps are pulled out and the fibrils become straight, but under low load, they are actually in effect pre-buckled on a microscale. Therefore, under zero load, the longitudinal tensile modulus and compression modulus are very small, and the longitudinal deformation required for bending also easily occurs [55]. Meyers et al. [11] calculated the expression of maximum strain that the collagen fibers can withstand without damage through an idealized configuration of wavy collagen fiber. Additionally, the loose binding of the fibers and higher levels of the hierarchy between each other causes the tendons to bend easily [59]. The interface between unidirectional collagen fibrils of the tendon also displays an important role in the deflection and blunting of incoming cracks and to channel deformations [60]. In addition to multiple dimensional changes in fiber structure, the amount of constituent substances is also arranged in a gradient [14]. In the area from the tendon fiber to the bone connection, the mineral content and crystallization order increase in sequence. This allows for a gradual change in the local hardness and elastic modulus at the tendon–bone interface, helping to adjust and transfer loads between different materials while minimizing stress concentrations.

2.3. Glass Sponge Spicules

Unlike spider silk and tendons mainly composed of proteins, sponges are marine organisms made of biological minerals with a 1D fibrous structure: spicule. Its shape, chemical constituents and structure are the basis of glass sponge animal classification. Skeletons made of calcium carbonate are in the class Calcarea, those with silica are in the class Hexactinellida and those of protein fibers (spongin) are in the class Demospongiae [12][61]. Inorganic glass sponge spicules are a good example of well-designed ceramic fibers. It shows high fracture resistance and high flexibility [29][62][63]. These excellent mechanical properties come from their structures. Reference [64] described the hierarchical structure of the sea sponge from a nanometer to macroscopic length scales. Bundles of spicules form fibers or struts of the cage. These spicules have a layered structure with three different regions [56]. An axial organic filament with a hollow core in the middle is firstly wrapped in a smooth central cylinder. Finally, they are embedded in a striated shell composed of a series of equally spaced layers (Figure 2c) [56]. Zlotnikov et al. [29] proved that the axial filament is a composite material by measuring the anchor spicule of sponge Monorhaphis chuni (M. chuni), which contains nearly equal volume fractions of biosilica and proteins. There is a thin layer of protein “glue” sandwiched between the mineral layers, which bonds these layers together. Further, each layer is composed of spherical nanoparticles (~100 nm), which are also aggregated by a protein called silicatein [65].
Walter et al. [66] and Miserez et al. [67] gave a detailed explanation of the toughening mechanism of the sponge spicules. Due to the existence of the organic layer in the SS region, the toughness of the spicules is improved. When the crack grows through the organic layer, it stops or shifts, which absorbs energy and makes the spicules tougher. If the fracture process continues, new cracks will form in adjacent silica layers. Due to the random nature of brittle fractures, cracks generally occur at locations that are not coplanar with the initial crack. This strategy of sacrificing stiffness makes the structure tougher and more flexible. Another benefit of the layered structure is that when bending occurs, the outermost thin silicon layer can be broken without affecting the whole fiber performance. This is because during the bending process, the outer layer is more curved than the inner layer. The thicker fibers in the inner layer make the fibers as rigid and strong as needed. However, in tension, each layer of fiber is subjected to a uniform load, meaning the fiber is not as tough as when in bending. In addition to outstanding mechanical properties, glass sponges also have significant fiber-optic properties that attracted attention [56]. This mechanism in sponge spicules shows excellent mechanical properties: the elastic modulus is 40.82 ± 9.65 GPa, fracture stress is 3727.12 ± 660.77 MPa and bending toughness is 69.45 ± 11.71 MPa [65].

3. Biological Models with 2D Layered Structures

Two-dimensional layered structures from composite materials with multiple layers or interfaces are usually used to improve the toughness. For example, glass sponge spicules with concentric silicon layers can be considered as a typical biological model with 2D layered structures in a sense [16]. Nacre is another well-known biological model with organic–inorganic layered structures, but due to its excellent interfacial properties, we discuss it in a later section [21]. Different from the 1D fibrous structures such as natural silk and spider silk, more microscopic nanofibers are arranged in a 2D layered structure in organisms. These structures often appear in tough organisms, such as human teeth [68] and the dactyl club of mantis shrimps, which are biological attack weapons [69][70]. Fish scales [71], the outer epidermis of arthropods and cardiac muscles have defensive and protective effects [72]. Although their structures are not the same, they all have a universal mechanism. Here, we mainly describe several typical 2D layered structures which increase strength and toughness in multiple directions by using many different angled fibers and other reinforcements. Specific examples include wood tracheid, compact bones and natural bouligand composites.

3.1. Wood Tracheid

Wood is a good example of how nature uses highly oriented fibers to form layered structures. The cellular structure of wood is composed of parallel hollow tubes (also called cells or tracheid) [18]. In the cell wall of tracheid, stiff cellulose microfibrils are embedded in the amorphous hemicellulose and lignin matrix to form cellulose macrofibrils with a 2D laminated structure. Cellulose molecules form semi-crystalline cellulose microfibers through covalent and hydrogen bonds. Additionally, microfibers are very stiff and strong, as a result of the alignment of the molecular backbone with the axis of the microfibers [30]. Figure 3a shows a single primary layer and three secondary layers of a tracheid in softwood xylem [14]. Here, the outermost layer, the middle layer and the innermost layer were denoted with S1, S2 and S3, respectively. As the principal load-bearing element, the S2 layer is the thickest and accounts for 80%–90% of the tracheid by weight. In this layer, cellulose microfibrils, hemicelluloses and lignin account for about 45%, 35% and 20% of the volume, respectively [21]. The angle between the fibrils and the tracheid axis is defined as the microfibril angle (MFA) [73]. In the primary cell wall, the MFA is random to achieve isotropic behavior in the cell wall plane. In the secondary layer, the MFA of S2 is the smallest, S3 is the second smallest and S1 is the largest, which endows wood with anisotropic mechanical properties [23][47][74]. The MFA of the S2 layer determines the mechanical properties of the wood, with smaller MFAs resulting in higher stiffness levels (Figure 3b) [47]. The size of the MFA is also related to the age of the tree. In mature trees, wood fibers with small MFAs form stiff trunks that can withstand wind loads. In young trees, large MFA fibers form flexible trunks that can cope with strong winds by bending [47].
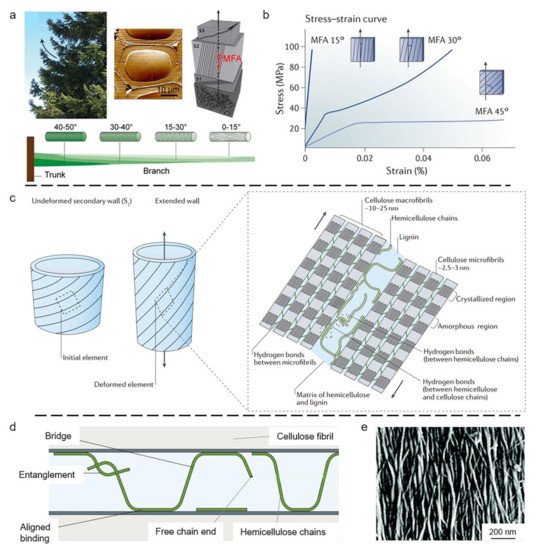
Coatings 11 01297 g003 550
Figure 3. (a) Digital photograph and schematic of a tracheid in wood xylem. Reprinted with permission from [14], copyright 2017 PERGAMON-ELSEVIER SCIENCE LTD. (b) The stress–strain curves of the cell wall with different MFAs. Reprinted with permission from [47], copyright 2018 NATURE RESEARCH. (c) The deformation mechanism of a wood tracheid. (d) Hemicellulose chain segments within the interfibrillar space. Reprinted with permission from [21], copyright 2016 NATURE RESEARCH. (e) SEM image of cellulose microfiber in S2 layer of Ginkgo xylem. Reprinted with permission from [69], copyright 2014 ROYAL SOC CHEMISTRY.
When loaded under tension along the direction of the tracheid, the S2 layer shows the yield point, and subsequently undergoes irreversible deformation, accompanied by a change in MFA [75]. However, after releasing the stress, the stiffness does not decrease with inelastic deformation [76][77]. The Velcro-like recovery mechanism at the interface between cellulose fibrils (Figure 3c) [21] can give a good explanation [76]. At the interface, hydrogen bonds can be formed between hemicellulose chains and cellulose fibrils, or between hemicellulose chains. The discontinuous hemicellulose bridge structure is formed by the hydrogen bond between cellulose fibrils and hemicellulose chains which align with cellulose fibrils. Entanglement is another configuration of the hemicellulose chain (Figure 3d,e) [69][76][78]. When the surface is under stress, part of the hydrogen bonds can be broken, and the hemicellulose chain is separated from cellulose fibrils. When the stress is released, the hemicellulose chain can re-approach and re-attach to the cellulose fibrils through hydrogen bonding to maintain the overall stiffness [21]. The middle lamella is another important interface in wood. It is responsible for connecting tracheid together. This thin interface is mainly composed of lignin, and it is weaker than tracheid walls. In the splitting mode, the weaker middle lamellae provide toughening mechanisms, such as crack deflection and fiber pullout. In this view, wood can be regarded as a fiber-reinforced composite, in which tracheids are fiber analogues and the middle lamellae are the matrix [21][31].

3.2. Compact Bone

Bone is featured with a coaxial layered staggered structure. It consists of cells and extracellular matrix. Bone is a bio-composite consisting of 60 wt.% minerals, 20–30 wt.% proteins and 10–20 wt.% water. Among the proteins, type I collagen accounts for 90%; the others are non-collagenous proteins [18]. There are two typical categories of bone: compact bone and spongy bone. Compact bone displays anisotropic behavior under compression and stretching behavior, which stems from the complexity of the hierarchical arrangement and the direction of bone structural components. Compact bone exhibits elastic-to-damage behavior under compressive load [79]. The behavioral characteristics of spongy bone under quasi-static compression load can divided into the initiation and growth of damage, and finally the fracture process in relatively narrow zones [80]. Compact bone has a complex hierarchical structure (Figure 4a) [8]. Collagen molecules (tropocollagen, ~300 nm in length and ~1.5 nm in diameter) and hydroxyapatite (HA) nanocrystals are periodically staggered and arranged into collagen fibrils parallel to the c-axis [81]. The individual collagen molecules interact through a hydrogen bond [21]. Collagen fibrils are stiff due to the arrangement of collagen molecules and the strengthening effect of HA nanocrystals [21]. The collagen fibers composed of bundles of collagen fibrils are arranged into cross plies and lamellae. Then, lamellae wrap around Haversian canals concentrically to form osteons [19]. The interface between osteons is called the cement line, which is composed of a high content of minerals and low content of collagen [81]. Osteons and the interface further form compact bone. The mechanical properties of compact bone are excellent, with elastic moduli of 15–20 GPa and tensile strengths of 100–160 MPa [82].
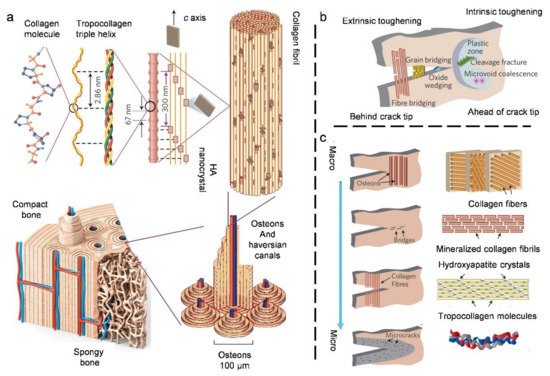
Coatings 11 01297 g004 550
Figure 4. (a) Hierarchical architecture of bone. (b) Intrinsic toughing mechanism and extrinsic toughing mechanism of the human bone to resist fracture. (c) The toughening mechanism from the macro scale to the nanoscale. Reprinted with permission from [8], copyright 2015 NATURE RESEARCH.
The excellent fracture resistance of bones can be explained from two perspectives: the intrinsic toughing mechanism and extrinsic toughing mechanism (Figure 4b) [8]. The intrinsic toughing mechanism mainly promotes ductility and acts on the micro-/nanoscale, including molecular uncoiling of the collagen components and the process of fibrillar sliding (most importantly) [32]. These fibrils are held together by a 1–2 nm-thickness layer of non-collagenous interfibrillar matrix, which is weaker and more compliant than aligned fibrils [21]. The proteins in the matrix are highly deformable and form ligament in the interface of collagen fibrils. It was experimentally observed that the shear at the interface between the collagen fibrils accounts for 60% of the total tensile deformation of the bone [33]. So, the interface of collagen fibrils is the key to energy dissipation. In addition to the ligament, osteocalcin in the non-collagenous interfibrillar matrix can also form sacrificial bonds with HA in the collagen fibrils. When the interface is sheared, the sacrificial bonds can be opened to provide molecular-scale displacement and can be quickly restored [34]. In addition to the sacrifice and ligament bridges mentioned above, the HA/collagen interface and intermolecular crosslinking also play roles in the process of fibrillar sliding [74]. When the fibrils slide, the fibril and the adjacent HA nanocrystals can create frictional resistance and thus hinder the sliding [83]. In bones, plasticity and ductility play a role in passivating the crack tip by dissipating energy and forming a plastic zone around the initial crack, thereby reducing the driving force of the crack and eventually toughening the material [8].
Compared with the intrinsic toughing mechanism, the extrinsic toughing mechanism has a greater contribution to the fracture resistance of bones, which mainly plays a role at a larger range (~10–100 μm). In essence, the extrinsic toughing mechanism mainly hinders crack growth, including crack bridging and crack deflection/twist [8]. The crack bridging mainly occurs at the tip of the crack propagation, forming an uncracked ligament bridging to suppress the crack propagation (Figure 4c) [8]. Crack deflection/twist mainly depends on the cement line, which is an interface between the osteons and the surrounding interstitial bone. Cement lines are more brittle and weaker because they mineralize more than the surrounding bone. When under load, bone can become tougher by deflecting or twisting the crack along the weaker cement line. Once the cement line breaks, friction will be generated, preventing the osteons from continuing to slide [84]. These extrinsic toughing mechanisms lead to resistance to both initiated and growing cracks [8].

3.3. Natural Bouligand Composites

The bouligand or twisted plywood is the most commonly observed 2D layered structure in natural materials. The constituent fibrils are arranged in layers stacked in a helical fashion to provide high levels mechanical strength and toughness [19]. The earliest creatures found to have bouligand structures were crustacean exoskeletons or cuticles (crab and lobster shells) [85]. The exoskeleton is made of CaCO3 and chitin–protein fibers and has a four-layer structure from top to bottom, which includes the epicuticle, procuticle (including the exocuticle and endocuticle) and underlying epidermal tissue [7][18]. The hierarchical structure of the exoskeleton is described in detail in [7]. The outermost epicuticle is a thin layer of a waxy surface composed of lipids and proteins, providing a water barrier for marine crustaceans. In addition, only the underlying epidermal tissue is not calcified. The procuticle with a hierarchical structure consisting of organic and inorganic components is the thickest and provides the main load-bearing properties [7][18]. First of all, N-acetyl-D-glucosamine grows in length to form long-chain polysaccharides polymers. Then, proteins and α-chitin molecules are linked by covalent bonds to form nanofibrils. Next, these nanofibrils wrapped in anionic proteins aggregate to form chitin–protein fibers. Finally, these fibers self-assemble to form a bouligand structure with helical stacking of horizontal fibers [7][18][20]. Yaraghi et al. [7] defined the pitch length as the repeat distance within a helicoidal structure over which the fiber layers produce a complete 180° rotation. In the procuticle, a decrease in the pitch length is observed from the cuticle surface toward the interior [86]. Besides, there are fibrous pore canal tubules aligned perpendicular to the cuticle surface and penetrating the rotating nanofibrils. These fibrous pore canal tubules form a system that transports ions after molting [35][87]. This hierarchical cuticle protects crustacean. The spiral arrangement of fibers creates a toughening effect by enhancing damage tolerance and energy absorption. The inherent elastic modulus oscillation of the spiral structure reduces the local driving force of crack propagation between layers [88]. In addition, because there is a difference in modulus between the mineral and the organic polymer in the mineralized fiber, the fiber interface can be toughened by crack deflection [7]. The crack also deflects along the path of the helicoidal structure, increasing the length of the crack path to consume a large amount of energy. The pore canal tubules perpendicular to the fiber layer form a structure similar to z-pinning to enhance the resistance to delamination between the fiber layers [7].
The scales of the Amazonian fish (Arapaima gigas) also have a similar bouligand structure that aids in resisting attacks [89]. Figure 5a shows the hierarchical structure of Amazonian arapaima fish scales [89]. In addition to a highly mineralized outer layer, the scales also have an inner lamellar layer made of spirally arranged fibril lamellae. These fibril lamellae are made up of mineralized collagen fibrils in the same direction and the fibrils are composed of collagen molecules and hydroxyapatite nanocrystal [36][89]. This special spiral structure causes the fibril lamella to reorient itself when subjected to external loads (Figure 5b) [89]. Most of the fibril lamellae are oriented toward the stretching axis and are found to be deformed under tension through the stretching or sliding mechanism, while other fibril lamellae are gradually rotated away from the stretching axis and exhibit a compression trend. It is this unique structure and its complex deformation mechanisms (such as stretching, rotation, delamination and compression) that make the arapaima fish scales resistant to damage [7][89][90].
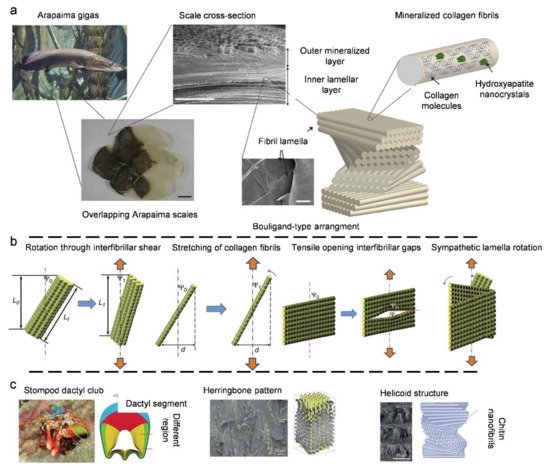
Coatings 11 01297 g005 550
Figure 5. (a) Hierarchical structure of Amazonian arapaima fish. Reprinted with permission from [89], copyright 2013 NATURE RESEARCH. (b) Deformation and rotation mechanisms of arapaima fish scales. Reprinted with permission from [89], copyright 2013 NATURE RESEARCH. (c) Structural features of the dactyl club of the peacock mantis shrimp Odontodactylus scyllarus. Reprinted with permission from [47], copyright 2018 NATURE RESEARCH.
The most prominent creature with a bouligand structure is the stomatopod dactyl club of the mantis shrimp (Odontodactylus scyllarus) [91]. When a mantis shrimp attacks prey, it can instantly hit the prey’s shell with its dactyl club, which can reach a speed of 23 m s−1, an acceleration over 105 m s−2 and a force up to 1500 N [37][91][92]. Thanks to its multi-level structure (Figure 5c) [47], the dactyl club can withstand thousands of repeated high-intensity impacts without being destroyed. The dactyl club is made up of the dactyl (D) segment and the propodus (P) segment. Figure 5c shows the cross-section of the club, including the impact region (blue), the medial periodic region (red), the lateral periodic region (yellow) and the striated region (green) [38]. The impact region consists of a hard external zone and a herringbone structure region. The external zone is composed of nano-apatites to provide hardness. The herringbone structure region features highly ordered, compacted and pitch-graded sinusoidal arrangements of helicoidally arranged chitin nanofibrils, which are covered with highly mineralized apatite. Additionally, the direction of apatite is parallel to the long axis of the chitin nanofibers. These unique structures provide the impact region with an anisotropic stiffness response and quasi-plastic behavior. When under compressive loading, this structure can enable stress redistribution and out-of-plane stiffness (that is, the stiffness along the x-direction of the herringbone pattern) [22][93]. Further, a modulus mismatch in the impact region can cause crack deflection to provide additional protection against damage [22][91]. The partially mineralized chitin nanofibril helicoidal structure forms a periodic region, and the periodic region, as the main energy absorbing layer, has the same mechanism as Crustacean exoskeletons [48].
Kellersztein and Wagner [94] compared the hierarchical structure and mechanical properties of the cuticles of the Scorpio maurus palmatus and the Buthus occitanus israelis. Figure 6a shows a schematic diagram of the structure of the chela cuticle [94]. Additionally, their group revealed a unique bouligand structure by observing the cuticle of the Scorpio maurus palmatus tarsus in detail [95]. There are 40–100 laminae of chitin–protein fibers embedded in the protein matrix to form the bouligand laminate unit (BLU). Compared with the classical bouligand structure, the BLU has the following two characteristics: off-axis helicity and dual-angle laminating (Figure 6b) [95]. The off-axis helicity means the laminae are twisted about their corners rather than centers, and dual-angle laminating means the laminae are tilted in addition to their twisting. The resulting BLU is highly warped, such that neighboring BLUs are intricately intertwined, tightly nested and mechanically interlocked. This structure significantly enhances the laminate flexural stiffness and strength and may improve toughness by diverting crack propagation.
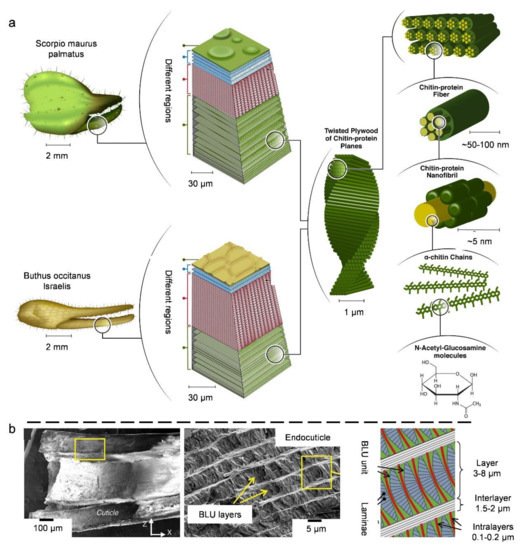
Coatings 11 01297 g006 550
Figure 6. (a) Schematic illustration of the hierarchical structure in the Scorpio maurus palmatus and the Buthus occitanus israelis chela cuticle. Reprinted with permission from [94], copyright 2019 ELSEVIER SCI LTD. (b) Bouligand laminate unit geometrical model compare with their biological counterparts. Reprinted with permission from [95], copyright 2020 NATURE RESEARCH.

4. Biological Models with 3D Cellular Structures

Many creatures require stiff and light-weight structures, especially birds. They have cellular elements in feathers, bones and beak structures. A common feature of such a structural design is a thin and dense exterior with a hollow or porous interior to resist external loads, which can provide strength while minimizing weight. The 3D interconnected structure of the dragonfly elytra has an anti-cracking effect, and also has excellent toughness, load-bearing capacity and fatigue resistance. This also provides protection for the wings and prevents air friction from breaking the dragonfly’s wings [96]. The structural parameters of the Cybister elytra also provide a reference for the design of sandwich composites [97]. Although many flying creatures have complex 3D cellular structures—the structure of birds has been studied especially deeply— hedgehog and porcupine spines also have similar structures with a defensive role. Here, we mainly introduce the typical 3D cellular structures in the beaks, bones and feathers of birds.

4.1. Bird Beaks

The toucan bird has a long and thick beak. The length of a toucan’s beak accounts for 1/3 of the bird’s total length, but thanks to its density being approximately 0.1 g/cm3, the mass is only one-twentieth of the total bird. Similar to the toucan, the hornbill’s beak occupies 1/4 of the bird’s total length and the density is about 0.3 g/cm3 [39][98][99]. Toucan and hornbill beaks are 3D cellular structures made of foam and covered with a hard surface [11]. This structure achieves the perfect fusion of low density and sufficient rigidity. Figure 7a, d show toucan and hornbill beaks schematically [11]. The hornbill’s beak has a unique casque formed from a cornified keratin layer [11][12][39]. The hard surface (keratin shell) of toucan and hornbill beaks consists of multiple layers of keratin scales (Figure 7e) [39]. The keratin scales are hexagonal, are glued together and overlap each other. Each keratin scale is about 50 µm in diameter, 1 µm in thickness and the total shell thickness is approximately 0.5 mm [39]. The intermediate filaments (fibers) are embedded in the keratin matrix and create a difference in orientation from one layer to the next. So, keratin is a protein-based fiber-reinforced composite material and the mineralization of calcium increases its hardness [12][39]. The viscoplastic response of the glue was shown to cause the keratin shell to exhibit a failure mode that was strain-rate dependent. When stretching at a strain rate of 5×10−5 /s, failure occurred due to the pullout of the scales. When at 1.5 × 10−5 /s, failure took place due to fracture of the scales [39]. Figure 7c,d shows the optical and SEM micrographs of toucan and hornbill beaks. The beak bone trabecula consists of an elliptical or cylindrical rod and the pores of the beak bone trabecula are sealed off by thin membranes [12][39]. Thus, it can be considered as a closed-cell foam, as defined by Gibson and Ashby [100]. This closed-cell foam is composed of fibers with higher calcium content, whose Young’s modulus is twice that of the keratin shell. Meanwhile, the membranes have a composition similar to the keratin shell [39]. The compressive response of the foam was successfully modeled by the Gibson–Ashby constitutive equation for closed-cell foam. It was found that because the density of hornbill foam is three times that of a hornbill’s beak, its strength is correspondingly higher [99][101]. The mechanical behavior of a complete beak is dominated by hard surfaces and foam. When the bird’s beak is loaded, most of the load is borne by exterior keratin, while the foam increases the energy absorption rate, stabilizes the deformation of the beak and prevents catastrophic damage. In addition, the hollow core makes the beak exhibit a high bending resistance [12][39].
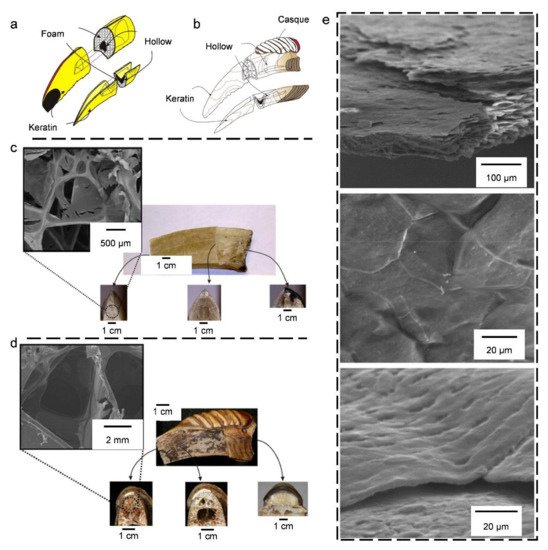
Coatings 11 01297 g007 550
Figure 7. (a,b) Schematics of the toucan beak and hornbill beak. Reprinted with permission from [11], copyright 2008 Elsevier. (c,d) Micro-images of the internal foam structures with three different cross-sections of toucan beak and hornbill beak. Reprinted with permission from [11], copyright 2008 Elsevier. (e) SEM images of the exterior of the beak (keratin) from different views. Reprinted with permission from [39], copyright 2005 PERGAMON-ELSEVIER SCIENCE LTD.

4.2. Bird Bones and Feather Shafts

Wing skeletons are particularly light, and most birds have hollow bones in their wings. These hollow bones can connect to the lung system and circulate air to increase bone buoyancy [12][102]. Because bird bones and feathers are subject to bending and torsional stress in flight, they have evolved similar structural characteristics: a thin, dense exterior with reinforcing internal structures [103]. Figure 8a shows the wing bones, which have a hollow and circular mid-cross section with struts [103]. These hollow bones have a thinner-walled structure and greater density than marrow-filled bones [104]. Similarly, the feather shaft has a thin, compact cortex and a hollow but foam-filled interior (Figure 8b) [103]. These lightweight structures (both in bones and feathers) with a tight outer and hollow interior are designed to resist external loads. When under bending loads, materials farther from the neutral axis can withstand more compression and extension than materials closer to the neutral axis. When under torsion, the thin-walled closed section provides a high torsional stiffness. In addition, the dense exterior wall also leads to an increase in structural stiffness [103][104]. Both bone and feathers have internal reinforcements: ridges, struts and foam (Figure 8c) [103]. To resist the tensile stress caused by torsion, the ridges are aligned at −45° to the horizontal axis of the bone. For feathers, the ridges occur on the dorsal surface for reinforcement because the dorsal side of the feather shaft is under the most pressure during the bird’s downstroke [103]. There are isolated rods called struts on the ventral side of the pneumatic bone to resist the combined bending and torsion load. The feather uses foam-filled rachis to resist local buckling and to absorb the bulk of energy [103]. Most of these medullary foams are closed-celled and the cell walls consist of porous fibers [103].
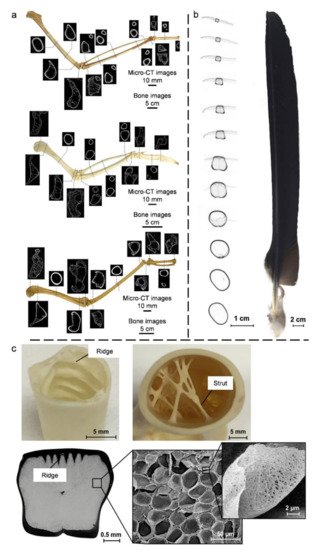
Coatings 11 01297 g008 550
Figure 8. (a) Micro-computerized tomography scan of different wing bones. (b) Micro-computerized tomography generated images of an Andean condor (Vultur gryphys) primary feather. (c) Internal reinforcements in the avian bone and feather: ridges and foam. Reprinted with permission from [103], copyright 2017 ELSEVIER SCI LTD.
Bird bone is a hierarchical structure composed of collagen and hydroxyapatite. The bone lamellae composed of fiber bundles are arranged in different orientations to resist bending and torsional loads (the same principle as the wood and bone mentioned in the previous section) [40]. The feather cortex is a fiber-reinforced composite with multiple layers of an organization composed exclusively of β-keratin. First, crystalline β-keratin filaments are embedded in amorphous matrix proteins. Then, keratin filaments are bundled to form macrofibrils, and macrofibrils are further organized into fibers. Finally, fibers form ordered lamellae in the feather shaft cortex [105][106]. The different arrangement directions of the fiber layers in the feather are used to resist different loads. The thicker inner longitudinal fibers form the skeleton of the feather shaft. In the vicinity of calamus, there is a thin outer layer composed of circumferentially wrapped fibers to prevent axial fiber separation during bending. There are ±45° cross-fiber layers on the lateral walls of the rachis to cope with the shear stress caused by bending and improve the torsional stiffness [106][107][108].

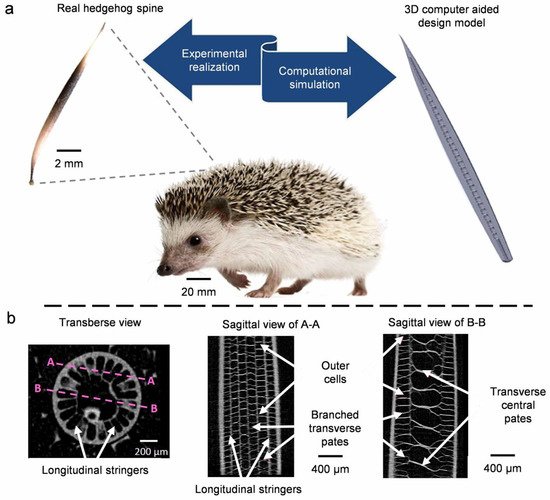
4.3. Quills

Some mammals, such as porcupines and hedgehogs, grow rough, hard, sharp hair for defense and protection. These quills are made of keratin and are structured as long tubes with tapered ends filled with a closed foam cell [12][13]. Porcupines can be divided into two main families: Old World (e.g., African porcupine) and New World (e.g., American porcupine) [13]. Old World porcupines have longer and thicker quills than New World ones [109][110][111]. The quill of the African porcupine has stiffeners attached to the cortex and gradually extends towards the center. The remaining area is filled with foam-like cells. Additionally, there are irregular scales on the surface cortex and stomata [111]. The cortex shell of the African porcupine quill is divided into three layers: a moderately ordered outer α-protein layer, a highly ordered middle α-protein layer, and an amorphous inner β-protein layer [112]. American porcupine quills have a closed foam core without struts inside. The cells in the center are large, while those near the cortex are small. American porcupine quills have overlapping keratin scales on the surface, forming a serrated structure that can be smoothly inserted, but is difficult to pull out [13]. North American porcupine quills show a clear fine filament–matrix structure. The longitudinal sections of quill tips show longitudinally oriented crystalline a-keratin intermediate filaments, which has a significant effect on the mechanical properties. The cortex carries the majority of the load, and the foam can withstand high tensile or compressive deformation to adapt to the buckling of the cortex [111][113]. Further, the cell collapse and cell densification of the inner foam core are the key to energy absorption during compression buckling [40].
Porcupine quills can bear considerable loads to pierce predators, while hedgehog spines (also known as quills) are famous for their excellent shock absorption performance (Figure 9a). The inner structure of hedgehog spines has two main structural features: the longitudinal stringers and the transverse central support plates (Figure 9b) [105]. Around the outer wall of the spine, there are 22 (this number is constant for all hedgehog spines) evenly distributed longitudinal stringers that run through the entire length of the spine, forming outer cells. The transverse central support plates are evenly distributed in the center of the spines. The transverse central support plates branch off into three thinner sections (called branched transverse plates) at the position in contact with the longitudinal stringers. The outer wall of the spine and the longitudinal stringers are connected by these branched transverse plates [105]. The thin-walled hollow structure of the hedgehog spines can reduce mass and increase torsional stiffness, but its bending resistance is weak. The longitudinal stringers compensate for the weak bending stiffness. Additionally, the support plate provides more structural support for the spine so that the stress is evenly distributed on the spine surface, preventing spine buckling and failing. These structures enable the spine to absorb more energy [41][109][114][115].
Coatings 11 01297 g009 550
Figure 9. (a) Digital photographs and modeling of a single spine of a hedgehog. (b) X-ray micro-computed tomography images of key features in a hedgehog spine with different sections. Reprinted with permission from [41], copyright 2019 ELSEVIER SCI LTD.

References

  1. Barthelat, F. Architectured materials in engineering and biology: Fabrication, structure, mechanics and performance. Int. Mater. Rev. 2016, 60, 413–430.
  2. Jiao, Z.B.; Chu, W.C.; Liu, L.P.; Mu, Z.Z.; Li, B.; Wang, Z.; Liao, Z.W.; Wang, Y.C.; Xue, H.; Niu, S.C.; et al. Underwater writable and heat-insulated paper with robust fluorine-free superhydrophobic coatings. Nanoscale 2020, 12, 8536–8545.
  3. Niu, S.C.; Li, B.; Ye, J.F.; Mu, Z.Z.; Zhang, J.Q.; Liu, Y.; Han, Z.W. Angle-dependent discoloration structures in wing scales of Morpho menelaus butterfly. Sci. China Technol. Sci. 2016, 59, 749–755.
  4. Han, Z.W.; Mu, Z.Z.; Li, B.; Feng, X.M.; Wang, Z.; Zhang, J.Q.; Niu, S.C.; Ren, L.Q. Bioinspired omnidirectional self-stable reflectors with multiscale hierarchical structures. ACS Appl. Mater. Interfaces. 2017, 9, 29285–29294.
  5. Ritchie, R.O. The conflicts between strength and toughness. Nat. Mater. 2011, 10, 817–822.
  6. Velasco-Hogan, A.; Xu, J.; Meyers, M.A. Additive manufacturing as a method to design and optimize bioinspired structures. Adv. Mater. 2018, 30, 1800940.
  7. Yaraghi, N.A.; Kisailus, D. Biomimetic structural materials: Inspiration from design and assembly. Annu. Rev. Phys. Chem. 2018, 69, 23–57.
  8. Wegst, U.G.; Bai, H.; Saiz, E.; Tomsia, A.P.; Ritchie, R.O. Bioinspired structural materials. Nat. Mater. 2015, 14, 23–36.
  9. Eder, M.; Amini, S.; Fratzl, P. Biological composites—Complex structures for functional diversity. Science 2018, 362, 543–547.
  10. Mao, L.B.; Gao, H.L.; Yao, H.B.; Liu, L.; Cölfen, H.; Liu, G.; Chen, S.M.; Li, S.K.; Yan, Y.X.; Liu, Y.Y. Synthetic nacre by predesigned matrix-directed mineralization. Science 2016, 354, 107–110.
  11. Meyers, M.A.; Chen, P.Y.; Lin, A.Y.M.; Seki, Y. Biological materials: Structure and mechanical properties. Prog. Mater. Sci. 2008, 53, 1–206.
  12. Chen, P.Y.; McKittrick, J.; Meyers, M.A. Biological materials: Functional adaptations and bioinspired designs. Prog. Mater. Sci. 2012, 57, 1492–1704.
  13. Wang, B.; Yang, W.; McKittrick, J.; Meyers, M.A. Keratin: Structure, mechanical properties, occurrence in biological organisms, and efforts at bioinspiration. Prog. Mater. Sci. 2016, 76, 229–318.
  14. Liu, Z.; Meyers, M.A.; Zhang, Z.; Ritchie, R.O. Functional gradients and heterogeneities in biological materials: Design principles, functions, and bioinspired applications. Prog. Mater. Sci. 2017, 88, 467–498.
  15. Yang, W.; Meyers, M.A.; Ritchie, R.O. Structural architectures with toughening mechanisms in Nature: A review of the materials science of Type-I collagenous materials. Prog. Mater. Sci. 2019, 103, 425–483.
  16. Naleway, S.E.; Porter, M.M.; McKittrick, J.; Meyers, M.A. Structural design elements in biological materials: Application to bioinspiration. Adv. Mater. 2015, 27, 5455–5476.
  17. Wang, J.; Cheng, Q.; Tang, Z. Layered nanocomposites inspired by the structure and mechanical properties of nacre. Chem. Soc. Rev. 2012, 41, 1600360.
  18. Frezzo, J.A.; Montclare, J.K. Natural composite systems for bioinspired materials. Adv. Exp. Med. Biol. 2016, 940, 143–166.
  19. Natarajan, B.; Gilman, J.W. Bioinspired Bouligand cellulose nanocrystal composites: A review of mechanical properties. Philos. Trans. R. Soc. A-Math. Phys. Eng. Sci. 2018, 376, 20170050.
  20. Zhao, H.; Yang, Z.; Guo, L. Nacre-inspired composites with different macroscopic dimensions: Strategies for improved mechanical performance and applications. NPG Asia Mater. 2018, 10, 1–22.
  21. Barthelat, F.; Yin, Z.; Buehler, M.J. Structure and mechanics of interfaces in biological materials. Nat. Rev. Mater. 2016, 1, 16007.
  22. Ren, J.; Wang, Y.; Yao, Y.; Wang, Y.; Fei, X.; Qi, P.; Lin, S.; Kaplan, D.L.; Buehler, M.J.; Ling, S. Biological material interfaces as inspiration for mechanical and optical material designs. Chem. Rev. 2019, 119, 12279–12336.
  23. Prabhakaran, R.T.D.; Spear, M.J.; Curling, S.; Wootton-Beard, P.; Jones, P.; Donnison, I.; Ormondroyd, G.A. Plants and architecture: The role of biology and biomimetics in materials development for buildings. Intell. Build. Int. 2019, 11, 178–211.
  24. Zhang, B.; Han, Q.; Zhang, J.; Han, Z.; Niu, S.; Ren, L. Advanced bio-inspired structural materials: Local properties determine overall performance. Mater. Today 2020, 41, 177–199.
  25. Mallick, P.K. Fiber-Reinforced Composites: Materials, Manufacturing, and Design; CRC Press: Boca Raton, FL, USA, 2007.
  26. Guan, Q.F.; Han, Z.M.; Zhu, Y.; Xu, W.L.; Yang, H.B.; Ling, Z.C.; Yan, B.; Yang, K.; Yin, C.; Wu, H.; et al. Bio-inspired lotus-fiber-like spiral hydrogel bacterial cellulose fibers. Nano Lett. 2021, 21, 952–958.
  27. Blackledge, T.A.; Hayashi, C.Y. Silken toolkits: Biomechanics of silk fibers spun by the orb web spider Argiope argentata (Fabricius 1775). J. Exp. Biol. 2006, 209, 2452–2461.
  28. Vehoff, T.; Glišović, A.; Schollmeyer, H.; Zippelius, A.; Salditt, T. Mechanical properties of spider dragline silk: Humidity, hysteresis, and relaxation. Biophys. J. 2007, 93, 4425–4432.
  29. Zlotnikov, I.; Masic, A.; Dauphin, Y.; Fratzl, P.; Zolotoyabko, E. Composition and mechanical properties of a protein/silica hybrid material forming the micron-thick axial filament in the spicules of marine sponges. Adv. Eng. Mater. 2014, 16, 1073–1077.
  30. Sinko, R.; Qin, X.; Keten, S. Interfacial mechanics of cellulose nanocrystals. MRS Bull. 2015, 40, 340–348.
  31. Thuvander, F.; Berglund, L.A. In situ observations of fracture mechanisms for radial cracks in wood. J. Mater. Sci. 2000, 35, 6277–6283.
  32. Launey, M.E.; Buehler, M.J.; Ritchie, R.O. On the mechanistic origins of toughness in bone. Ann. Rev. Mater. Res. 2010, 40, 25–53.
  33. Gupta, H.S.; Wagermaier, W.; Zickler, G.A.; Raz-Ben Aroush, D.; Funari, S.S.; Roschger, P.; Wagner, H.D.; Fratzl, P. Nanoscale deformation mechanisms in bone. Nano Lett. 2005, 5, 2108–2111.
  34. Fantner, G.E.; Hassenkam, T.; Kindt, J.H.; Weaver, J.C.; Birkedal, H.; Pechenik, L.; Cutroni, J.A.; Cidade, G.A.; Stucky, G.D.; Morse, D.E. Sacrificial bonds and hidden length dissipate energy as mineralized fibrils separate during bone fracture. Nat. Mater. 2005, 4, 612–616.
  35. Sachs, C.; Fabritius, H.; R-Aabe, D. Influence of microstructure on deformation anisotropy of mineralized cuticle from the lobster Homarus americanus. J. Struct. Biol. 2008, 161, 120–132.
  36. Lin, Y.; Wei, C.; Olevsky, E.; Meyers, M.A. Mechanical properties and the laminate structure of Arapaima gigas scales. J. Mech. Behav. Biomed. Mater. 2011, 4, 1145–1156.
  37. Patek, S.N.; Korff, W.; Caldwell, R.L. Biomechanics: Deadly strike mechanism of a mantis shrimp—This shrimp packs a punch powerful enough to smash its prey’s shell underwater. Nature 2004, 428, 819–820.
  38. Yaraghi, N.A.; Guarín-Zapata, N.; Grunenfelder, L.K.; Hintsala, E.; Bhowmick, S.; Hiller, J.M.; Betts, M.; Principe, E.L.; Jung, J.Y.; Sheppard, L. A sinusoidally architected helicoidal biocomposite. Adv. Mater. 2016, 28, 6835–6844.
  39. Seki, Y.; Schneider, M.S.; Meyers, M.A. Structure and mechanical behavior of a toucan beak. Acta Mater. 2005, 53, 5281–5296.
  40. De Margerie, E. Laminar bone as an adaptation to torsional loads in flapping flight. J. Anat. 2002, 201, 521–526.
  41. Drol, C.J.; Kennedy, E.B.; Hsiung, B.K.; Swift, N.B.; Tan, K.T. Bioinspirational understanding of flexural performance in hedgehog spines. Acta Biomater. 2019, 94, 553–564.
  42. Xi, S.; Tian, F.; Wei, G.; He, X.; Shang, Y.; Ju, Y.; Li, W.; Lu, Q.; Wang, Q. Reversible dendritic-crystal-reinforced polymer gel for bioinspired adaptable adhesive. Adv. Mater. 2021, 33, 2103174.
  43. Xu, X.; Li, L.; Seraji, S.M.; Liu, L.; Jiang, Z.; Xu, Z.; Li, X.; Zhao, S.; Wang, H.; Song, P. Bioinspired, strong, and tough nanostructured poly(vinyl alcohol)/inositol composites: How hydrogen-bond cross-linking works? Macromolecules 2021, 1c01725.
  44. Kono, N.; Nakamura, H.; Mori, M.; Yoshida, Y.; Ohtoshi, R.; Malay, A.D.; Moran, D.A.P.; Tomita, M.; Numata, K.; Arakawa, K. Multicomponent nature underlies the extraordinary mechanical properties of spider dragline silk. Proc. Natl. Acad. Sci. USA 2021, 3, e2107065118.
  45. Zan, G.; Wu, T.; Zhu, F.; He, P.; Cheng, Y.; Chai, S.; Wang, Y.; Huang, X.; Zhang, W.; Wan, Y.; et al. A biomimetic conductive super-foldable material. Matter 2021, 4, 3232–3247.
  46. Liu, C.; Li, B.; Li, Z.; Cao, C.; Gao, X.; Zhang, K.; Chen, H. 3D printable and fringe electric field adhesion enabled variable stiffness artificial muscles for semi-active vibration attenuation. Soft Matter 2021, 17, 6678–6902.
  47. Ling, S.J.; Kaplan, D.L.; Buehler, M.J. Nanofibrils in nature and materials engineering. Nat. Rev. Mater. 2018, 3, 18016.
  48. Nova, A.; Keten, S.; Pugno, N.M.; Redaelli, A.; Buehler, M.J. Molecular and nanostructural mechanisms of deformation, strength and toughness of spider silk fibrils. Nano Lett. 2010, 10, 2626–2634.
  49. Heim, M.; Römer, L.; Scheibel, T. Hierarchical structures made of proteins. The complex architecture of spider webs and their constituent silk proteins. Chem. Soc. Rev. 2010, 39, 156–164.
  50. Foelix, R. Biology of Spiders; OUP: Cary, NC, USA, 2011.
  51. Keten, S.; Xu, Z.; Ihle, B.; Buehler, M.J. Nanoconfinement controls stiffness, strength and mechanical toughness of β-sheet crystals in silk. Nat. Mater. 2010, 9, 359–367.
  52. Sinan, K.; Buehler, M.J. Nanostructure and molecular mechanics of spider dragline silk protein assemblies. J. R. Soc. Interface 2010, 7, 1709–1721.
  53. Asakura, T.; Suzuki, Y.; Nakazawa, Y.; Holland, G.P.; Yarger, J.L. Elucidating silk structure using solid-state NMR. Soft Matter 2013, 9, 11440–11450.
  54. Liu, R.; Deng, Q.; Yang, Z.; Yang, D.; Han, M.Y.; Liu, X.Y. “Nano-fishnet” structure making silk fibers tougher. Adv. Funct. Mater. 2016, 26, 5534–5541.
  55. Geoffroy, N.; Francis, B.; Delphine, D. Tendon injury: From biology to tendon repair. Nat. Rev. Rheumatol. 2015, 11, 223–233.
  56. Aizenberg, J.; Sundar, V.C.; Yablon, A.D.; Weaver, J.C.; Chen, G. Biological glass fibers: Correlation between optical and structural properties. Proc. Natl. Acad. Sci. USA 2004, 101, 3358–3363.
  57. Lipman, K.; Wang, C.; Ting, K.; Soo, C.; Zheng, Z. Tendinopathy: Injury, repair, and current exploration. Drug. Des. Devel. Ther. 2018, 12, 591–603.
  58. Watanabe, T.; Imamura, Y.; Hosaka, Y.; Ueda, H.; Takehana, K. Graded arrangement of collagen fibrils in the equine superficial digital flexor tendon. Connect. Tissue Res. 2007, 48, 332–337.
  59. Screen, H.; Bader, D.; Lee, D.; Shelton, J.J.S. Local strain measurement within tendon. Strain 2004, 40, 157–163.
  60. Ker, R.F. Mechanics of tendon, from an engineering perspective. Strain 2007, 29, 1001–1009.
  61. Müller, W.E.; Krasko, A.; Le Pennec, G.; Schröder, H.C. Biochemistry and cell biology of silica formation in sponges. Microsc. Res. Tech. 2003, 62, 368–377.
  62. Mayer, G. Mechanical energy dissipation in natural ceramic composites. J. Mech. Behav. Biomed. Mater. 2017, 76, 21–29.
  63. Drozdov, A.L.; Andreykin, N.A.; Dorofeev, A.G. Structure and physico-chemical properties of organosilicon crystal-like composite spicules of the glass sponge Hyalonema sieboldi. Mater. Res. Bull. 2018, 105, 372–376.
  64. Aizenberg, J.; Weaver, J.C.; Thanawala, M.S.; Sundar, V.C.; Morse, D.E.; Fratzl, P. Skeleton of Euplectella sp.: Structural hierarchy from the nanoscale to the macroscale. Science 2005, 309, 275–278.
  65. Cha, J.N.; Stucky, G.D.; Morse, D.E.; Deming, T.J. Biomimetic synthesis of ordered silica structures mediated by block copolypeptides. Nature 2000, 403, 289–292.
  66. Walter, S.L.; Flinn, B.D.; Mayer, G. Mechanisms of toughening of a natural rigid composite. Mater. Sci. Eng. C-Mater. Biol. Appl. 2007, 27, 570–574.
  67. Miserez, A.; Weaver, J.C.; Thurner, P.J.; Aizenberg, J.; Dauphin, Y.; Fratzl, P.; Morse, D.E.; Zok, F.W. Effects of laminate architecture on fracture resistance of sponge biosilica: Lessons from nature. Adv. Funct. Mater. 2008, 18, 1241–1248.
  68. Feng, Y.; Gao, H.L.; Wu, D.; Weng, Y.T.; Wang, Z.Y.; Yu, S.H.; Wang, Z. Biomimetic lamellar chitosan scaffold for soft gingival tissue regeneration. Adv. Funct. Mater. 2021, 31, 2105348.
  69. Han, Q.; Shi, S.; Liu, Z.; Han, Z.; Niu, S.; Zhang, J.; Qin, H.; Sun, Y.; Wang, J. Study on impact resistance behaviors of a novel composite laminate with basalt fiber for helical-sinusoidal bionic structure of dactyl club of mantis shrimp. Compos. Part B Eng. 2020, 191, 107976.
  70. Mohammadi, P.; Gandier, J.A.; Nonappa, N.; Wagermaier, W.; Miserez, A.; Penttilä, M. Bioinspired functionally graded composite assembled using cellulose nanocrystals and genetically engineered proteins with controlled biomineralization. Adv. Mater. 2021, 33, 2102658.
  71. Yin, S.; Yang, R.; Huang, Y.; Guo, W.; Chen, D.; Zhang, W.; Ren, M.; Zhou, Y.; Xu, J. Toughening mechanism of coelacanth-fish-inspired double-helicoidal composites. Compos. Sci. Technol. 2021, 205, 108650.
  72. Wang, Y.; Liao, W.; Sun, J.; Nandi, R.; Yang, Z. Bioinspired construction of artificial cardiac muscles based on liquid crystal elastomer fibers. Adv. Mater. Technol. 2021. online, 2100934.80.
  73. Lichtenegger, H.; Reiterer, A.; Stanzl-Tschegg, S.; Fratzl, P. Variation of cellulose microfibril angles in softwoods and hardwoods—A possible strategy of mechanical optimization. J. Struct. Biol. 1999, 128, 257–269.
  74. Xing, Y.; Jones, P.; Bosch, M.; Donnison, I.; Spear, M.; Ormondroyd, G. Exploring design principles of biological and living building envelopes: What can we learn from plant cell walls? Intell. Build. Int. 2018, 10, 78–102.
  75. Fratzl, P.; Burgert, I.; Keckes, J. Mechanical model for the deformation of the wood cell wall. Z. Metallk. 2004, 95, 579–584.
  76. Keckes, J.; Burgert, I.; Frühmann, K.; Müller, M.; Kölln, K.; Hamilton, M.; Burghammer, M.; Roth, S.V.; Stanzl-Tschegg, S.; Fratzl, P. Cell-wall recovery after irreversible deformation of wood. Nat. Mater. 2003, 2, 810–813.
  77. Spatz, H.; Kohler, L.; Niklas, K.J. Mechanical behaviour of plant tissues: Composite materials or structures? J. Exp. Biol. 1999, 202, 3269–3272.
  78. Altaner, C.; Jarvis, M.J. Modelling polymer interactions of the ‘molecular Velcro’ type in wood under mechanical stress. J. Theor. Biol. 2008, 253, 434–445.
  79. Ng, T.P.; Koloor, S.S.R.; Djuansjah, J.R.P.; Kadir, M.A. Assessment of compressive failure process of cortical bone materials using damage-based model. J. Mech. Behav. Biomed. Mater. 2017, 66, 1–11.
  80. Hambli, R. Micro-CT finite element model and experimental validation of trabecular bone damage and fracture. Bone 2013, 56, 363–374.
  81. Peng, J.; Cheng, Q. High-Performance Nanocomposites Inspired by Nature. Adv Mater. 2017, 29, 1702959.
  82. Blob, R.W.; Snelgrove, J.M.J.J.o.M. Antler stiffness in moose (Alces alces): Correlated evolution of bone function and material properties? J. Morphol. 2006, 267, 1075–1086.
  83. Tai, K.; Ulm, F.-J.; Ortiz, C. Nanogranular origins of the strength of bone. Nano Lett. 2006, 6, 2520–2525.
  84. Skedros, J.G.; Holmes, J.L.; Vajda, E.G.; Bloebaum, R.D. Cement lines of secondary osteons in human bone are not mineral-deficient: New data in a historical perspective. Anat. Rec. Part A Discov. Mol. Cell. Evol. Biol. Off. Publ. Am. Assoc. Anat. 2005, 286, 781–803.
  85. Bouligand, Y. Twisted fibrous arrangements in biological materials and cholesteric mesophases. Tissue Cell. 1972, 4, 189–217.
  86. Chen, P.Y.; Lin, A.Y.M.; McKittrick, J.; Meyers, M.A. Structure and mechanical properties of crab exoskeletons. Acta Biomater. 2008, 4, 587–596.
  87. Kunkel, J.G.; Nagel, W.; Jercinovic, M.J. Mineral fine structure of the American lobster cuticle. J. Shellfish Res. 2012, 31, 515–526.
  88. Nikolov, S.; Petrov, M.; Lymperakis, L.; Friák, M.; Sachs, C.; Fabritius, H.O.; Raabe, D.; Neugebauer, J. Revealing the design principles of high-performance biological composites using ab initio and multiscale simulations: The example of lobster cuticle. Adv. Mater. 2010, 22, 519–526.
  89. Zimmermann, E.A.; Gludovatz, B.; Schaible, E.; Dave, N.K.; Yang, W.; Meyers, M.A.; Ritchie, R.O. Mechanical adaptability of the Bouligand-type structure in natural dermal armour. Nat. Commun. 2013, 4, 1–7.
  90. Yang, W.; Sherman, V.R.; Gludovatz, B.; Mackey, M.; Zimmermann, E.A.; Chang, E.H.; Schaible, E.; Qin, Z.; Buehler, M.J.; Ritchie, R.O. Protective role of Arapaima gigas fish scales: Structure and mechanical behavior. Acta Biomater. 2014, 10, 3599–3614.
  91. Weaver, J.C.; Milliron, G.W.; Miserez, A.; Evans-Lutterodt, K.; Herrera, S.; Gallana, I.; Mershon, W.J.; Swanson, B.; Zavattieri, P.; DiMasi, E. The stomatopod dactyl club: A formidable damage-tolerant biological hammer. Science 2012, 336, 1275–1280.
  92. Patek, S.; Caldwell, R.L. Extreme impact and cavitation forces of a biological hammer: Strike forces of the peacock mantis shrimp Odontodactylus scyllarus. J. Exp. Biol. 2005, 208, 3655–3664.
  93. Amini, S.; Tadayon, M.; Idapalapati, S.; Miserez, A. The role of quasi-plasticity in the extreme contact damage tolerance of the stomatopod dactyl club. Nat. Mater. 2015, 14, 943–950.
  94. Kellersztein, I.; Cohen, S.R.; Bar-On, B.; Wagner, H.D. The exoskeleton of scorpions’ pincers: Structure and micro-mechanical properties. Acta Biomater. 2019, 94, 565–573.
  95. Greenfeld, I.; Kellersztein, I.; Wagner, H.D. Nested helicoids in biological microstructures. Nat. Commun. 2020, 11, 1–12.
  96. Meng, L.; Lan, X.; Zhao, J.; Hao, L.; Zemin, W.; Liang, G. Failure analysis of bio-inspired corrugated sandwich structures fabricated by laser powder bed fusion under three-point bending. Compos. Struct. 2021, 263, 113724.
  97. Xu, J.; Liu, T.; Zhang, Y.; Zhang, Y.; Wu, K.; Lei, C.; Qiang, F.; Fu, J. Dragonfly wing-inspired architecture makes a stiff yet tough healable material. Matter 2021, 4, 2474–2489.
  98. Seki, Y.; Kad, B.; Benson, D.; Meyers, M.A. The toucan beak: Structure and mechanical response. Mater. Sci. Eng. C-Mater. Biol. Appl. 2006, 26, 1412–1420.
  99. Seki, Y.; Bodde, S.G.; Meyers, M.A. Toucan and hornbill beaks: A comparative study. Acta Biomater. 2010, 6, 331–343.
  100. Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties; Cambridge University Press: Cambridge, UK, 1997.
  101. Meyers, M.A.; Lin, A.Y.; Seki, Y.; Chen, P.-Y.; Kad, B.K.; Bodde, S. Structural biological composites: An overview. JOM 2006, 58, 35–41.
  102. Cubo, J.; Casinos, A. Incidence and mechanical significance of pneumatization in the long bones of birds. Zool. J. Linn. Soc. 2000, 130, 499–510.
  103. Sullivan, T.N.; Wang, B.; Espinosa, H.D.; Meyers, M.A. Extreme lightweight structures: Avian feathers and bones. Mater. Today 2017, 20, 377–391.
  104. Dumont, E.R. Bone density and the lightweight skeletons of birds. Proc. R. Soc. B-Biol. Sci. 2010, 277, 2193–2198.
  105. Wang, B.; Sullivan, T.N. A review of terrestrial, aerial and aquatic keratins: The structure and mechanical properties of pangolin scales, feather shafts and baleen plates. J. Mech. Behav. Biomed. Mater. 2017, 76, 4–20.
  106. Wang, B.; Meyers, M.A. Light like a feather: A fibrous natural composite with a shape changing from round to square. Adv. Sci. 2017, 4, 1600360.
  107. Laurent, C.M.; Palmer, C.; Boardman, R.P.; Dyke, G.; Cook, R.B. Nanomechanical properties of bird feather rachises: Exploring naturally occurring fibre reinforced laminar composites. J. R. Soc. Interface. 2014, 11, 20140961.
  108. Wang, B.; Meyers, M.A. Seagull feather shaft: Correlation between structure and mechanical response. Acta Biomater. 2017, 48, 270–288.
  109. Vincent, J.F.; Owers, P. Mechanical design of hedgehog spines and porcupine quills. J. Zool. 1986, 210, 55–75.
  110. Karam, G.; Gibson, L.J. Biomimicking of animal quills and plant stems: Natural cylindrical shells with foam cores. Mater. Sci. Eng. C-Mater. Biol. Appl. 1994, 2, 113–132.
  111. Yang, W.; McKittrick, J. Separating the influence of the cortex and foam on the mechanical properties of porcupine quills. Acta Biomater. 2013, 9, 9065–9074.
  112. Busson, B.; Engström, P.; Doucet, J. Existence of various structural zones in keratinous tissues revealed by X-ray microdiffraction. J. Synchrot. Radiat. 1999, 6, 1021–1030.
  113. Chou, S.F.; Overfelt, R.A. Tensile deformation and failure of North American porcupine quills. Mater. Sci. Eng. C-Mater. Biol. Appl. 2011, 31, 1729–1736.
  114. Torres, F.G.; Troncoso, O.P.; Diaz, J.; Arce, D. Failure analysis of porcupine quills under axial compression reveals their mechanical response during buckling. J. Mech. Behav. Biomed. Mater. 2014, 39, 111–118.
  115. Swift, N.B.; Hsiung, B.K.; Kennedy, E.B.; Tan, K.T. Dynamic impact testing of hedgehog spines using a dual-arm crash pendulum. J. Mech. Behav. Biomed. Mater. 2016, 61, 271–282.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/)
Video Production Service
Feedback