
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Jianhan Chen | + 2966 word(s) | 2966 | 2021-10-09 11:02:58 | | | |
| 2 | Beatrix Zheng | + 212 word(s) | 3178 | 2021-10-25 05:16:58 | | | | |
| 3 | Beatrix Zheng | + 212 word(s) | 3178 | 2021-10-25 05:21:33 | | | | |
| 4 | Beatrix Zheng | + 212 word(s) | 3178 | 2021-10-25 05:32:28 | | | | |
| 5 | Beatrix Zheng | -1365 word(s) | 1813 | 2021-10-27 12:34:15 | | |
Video Upload Options
Intrinsically disordered proteins (IDPs) or regions (IDRs), compared to the well-structural proteins, do not have stable tertiary structures under physiological conditions, and even remain dynamic in specific complexes and functional assemblies. It is now recognized that they are highly prevalent and play important roles in biology and human diseases due to the presence of many representative conformational states and potential dynamic interactions, which requires computer simulations for describing disordered protein ensembles and dynamic interactions involved in biological functions, diseases, and therapeutics.
1. Significance and characterizations
IDPs or IDRs can be found in nearly a third of proteins encoded in the human proteome [1], and they play key roles in a variety of biological processes that underlie vital cellular functions ranging from signaling and regulation to transport [2][3]. The inherent thermodynamic instability of an IDP’s conformation allows it to respond sensitively to numerous stimuli, including binding, changes in cellular environments (e.g., pH), and post-translational modifications [4][5][6][7][8]. Such conformational plasticity arguably enables IDPs to interact with multiple signaling pathways and serve as scaffolds to form multi-protein complexes [9]. Importantly, IDPs and IDRs can have around 25% of disease-associated missense mutations [10]. They have been considered promising therapeutic targets for treating various diseases (such as chronic diseases) [11][12][13]. While many IDPs have been shown to undergo binding-induced folding transitions upon specific binding [3], many examples are also emerging to demonstrate that IDPs can remain unstructured even in specific complexes and functional assemblies [14][15][16][17][18][19][20]. Such a dynamic mode of specific protein interactions seems much more prevalent than previously thought [21][22][23].
Experimental ensemble-averaged characterizations
It is very challenging to provide reliable descriptions of the conformational ensembles of IDPs and IDRs. A disordered state does not lend itself to traditional structural determination methods that are geared toward describing a coherent set of similar structures. Biophysical techniques, such as NMR, SAXS, and FRET, can provide complementary information on various local and long-range structural organizations [7]. However, these ensemble-averaged measurements alone are not sufficient to unambiguously define the heterogeneous ensemble, due to the severely underdetermined nature of the structure calculation problem [8][24][25]. As a result, studies of IDPs have relied heavily in the traditional structure-function paradigm, by solving the folded structure of the bound state, analyzing coupled binding and folding mechanisms, or identifying putative pre-existing functional structures in the unbound state [3]. However, the disordered ensemble itself is arguably the central conduit of cellular signaling. The functional mechanism of an IDP is encoded in how the disordered ensemble as a whole responds to various stimuli, be it cooperative binding-induced folding or the redistribution of conformational sub-states in dynamic interactions. Multiple cellular signals can be naturally integrated through cooperative responses of the whole dynamic ensemble [26][27][28]. Therefore, there is a critical need for reliable characterization of disordered protein conformation ensembles, in both bound and unbound states, in order to establish the molecular basis of IDPs and IDRs in various physiological and pathophysiological processes.
Computational characterizations and simulations
Given the fundamental challenges of characterizing disordered protein states based on ensemble-averaged measurements alone, molecular modeling and simulations have a crucial and unique role to play in mechanistic studies of IDPs and IDRs [29][30][31][32][33]. This is reflected by the ever-increasing numbers of research articles in our research communities. A particularly attractive approach is to first generate the disordered ensemble using transferable, physics-based force fields without any experimental restraints and then use the later for independent validation [7]. Such de novo simulations of disordered protein ensembles require both high force field accuracy and adequate sampling of relevant conformational space, pushing the limit of these two central ingredients of molecular dynamics (MD) and Monte Carlo (MC) simulations. The challenges of simulating disordered proteins have driven significant interest in developing better protein force fields and advanced sampling methods. In particular, important advances have been made in the state-of-the-art atomistic force fields for describing the conformational equilibria of ordered and disordered proteins [13]. Enhanced sampling techniques have played crucial roles in both the development and application of atomistic force fields, by allowing one to cross energy barriers faster and accelerate the conformational sampling of IDPs [34][35][36][37][38][39][40][41]. Nonetheless, atomistic simulations still have limited capability in describing large systems such as biological condensates [42]. For this, multi-scale approaches are necessary to bridge the gaps in experimental and computational time- and length-scales, including implicit solvent models, which remove the solvent degrees of freedom [8], and various coarse-grained models, which significantly reduce both proteins and solvent degrees of freedom [43].
2. Simulating IDP conformations and dynamic interactions
Accurate force fields for High-dimensional free energy landscape
Compared to the globular proteins that have one or a few well-defined global energy minima, the energy landscape of an IDP is flatter and generally includes many local energy minima separated by modest energy barriers [44]. IDPs and IDRs typically have fewer hydrophobic residues, but a larger number of polar or charged as well as disorder-promoting residues (such as glycine and proline) [45]. These sequence features hamper the formation of hydrophobic cores that drive protein folding and thus prevent the formation of stable tertiary structures. Instead, IDPs and IDRs favor forming an ensemble of unfolded or partially folded states. This presents a major challenge for simulation and depends critically on the ability of the force fields to accurately describe the energetics of relevant conformational states, especially for capturing both folded and unfolded states of an IDP. For example, one recent study tested atomistic simulations of IDPs for eight force fields and found marked differences in the describing the conformational ensembles of IDPs, in particular the secondary structure content [46]. Similar observations have also been made in other benchmark studies, consistently showing that protein force fields previously optimized for folded proteins are not suitable for simulating disordered protein states, largely due to over-stabilization of protein-protein interactions [47]. These benchmark studies also suggested that the key towards better protein force field was to rebalance protein–protein, protein–water, and water–water interactions. Moreover, it can be also anticipated that polarizable force fields will be needed and become increasingly important for simulating IDP structure and interactions, because they explicitly consider the electronic polarization using various empirical models to provide better description of charged and polar protein motifs in heterogeneous biomolecular environments [48].
Advanced sampling for many relevant conformations
Besides accurate force fields, reliable simulation of IDPs also hinges on sufficient sampling of many relevant conformation states within a reasonable simulation time (Figure 1). Standard MD simulations are generally insufficient to generate representative conformational ensembles, even using the most accurate protein force fields coupled with advance of GPU computing or specialized hardware such as the ANTON supercomputer [49]. For example, a recent reanalysis of a 30-μs ANTON trajectory of a 40-residue Aβ40 peptide in explicit solvent revealed very limited convergence even at the secondary structure level [13]. This can be attributed to the diverse and large accessible conformational space of an IDP and the potentially high free energy barriers separating various sub-states that require exponentially longer time to cross. Note that typical simulation times on conventional hardware (such as GPUs) are at least one-order of magnitude shorter. There is thus great danger in relying on standard MD to calculate disordered protein conformational ensembles at the atomistic level. There is a critical need to develop and leverage so-called enhanced sampling techniques, which aim to generate statistically meaningful conformational ensembles with dramatically less computation. Representative enhanced methods have been proposed by introducing bias potentials, changing the effective temperature, or using the protocols of replica exchange molecular dynamics (REMD). Importantly, all biased sampling strategies can be readily incorporated within the REX framework to benefit from both classes of enhanced sampling, including metadynamics (MTD) [50][51], accelerated MD (aMD) [52], umbrella sampling (US) [53][54], and integrated tempering sampling [55]. It has been reported that these sampling methods can accelerate the crossing of energy barriers to achieve better sampling efficiency and have been used to sample the IDP conformations and dynamic interactions.
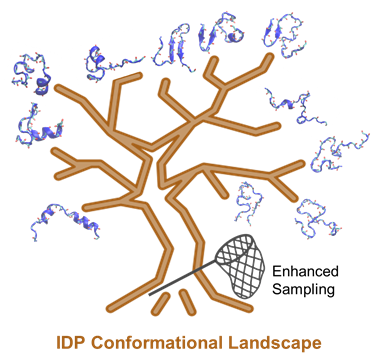
Figure 1. Simulating IDP conformational dynamics and interactions requires both the state-of-the-art force fields and advanced sampling methods.
Additionally, many key multi-scale approaches allow one to simulate longer time-scale bioprocesses and more complex systems within the capacity of current computational capability, namely implicit solvent and coarse-grained (CG) models. Implicit treatment of solvent is an effective approach to reduce the computational cost of atomistic IDP simulations. The basic idea is to directly estimate the solvation free energy to capture the mean effect of solvent on the thermodynamic properties of the solute [56]. Implicit solvent is essentially a multi-scale model, where the solvent is represented using certain physical model while keeping atomistic details of the solute. These models have emerged as attractive alternatives for simulations of IDPs and their interactions compared to explicit solvent. Several of these GB models can be optimized to provide a balance between computational efficiency and accuracy desired for IDP simulations [57][58][59], by systematic optimization of key physical parameters such as atomic radii to balance solvation and intramolecular interactions. Applied to various model IDPs with extensive experimental data, implicit solvent simulations have provided important insights on detailed conformational properties of the unbound state and how these properties may support function [32][33][60][61][62].
The coarse-graining has also remained an attractive and often effective strategy for extending the accessible time and length-scales of MD simulations. By grouping multiple (protein) atoms into CG beads and using simplified potential energy functions, CG modeling does not only reduce the system size, often by ~10-fold, but also allows much larger MD integration time steps up to 20 fs. Together, many CG models can be several orders of magnitude more efficient than atomistic ones. Numerous CG models have achieved varying levels of success in studies of protein folding, binding, and assembly [43][63]. Nonetheless, there are important distinctions between the conformational properties between globular proteins and IDPs, as well as the relative importance of electrostatic, hydrophobic, and hydrogen-bonding interactions in governing their conformational equilibria. Therefore, CG models optimized for the folded proteins are generally not suitable for the IDP simulations. It is often necessary to readjust the parameters of protein–protein and protein–solvent interactions or add new terms for more accurate description of IDP conformations.
Long-time simulations of IDP interactions and assembly
Computational studies of IDP interaction and assembly are even more demanding. The conformational equilibrium of an IDP can respond sensitively to specific and nonspecific binding, potentially shifting from a disordered to somewhat ordered state or fully folded state. In principle, simulations could provide the much-needed spatial and time resolutions to elucidate the kinetics and thermodynamics of coupled folding and binding processes and characterize the mechanistic features. However, the challenge is that this coupled process of folding and binding is a complex reaction involving the formation of many noncovalent interactions, which requires extremely long simulations generally beyond the current capabilities at the atomistic level. As such, coarse-grained models are generally required for computational studies of IDP interaction and assembly. For example, they have been used to study many biological processes, including liquid-liquid phase transitions (LLPS) that are frequently mediated by IDPs [29][45][64][65].
References
- Csizmok, V.; Follis, A.V.; Kriwacki, R.W.; Forman-Kay, J.D. Dynamic Protein Interaction Networks and New Structural Paradigms in Signaling. Chem. Rev. 2016, 116, 6424–6462.
- Oldfield, C.J.; Dunker, A.K. Intrinsically Disordered Proteins and Intrinsically Disordered Protein Regions. Annu. Rev. Biochem. 2014, 83, 553–584.
- Wright, P.E.; Dyson, H.J. Intrinsically disordered proteins in cellular signalling and regulation. Nat. Rev. Mol. Cell Biol. 2015, 16, 18–29.
- Uversky, V.N. Intrinsically disordered proteins and their (disordered) proteomes in neurodegenerative disorders. Front. Aging Neurosci. 2015, 7, 18.
- Dyson, H.J.; Wright, P.E. Intrinsically unstructured proteins and their functions. Nat. Rev. Mol. Cell Biol. 2005, 6, 197–208.
- Owen, I.; Shewmaker, F. The Role of Post-Translational Modifications in the Phase Transitions of Intrinsically Disordered Proteins. Int. J. Mol. Sci. 2019, 20, 5501.
- Chen, J. Towards the physical basis of how intrinsic disorder mediates protein function. Arch. Biochem. Biophys. 2012, 524, 123–131.
- Das, R.K.; Ruff, K.M.; Pappu, R.V. Relating sequence encoded information to form and function of intrinsically disordered proteins. Curr. Opin. Struct. Biol. 2015, 32, 102–112.
- Hatos, A.; Hajdu-Soltesz, B.; Monzon, A.M.; Palopoli, N.; Alvarez, L.; Aykac-Fas, B.; Bassot, C.; Benitez, G.I.; Bevilacqua, M.; Chasapi, A.; et al. DisProt: Intrinsic protein disorder annotation in 2020. Nucleic Acids Res. 2020, 48, D269–D276.
- Vacic, V.; Iakoucheva, L.M. Disease mutations in disordered regions—Exception to the rule? Mol. Biosyst. 2012, 8, 27–32.
- Kulkarni, P.; Uversky, V.N. Intrinsically Disordered Proteins in Chronic Diseases. Biomolecules 2019, 9, 147.
- Oldfield, C.J.; Cheng, Y.; Cortese, M.S.; Brown, C.J.; Uversky, V.N.; Dunker, A.K. Comparing and Combining Predictors of Mostly Disordered Proteins. Biochemistry 2005, 44, 1989–2000.
- Chen, J.; Liu, X.; Chen, J. Targeting Intrinsically Disordered Proteins through Dynamic Interactions. Biomolecules 2020, 10, 743.
- Mittag, T.; Marsh, J.; Grishaev, A.; Orlicky, S.; Lin, H.; Sicheri, F.; Tyers, M.; Forman-Kay, J.D. Structure/Function Implications in a Dynamic Complex of the Intrinsically Disordered Sic1 with the Cdc4 Subunit of an SCF Ubiquitin Ligase. Structure 2010, 18, 494–506.
- McDowell, C.; Chen, J.; Chen, J. Potential Conformational Heterogeneity of p53 Bound to S100B(betabeta). J. Mol. Biol. 2013, 425, 999–1010.
- Wu, H.; Fuxreiter, M. The Structure and Dynamics of Higher-Order Assemblies: Amyloids, Signalosomes, and Granules. Cell 2016, 165, 1055–1066.
- Krois, A.S.; Ferreon, J.C.; Martinez-Yamout, M.A.; Dyson, H.J.; Wright, P.E. Recognition of the disordered p53 transactivation domain by the transcriptional adapter zinc finger domains of CREB-binding protein. Proc. Natl. Acad. Sci. USA 2016, 113, E1853–E1862.
- Csizmok, V.; Orlicky, S.; Cheng, J.; Song, J.; Bah, A.; Delgoshaie, N.; Lin, H.; Mittag, T.; Sicheri, F.; Chan, H.S.; et al. An allosteric conduit facilitates dynamic multisite substrate recognition by the SCFCdc4 ubiquitin ligase. Nat. Commun. 2017, 8, 13943.
- Borgia, A.; Borgia, M.B.; Bugge, K.; Kissling, V.M.; Heidarsson, P.O.; Fernandes, C.B.; Sottini, A.; Soranno, A.; Buholzer, K.J.; Nettels, D.; et al. Extreme disorder in an ultrahigh-affinity protein complex. Nature 2018, 555, 61–66.
- Clark, S.; Myers, J.B.; King, A.; Fiala, R.; Novacek, J.; Pearce, G.; Heierhorst, J.; Reichow, S.L.; Barbar, E.J. Multivalency regulates activity in an intrinsically disordered transcription factor. Elife 2018, 7, e36258.
- Fuxreiter, M. Fuzziness in Protein Interactions-A Historical Perspective. J. Mol. Biol. 2018, 430, 2278–2287.
- Weng, J.; Wang, W. Dynamic multivalent interactions of intrinsically disordered proteins. Curr. Opin. Struct. Biol. 2019, 62, 9–13.
- Miskei, M.; Antal, C.; Fuxreiter, M. FuzDB: Database of fuzzy complexes, a tool to develop stochastic structure-function relationships for protein complexes and higher-order assemblies. Nucleic Acids Res. 2017, 45, D228–D235.
- Ganguly, D.; Chen, J. Structural interpretation of paramagnetic relaxation enhancement-derived distances for disordered protein states. J. Mol. Biol. 2009, 390, 467–477.
- Fisher, C.K.; Stultz, C.M. Constructing ensembles for intrinsically disordered proteins. Curr. Opin. Struct. Biol. 2011, 21, 426–431.
- Ferreon, A.C.; Ferreon, J.C.; Wright, P.E.; Deniz, A.A. Modulation of allostery by protein intrinsic disorder. Nature 2013, 498, 390–394.
- Garcia-Pino, A.; Balasubramanian, S.; Wyns, L.; Gazit, E.; De Greve, H.; Magnuson, R.D.; Charlier, D.; van Nuland, N.A.; Loris, R. Allostery and intrinsic disorder mediate transcription regulation by conditional cooperativity. Cell 2010, 142, 101–111.
- Berlow, R.B.; Dyson, H.J.; Wright, P.E. Expanding the Paradigm: Intrinsically Disordered Proteins and Allosteric Regulation. J. Mol. Biol. 2018, 430, 2309–2320.
- Levine, Z.A.; Shea, J.-E. Simulations of disordered proteins and systems with conformational heterogeneity. Curr. Opin. Struct. Biol. 2017, 43, 95–103.
- Knott, M.; Best, R.B. A preformed binding interface in the unbound ensemble of an intrinsically disordered protein: Evidence from molecular simulations. PLoS Comput. Biol. 2012, 8, e1002605.
- Mao, A.H.; Crick, S.L.; Vitalis, A.; Chicoine, C.L.; Pappu, R.V. Net charge per residue modulates conformational ensembles of intrinsically disordered proteins. Proc. Natl. Acad. Sci. USA 2010, 107, 8183–8188.
- Ganguly, D.; Chen, J. Atomistic details of the disordered states of KID and pKID. implications in coupled binding and folding. J. Am. Chem. Soc. 2009, 131, 5214–5223.
- Zhang, W.; Ganguly, D.; Chen, J. Residual structures, conformational fluctuations, and electrostatic interactions in the synergistic folding of two intrinsically disordered proteins. PLoS Comput. Biol. 2012, 8, e1002353.
- Zhang, W.; Chen, J. Accelerate Sampling in Atomistic Energy Landscapes Using Topology-Based Coarse-Grained Models. J. Chem. Theory Comput. 2014, 10, 918–923.
- Moritsugu, K.; Terada, T.; Kidera, A. Scalable free energy calculation of proteins via multiscale essential sampling. J. Chem. Phys. 2010, 133, 224105.
- Sugita, Y.; Okamoto, Y. Replica-exchange molecular dynamics method for protein folding. Chem. Phys. Lett. 1999, 314, 141–151.
- Liu, P.; Kim, B.; Friesner, R.A.; Berne, B.J. Replica exchange with solute tempering: A method for sampling biological systems in explicit water. Proc. Natl. Acad. Sci. USA 2005, 102, 13749–13754.
- Mittal, A.; Lyle, N.; Harmon, T.S.; Pappu, R.V. Hamiltonian Switch Metropolis Monte Carlo Simulations for Improved Conformational Sampling of Intrinsically Disordered Regions Tethered to Ordered Domains of Proteins. J. Chem. Theory Comput. 2014, 10, 3550–3562.
- Peter, E.K.; Shea, J.E. A hybrid MD-kMC algorithm for folding proteins in explicit solvent. Phys. Chem. Chem. Phys. 2014, 16, 6430–6440.
- Zhang, C.; Ma, J. Enhanced sampling and applications in protein folding in explicit solvent. J. Chem. Phys. 2010, 132, 244101.
- Zheng, L.Q.; Yang, W. Practically Efficient and Robust Free Energy Calculations: Double-Integration Orthogonal Space Tempering. J. Chem. Theory Comput. 2012, 8, 810–823.
- Best, R.B. Computational and theoretical advances in studies of intrinsically disordered proteins. Curr. Opin. Struct. Biol. 2017, 42, 147–154.
- Kmiecik, S.; Gront, D.; Kolinski, M.; Wieteska, L.; Dawid, A.E.; Kolinski, A. Coarse-Grained Protein Models and Their Applications. Chem. Rev. 2016, 116, 7898–7936.
- Arai, M. Unified understanding of folding and binding mechanisms of globular and intrinsically disordered proteins. Biophys. Rev. 2018, 10, 163–181.
- Bhattacharya, S.; Lin, X. Recent Advances in Computational Protocols Addressing Intrinsically Disordered Proteins. Biomolecules 2019, 9, 146.
- Rauscher, S.; Gapsys, V.; Gajda, M.J.; Zweckstetter, M.; de Groot, B.L.; Grubmüller, H. Structural Ensembles of Intrinsically Disordered Proteins Depend Strongly on Force Field: A Comparison to Experiment. J. Chem. Theory Comput. 2015, 11, 5513–5524.
- Best, R.B.; Zhu, X.; Shim, J.; Lopes, P.E.; Mittal, J.; Feig, M.; Mackerell, A.D., Jr. Optimization of the additive CHARMM all-atom protein force field targeting improved sampling of the backbone phi, psi and side-chain chi(1) and chi(2) dihedral angles. J. Chem. Theory Comput. 2012, 8, 3257–3273.
- Jing, Z.; Liu, C.; Cheng, S.Y.; Qi, R.; Walker, B.D.; Piquemal, J.-P.; Ren, P. Polarizable Force Fields for Biomolecular Simulations: Recent Advances and Applications. Annu. Rev. Biophys. 2019, 48, 371–394.
- Robustelli, P.; Piana, S.; Shaw, D.E. Developing a molecular dynamics force field for both folded and disordered protein states. Proc. Natl. Acad. Sci. USA 2018, 115, E4758–E4766.
- Barducci, A.; Bonomi, M.; Parrinello, M. Metadynamics. WIREs Comput. Mol. Sci. 2011, 1, 826–843.
- Barducci, A.; Bussi, G.; Parrinello, M. Well-Tempered Metadynamics: A Smoothly Converging and Tunable Free-Energy Method. Phys. Rev. Lett. 2008, 100, 020603.
- Hamelberg, D.; Mongan, J.; McCammon, J.A. Accelerated molecular dynamics: A promising and efficient simulation method for biomolecules. J. Chem. Phys. 2004, 120, 11919–11929.
- Torrie, G.M.; Valleau, J.P. Nonphysical sampling distributions in Monte Carlo free-energy estimation: Umbrella sampling. J. Comput. Phys. 1977, 23, 187–199.
- Kästner, J. Umbrella sampling. WIREs Comput. Mol. Sci. 2011, 1, 932–942.
- Gao, Y.Q. An integrate-over-temperature approach for enhanced sampling. J. Chem. Phys. 2008, 128, 064105.
- Chen, J.; Brooks, C.L.; Khandogin, J. Recent advances in implicit solvent based methods for biomolecular simulations. Curr. Opin. Struct. Biol. 2008, 18, 140–148.
- Lee, K.H.; Chen, J.H. Optimization of the GBMV2 implicit solvent force field for accurate simulation of protein conformational equilibria. J. Comput. Chem. 2017, 38, 1332–1341.
- Chen, J.; Im, W.; Brooks, C.L. Balancing solvation and intramolecular interactions: Toward a consistent generalized born force field. J. Am. Chem. Soc. 2006, 128, 3728–3736.
- Chen, J.; Brooks, C.L. Implicit modeling of nonpolar solvation for simulating protein folding and conformational transitions. Phys. Chem. Chem. Phys. 2008, 10, 471–481.
- Chen, J. Intrinsically disordered p53 extreme C-terminus binds to S100B(betabeta) through “fly-casting”. J. Am. Chem. Soc. 2009, 131, 2088–2089.
- Wang, Y.; Fisher, J.C.; Mathew, R.; Ou, L.; Otieno, S.; Sublet, J.; Xiao, L.; Chen, J.; Roussel, M.F.; Kriwacki, R.W. Intrinsic disorder mediates the diverse regulatory functions of the Cdk inhibitor p21. Nat. Chem. Biol. 2011, 7, 214–221.
- Ganguly, D.; Chen, J. Modulation of the disordered conformational ensembles of the p53 transactivation domain by cancer-associated mutations. PLoS Comput. Biol. 2015, 11, e1004247.
- Pak, A.J.; Voth, G.A. Advances in coarse-grained modeling of macromolecular complexes. Curr. Opin. Struct. Biol. 2018, 52, 119–126.
- Wang, W. Recent advances in atomic molecular dynamics simulation of intrinsically disordered proteins. Phys. Chem. Chem. Phys. 2021, 23, 777–784.
- Shea, J.-E.; Best, R.B.; Mittal, J. Physics-based computational and theoretical approaches to intrinsically disordered proteins. Curr. Opin. Struct. Biol. 2021, 67, 219–225.




