Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Aljaž Gaber
 + 1153 word(s) 1153 2021-09-04 11:36:20 |
2 format correct
Conner Chen
 Meta information modification 1153 2021-09-23 02:53:49 |

Video Upload Options

We provide professional Video Production Services to translate complex research into visually appealing presentations. Would you like to try it?
No, upload directly Yes

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Gaber, A. Homo-Oligomeric Proteins. Encyclopedia. Available online: https://encyclopedia.pub/entry/14300 (accessed on 25 November 2024).
Gaber A. Homo-Oligomeric Proteins. Encyclopedia. Available at: https://encyclopedia.pub/entry/14300. Accessed November 25, 2024.
Gaber, Aljaž. "Homo-Oligomeric Proteins" Encyclopedia, https://encyclopedia.pub/entry/14300 (accessed November 25, 2024).
Gaber, A. (2021, September 17). Homo-Oligomeric Proteins. In Encyclopedia. https://encyclopedia.pub/entry/14300
Gaber, Aljaž. "Homo-Oligomeric Proteins." Encyclopedia. Web. 17 September, 2021.
Homo-Oligomeric Proteins
Edit
This entry is adapted from the peer-reviewed paper 10.3390/ijms22169081

Protein homo-oligomerization is a very common phenomenon, and approximately half of proteins form homo-oligomeric assemblies composed of identical subunits. Many proteins have a natural tendency to self-associate into homo-oligomeric protein complexes, also termed homomers, which are composed of two or more identical subunits. According to the estimation, 30–50% of all proteins oligomerize. In addition, analysis of protein crystal structures demonstrated that roughly 45% of eukaryotic proteins and 60% of prokaryotic proteins that are deposited as single polypeptide chains also exist in a form of homo-oligomeric complex. 

Homo-Oligomeric Proteins homo-oligomers

1. Protein Homo-Oligomerization as an Efficient Design Principle

Homo-oligomerization is believed to be nature’s solution to form large proteins by avoiding efficiency problems with the synthesis of long polypeptide chains. In comparison to small proteins, larger ones are more favorable due to their higher stability and smaller solvent-exposed surface percentage. Moreover, building larger protein complexes from smaller subunits has several benefits. Such complexes are less prone to translational errors, as only the defected subunits can be discarded and replaced in contrast to the whole large single polypeptide-chain protein. Next, coding efficiency is higher because less information needs to be stored to build a large protein. Furthermore, assembly of (homo)-oligomeric proteins can be triggered and/or fine-tuned and thus provides an additional layer of regulation, which is crucial in dynamic processes such as actin filament assembly [1] and microtubule growth [2]. Other examples are protein activation as a consequence of dimerization, as in the case of caspase-9 activity [3] and signaling via epidermal growth factor receptor (EGFR) [4]. Additionally, an opposite effect can be achieved—for example, dimerization inhibits the activity of receptor-like protein tyrosine phosphatase-a [5]. Even more prominent examples are where the active site is formed at the interface between subunits, as in the case of HIV-1 dimerization protease. [6]. Besides, oligomerization also enables homotropic allosteric interactions between subunits, for example, in membrane protein αβ TCR [7] and L-Lactate dehydrogenase [8]. Such allosteric regulation was found to be the most common in oligomers with dihedral symmetries, especially in metabolic enzymes [9]. Yet another example are the death domains of several proteins involved in cell death and immune cell signaling where dimerization often leads to protein activation. Here, dimerization is if often mediated via domain swapping where two subunits exchange their parts to form an intertwined dimer [10]. The same principle can also apply to higher-order homo-oligomers, an example is the barnase domain-swapped trimer [11], and is also frequently associated with formation of protein aggregates/deposits [12].

As these advantages are almost intuitive, it is often assumed they should also provide a clear evolutionary benefit. However, Lynch suggested that homo-oligomers could have arisen from stochastic, non-adaptive processes [13][14] and that the benefits of homo-oligomerization are not all-pervasive, but rather dependent on the context and the properties of the individual protein [15]. These and other possible reasons as to why homo-oligomerization is such a frequently encountered property were also extensively discussed elsewhere [16][17][18][19][20].

2. Most Protein Homo-Oligomers Are Symmetric

Symmetry is an inherent property of almost all homo-oligomers characterized up to date. Although homo-oligomers often exhibit at least some degree of local asymmetry [17], this asymmetry is limited to small differences in the backbone position, differences in sidechain orientations or limited to a certain part of the protein, while the complex as a whole is still symmetric (Figure 1A). Local asymmetry may provide an insight into the mechanism of complex formation [21]. For example, in the case of domain swapped oligomers, local asymmetry may reveal the location of the hinge regions that connect the swapped portions of the subunits [22], as in the case of pancreatic ribonuclease where N-terminal regions are exchanged (Figure 1A). For a comprehensive review on structural asymmetry in homo-dimers, the reader is referred to the paper written by Swapna, Srikeerthana and Srinivasan [23].

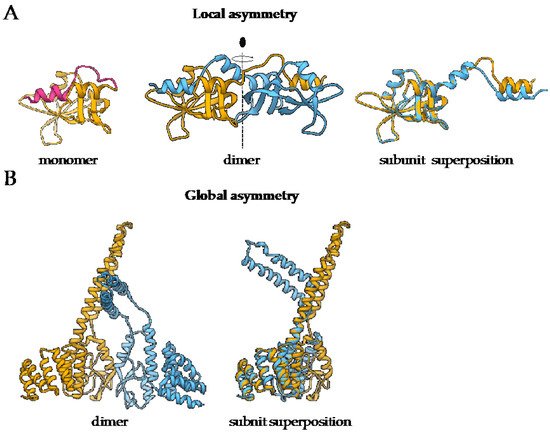
Ijms 22 09081 g001 550

Figure 1. The difference between local and global asymmetry. (A) An example of a globally symmetric homo-oligomeric complex with a substantial local asymmetry is the structure of bovine pancreatic ribonuclease N-term-swapped dimer (PDB: 1A2W) [23][24]. During the dimer formation, the N-terminal region of the monomer (PDB: 1A5P, pink) [25] is swapped the juxtaposed subunit. (B) Murine CHIP-U-box E3 ubiquitin ligase (PDB: 2C2L) [26] is an example of a globally asymmetric homo-oligomeric complex. Individual subunits are depicted in yellow and blue. For both complexes, the superposition of polypeptide chains is also presented to demonstrate the extent of structural differences between the subunits.

On the other hand, global asymmetry (Figure 1B) is rare. In the dataset of annotated biological assemblies (QSbio) [27], less than 5% of homo-oligomeric structures do not have symmetry (Figure 2A). The most observed symmetry types are cyclic symmetries (Cn in Schönflies notation) with a single axis of rotation, and dihedral symmetries (Dn) with at least one additional axis of rotation, perpendicular to the first one (Figure 2B). Cubic symmetry with the tetrahedral, octahedral and icosahedral arrangement is much less common; together, they account for roughly 1% of all structures. Icosahedral symmetry is often observed in viral envelopes, but there, the envelope is usually composed of several different polypeptide chains [28]. Interestingly, symmetries with an odd number of subunits are less common than those with an even number of subunits. This can be explained by the nature of interactions between subunits, which can be isologous or heterologous. Isologous interactions take place between identical surfaces and amino-acid residues on the interacting subunits, while, in heterologous interactions, different regions on juxtaposed subunits are involved (Figure 2C). Several studies have shown that isologous interactions are more favorable than heterologous [29][30][31][32], thus explaining the higher number of oligomers with an even number of subunits [16]. While C2 symmetric dimers are by far the most populous oligomeric state, dihedral symmetries prevail among homo-oligomers with a higher number of subunits. These can also be explained by the advantages of isologous interactions over heterologous, as interactions in cyclic homo-oligomers with more than two subunits are, by definition, heterologous. Symmetry is also related to a finite control of protein assembly by producing a closed set of subunits. On the contrary, aggregation of proteins through the non-finite assembly is related to several pathological conditions [33].

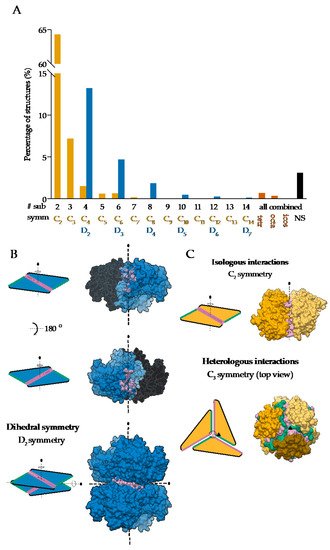
Ijms 22 09081 g002 550

Figure 2. Symmetries observed in the determined structures of homo-oligomeric protein complexes: (A) Relative distribution of symmetry types in QSbio with a 90% sequence similarity cutoff. Complexes were classified by the number of subunits (# sub) and the symmetry type (symm). Data for tetrahedral (tetr), octahedral (octa), icosahedral (icos) and non-symmetric (NS) complexes are combined for all number of subunits. (B) Assembly of a dihedral symmetry from parts of protein complexes with cyclic symmetry, glucose-6-phosphate 1-dehydrogenase (PDB: 6D23) [34]. In the representation of protein surfaces of the C2 symmetric subcomplexes, one of the subunits is transparent to enable visualization of the interaction surface. (C) Representation of the isologous and heterologous interactions in complexes with odd and even number of subunits in the case of orange carotenoid-binding protein (PDB: 5UI2) [35] and corrinoid adenosyltransferase (PDB: 2R6T) [36], respectively. Individual subunits are depicted with different shades of yellow. Distinct interaction surfaces are depicted with green and pink, respectively. Two- and three-fold axes are denoted by corresponding symbols.

References

  1. Stossel, T.P. From signal to pseudopod. How cells control cytoplasmic actin assembly. J. Biol. Chem. 1989, 264, 18261–18264.
  2. Mitchison, T.; Kirschner, M. Dynamic instability of microtubule growth. Nature 1984, 312, 237–242.
  3. Renatus, M.; Stennicke, H.R.; Scott, F.L.; Liddington, R.C.; Salvesen, G.S. Dimer formation drives the activation of the cell death protease caspase 9. Proc. Natl. Acad. Sci. USA 2001, 98, 14250–14255.
  4. Yu, X.; Sharma, K.D.; Takahashi, T.; Iwamoto, R.; Mekada, E. Ligand-independent dimer formation of epidermal growth factor receptor (EGFR) is a step separable from ligand-induced EGFR signaling. Mol. Biol. Cell 2002, 13, 2547–2557.
  5. Jiang, G.; den Hertog, J.; Hunter, T. Receptor-like protein tyrosine phosphatase alpha homodimerizes on the cell surface. Mol. Cell. Biol. 2000, 20, 5917–5929.
  6. Navia, M.A.; Fitzgerald, P.M.; McKeever, B.M.; Leu, C.T.; Heimbach, J.C.; Herber, W.K.; Sigal, I.S.; Darke, P.L.; Springer, J.P. Three-dimensional structure of aspartyl protease from human immunodeficiency virus HIV-1. Nature 1989, 337, 615–620.
  7. Schamel, W.W.A.; Alarcon, B.; Höfer, T.; Minguet, S. The Allostery Model of TCR Regulation. J. Immunol. 2017, 198, 47–52.
  8. Fushinobu, S.; Ohta, T.; Matsuzawa, H. Homotropic Activation via the Subunit Interaction and Allosteric Symmetry Revealed on Analysis of Hybrid Enzymes ofl-Lactate Dehydrogenase *. J. Biol. Chem. 1998, 273, 2971–2976.
  9. Bergendahl, L.T.; Marsh, J.A. Functional determinants of protein assembly into homomeric complexes. Sci. Rep. 2017, 7, 4932.
  10. Park, H.H. Domain swapping of death domain superfamily: Alternative strategy for dimerization. Int. J. Biol. Macromol. 2019, 138, 565–572.
  11. Zegers, I.; Deswarte, J.; Wyns, L. Trimeric domain-swapped barnase. Proc. Natl. Acad. Sci. USA 1999, 96, 818–822.
  12. Bennett, M.J.; Sawaya, M.R.; Eisenberg, D. Deposition diseases and 3D domain swapping. Structure 2006, 14, 811–824.
  13. Lynch, M. The evolution of multimeric protein assemblages. Mol. Biol. Evol. 2012, 29, 1353–1366.
  14. Lynch, M. Evolutionary diversification of the multimeric states of proteins. Proc. Natl. Acad. Sci. USA 2013, 110, E2821–E2828.
  15. Hagner, K.; Setayeshgar, S.; Lynch, M. Stochastic protein multimerization, activity, and fitness. Phys. Rev. E 2018, 98, 062401.
  16. Levy, E.D.; Teichmann, S. Structural, evolutionary, and assembly principles of protein oligomerization. Prog. Mol. Biol. Transl. Sci. 2013, 117, 25–51.
  17. Goodsell, D.S.; Olson, A.J. Structural symmetry and protein function. Annu. Rev. Biophys. Biomol. Struct. 2000, 29, 105–153.
  18. Ali, M.H.; Imperiali, B. Protein oligomerization: How and why. Bioorg. Med. Chem. 2005, 13, 5013–5020.
  19. Perica, T.; Marsh, J.A.; Sousa, F.L.; Natan, E.; Colwell, L.J.; Ahnert, S.E.; Teichmann, S.A. The emergence of protein complexes: Quaternary structure, dynamics and allostery. Colworth Medal Lecture. Biochem. Soc. Trans. 2012, 40, 475–491.
  20. Griffin, M.D.W.; Gerrard, J.A. The relationship between oligomeric state and protein function. Adv. Exp. Med. Biol. 2012, 747, 74–90.
  21. Bonjack, M.; Avnir, D. The near-symmetry of protein oligomers: NMR-derived structures. Sci. Rep. 2020, 10, 8367.
  22. Bonjack-Shterengartz, M.; Avnir, D. The enigma of the near-symmetry of proteins: Domain swapping. PLoS ONE 2017, 12, e0180030.
  23. Swapna, L.S.; Srikeerthana, K.; Srinivasan, N. Extent of structural asymmetry in homodimeric proteins: Prevalence and relevance. PLoS ONE 2012, 7, e36688.
  24. Liu, Y.; Hart, P.J.; Schlunegger, M.P.; Eisenberg, D. The crystal structure of a 3D domain-swapped dimer of RNase A at a 2.1-A resolution. Proc. Natl. Acad. Sci. USA 1998, 95, 3437–3442.
  25. Pearson, M.A.; Karplus, P.A.; Dodge, R.W.; Laity, J.H.; Scheraga, H.A. Crystal structures of two mutants that have implications for the folding of bovine pancreatic ribonuclease A. Protein Sci. 1998, 7, 1255–1258.
  26. Zhang, M.; Windheim, M.; Roe, S.M.; Peggie, M.; Cohen, P.; Prodromou, C.; Pearl, L.H. Chaperoned ubiquitylation—crystal structures of the CHIP U box E3 ubiquitin ligase and a CHIP-Ubc13-Uev1a complex. Mol. Cell 2005, 20, 525–538.
  27. Dey, S.; Ritchie, D.W.; Levy, E.D. PDB-wide identification of biological assemblies from conserved quaternary structure geometry. Nat. Methods 2017, 15, 67–72.
  28. Johnson, J.E.; Olson, A.J. Icosahedral virus structures and the protein data bank. J. Biol. Chem. 2021, 296, 100554.
  29. Lukatsky, D.B.; Zeldovich, K.B.; Shakhnovich, E.I. Statistically enhanced self-attraction of random patterns. Phys. Rev. Lett. 2006, 97, 178101.
  30. Lukatsky, D.B.; Shakhnovich, B.E.; Mintseris, J.; Shakhnovich, E.I. Structural similarity enhances interaction propensity of proteins. J. Mol. Biol. 2007, 365, 1596–1606.
  31. André, I.; Strauss, C.E.M.; Kaplan, D.B.; Bradley, P.; Baker, D. Emergence of symmetry in homooligomeric biological assemblies. Proc. Natl. Acad. Sci. USA 2008, 105, 16148–16152.
  32. Schulz, G.E. The dominance of symmetry in the evolution of homo-oligomeric proteins. J. Mol. Biol. 2010, 395, 834–843.
  33. Chiti, F.; Dobson, C.M. Amyloid formation by globular proteins under native conditions. Nat. Chem. Biol. 2009, 5, 15–22.
  34. Ortíz, C.; Botti, H.; Buschiazzo, A.; Comini, M.A. Glucose-6-phosphate dehydrogenase from the human pathogen Trypanosoma cruzi evolved unique structural features to support efficient product formation. J. Mol. Biol. 2019, 431, 2143–2162.
  35. Kerfeld, C.A.; Sawaya, M.R.; Brahmandam, V.; Cascio, D.; Ho, K.K.; Trevithick-Sutton, C.C.; Krogmann, D.W.; Yeates, T.O. The crystal structure of a cyanobacterial water-soluble carotenoid binding protein. Structure 2003, 11, 55–65.
  36. Mera, P.E.; St Maurice, M.; Rayment, I.; Escalante-Semerena, J.C. Structural and functional analyses of the human-type corrinoid adenosyltransferase (PduO) from Lactobacillus reuteri. Biochemistry 2007, 46, 13829–13836.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Biochemistry & Molecular Biology
Contributor MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Aljaž Gaber
View Times: 2.1K
Revisions: 2 times (View History)
Update Date: 23 Sep 2021
Table of Contents
    1000/1000
    Hot Most Recent
    ScholarVision Creations
    Feedback