
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Ronald Marquez | + 7175 word(s) | 7175 | 2021-08-17 05:36:12 | | | |
| 2 | Ronald Marquez | + 64 word(s) | 7239 | 2021-08-28 11:08:02 | | | | |
| 3 | Ronald Marquez | + 64 word(s) | 7239 | 2021-08-28 11:09:17 | | | | |
| 4 | Ronald Marquez | + 64 word(s) | 7239 | 2021-08-28 11:10:02 | | | | |
| 5 | Ronald Marquez | + 7 word(s) | 7182 | 2021-08-28 11:11:49 | | | | |
| 6 | Ronald Marquez | -1 word(s) | 7174 | 2021-08-28 17:20:25 | | | | |
| 7 | Ronald Marquez | Meta information modification | 7174 | 2021-08-28 17:29:47 | | | | |
| 8 | Ronald Marquez | + 2 word(s) | 7176 | 2021-08-28 17:32:16 | | | | |
| 9 | Ronald Marquez | + 4 word(s) | 7178 | 2021-08-28 17:35:33 | | | | |
| 10 | Ronald Marquez | -127 word(s) | 7051 | 2021-08-29 02:26:42 | | | | |
| 11 | Ronald Marquez | -128 word(s) | 7050 | 2021-08-29 02:32:07 | | | | |
| 12 | Ronald Marquez | -128 word(s) | 7050 | 2021-08-29 02:37:06 | | | | |
| 13 | Ronald Marquez | -128 word(s) | 7050 | 2021-08-29 03:39:18 | | | | |
| 14 | Ronald Marquez | -128 word(s) | 7050 | 2021-08-29 05:30:09 | | | | |
| 15 | Ronald Marquez | -126 word(s) | 7052 | 2021-08-29 06:02:33 | | | | |
| 16 | Rita Xu | -1377 word(s) | 5675 | 2021-08-31 05:39:39 | | | | |
| 17 | Ronald Marquez | + 116 word(s) | 5791 | 2021-08-31 07:16:20 | | | | |
| 18 | Ronald Marquez | + 129 word(s) | 5804 | 2021-08-31 07:21:58 | | | | |
| 19 | Rita Xu | + 129 word(s) | 5804 | 2021-08-31 07:34:38 | | | | |
| 20 | Ronald Marquez | + 245 word(s) | 6049 | 2021-08-31 07:39:11 | | | | |
| 21 | Rita Xu | + 245 word(s) | 6049 | 2021-08-31 07:41:50 | | | | |
| 22 | Ronald Marquez | Meta information modification | 6049 | 2021-08-31 09:00:23 | | | | |
| 23 | Ronald Marquez | Meta information modification | 6049 | 2021-08-31 16:58:13 | | | | |
| 24 | Ronald Marquez | Meta information modification | 6049 | 2021-09-01 02:06:57 | | | | |
| 25 | Ronald Marquez | Meta information modification | 6049 | 2021-09-01 02:10:01 | | | | |
| 26 | Ronald Marquez | Meta information modification | 6049 | 2021-09-05 20:38:29 | | | | |
| 27 | Ronald Marquez | -4517 word(s) | 1532 | 2024-09-08 08:58:38 | | | | |
| 28 | Ronald Marquez | -7 word(s) | 1525 | 2024-09-08 09:01:02 | | |
Video Upload Options
The oscillatory spinning drop method has been proven recently to be an accurate technique to measure dilational interfacial rheological properties. It is the only available equipment for measuring dilational moduli in low interfacial tension systems, as is the case in applications dealing with surfactant-oil-water three-phase behavior like enhanced oil recovery, crude oil dehydration, or extreme microemulsion solubilization. Different systems can be studied with this method with the lower density phase as the spinning drop, i.e, oil-in-water, microemulsion-in-water, oil-in-microemulsion, including systems with the presence of complex natural surfactants like asphaltene aggregates or particles. The technique allows studying the characteristics and properties of water/oil interfaces, particularly when the oil contains asphaltenes and when surfactants are present. We have found that using the oscillating spinning drop method to measure interfacial rheology properties can help make precise measurements in a reasonable amount of time. This is of significance when systems with long equilibration times, e.g., asphaltene or high molecular weight surfactant-containing systems are measured, or with systems formulated with a demulsifier which is generally associated with optimum formulation and a low interfacial tension.
1. The Oscillatory Spinning Drop Apparatus
The oscillatory spinning drop equipment was built a decade ago in the FIRP laboratory with the collaboration of the CITEC-ULA workshop, based on the oscillatory deformation of a spinning drop [21]. This apparatus can be used to perform interfacial rheology measurements of both low and ultralow interfacial tensions (as low as 10−4 mN/m). This is critical when the formulation is at or close to optimum [27][28][31], such as enhanced oil recovery or crude dehydration applications [29][30]. Dataphysics has available an oscillating spinning drop equipment, nevertheless, there are no reports of works with low or ultralow interfacial tensions with that type of model, therefore the innovative aspect of the apparatus described herein [21].
The current model, shown in Figure 1, includes a spinning capillary with a 4 mm internal diameter coupled to a motor and a transducer. The capillary rotates at a velocity, which is controlled by a PID unit. The drop area is changed by varying the rotational speed sinusoidally at frequencies between 0.015 and 0.25 Hz. The device automatically takes pictures at desired time intervals (down to 0.05 s). Each image allows determining the droplet diameter, which is automatically recorded together with the rotational velocity. Then, the droplet diameter and the rotational velocity are used to calculate the interfacial tension from the simplified Vonnegut equation [21].
Figure 1. Oscillating spinning drop interfacial rheometer recent version.
1.1. Basic Aspects of the Oscillatory Spinning Drop Interfacial Rheology Technique
The spinning drop tensiometer with an oscillating rotation velocity is used to measure interfacial compression rheology properties whose principle was proposed 40 years ago [32]. The description of our developed equipment was recently reported [21], and it was shown that the apparatus makes accurate and reliable measurements of interfacial rheology parameters at high, low, and ultralow interfacial tensions. The dilational modulus measured with the oscillatory spinning drop apparatus is the Young modulus (EYoung), which in two dimensions has compression and shear contributions, i.e., EYoung = E + G. Thus, it was recently reported that the measured elastic modulus E’ values are similar to those found with a pendant drop apparatus [21].
Some original interfacial rheological properties at and near optimum formulation (i.e., at hydrophilic-lipophilic deviation HLDN = 0, with ultralow interfacial tensions), were recently reported for the first time [28]. The systems studied range from low concentration (just above the critical microemulsion concentration cμc) to a large middle-phase microemulsion volume. It was systematically found that at HLDN = 0, very low values of the dilational moduli and interfacial viscosity are attained. This occurs probably because the diffusional mass transfer is very fast at optimum formulation [33]. Thus, the measurement at HLDN = 0 is an effective dilational (or compression) modulus, which considers the fast surfactant exchanges between the bulk and the interface in WIII systems [27]. This is particularly important because it explains the very deep minimum in emulsion stability at optimum formulation, and consequently, why it should be the selected formulation for enhanced oil recovery, crude oil dehydration, and desalting processes [34][35][36].
1.2. Practical Aspects of the Measurement
The oscillatory spinning drop technique requires specific conditions to ensure an accurate measurement; the droplet volume, the rotational speed, and the oscillation amplitude must be selected accordingly. Placing a suitable quantity of the internal phase droplet inside the external phase is tricky because, according to the interfacial tension value and the density difference between the fluids, a lower or higher volume droplet should be placed inside the capillary. The droplet aspect also depends on the rotational speed of the interfacial rheometer and of its oscillation range. A higher rotational speed elongates more the droplet, and if it happens, a lower drop volume must be inserted inside the capillary. The recommended drop volume varies from 10–30 µL for air-water or oil-water systems to 0.5–5 µL for ultralow tension systems. Table 1 indicates typical values for the drop volume, rotational speed and equilibration time. This rationale comes from the experience of thousands of measurements in our laboratory.
Table 1. Typical values of interfacial (or surface) tension, droplet volume, recommended rotational speed, and equilibration time for operation with the oscillatory spinning drop apparatus.
|
System |
Tension (mN/m) |
Droplet Volume (µL) |
Recommended Rotational Speed Interval (rpm) 1 |
Approximate Equilibration Time |
|
Surfactant-air-water |
10–40 |
20–25 |
7,000–10,000 |
30 min–a few hours |
|
Oil-water (with asphaltenes) |
10–40 |
20–25 |
7,000–10,000 |
1 h–several hours |
|
SOW with high tension |
2–10 |
10–20 |
6,000–10,000 |
20 min–2 h |
|
SOW system with low tension |
0.1–2 |
5–10 |
4,000–6,000 |
20 min–2 h |
|
SOW system with ultralow tension |
0.0001–0.1 |
0.5–5 |
3,000–4,000 |
1 min–1 h |
1 This is the recommended interval for rotational speeds according to the tension value and the area change [21].
After appropriate droplet volume, rotational speed and temperature are set, the next step is to input the oscillation rotational speed amplitude to carry out the measurement. The droplet’s interface (or surface) area variation must be no more than 10% to keep the rheological response linear [21]:. To achieve this, an oscillation amplitude from 300 to 1000 rpm is recommended when rotational speeds are between 3000–4000 rpm, 4000–6000 rpm or 6000–10,000 rpm for ultralow, low, and high interfacial tensions, respectively.
Finally, the oscillation frequency (ω) is adjusted according to the measurement that will be performed. For example, for systems where the interfacial rheological measurement will be related to emulsion stability, ω can be set at 0.1 Hz to match the characteristic time scale of the phenomenon [27]. In contrast, for a broader study of the system response to a frequency change, a frequency sweep can be performed from ω = 0.015 to 0.25 Hz.
When a frequency sweep is made with the oscillatory spinning drop interfacial rheometer, two levels of frequency could be analyzed [9][21]:
At a very low frequency (0.025 Hz or lower), the oscillation time is quite long; hence the time is sufficient for surfactant exchanges to occur and surfactants to adsorb. Therefore, surface concentration (i.e., surface tension) gradients are very low, relaxation occurs, and Gibbs-Marangoni effects are negligible. That is probably one of the reasons why dilational modulus becomes very low.
At a high frequency (much higher than 0.25 Hz), the oscillation time is very short. It doesn’t give sufficient time for surfactant molecules to adsorb when the droplet elongates. This generates an interface that behaves as an elastic body. The dilational modulus becomes very high, reaching the limiting elasticity plateau, where the interface behaves as an “insoluble” monolayer. Among the particularities of these systems, we can mention that the external phase must be transparent or just a little opaque; otherwise, the measurement cannot be performed because the software cannot distinguish the interface in the photographic data. Usually, experiments are carried out with a transparent external phase, so that the measurement is straightforward.
1.3. Measurements with the oscillating spinning drop in comparison with the pendant drop method
Pendant drop experiments with a KSV CAM 200 instrument and an air bubble in an SDBS solution have been performed to compare the accuracy of the oscillating spinning drop apparatus. The result with the pendant drop method was E’ = 3.4 ± 1.2 mN/m. The values of E’ are compatible with those measured with the spinning drop instrument of 3.6 ± 2.0 mN/m, although the phase angle and E'' were different. The measured E’ and E” are not intrinsic parameters and are affected by diffusion. They might also be affected by convection in the spinning drop instrument, due to the high rotation velocities, possibly explaining the higher measured dissipation. Nevertheless, experiments to determine its accuracy have been performed and reliable measurements were obtained [21].
In Figure 2 a typical measurement of dilational modulus E and elastic modulus E' performed with the oscillating spinning drop are shown. The system is comprised of heavy crude oil with high asphaltene content diluted in cyclohexane. The previously reported phenomenology with the pendant drop method is attained also with the spinning drop, showing a maximum in the elastic modulus, and then a decrease, when a 3D asphaltene film forms near 1,000 ppm asphaltene content [21].
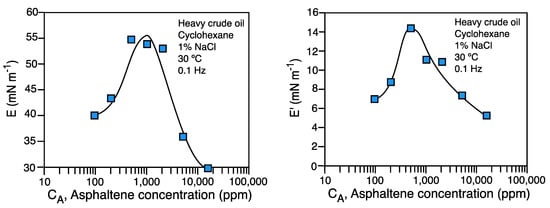
The spinning drop oscillating technique is the unique alternative of interfacial rheology study in applications where the emulsions must be as unstable as possible, e.g. for crude oil dehydrating or desalting, and low tension enhanced oil recovery.
References
- Drelich, J.; Fang, C.; White, C. Measurement of interfacial tension in Fluid-Fluid Systems. In Encyclopedia of Surface and Colloid Science; P. Somasundaran, Ed.; Marcel Dekker Inc, 2002; pp. 3152–3166.
- Salager, J.-L. Physico-chemical properties of surfactant-water-oil mixtures: phase behavior, micro-emulsion formation and interfacial tension, University of Texas at Austin TX, 1977.
- Loglio, G.; Pandolfini, P.; Liggieri, L.; Makievski, A. V.; Ravera, F. Determination of interfacial properties by the pendant drop tensiometry: Optimisation of experimental and calculation procedures. Bubble Drop Interfaces 2011, 2, 7–38, doi:10.1201/b12177-4.
- Salager, J.-L.; Manchego, L.; Márquez, L.; Bullón, J.; Forgiarini, A. Trends to attain a lower interfacial tension in a revisited pure alkyl polyethyleneglycol surfactant-alkane-water ternary system. basic concepts and straightforward guidelines for improving performance in enhanced oil recovery formulations. J. Surfactants Deterg. 2014, 17, 199–213, doi:10.1007/s11743-013-1534-5.
- Filippov, L.K. Dynamic surface tension of aqueous surfactant solutions. 2. diffusion-kinetic-convective controlled adsorption. J. Colloid Interface Sci. 1994, 164, 471–482, doi:10.1006/jcis.1994.1190
- Dukhin, A.; Goetz, P. Evolution of water-in-oil emulsion controlled by droplet-bulk ion exchange: Acoustic, electroacoustic, conductivity and image analysis. Colloids Surfaces A Physicochem. Eng. Asp. 2005, 253, 51–64, doi:10.1016/j.colsurfa.2004.10.125.
- Jeribi, M.; Almir-Assad, B.; Langevin, D.; Henaut, I.; Argillier, J.F. Adsorption kinetics of asphaltenes at liquid interfaces. J. Colloid Interface Sci. 2002, 256, 268–272, doi:10.1006/jcis.2002.8660.
- Fan, Y.; Simon, S.; Sjöblom, J. Interfacial shear rheology of asphaltenes at oil-water interface and its relation to emulsion stability: Influence of concentration, solvent aromaticity and nonionic surfactant. Colloids Surfaces A Physicochem. Eng. Asp. 2010, 366, 120–128, doi:10.1016/j.colsurfa.2010.05.034.
- Langevin, D. Rheology of adsorbed surfactant monolayers at fluid surfaces. Annu. Rev. Fluid Mech. 2014, 46, 47–65, doi:10.1146/annurev-fluid-010313-141403.
- Dukhin, S.S.; Kretzschmar, G.; Miller, R. Dynamics of Adsorption at Liquid Interfaces - Theory, Experiment, Application. Elsevier Sci. B. V. 1995, 1, 600.
- Edwards, D.A.; Brenner, H.; Wasan, D.T. Interfacial Transport Processes and Rheology; Butterworths-Heinemann, 1991; ISBN 0750691859.
- Van Voorst Vader, F.; Erkens, T.F.; Van Den Tempel, M. Measurement of dilatational surface properties. Trans. Faraday Soc. 1964, 60, 1170–1177, doi:10.1039/tf9646001170.
- Langevin, D. Dynamics of surfactant layers. Curr. Opin. Colloid Interface Sci. 1998, 3, 600–607, doi:10.1016/S1359-0294(98)80086-1.
- Buchavzov, N.; Ravera, F.; Hess, S.; Liu, Y.; Steinbrenner, U.; Stubenrauch, C. Interfacial tensions, partition coefficients, and interfacial elasticities: Measures for emulsion stability? Tenside, Surfactants, Deterg. 2007, 44, 230–238, doi:10.3139/113.100344.
- Reed, R.L.; Healy, R.N. Some physicochemical aspects of microemulsion flooding: a review. Improv. oil Recover. by surfactant Polym. flooding 1977, 383–437.
- Wade, W.; Morgan, J.C.; Schechter, R.S.; Jacobson, J.K.; Salager, J.-L. Interfacial tension and phase behavior of surfactant systems. Soc. Pet. Eng. J. 1978, 18, 242–252, doi:10.2118/6844-PA.
- Cayias, J.L.; Schechter, R.S.; Wade, W.H. Measurement of Low Interfacial Tension Via the Spinning Drop Technique. ACS Symp. Ser. 1975, 234–247, doi:10.1021/bk-1975-0008.ch017.
- Cayias, J.L.; Schechter, R.S.; Wade, W.H. Modeling crude oils for low interfacial tension. Soc. Pet. Eng. J. 1976, 16, 351–357, doi:doi.org/10.2118/5813-PA.
- Vonnegut, B. Rotating bubble method for the determination of surface and interfacial tensions. Rev. Sci. Instrum. 1942, 13, 6–9, doi:10.1063/1.1769937.
- Couper, A.; Newton, R.; Nunn, C. A simple derivation of Vonnegut’s equation for the determination of interfacial tension by the spinning drop technique. Colloid Polym. Sci. 1983, 261, 371–372, doi:10.1007/BF01413946.
- Zamora, J.M.; Marquez, R.; Forgiarini, A.M.; Langevin, D.; Salager, J.L. Interfacial rheology of low interfacial tension systems using a new oscillating spinning drop method. J. Colloid Interface Sci. 2018, 519, 27–37, doi:10.1016/j.jcis.2018.02.015.
- Cash, R.; Cayias, J.L.; Fournier, G.; McAllister, D.; Shares, T.; Schechter, R.S.; Wade, W.H. The Application Of Low Interfacial Tension Scaling Rules to Binary Hydrocarbon Mixtures. J. Colloid Interface Sci. 1977, 59, 39–44, doi:10.1016/0021-9797(77)90336-8.
- Chiwetelu, C.I.; Hornof, V.; Neale, G.H. The measurement of dynamic interfacial tension by photo-micropendography. J. Colloid Interface Sci. 1988, 125, 586–601, doi:10.1016/0021-9797(88)90025-2.
- Langevin, D. Emulsions, Microemulsions and Foams; Springer: Gewerbestr, Switzerland, 2020; ISBN 978-3-030-55681-5.
- Carbonaro, A.; Cipelletti, L.; Truzzolillo, D. Spinning Drop Dynamics in Miscible and Immiscible Environments. Langmuir 2019, 35, 11330–11339, doi:10.1021/acs.langmuir.9b02091.
- Derkach, S.R.; Krägel, J.; Miller, R. Methods of measuring rheological properties of interfacial layers (Experimental methods of 2D rheology). Colloid J. 2009, 71, 1–17.
- Marquez, R.; Forgiarini, A.M.; Langevin, D.; Salager, J.-L. Instability of Emulsions Made with Surfactant–Oil–Water Systems at Optimum Formulation with Ultralow Interfacial Tension. Langmuir 2018, 34, 9252–9263, doi:10.1021/acs.langmuir.8b01376.
- Marquez, R.; Forgiarini, A.M.; Fernández, J.; Langevin, D.; Salager, J.-L. New Interfacial Rheology Characteristics Measured using a Spinning-Drop Rheometer at the Optimum Formulation of a Simple Surfactant–Oil–Water System. J. Surfactants Deterg. 2018, 21, 611–623, doi:10.1002/jsde.12163.
- Marquez, R.; Forgiarini, A.; Langevin, D.; Salager, J.-L. Breaking of Water-In-Crude Oil Emulsions. Part 9. New Interfacial Rheology Characteristics Measured Using a Spinning Drop Rheometer at Optimum Formulation. Energy and Fuels 2019, 33, 8151–8164, doi:10.1021/acs.energyfuels.9b01476.
- Marquez, R.; Meza, L.; Alvarado, J.G.; Bullón, J.; Langevin, D.; Forgiarini, A.M.; Salager, J.-L. Interfacial Rheology Measured with a Spinning Drop Interfacial Rheometer: Particularities in More Realistic Surfactant–Oil–Water Systems Close to Optimum Formulation at HLDN = 0. J. Surfactants Deterg. 2021, 24, 587–601, doi:10.1002/jsde.12502.
- Marquez, R.; Antón, R.; Vejar, F.; Salager, J.L.; Forgiarini, A.M. New Interfacial Rheology Characteristics Measured Using a Spinning Drop Rheometer at the Optimum Formulation. Part 2. Surfactant–Oil–Water Systems with a High Volume of Middle-Phase Microemulsion. J. Surfactants Deterg. 2019, 22, 177–188, doi:10.1002/jsde.12245.
- Slattery, J.C.; Chen, J. Den; Thomas, C.P.; Fleming, P.D. Spinning drop interfacial viscometer. J. Colloid Interface Sci. 1980, 73, 483–499, doi:10.1016/0021-9797(80)90095-8.
- Fillous, L.; Cárdenas, A.; Rouvière, J.; Salager, J.-L. Interfacial Mass Transfer versus Formulation in Multiple Phase Anionic Surfactant-Oil-Water Systems. J. Surfactants Deterg. 1999, 2, 303–307, doi:10.1007/s11743-999-0081-8.
- Salager, J.-L.; Forgiarini, A.M.; Bullón, J. How to attain ultralow interfacial tension and three-phase behavior with surfactant formulation for enhanced oil recovery: A review. Part 1. Optimum formulation for simple surfactant-oil-water ternary systems. J. Surfactants Deterg. 2013, 16, 449–472, doi:10.1007/s11743-013-1470-4.
- Salager, J.-L.; Forgiarini, A.M.; Márquez, L.; Manchego, L.; Bullón, J.; Marquez, L.; Manchego, L.; Bullon, J. How to Attain an Ultralow Interfacial Tension and a Three-Phase Behavior with a Surfactant Formulation for Enhanced Oil Recovery: A Review. Part 2. Performance Improvement Trends from Winsor’s Premise to Currently Proposed Inter- and Intra-Molecular Mixtu. J. Surfactants Deterg. 2013, 16, 631–663, doi:10.1007/s11743-013-1485-x.
- Salager, J.-L. Fundamental basis for the action of a chemical dehydrant. Influence of the physical and chemical formulation on the stability of an emulsion. Int. Chem. Eng. 1990, 30, 103–116.
- Mannheimer, R.J.; Schechter, R.S. An improved apparatus and analysis for surface rheological measurements. J. Colloid Interface Sci. 1970, 32, 195–211, doi:10.1016/0021-9797(70)90044-5.
- Mannheimer, R.J.; Schechter, R.S. The theory of interfacial viscoelastic measurement by the viscous-traction method. J. Colloid Interface Sci. 1970, 32, 225–241, doi:10.1016/0021-9797(70)90046-9.
- Soo-Gun, O.H.; Slattery, J.C. Disk and biconical interfacial viscometers. J. Colloid Interface Sci. 1978, 67, 516–525, doi:https://doi.org/10.1016/0021-9797(78)90242-4.
- Krägel, J.; Siegel, S.; Miller, R.; Born, M.; Schano, K.H. Measurement of interfacial shear rheological properties: An apparatus. Colloids Surfaces A Physicochem. Eng. Asp. 1994, 91, 169–180, doi:10.1016/0927-7757(94)02901-6.
- Vandebril, S.; Franck, A.; Fuller, G.G.; Moldenaers, P.; Vermant, J. A double wall-ring geometry for interfacial shear rheometry. Rheol. Acta 2010, 49, 131–144, doi:10.1007/s00397-009-0407-3.
- Lucassen, J.; Hansen, R.S. Damping of waves on monolayer-covered surfaces. I. Systems with Negligible Surface Dilational Viscosity. J. Colloid Interface Sci. 1966, 22, 32–44, doi:10.1016/0021-9797(66)90064-6.
- Lucassen, J.; Van Den Tempel, M. Longitudinal waves on visco-elastic surfaces. J. Colloid Interface Sci. 1972, 41, 491–498, doi:10.1016/0021-9797(72)90373-6.
- Benjamins, J.; Cagna, A.; Lucassen-Reynders, E.H. Viscoelastic properties of triacylglycerol/water interfaces covered by proteins. Colloids Surfaces A Physicochem. Eng. Asp. 1996, 114, 245–254, doi:https://doi.org/10.1016/0927-7757(96)03533-9.
- Liggieri, L.; Attolini, V.; Ferrari, M.; Ravera, F. Measurement of the surface dilational viscoelasticity of adsorbed layers with a capillary pressure tensiometer. J. Colloid Interface Sci. 2002, 255, 225–235, doi:10.1006/jcis.2002.8665.
- Miller, R.; Liggieri, L. Progress in Colloid and Interface Science: Interfacial Rheology. 2009, 1, 699.
- Maru, H.C.; Wasan, D.T. Dilational viscoelastic properties of fluid interfaces-II. Experimental study. Chem. Eng. Sci. 1979, 34, 1295–1307, doi:10.1016/0009-2509(79)80021-4.
- Erni, P. Deformation modes of complex fluid interfaces. Soft Matter 2011, 7, 7586–7600, doi:10.1039/c1sm05263b.
- Scriven, L.E.; Sternling, C. V The Marangoni Effects. Nature 1960, 187, 186–188, doi:10.1038/187186a0.
- Lucassen, J.; Van Den Tempel, M. Dynamic measurements of dilational properties of a liquid interface. Chem. Eng. Sci. 1972, 27, 1283–1291, doi:10.1016/0009-2509(72)80104-0.
- Freer, E.; Svitova, T.; Radke, C.J. The role of Interfacial Rheology in reservoir mixed Wettability. J. Pet. Sci. Eng. 2003, 39, 137, doi:10.1016/S0920-4105(03)00045-7.
- Sonin, A.A.; Bonfillon, A.; Langevin, D. Role of Surface Elasticity in the Drainage of Soap Films. Phys. Rev. Lett. 1993, 71, 2342, doi:10.1103/PhysRevLett.71.2342.





