Production scheduling determines the most beneficial mining sequence over the life of mine. Developing a schedule that meets all mining aspects can substantially reduce mining costs and increase profitability. Among all underground mining methods, the sublevel caving (SLC) method is a common method with moderate development requirements, high production rate, and high degree of mechanization and flexibility. None of the manual planning methods and heuristic algorithms used in commercial software will lead to a truly optimal schedule. In sublevel caving, mathematical programming models, particularly mixed-integer programming, have been applied to provide an operationally feasible multi-time period's schedule. However, confined blasting conditions, chaotic material flow, and frequent mixing of ore and waste while loading broken ore at the drawpoint make sublevel caving method unique to produce a holistic plan.
1. Introduction
Despite the relatively lower fixed cost of the open-pit mining method, applying the open-pit mining method can be precluded due to geotechnical, operational, and environmental issues. The extraction of a high volume of overburden before ore extraction, high stripping ratio, pit wall failure, and reclamation cost are common challenges that considerably impact the feasibility of an open-pit mining method. In such cases, underground mining methods would be a good alternative
[1]. Underground mining methods such as sublevel caving (SLC), which can be applied in the hard rock mass, have become more popular because of their high potential production rates and low operating costs. Recent technological developments and improved solutions for designing, planning, and modeling SLC operations ramp up SLC application at greater depths in rock masses with more significant geotechnical challenges than ever before
[2].
As an underground mining method, SLC requires the investment of massive funds consisting of capital and operating costs. Thus, an integrated planning process through comprehensive studies to mitigate risks and maximize value is of the essence. Mine planning is considered a powerful tool to ensure the application of SLC. The implementation of operations research (OR) techniques in the mining industry dates back to the early 1960s
[1]. Since then, optimization techniques have been extensively applied to solve varied mine planning problems. Depending on how the problems are modeled, several techniques are available for solving mine production scheduling optimization. First, a model representing the system behavior is constructed using a scientific and mathematical approach. Then, different algorithms are used to solve the model and obtain the optimal solution. Musingwini
[3] categorizes OR models into five main groups: optimization models, simulation models, network models, multi-criteria decision-making models, and global optimization models. Optimization models use an exact algorithm to produce a single optimal solution for a maximization or minimization problem. Simulation models are mainly used to capture the uncertainty associated with the problem using an iterative approach that compares different scenarios. It does not necessarily generate an optimal solution, but it is helpful for risk analysis. A network model takes advantage of the graphical approach. The network model is a database model showing the relationships among the objects. The schema of a network model is a graphically aided algorithm including nodes and connecting links. In the network model, the objects are assumed as nodes and the relationships between the objects are depicted as arcs. They usually result in a single optimal solution. The multi-criteria cecision-making model is employed to make a decision that is subject to incorporating several criteria simultaneously. Finally, the global optimization model utilizes a heuristic algorithm to make an optimization problem more tractable without necessarily producing an optimal solution.
The production scheduling problem can be addressed by manual planning methods, heuristic algorithms, and exact algorithms. Exact algorithms are able to find an optimal solution by taking advantage of operation research techniques, but manual planning methods or heuristic algorithms will not lead to an optimal solution
[4]. Although heuristic algorithms can produce practical production schedules in a reasonable solution time, schedulers have no easy way to judge the quality of these schedules relative to the best schedule. In such cases, mathematical programming techniques can be used to produce optimal production schedules for underground mines
[5]. Mathematical programming models are formulated to generate an optimal mine extraction sequence while satisfying geotechnical, operational, environmental, and economic constraints
[6]. There is a direct link between tractability and the size of a model. This issue conducts a lot of research to develop a tractable and solvable model in a reasonable period of time.
2. Sublevel Caving Method
In recent years, surface and underground mass mining methods have experienced burgeoning interest as the mining sector is willing to exploit massive orebodies faster and more economically. Underground mining methods such as block-, panel- and sublevel-caving continue to be the top priority for deeply situated massive orebodies because of the high potential production rates and low operating costs. In addition, recent technological developments increase the application of caving operations on a larger scale, at greater depths, and in rock masses with greater geotechnical challenges
[2].
Originally, SLC was applied in the weak ground where collapse was more likely to happen due to the timber supports’ removal. Once each support was removed, the ore would cave and be mucked out to the perimeter drift. The next support would remain until the allowable dilution had been reached. The production rate was slow and resulted in poor ore recovery with high dilution. Later applications of SLC were used in relatively stronger ground with weak hanging walls to facilitate the caving process and avoid creating large voids. In this version of SLC, the ore did not cave anymore, and instead, the host rock above and immediately adjacent to the ore would cave. Strong ore led to the use of a drill-and-blast operation to extract the ore, which took the role of support removal. With the introduction of drill-and-blast, SLC could be utilized in orebodies with small footprints leading to natural cave development and also dipping geometry unfavorable for block caving. In recent times, the method has been applied to orebodies with strong hanging walls, where some techniques have been used to assist caving. Due largely to advances in drilling and blasting technologies, sublevels are conducted in 20 to 35 m vertical intervals, which are far higher than the traditional application of this method. The production drifts are drilled across the orebody in each level, and the haulage drift is developed to access the production drifts for ore transportation, services, and ventilation
[2].
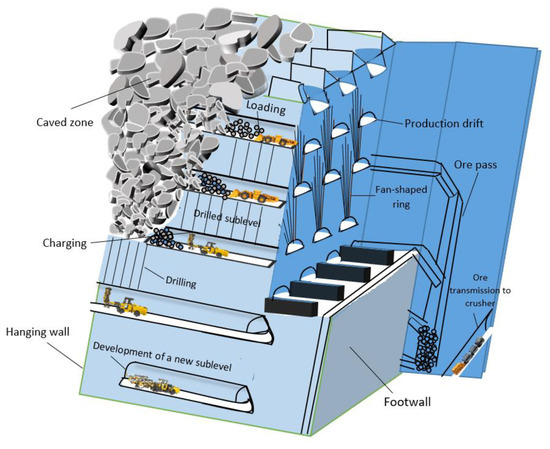
In an SLC mine, the orebody is divided into several vertical intervals through several horizontal openings called production drifts. A sublevel is known as the vertical interval formed between two production drifts on different levels
[7]. Subject to the mine layout (transverse or longitudinal), a perimeter drift is driven along or perpendicular to the strike of the orebody with a safe distance from the ore–waste contact. The perimeter drift is established to access the production drifts, ore transportation, services, and ventilation purposes
[2]. The major mining activities are divided into three groups: drifting and reinforcing; production drilling and blasting (ore fragmentation); and material handling, including ore drawing, loading, and transportation (see
Figure 1).
Figure 1. Schematic layout of SLC (Shekhar, 2020)
[8].
Mining operations start at the uppermost sublevel and proceed sequentially downwards. In each sublevel, the in-situ ore is drilled in a fan-shaped design along the production drift at a constant horizontal distance, called burden. Then, the ore is blasted, slice by slice, from the hanging wall to the footwall in a retreating manner
[7]. The restricted opening in the roof of production drift allows the blasted and caved materials to be flown under gravity, called a drawpoint. After finishing drill-and-blast operations, electric- or diesel-driven load-haul-dump (LHD) machines transport the broken ore from the drawpoints to the ore passes. A group of ore passes is positioned in certain spaces along the orebody strike. As more material is loaded, the void created at the drawpoint is filled by the fragmented material above the drawpoint. Thus, a void will be created around the blasted ring which exposes the hanging wall to the loss of support, resulting in the disintegration of rock at the ore and waste interface. The hanging wall starts to cave and fill the void
[9]. Depending on the regularity of the orebody, train systems or tuck haulages are utilized to transport ore from the ore passes to the crusher stations. After crushing, the ore is hoisted with a skip system to the surface (
Figure 1)
[10].
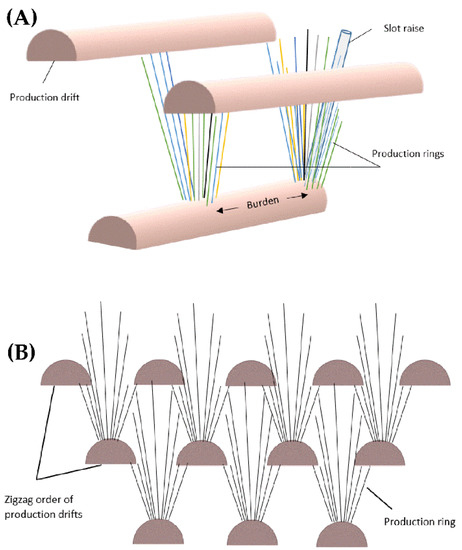
Once the production drifts have been excavated and reinforced, a slot drift on the far ore–waste contact or individual slot raise at the end of each production drift is placed to provide a free face for the first production ring. Minimizing the hole deviation when drilling is crucial because it will affect the fragmentation of the blasted ore and consequently the flow of the caving rock mass
[11]. To enable optimal coverage for drilling and to allow for the downward flow of caved material, production drifts are staggered in a zig-zag order between the levels
[10].
Figure 2 shows an upward production ring drilled in a fanned shape with a specific burden along with the production drifts orientation.
Figure 2. Schematic representation of drilling and blasting operation in an SLC mine. (
A) Fan-shaped design of production rings. (
B) Production drift pattern
[2].
Production management and draw strategy are imperative in SLC operations to accurately predict the ore and waste flow from the cave after production commences. The draw strategies and production management plans need to be variable and adaptable to the constantly changing operational situations in order to cope with unpredictable conditions such as the early inflow of waste, hang-ups, the arrival of large oversize material at drawpoints, and unscheduled equipment breakdowns and production incidents
[2]. As a result, developing a draw control strategy that simultaneously incorporates mine sequencing and material handling systems while minimizing mining costs and dilution objectives is a crucial step in the SLC mining method
[12]. An effective draw control strategy maximizes ore recovery while minimizing dilution or enables the system to delay dilution entry in the drawpoint by utilizing some countermeasures to stop dilution
[13].
3. Mathematical Programming Methods
Decision-making and finding the best choice are significant challenges that may greatly impact the success or failure of an operation. The most crucial issue is to formulate real-world problems in the form of mathematical programming models. The process of solving a real-world problem with a mathematical programming model consists of the following steps
[14]:
-
Step 1: identify and define the problem
-
Step 2: collect data and present the model
-
Step 3: solve the model
-
Step 4: validate the model
-
Step 5: provide results
In many real cases, the size of the model precludes planners from solving the scheduling problem simply. For example, in integer programming (IP), the size and solution time of the models are highly affected by the number of binary variables and the structure of constraints, which can make the model intractable. On the other hand, the key obstacle so far has been the complexity and uncertainty associated with real-life problems. Thus, carefully formulating the constraints and using heuristic algorithms copes with the tractability of mathematical models in scheduling problems.
A mathematical model specifies the mine sequence in the mining context to achieve a specific goal related to the mine production strategy while incorporating all geotechnical, operational, environmental, and marketing constraints
[15]. Deterministic scheduling models obtained by mathematical programming can generate an optimal solution exactly. However, their application is restricted by the large size of the problem making the model intractable. Furthermore, exact methods have their own limitations because models are a simplification of reality. Therefore, in many cases, production scheduling optimization problems do not perfectly match the exact algorithms, and heuristic approaches can be used to provide a procedure to reduce solution time
[3]. Thus, designing a model including a reasonable number of constraint and decision variables, especially binary variables, is high of importance. Therefore, applying some size reduction procedures such as heuristic algorithms prior to applying mathematical models is the best approach in many cases
[4].
4. Production Scheduling in Mines
Production scheduling specifies the extraction sequence, which can be different based on the mining method and the level of scheduling’s timeframe. In other words, production scheduling defines the tonnage and grades in each time period over the time horizon
[16]. An optimal schedule is expected to be sufficiently robust to reduce costs, increase equipment utilization, optimize recovery of marginal ores, and maintain production rates and product quality. Common strategic objectives in the industry are net present value (NPV) maximization, cost minimization, and reserve maximization. Relying only on manual planning methods or heuristic-based algorithms will generate non-optimal mine schedules
[17].
Depending on the precision and time horizon of the plan, a hierarchical process divides mine planning into strategic (long-term), tactical (medium-term), and operational (short-term) levels
[18]. Strategic scheduling indicates the maximum profitable envelope within the orebody, production sequences, and production rate. Tactical scheduling defines the annual mining sequence based on the production rate determined at the strategic level. Finally, operational scheduling must detail how operations in the near future will contribute to the achievement of the long-term plan
[1].
This exact approache, specifically, mixed-integer programming (MIP), has been widely used in production scheduling problems
[4]. However, the tractability of exact algorithms is detrimentally affected by its mathematical structure and moderately large size which makes it impossible to solve a production scheduling problem in a reasonable time
[6]. Optimization-based heuristic algorithms can be used, which incorporate the essential characteristics of the mining system while remaining mathematically tractable
[19]. In underground mining methods, the simulation-optimization approach is also applied to incorporate the uncertainty associated with mine operational parameters, such as velocities, capacities, maneuver times, failure times, and maintenance times, which are modeled using the probability density functions based on the historical data
[15]. Despite frequent intervention and the lack of a way to judge optimality, simulation and heuristics are able to handle non-linear problems as part of the scheduling procedure
[19].
5. Conclusions and Recommendations
SLC is a cost-effective method in large-scale operations with a high production rate, less upfront development, and maximum use of automated equipment. In a smaller-scale operation where the capacity benefits are less achievable, SLC can be utilized as a selective method with lower production rates. As with other underground mining methods, SLC requires a considerable amount of investment. In a real case, the deviation between the production schedule and mine operation can affect the continuity of mine operations. Thus, a production schedule that considers all sources of deviation should be improved and applied to underground mines, especially SLC.
Almost all research performed in the field of SLC has applied MIP to obtain an optimal production schedule. According to the mine strategies, proposed models focused on NPV maximization and deviation minimization between productions. They demanded quantities of ore while satisfying constraints including ore reserve, mine precedence, and integer variable restrictor, but none of them have considered any type of uncertainty, which is the inherent characteristic of SLC mine operations. As such, developing a mathematical model that can be reproduced in reality and enables the mine planner to establish and compare different mining scenarios to produce an optimal mining schedule is highly important.
In SLC operations, loading at the drawpoint is complex because of the confined blasting conditions, chaotic material flow, and continuous mixing of ore and waste above the drawpoint. The draw strategies and production schedules are the most important concerns which need to be adaptable to the constantly changing situations in an SLC mine. One of the challenges encountered by mine planners is considering different types of uncertainty, including operational, geological, and economic factors during the generation of long- and short-term mine production schedules. The schedule should consider in detail unpredictable operational conditions such as the early inflow of waste, hang-ups, arrival of oversized materials at drawpoints, and unscheduled equipment breakdowns and production incidents. Thus, developing a draw control strategy that incorporates sequencing and scheduling, production, and material handling systems that simultaneously minimizes mining costs and dilution objectives is a crucial step in SLC mining.
Geological factors such as the natural variability in orebody geometry and grade, ground conditions, and rock properties make each SLC project unique. Furthermore, economic factors such as variable ore prices and exchange rates also should be considered to provide a more realistic production plan. These uncertainties mean that effective risk management is required to be robust economically and technically to ensure that mine operations are feasible and profitable.