
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Huichen Jiang | + 215 word(s) | 215 | 2018-11-14 16:39:30 | | | |
| 2 | Huichen Jiang | + 1350 word(s) | 1350 | 2018-11-18 05:35:23 | | | | |
| 3 | Huichen Jiang | + 1351 word(s) | 1351 | 2018-11-20 14:49:55 | | | | |
| 4 | Huichen Jiang | + 1220 word(s) | 2571 | 2020-10-31 10:04:19 | | | | |
| 5 | Huichen Jiang | -1 word(s) | 2570 | 2020-10-31 10:13:27 | | | | |
| 6 | Huichen Jiang | + 6 word(s) | 2577 | 2020-10-31 10:17:03 | | | | |
| 7 | Peter Tang | -81 word(s) | 2496 | 2020-11-01 12:53:38 | | | | |
| 8 | Peter Tang | Meta information modification | 2496 | 2020-11-02 01:50:39 | | |
Video Upload Options
We collected data pertaining to Chinese listed commercial banks from 2008 to 2016 and found that the competition between banks is becoming increasingly fierce. Commercial banks have actively carried out diversification strategies for greater returns, and the financial reports show that profits are increasingly coming from the non-interest income benefits of diversification strategies. However, diversification comes with risk. We built a panel threshold model and investigated the effect of income diversification on a bank’s profitability and risk. Diversification was first measured by the Herfindahl–Hirschman index (HHI), and the results show that there is a nonlinear relationship between diversification and profitability or risk does exist. We introduced an interesting index based on the entropy to test the robustness of our model and found that a threshold effect exists in both our models, which is statistically significant. We believe the combination of the entropy index (ENTI) and the HHI enables more efficient study of the relationship between diversification and profitability or risk more efficiently. Bankers and their customers have increasingly been interested in income diversification, and they value risk as well. We suggest that banks of different sizes should adopt the corresponding diversification strategy to achieve sustainable development.
1. Introduction
1.1. Background
Since 2006, the reform of China's banking industry has taken a new and important step. The "Big Five" banks, the Bank of China Limited (BOC), Industrial and Commercial Bank of China Limited (ICBC), China Construction Bank Corp. (CCB), Agricultural Bank of China Limited (ABC), and Bank of Communications Co., Ltd. (BOCOM), have successfully completed shareholding system reform and are listed on the Chinese A-share stock market. At the same time, the reform of interest rate marketization (IRM) has been steadily promoted. Zhou Xiaochuan, China's central bank chief, pointed out that IRM enlarged the banks' pricing power and the pricing power on loans and deposits. Moreover, the reform will help the market play a role in allocating resources and reflect the independent pricing power of financial institutions on their products and services. In addition, customers can choose from similar financial products at different prices, so financial institutions will be able to provide a variety of financial products and services and offer different prices according to the customer's risk [1]. Additionally, in recent years, the Chinese government has emphasized the importance of promoting IRM reform in reports on the work of the government.
The outbreak of the global financial crisis in 2008 had a substantial and far-reaching impact on China's banking industry. Against the background of the global financial crisis, with the continuous reforms and innovations of China's financial system, interbank competition has intensified. According to our calculation, the net interest margin has been volatile over the years (see Figure 1), which means the traditional operating strategy based on interest income should be changed. Therefore, there is an urgent demand for Chinese commercial banks to transform and upgrade main businesses, and many banks have adopted the strategy of income diversification, by providing more abundant financial products and services (non-interest business) to broaden their income channels. As shown in Figure 2, non-interest income has increasingly contributed to operating income from 2008 to 2016.
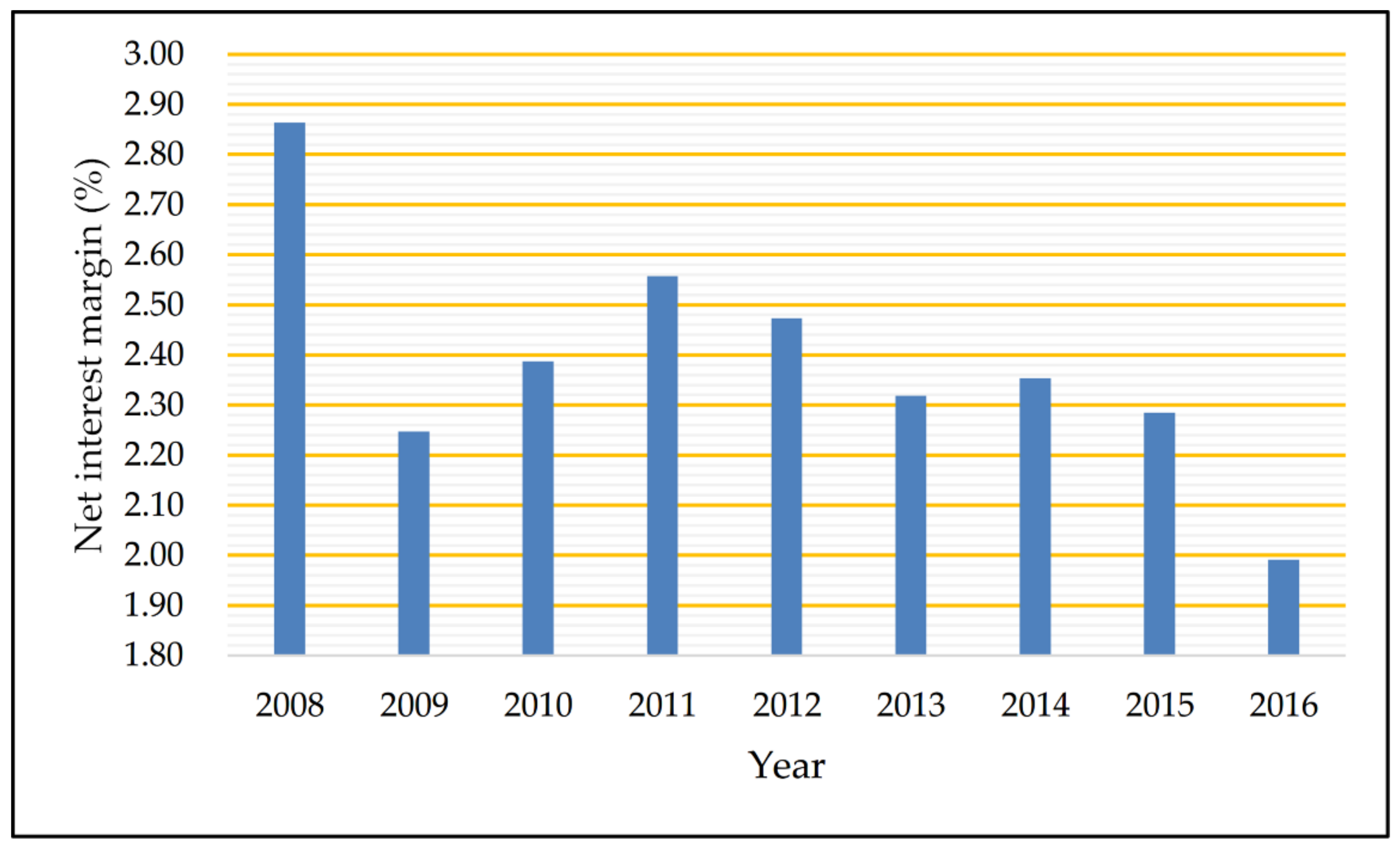
Figure 1. The net interest margin of listed commercial banks.
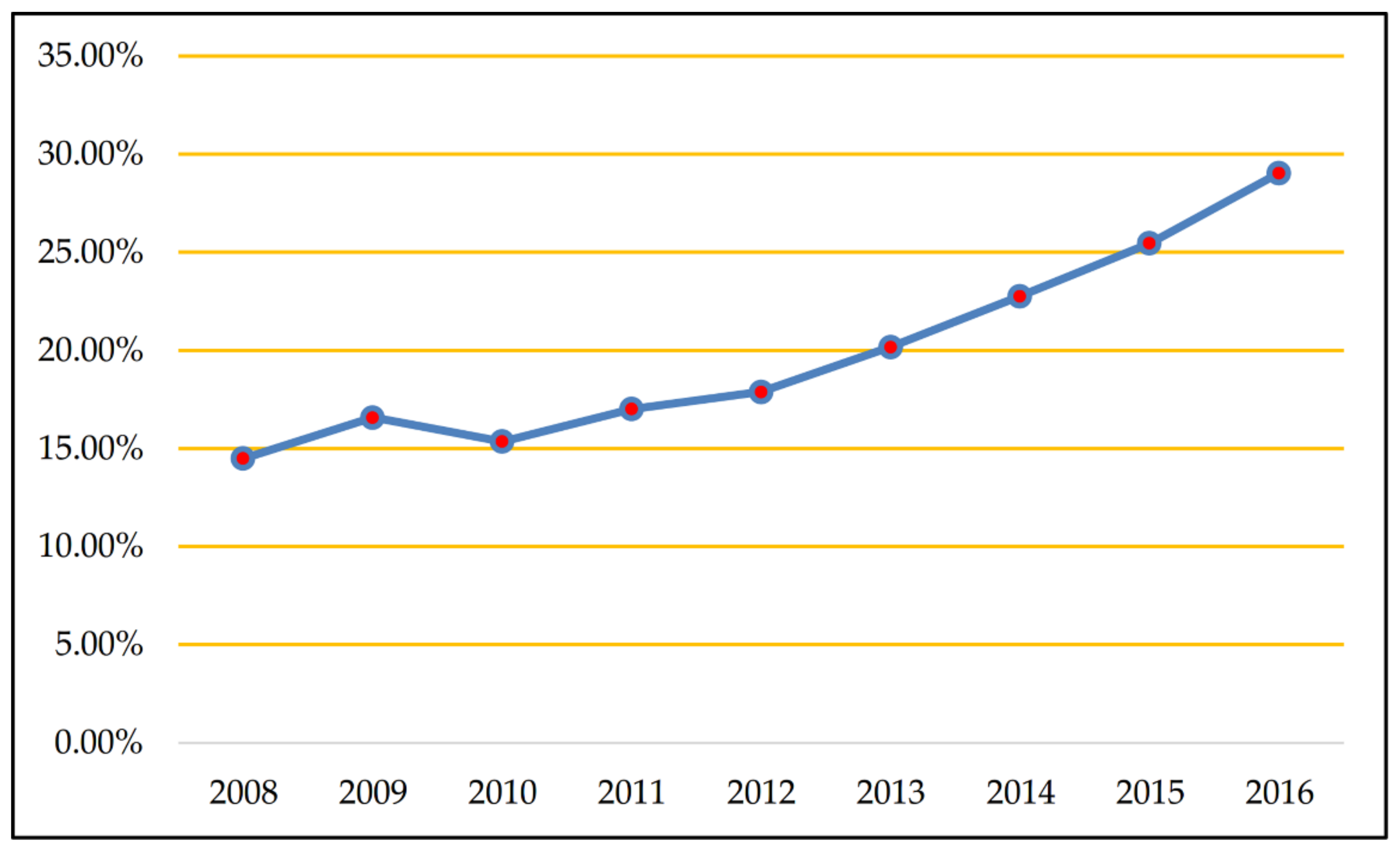
Figure 2. The percentage of non-interest income in operating income.
1.2. The Income Diversification of Banks
Income diversification has become an important trend in the development of modern banking. Most early studies were focused on the income diversification strategies of the European and American banking industries and described the potential benefits of income diversification from a variety of perspectives. First, by engaging in a wider range of financial activities, diversification can broaden revenue channels and cultivate new growth points. Second, banks can achieve operational synergies in providing a variety of financial products and services and enhance profitability with the economies of scale. In addition, since the non-interest business of a bank is irrelevant or not completely relevant to the interest business (which was believed to be more highly related to the economy), the diversification of income structures can reduce the volatility of the bank's income and stabilize it. Furthermore, by making full use of the customer information accumulated in traditional businesses, universal banks that adopt income diversification incur lower costs than specialized banks engaged only in traditional banking [2][3][4][5]. Moreover, some scholars believe that universal banks achieve well-diversified incomes and face lower risks than specialized banks. According to statistics from the Great Depression in the United States, most of the bankrupt banks were specialized, engaging only in a single business. To summarize, income diversification makes banks operate more efficiently by reducing cost, lowering risk, and enhancing profitability. Additionally, it can contribute to financial stability and economic development [6][7].
With the development of non-interest business all over the world, research can deepen our understanding of the effect of diversification on banks' profitability and risk. Studies have increasingly provided empirical evidence showing that diversification can benefit banks. Pennathur et al. [8] concluded that diversification benefited the public-sector banks of India by reducing default risk during the period 2001–2009. Shim [9] found that diversification reduced the likelihood of insolvency risk based on data of a USA bank holding company from 1992 to 2011, as the diversified income portfolio lowered the volatility of income. Other studies have found that income diversification may increase risk and reduce income and stability, theoretically and empirically. Lepetit et al. [10] found that there was a positive relationship between fee-based activities (commission income, which is a type of non-interest income) and solvency risk based on the data of European banks from 1996 to 2002. Hayden et al. [11] showed that, for most German banks, a higher level of diversification may result in a lower return, by using data of the loan portfolios of banks during the 1996–2002 period. Using data pertaining to banking in the USA from 1997 to 2002, Stiroh [12] analyzed the influence of income diversification on bank performance, and found that decreased interest income volatility contributed to income stability, while non-interest income was more volatile than interest income. Additionally, components of non-interest income, such as service charges and fees, are highly correlated with interest income. According to income structure statistics on the European banking industry from 1994 to 2002, Wang pointed out that, although the contribution of non-interest income to operating income increased significantly during the period, the growth of non-interest income to some extent compensated for the decline in interest income. However, the data show that, in 1995 and 1997, the rise in non-interest income was accompanied by a certain degree of increased operating costs. In other words, the impact of non-interest income on the profitability of banks is, on the whole, uncertain [13]. Additionally, Mercieca et al. [14] found that there was no direct diversification benefit for small European banks from 1997 to 2003, as they lacked experience and expertise on new types of business. Some researchers explored the heterogeneous effect of diversification, while some found that this effect does not exist. According to Baele et al., the diversification gains and costs are not significant for small and large banks in the European Union [15]. Hidayat et al. [16] studied the relationship between risk and diversification in Indonesian banks, and the results showed that the effect highly depends on the scale of the bank.
In sum, most research is currently focused on banks in the U.S. or in E.U. member countries, and the financial system and level of financial development in China are different from these countries. Therefore, whether or not income diversification is advantageous to Chinese banks is of great importance. In addition, there are no unanimous conclusions regarding the relationship between a bank's profitability and risk. Some people believe income diversification is beneficial for banks by improving profitability and income stability, while others argue that diversification may increase risk and income volatility. Moreover, it is worth noting that some research found that diversification may have a heterogeneous impact on banks. Therefore, we decided to use the panel threshold model to check whether the effects of diversification on profitability and risk are different among banks.
1.3. The Diversified Use of Entropy
Entropy is an interesting method, which was originally created and introduced in physics in the middle of the nineteenth century. It can be said that the entropy and its application formed the basis of statistical mechanics for understanding the conversion from heat to motive force. The idea of entropy is simple and easy to understand and has been developed by scientists and widely applied beyond the area of physics (see Scarfone [17], Martyushev and Seleznev [18], Tsallis and Souza [19], Pressé et al. [20]). According to Gulko [21], the first introduction of entropy in economic areas could date back to the 1960s. The entropy has been considered as a useful statistic and used in financial areas in the 1990s, Stutzer [22] and Avellaneda [23] made substantial and significant contributions to the application of entropy in finance.
Nowadays, the concept of entropy has been applied widespread in the areas of economic and financial studies.
The concept of entropy could be used in the pricing of financial products. By using the minimization of relative entropy, Stutzer [24] provided a simple way to derive the Black–Scholes option pricing model. Additionally, Kitamura et al. [25] pointed out that the entropy-based approach performs better than the traditional linear approach if non-normalities of observations exist. Inspired by Buchen et al. [26], Brody et al. [27], based on Rényi entropy, designed an entropic pricing method that required fewer parameters than the traditional approach.
The entropic method is also used in analyzing financial risk and financial crises. In the analysis of interbank contagion, the maximum entropy approach has become predominant [28]. Based on the concept of directional entropy, Bowden [29] enhanced a favored financial risk management tool called value at risk (VaR), which can measure tail risk. Pele et al. [30] proved that the entropy of the distribution function of intraday returns can predict classical measures of market risk, including the VaR, and had more informational content than the traditional ones. Yang and Qiu [31] believed that the introduction of entropy can contribute to decision-making. Based on Tsallis [32], Gençay and Gradojevic [33][34] introduced and developed an entropic approach as a measure of market expectations, and their further research [35] showed the application of Tsallis entropy and approximate entropy in finance to be a good predictor of the financial crises in 1987 and 2008. Boyarchenko [36] used relative entropy to measure the implied amount of ambiguity investors face, based on Hansen and Sargent [37].
Additionally, the entropy can be applied in financial time series analysis. Bekiros [38] designed a shift-invariant discrete wavelet transform (SIDWT), which uses the entropy-based criterion of obtaining the optimal depth of wavelet decomposition. The new methodology is superior to the traditional subjective approach and can be used in financial time series analysis. Dimpfl [39] discussed how transfer entropy can be applied to analyzing the information flows among financial markets. Compared with the Granger causality, Zaremba [40] pointed out that the transfer entropy can identity the nonlinear dependence better. Besides, Geman et al. [41] filled the gap of traditional financial literatures by analyzing the multi-dimensional density of the returns of assets with entropic framework.
As mentioned above, the aim of the research is to identity the impacts of income diversification on the return and risk of banks. Therefore, the measure of diversification is crucial for our research. As prior researches proved that, the Herfindahl–Hirschman Index (HHI) can be a good measure of diversification [42], while Tabak et al. [43] showed that entropic index can also be used as a measure of diversification. Therefore, we follow the traditional research and use the HHI to measure the diversification of banks and the entropy index (ENTI) is used for checking the robustness of our results.
2. Development
Our major contributions are as follows: First, we deepen prior research by analyzing the effect of income diversification on a bank's profitability and risk. Moreover, we study the effect of diversification on credit risk as measured by the non-performing loan ratio and insolvency risk as measured by the Z-score (the lower the Z-score is, the higher the bank's financial stability will be). Second, studies on the effect of income diversification have not come to unanimous conclusions; we built a panel threshold model for analyzing the effect of diversification. Diversification was first measured by the Herfindahl–Hirschman index (HHI), and the results show that there is a nonlinear relationship between diversification and profitability or risk. We introduced an interesting index based on entropy to test the robustness of our model and found that the threshold effect exists in both of our models, which is statistically significant. We believe that the combination of the entropy index (ENTI) and the HHI can be used to study the relationship between diversification and profitability or risk more efficiently. Bankers and their customers are becoming increasingly interested in income diversification, and they value risk as well. We suggest that banks of different sizes should adopt the corresponding diversification strategy to achieve sustainable development. In addition, we hope that the combination of ENTI and HHI can be widely used in further studies, and banks can control risk and earn more profit in the future.
3. Findings
By using the panel threshold model, we analyzed the relationship between income diversification and a bank's profitability and risk based on panel data of listed A-share commercial banks from 2008 to 2016. A summary and suggestions for the results are shown below.
According to the calculation in Section 3, we found that the threshold parameter of Model 1 is 10.33739 trillion RMB, which indicates that the size of the "Big Four" Chinese banks (ICBC, CCB, ABC, and BOC) exceeds the threshold parameter, and they are likely to earn more profit by diversification. The threshold parameter calculated for Model 2 is 8.403169 trillion RMB, which shows that the "Big Four" tend to realize a low level of credit risk with diversification. Additionally, the estimation of Model 3 shows a threshold parameter of 1.063901 trillion RMB, and there are 14 banks in the group whose size is greater than this parameter, while the sizes of two banks, NJCB and NBCB, are smaller, which means that, with increased diversification, their solvency risk as measured by Z-score will increase.
Based on the results, our suggestions are as follows: First, large banks tend to earn more profit and have less credit risk and solvency risk; this may be due to superior risk management techniques. Besides, large banks have a long history and thus have accumulated customer resources and formed brand recognition. Additionally, large banks are capital-abundant, while small banks lack the advantage in terms of customer relationships and capital. Meanwhile, there is room to develop diversification of small banks. With the development of Fin-Tech, artificial intelligence techniques such as Deep Learning, and the application of Big Data, the traditional business and non-interest income business of banks have been gradually influenced, so small banks may grow rapidly with diversification if they operate prudently and control risk efficiently. Second, diversification currently benefits large banks; however, if they do not prevent risk efficiently, risk will be system-wide and result in considerable costs. Therefore, regulators should strengthen the supervision of banks, for example, by the use of macro-prudential measures.
The entry is from 10.3390/e20040255
References
- Zhou, X.C. Some Thoughts Concerning the Promoting the Interest Rate Marketization. Available online: kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CCND&dbname=CCNDLAST2011&filename=JRSB201101050019 (accessed on 26 February 2018).
- Gallo, J.G.; Apilado, V.P.; Kolari, J.W. Commercial bank mutual fund activities. J. Bank. Financ. 1996, 20, 1775–1791.
- Ramasastri, A.S.; Samuel, A.; Gangadaran, S. Income Stability of Scheduled Commercial Banks. Econ. Polit. Weekly 2004, 39, 1311–1319.
- Chiorazzo, V.; Milani, C.; Salvini, F. Income diversification and bank performance. J. Financ. Ser. Res. 2008, 33, 181–203.
- Smith, R.; Staikouras, C.; Wood, G. Non-Interest Income and Total Income Stability. Available online: http://papers.ssrn.com/sol3/papers.cfm?abstract_id=530687 (accessed on 4 April 2018).
- Vennet, R.V. Cost and Profit Efficiency of Financial Conglomerates and Universal Banks in Europe. J. Money Credit Bank. 2002, 34, 254–282.
- Benston, G.J. Universal Banking. J. Econ. Perspect. 1994, 8, 121–143.
- Pennathur, A.K.; Subrahmanyam, V.; Vishwasrao, S. Income diversification and risk. J. Bank. Financ. 2012, 36, 2203–2215.
- Shim, J. Bank capital buffer and portfolio risk. J. Bank. Financ. 2013, 37, 761–772.
- Lepetit, L.; Nys, E.; Rous, P.; Tarazi, A. Bank income structure and risk. J. Bank. Financ. 2008, 32, 1452–1467. [Green Version]
- Hayden, E.; Porath, D.; Westernhagen, N.V. Does diversification improve the performance of German banks? J. Financ. Serv. Res. 2007, 32, 123–140.
- Stiroh, K.J.; Rumble, A. The dark side of diversification. J. Bank. Financ. 2006, 30, 2131–2161.
- Wang, Z.J. The Non-Interest Income of European Banking Sector. Stud. Int. Financ. 2004, 7, 47–52. (In Chinese)
- Mercieca, S.; Schaeck, K.; Wolfe, S. Small European banks: Benefits from diversification. J. Bank. Financ. 2007, 31, 1975–1998.
- Baele, L.; De Jonghe, O.; Vennet, R.V. Does the stock market value bank diversification? J. Bank. Financ. 2007, 31, 1999–2023.
- Hidayat, W.Y.; Kakinaka, M.; Miyamoto, H. Bank risk and non-interest income activities in the Indonesian banking industry. J. Asian Econ. 2012, 23, 335–343.
- Scarfone, A.M. Entropic forms and related algebras. Entropy 2013, 15, 624–649.
- Martyushev, L.M.; Seleznev, V.D. Maximum entropy production principle in physics, chemistry and biology. Phys. Rep. 2006, 426, 1–45.
- Tsallis, C.; Souza, A.M. Constructing a statistical mechanics for Beck-Cohen superstatistics. Phys. Rev. E 2003, 67, 026106. [PubMed]
- Pressé, S.; Ghosh, K.; Lee, J.; Dill, K.A. Principles of maximum entropy and maximum caliber in statistical physics. Rev. Mod. Phys. 2013, 85, 1115.
- Gulko, L. The entropy theory of stock option pricing. Int. J. Theor. Appl. Financ. 1999, 2, 331–355.
- Stutzer, M. A simple nonparametric approach to derivative security valuation. J. Financ. 1996, 51, 1633–1652.
- Avellaneda, M. Minimum-relative-entropy calibration of asset-pricing models. Int. J. Theor. Appl. Financ. 1998, 1, 447–472.
- Stutzer, M.J. Simple entropic derivation of a generalized Black-Scholes option pricing model. Entropy 2000, 2, 70–77.
- Kitamura, Y.; Stutzer, M. Connections between entropic and linear projections in asset pricing estimation. J. Econom. 2002, 107, 159–174.
- Buchen, P.W.; Kelly, M. The maximum entropy distribution of an asset inferred from option prices. J. Financ. Quant. Anal. 1996, 31, 143–159.
- Brody, D.C.; Buckley, I.R.; Constantinou, I.C. Option price calibration from Rényi entropy. Phys. Lett. A 2017, 366, 298–307.
- Liu, A.Q.; Paddrik, M.; Yang, S.Y.; Zhang, X.J. Interbank contagion: An agent-based model approach to endogenously formed networks. J. Bank. Financ. 2017, in press.
- Bowden, R.J. Directional entropy and tail uncertainty, with applications to financial hazard. Quant. Financ. 2011, 11, 437–446.
- Pele, D.T.; Lazar, E.; Dufour, A. Information entropy and measures of market risk. Entropy 2017, 19, 226.
- Yang, J.; Qiu, W. A measure of risk and a decision-making model based on expected utility and entropy. Eur. J. Oper. Res. 2005, 164, 792–799.
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487.
- Gradojevic, N.; Gencay, R. Overnight interest rates and aggregate market expectations. Econ. Lett. 2008, 100, 27–30.
- Gençay, R.; Gradojevic, N. Crash of ’87—Was it expected?: Aggregate market fears and long-range dependence. J. Empir. Financ. 2010, 17, 270–282.
- Gençay, R.; Gradojevic, N. The Tale of Two Financial Crises: An Entropic Perspective. Entropy 2017, 19, 244.
- Boyarchenko, N. Ambiguity shifts and the 2007–2008 financial crisis. J. Monet. Econ. 2012, 59, 493–507.
- Hansen, L.P.; Sargent, T.J. Recursive robust estimation and control without commitment. J. Econ. Theor. 2007, 136, 1–27.
- Bekiros, S.D. Timescale analysis with an entropy-based shift-invariant discrete wavelet transform. Comput. Econ. 2014, 44, 231–251.
- Dimpfl, T.; Peter, F.J. Using transfer entropy to measure information flows between financial markets. Stud. Nonlinear Dyn. Econom. 2013, 17, 85–102.
- Zaremba, A.; Aste, T. Measures of causality in complex datasets with application to financial data. Entropy 2014, 16, 2309–2349. [Green Version]
- Geman, D.; Geman, H.; Taleb, N.N. Tail risk constraints and maximum entropy. Entropy 2015, 17, 3724–3737.
- Brighi, P.; Venturelli, V. How functional and geographic diversification affect bank profitability during the crisis. Financ. Res. Lett. 2016, 16, 1–10.
- Tabak, B.M.; Fazio, D.M.; Cajueiro, D.O. The effects of loan portfolio concentration on Brazilian banks’ return and risk. J. Bank. Financ. 2011, 35, 3065–3076.




