
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Ekhard K. H. Salje | + 8346 word(s) | 8346 | 2021-05-08 07:51:57 | | | |
| 2 | Nora Tang | -2756 word(s) | 5590 | 2021-06-15 07:59:37 | | |
Video Upload Options
Ferroelastic twinning in minerals is a very common phenomenon. The twin laws follow simple symmetry rules and they are observed in minerals, like feldspar, palmierite, leucite, perovskite, and so forth. The major discovery over the last two decades was that the thin areas between the twins yield characteristic physical and chemical properties, but not the twins themselves. Research greatly focusses on these twin walls (or ‘twin boundaries’); therefore, because they possess different crystal structures and generate a large variety of ‘emerging’ properties. Research on wall properties has largely overshadowed research on twin domains.
1. Introduction
Twinning of minerals has intrigued mineralogists as long as mineralogy was established as a discipline by Haüy in 1797 [1]. At the beginning of the 20th century, many textbooks and research articles in mineralogy focused on twinning from a geometrical perspective [2][3][4][5][6][7][8]. Many of the early pioneers of mineralogy and crystallography were involved in this research, which highlights its importance. Landmark contributions came from Hugo Strunz [9] and Paul Ramdohr [10], who were inspirational for generations of mineralogists. The impact of work on the classification of ‘twins’ declined over recent decades; however, while research on the consequences of twinning sharply increased in a wider field outside mineralogy, namely physics, chemistry, ferroic materials, and nanotechnology. More than 8000 papers on twinning were published in 2020 alone. The fundamental shift came with a change of focus from twins to twin walls. A simple experiment partially initiated the new perspective, which was first disbelieved but then confirmed and extended to many other scenarios. The experimental discovery was that, in a specific tungstate mineral with perovskite structure, WO3, the boundary between various twins, the so-called ‘twin boundary’ or ‘twin wall’, has completely different physical properties from the twin domains (Figure 1). In this particular case, the twins are insulators while the twin boundaries are highly conducting at room temperature and become superconducting below ca. 3 K [11].

Figure 1. Topology (left), conductivity (middle), and piezoelectricity (right) of twin structures in WO3 at room temperature. The structure is tetragonal P-421m and piezoelectric [12]. Twin walls appear as borders between twin domains on the right, and as bright conducting regions in the middle panel. The piezoelectricity is short-circuited in the highly conducting domain walls, which now appear dark in the PFM image on the right (horizontal length of the image 1.5 µm, after [13]).
This review will describe other properties, and they were later identified to be localized in the twin walls, but not in the twin domains. These properties are highly relevant for technological applications and they triggered the shift from research on twin domains to research on domain walls. Hence, the fundamental new discovery is that twin walls are not simply thin layers inside minerals with essentially the same properties as the twin domains. Instead, they represent novel materials, confined to the twin walls, which do not exist as domains. Therefore, it is wrong to presume that the atomic configurations in the twin walls are the same as in the twins. This realization is similar to the earlier observation that surfaces are special because they contain surface reconstructions and surface relaxations, which often lead to the discovery of important new structures that are fundamentally different from the bulk. The earlier notion that twin walls are like internal surfaces, rather than infinitely thin layers of glue between twin domains, hence has found some late justification. The difference between twin boundaries and surfaces is that minerals can contain a large number of twin boundaries, while surface regions are necessarily limited under most circumstances. Hence, the emphasis of current research is to control twinning and use the twin walls as active elements. Applications are superconducting layers, transistors, photoelectric detectors, memory devices, piezoelectric layers, sources of chemical elements for reactions in confined spaces, and many more. The key notion is that wall properties are fundamentally different from the bulk properties. These physical, chemical, and structural properties are typically ‘emerging’, i.e., they exclusively relate to the features of the twin wall. They disappear when the twin walls disappear, so that mono-domain samples do not display any of these emerging properties.
The move towards research on specific micro- and nano-structures that largely started in 2010 with a new research discipline of ‘domain boundary engineering’ [14][15]. The aim was to understand how to generate twinned materials with desirable twin wall effects. A recent review by Nataf et al. [16][17] summarizes many aspects of successes and failures in ‘domain wall engineering’ from a physics perspective. From a mineralogical perspective, many of these effects were initially discovered in minerals with naturally occurring twin walls. We will now review some examples of minerals where important wall properties were found. We will then argue that much more work needs to be done on different twins in other minerals and highlight some open questions.
2. Ferroelastic Twin Laws in Minerals
Typical examples for phase transitions in minerals, which constitute large proportions of the earth’s crust, are those of quartz and feldspar. Quartz transforms from a high-temperature form with 622 symmetry (β-phase) via one or two incommensurate phases (INC) into the trigonal a phase with 32 symmetry (α-phase) [18]. The transition mechanism is related to the rotation of SiO4 tetrahedra with additional small distortions of the tetrahedral bond lengths and bond angles. The symmetry change during the phase transition is related to the appearance of a piezoelectric symmetry tensor, so that the transition cannot be ferroelastic. No ferroelastic twin laws are symmetry allowed to explain the multiple twin structures, because quartz is, instead, co-elastic. The inner structure of its twin walls in quartz has not yet been fully explored, and it still constitutes a major challenge to mineralogists [19][20]. For example, first principle DFT calculations are highly desirable for the determination of local crystal structures in twin walls of quartz. Co-elastic minerals are defined as undergoing strain deformations during phase transitions that are not confined to the symmetry breaking required for ferroelasticity. The strain often is a volume strain, like in the case of quartz, which does not lead to twinning, but allows twin-like structures inside the incommensurate phases. Nevertheless, co-elastic minerals are often twinned for other reasons than ferroelasticity, such as growth twinning, twinning under uniaxial stress, etc. Their twin boundaries are still awaiting a major research effort to understand their local structures.
This behavior contrasts with the structurally more intricate transitions in feldspars. Their transitions are related to three mechanisms: (i) the ordering of Al and Si in a tetrahedral network, (ii) structural distortions of the network of an essentially displacive nature (with a variety of critical points in the Brillouin zone), and (iii) the ordering/exsolution of the alkali and earth-alkali atoms. Na-feldspar is monoclinic C2/c at high temperatures and triclinic P-1 at low temperatures. The phase transition is related to the simultaneous symmetry breaking of the monoclinic structure via a displacive lattice distortion and a simultaneous ordering of the Al and Si atoms. At lower temperatures (around 950 K), the contributions of these two processes change in a crossover mechanism [21][22]. Two order parameters characterize the transition behavior. A weak thermodynamic singularity occurs due to a second-order transition with predominantly displacive character due to the tilt of the structural crankshafts. This lattice distortion drags with it a cation ordering process, which itself drives a crossover mechanism that operates without actual symmetry breaking at lower temperatures [23]. The coupling between several structural instabilities is very common in mineral systems and may, at first sight, seem to be rather complicated. Nevertheless, both of the mechanisms follow the same ferroelastic symmetry breaking process from the monoclinic to the triclinic phase. This means that the twin laws can be derived uniquely from symmetry conditions. The orientation of ferroelastic twins is then fully determined by the deformation of the P-1 phase relative to the C2/c phase. A full analysis of albite and pericline twin laws in alkali feldspars in [24] demonstrates the power of this method.
A complete description of all possible ferroelastic transition symmetries with many examples of minerals can be found in a textbook [25] and a specific review for the application of Landau theory in minerals [26]. A classification of symmetry conditions for the strain that determines twin laws was published by Carpenter and collaborators [27][28][29]. They derived a formal framework for detailed observations of the dynamical behavior of twin structures.
The orientation of ferroelastic twins is determined by the Sapriel conditions that twin walls are strain free [30]. Only two possible types of walls between twins are symmetry allowed. They are either completely fixed by the crystallography of the low symmetry phase or they are not. Fixed walls are called w-walls and flexible walls are called w’-walls. W-walls are related to mirror planes that are lost during the phase transition, while w’-walls contain equivalent diads inside the walls. The mineral palmierite is a typical example. Figure 2 shows the twin structure of a palmierite sample with composition Pb3(AsO4)2, which underwent a phase transition R-3m to C2/m. During the transition, the sample developed twins with w and w’ twin walls. The image shown in Figure 2 was taken along the pseudo-triad, which explains the almost threefold symmetry of the twin walls. The exact angles between the twin walls follow directly from the Sapriel condition and they deviate from the multiples of 90° and 30°. In 2020, Yokota et al. [31] found that all of the twin walls in palmierite are piezoelectric, while the twin domains are not. The structural symmetry inside the twin walls, namely m and 2, was confirmed.

Figure 2. Birefringence image of the twin structure of the palmierite Pb3(AsO4)2 in the C2/m phase. Twin variants appear as black and white regions. The birefringence image was taken along the pseudo-trigonal axis with some twin domains in extinction direction (after [32]).
W walls in Figure 2 appear as sharp lines because they are along the lost mirror plane of the R-3m phase which are perpendicular to the surface. W’ walls are inclined to the surface and change their orientation with temperature. They contain the broken diads of the high symmetry phase. The angles between the twin walls deviate from the multiples of 90° and 30° because the spontaneous strain deforms the twin orientations. All orientations were reproduced from the Sapriel conditions that twin walls are unstrained in [32].
3. Twin Walls as Storages for Cations and Their Pinning Behaviour in Anorthoclase
Anorthoclase is a prototypic mineral for local exchanges of cations in twin walls. Inscribing and erasing twin domains (so-called ‘twin memory’ and ‘twin amnesia’) was experimentally observed in anorthoclase with composition Ab70 Or25 An5 from volcanic tuffs in Camperdown, Victoria (Sample 195127 in the Harker Collection, Cambridge University) [33]. After collecting the room temperature XRD rocking curve of anorthoclase, a sample was heated rapidly in vacuum to some high temperature above the displacive transition temperature for the sample (733 K); this temperature was then maintained for 4 h. The sample was then cooled back to room temperature (with a cooling rate of ~10 K·min−1), where the rocking curve was again recorded. The cycle of collecting a room temperature rocking curve and heating to progressively higher and higher temperatures was repeated until an annealing temperature of ~1000 K was reached.
Rocking curves clearly reveal the formation of twins. They showed that twins were generated by quenching the sample through the phase transition temperature. This leads to the ‘memory effect’: the twin structure remains stable and it will always reappear at exactly the same locations in the sample when reheated and re-cooled through the transitions. This effect continues until the walls are erased or overwritten by further heating, which qualifies as ‘twin amnesia’. Annealing at 860 K does not induce much twin amnesia, while annealing at 880 K has a much greater effect. The phase diagram for anorthoclase reveals the underlying mechanism. The temperature at which twin memory begins to be lost is near the solvus temperature for anorthoclase with the composition of the Camperdown sample, where segregation between Na and K commences on cooling. Thus, the diffusion K into the twin boundaries was identified as mechanism for the twin memory effect, while the replacement by Na induces amnesia (Figure 3 and Figure 4).
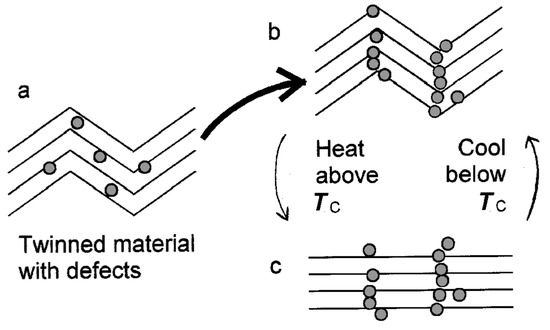
Figure 3. Schematic illustration of atomic-scale mechanism of twin memory in anorthoclase (after [34]).

Figure 4. Typical TEM micrographs of anorthoclase. This image at the left is of a (010) slice of Camperdown anorthoclase, and shows the pericline twins approximately parallel to (001). The image at the right shows a wider view of twinning in an albite rich plagioclase in granite. Twins are seen as narrow lines with two dominant orientations, representing the albite and pericline twin laws. The diameter of the field of view is 3 mm (courtesy Prof. M.A. Carpenter).
The local crystal structure inside the twin boundary differs from that in the bulk [34][35][36][37][38], and this has the effect of attracting Na or K to the twin boundary. Simple symmetry and volume arguments favor the larger K ions on the twin boundaries, and Na in the bulk.
While alkali segregation is the mechanism that is responsible for twin memory in anorthoclase, one expects memory loss to occur quite rapidly once the solvus temperature is exceeded, since alkali diffusion through the feldspar structure is rapid [39], and the diffusion lengths that are required for twin memory are quite small. At room temperature, the twin wall thickness in anorthoclase is of the order of 2.5 nm [40]. Thus, there are sufficient potassium cations to completely fill the twin wall in a relatively narrow layer with a maximum diffusion length required to be of the wall thickness.
This example highlights the effect of ‘loading’ and ‘unloading’ twin walls with cations or defects. In the case of anorthoclase, the change of chemical composition inside twin walls was already observed in 2000 by microprobe techniques [36]. Such chemical changes, in turn, pin the position of twin walls, so that the twin walls appear to be static under weak fields while the un-doped sample shows freely moving twin boundaries. This effect was also simulated by computational molecular dynamics methods [41]. The results show that randomly distributed, static defects are enriched in ferroelastic domain walls. Quantitatively, the relative concentration of defects in walls, Nd, follows a power law distribution as a function of the total defect concentration C: Nd ~ Cα with α = 0.4. In these simulations, the enrichment Nd/C ranges from ca. 50 times to ~3 times. The enrichment is due to the nucleation of twins at defect sites; the dynamics of twin nucleation and switching are then strongly dependent on the defect concentration. Under stress, the domain walls do no longer move smoothly, but form avalanches. This phenomenon is rather common when walls de-pin and nucleate new walls, see the reviews in [16][42][43][44][45][46]. The energy distributions of these avalanches follow power laws with energy exponents ε between 1.33 and 2.7. These exponents then allow for a detailed characterization of the pinning behavior and assessment how much the twin structures adapt to the defect distribution (Figure 5 and Figure 6).
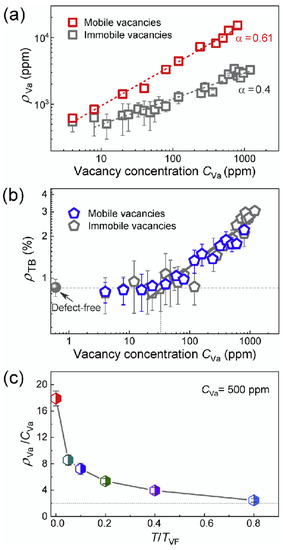
Figure 5. (a) The relative concentration of vacancies at boundaries rVa as a function of the vacancy concentration CVa at T = 5 × 10−4 TVF. TVF is the Vogel-Fulcher temperature of the twin mobility. For mobile vacancies, after long time diffusion, it follows a power law rVa ~ CVa α with α = 0.61 (red data). The grey square shows the immobile vacancy. (b) The variation of twin boundary density rTB with CVa at T = 5 × 10−4 TVF follows a power law relationship. As rTB ~ CVa α with α = 1/3. (c) The enrichment ratio of rVa/CVa decreases with increasing temperature and drops to ca. 2.45 at T = 0.8TVF. Reproduced with permission from [47] published by Elsevier Ltd., 2019.
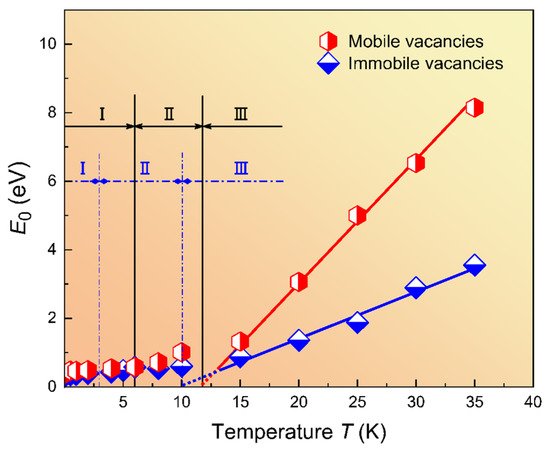
Figure 6. Phase diagram for the energy E0 of mobile and immobile vacancies as a function of temperature. E0 is defined as E0 ~ kB(T − TVF), which corresponds to an activation energy at the temperature T. The Vogel–Fulcher temperature is TVF, which is near 12K in this model. Reproduced with permission from [47] published by Elsevier Ltd., 2019.
This mechanism changes when defects have mobilities that are comparable with those of mobile twin walls [47]. Molecular dynamics analysis indicates how vacancies reduce their energy by residing in twin boundaries, kinks inside twin walls, and junctions between twin walls. Vacancies have the largest binding energy inside junctions and they co-migrate with the motion of the junctions between twin walls. For defects trapped inside twin walls, a “ghost line” may be generated, because vacancies do not necessarily diffuse with moving boundaries, similar to the memory effect in anorthoclase. They leave a trace of their previous position when they are left behind. Needle twin walls act as channels for fast diffusion with almost one order of magnitude higher vacancy diffusivity than in the bulk. This modifies the relative concentration of vacancies at twin boundaries as a function of the average vacancy concentration. The concentration of vacancies at twin boundaries is enriched ca. five times at low temperatures, as determined by these simple simulations. With increasing temperature, the enrichment drops as the trapping potential at the twin boundaries decreases via thermal release. The distribution of energy-drops upon twin pattern evolution follows a power law. The energy exponent of the mobile twin walls ε increases from ~1.44 to 2.0 when the vacancy concentration increases. Such enrichments of cations and vacancies in twin walls have been widely reported in the literature (e.g., in perovskites [37], klinker [48], twinned alloys [49], pure metal twin walls [50], cassiterite (SnO2) [51], tellurized molydenite [52], tungsten dichalcogenites [53], and twin wall doping in palmierite [54]. Oxygen vacancy trapping in perovskite was simulated and the results are discussed in [55][56]. The determination of chemical variabilities of twin boundaries have become an active field of research, both experimentally e.g., when trace elements are hidden in twin walls, and by computer simulation.
The chemical changes in twin walls requires that the twin walls have a finite volume. It can be estimated that the typical proportion of atoms in twin walls in a heavily twinned mineral is ca 1–10 ppm. The thickness of the twin walls has been measured for several minerals and it extends over some nanometers (2 nm in palmierite [57], 1.3 nm in anorthoclase [40], 1.6 nm in tungstate [58], 1.6 nm in LaAlO3, [59], and 2 nm in perovskite [60]). In addition, the possibility of thickness measurements by surface methods was raised [61][62][63]. It was argued that twin wall thicknesses will vary significantly with their local chemical composition [64][65]. Nevertheless, the length scale over which the twin walls expand or retract, their thickness remains below 10 nm. Hence, experimental work to quantify this variation is very hard to perform, because other effects, like kink-formation and wiggles in twin walls, will be superimposed onto the compositional effect and may obscure them.
4. Structural Changes and Electric Polarization inside Twin Boundaries in the Mineral Perovskite
Even when twin walls are chemically inert and do not change their composition relative to the twin domains, they will still modify their crystal structure. The simple reason is that the unit cells in twin walls are systematically deformed by the strain that is exerted by the twin domains. A simple sketch presented in Figure 7 shows a simplified lattice configuration with two twins. The repetition lengths between the lattice points have the same length as in the twin domain and in the wall (tainted red in Figure 7). Only the second nearest neighbor lengths across the twin wall are different in the wall from the bulk. This leads to subtle structural differences in the domain and walls. A large cation is then imagined to be inserted in these local cells. While their optimal position in the rectangles is near its midpoint, this is not true for the wall. Here, the atoms will shift towards the upper end of the kite-shapes cells. This simple thought experiment illustrates why large atoms in the twin walls are always shifted with respect to the twin domains, and that these shifts commonly are directed towards the apex of the wall cells.
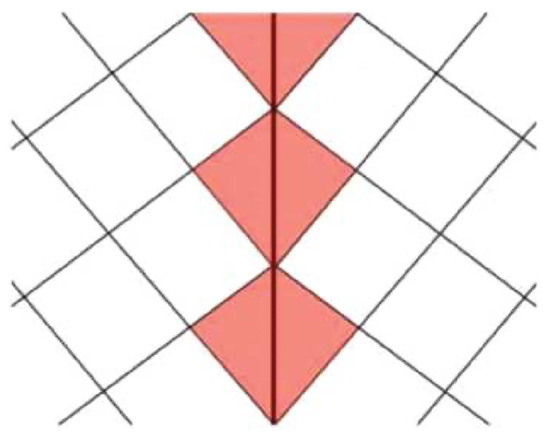
Figure 7. A simple model of a twin wall where the exchange between short and long repetition lengths between second nearest neighbor lattice points leads to a lattice distortion inside the red wall area.
This twin wall effect has been predicted in much more detail using Landau theory [66][67][68]. The structural deviations in the twin walls are substantial and they play a major role in device fabrication [69][70][71] and so-called adaptive materials where the phase equilibria are achieved by suitable twinning processes [72]. A typical example is the twin structure in the mineral perovskite (CaTiO3), where the intrinsic wall activation energy was first calculated by Lee et al. [73]. The breakthrough for the detailed structure determination was achieved by Van Aert et al. [60], who demonstrated, by transmission electron microscopy, that the Ti positions in the twin walls were indeed shifted by 6 pm along the wall direction (Figure 8 and Figure 9). Such large shifts were previously unexpected, and they rank amongst the biggest polar shifts in any mineral. It is comparable with the ferroelectric shift of Ti in the ferroelectric material BaTiO3.
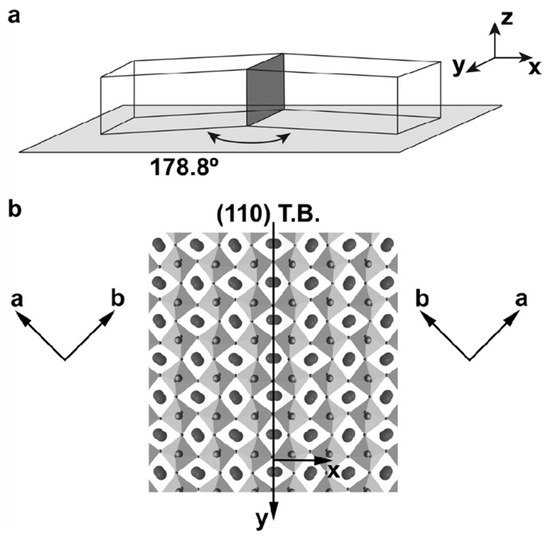
Figure 8. Perovskite CaTiO3 (a) Single twin wall, indicated as standing dark grey plane, with the chosen (x, y, z) reference system for the definitions of the measured displacements. The angle of 178.8° is the result of the twinning operation from the high temperature cubic to the low temperature orthorhombic phase. (b) Atomic configuration on both sides of the (110) twin plane with Ca atoms marked by large, filled circles, Ti atoms by medium-sized shaded circles, and O atoms by small circles. Reproduced with permission from [60], published by John Wiley & Sons, Inc., 2011.
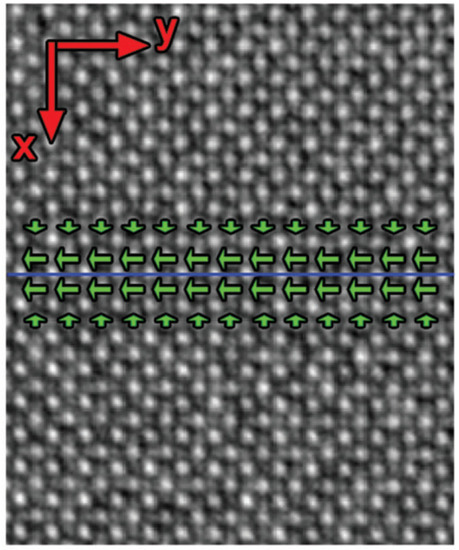
Figure 9. Mean displacements of the Ti atomic columns from the centre of the four neighbouring Ca atomic columns inside the twin wall are indicated by green arrows in perovskite CaTiO3. The centre row of atoms shifts to the left and generates polarity of the domain wall. The polarization perpendicular to the wall is self-compensating. The blue line indicates the middle of the twin boundary. Reproduced with permission from [60], published by John Wiley & Sons, Inc., 2011.
The dramatic structural deformation inside twin walls has been observed in many materials, although it was first discovered in the mineral perovskite. Technically, the measurement of symmetry breaking in twin walls is very involved using transmission electron microscopy. It is greatly eased by using the second harmonic generation, SHG, technique, i.e., the observation of the doubling of the laser frequency in piezoelectric twin walls, as a measure for the local structural distortion. This technique is ideal if the twin domains are centrosymmetric, while the symmetry breaking renders the twin walls piezoelectric. SHG does not see the twin domains in this case, but it gives strong signals of the twin walls [74]. The symmetry relations of the SHG allow for the determination of local point symmetry of the twin wall. Another useful method is phonon spectroscopy [75][76]. Polar twin walls were also confirmed in other minerals, such as palmierite [31][54] and clinobisvanite BiVO4 [77][78]. Very high densities of twin walls, such as in tweed structures, lead to an overall SHG background that proves that the mineral contains an extremely high density of walls that is hard to see using other techniques [79]. The tweed structure, as an extension of the twin structure, was already predicted in the 1990s [80][81][82][83][84][85] and recently observed in LaAlO3. A short review on tweed in minerals can be found in [86]. A typical selection of tweed in minerals is given in [87][88][89][90][91][92]. However, none of these minerals have yet been analyzed in sufficient detail to quantify the local symmetry breaking effects in the twin walls or in the tweed structure.
5. Topological Changes of Twin Walls: Kinks and Surface Intersections
Twin walls are planar in local areas, but not globally. They are prone to topological defects, like kinks, arching, and systematic changes, when they touch surfaces. In addition, they deform dynamically under external stress. This effect is at the core of Resonant Ultrasonic Spectroscopy, RUS. Its application to twins in minerals is far too extensive to be reviewed; here, the reader is referred to the excellent review by Carpenter and Zhang [93], which covers several minerals. Specific examples were discussed [94][95][96][97][98][99]. The underlying mechanisms of these dynamic phenomena of twins were computer simulated [100][101][102] and they show a multitude of mechanisms like the progression and retraction of needles, wall arching and shifts of wall defects [100][101][102][103]. They analyzed the movement of needles domains and wall bending of twin domains, which is retarded by interactions with the crystals structure. These interactions lead to pinning and, hence, to the damping of the wall movement. RUS experiments prove that twin walls are locally mobile, and that damping can be measured quantitatively. Hence, the macroscopic elastic response of a twinned ferroelastic mineral has very little to do with its intrinsic elastic properties, but is greatly reduced by the spatial relaxations and energy absorption of twin walls. Only when the uniaxial stress is large enough to eliminate all twins, will one be able to measure the intrinsic, un-twinned elastic properties. As the scientific question has now turned towards the understanding of twins and their boundaries, elastic measurements need to avoid these excessive stresses. Typical external strains in elastic measurements are in the order of 10−7 to 10−4, i.e., being much lower than typical detwinning strains [104]. The induced wall movements are equally small with resonance amplitudes in the order of several attometers. Only the walls between twin domains contribute to damping, but not the twin domains themselves, which gives excellent access to wall data that are not polluted by bulk effects.
Common perturbations of twin walls are kinks or latches. Figure 10 shows a typical example.
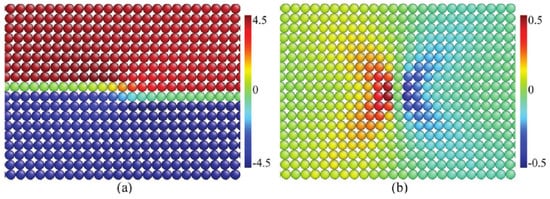
Figure 10. A static kink in a twin wall is shown by (a) the vertical shear angle and (b) the horizontal shear angle. The strain field in (b) is similar to those of shear dislocations. Reproduced with permission from [105], published by John Wiley & Sons, Inc., 2017.
These kinks generate large strain fields perpendicular and parallel to the twin walls. The kinks move along the twin walls when external stresses are applied. The direction of travel is determined by the energy gain by increasing the energetically favorable twin domain and reducing the unfavorable twin domain. The overall location of the twin wall does not change; only the kink inside the twin wall moves until it hits the sample surface. The self-energy of a moving wall diverges in Landau–Ginzburg theory as E ∼ (1 − v2/c2)−0.5, where c is the relevant sound velocity and v is the wall velocity. This divergence stems from the one-dimensional (1D) character of the wall movement where the propagation direction coincides with the strain gradient as discussed in detail in [25]. Kinks do not suffer from this singularity, because the propagation and strain gradient are rotated by 45° with respect to each other, so that any analytical description is intrinsically 2D avoiding the mass renormalization. Nevertheless, moving kinks also dissipate energy, and this dissipation is the “stumbling block” for high-speed applications. Kinks within the most commonly discussed Φ4 model (the self-energy of the kink is a 4th order polynomial) contain “wobbles” as internal degrees of freedom [106]. Certain speeds in excess of the sound barrier are theoretically stable and they generate emanating elastic waves during the propagation of the kink [107]. Molecular dynamics (MD) simulations of “realistic” kinks show that the real situation is rather more intriguing: the kink is first accelerated from a static position to a speed near the transverse sound velocity. Further acceleration leads to a maximum velocity, which is greater than the longitudinal sound velocity. Thus, kinks in a planar wall move at ultrasonic speeds if the driving force is sufficiently strong. The kink profiles change during this movement. Phonons are emitted from the moving kink at all velocities while the static kink only induces a strain field that is similar to that of an edge dislocation. When kinks in twin walls propagate with velocities faster than the various speeds of sound in a mineral, they emit secondary waves (~ ultrasonic ‘bangs’) similar to high-speed projectiles. This effect is speculated to be useful for fast computer memories where the kink position serves as a memory element. Highly twinned leucite is such an example where kinks in twin walls are expected. The first experiments were conducted [108] and they showed that the topological conditions for ultrasonic kinks are favorable. However, the kinks did not contain polarity, or only very weak polarity, so that any electric or magnetic observation of the kink movement would be very difficult.
Magnetic signals of moving kinks in twin walls were computer simulated and they are now predicted for perovskite structures [109]. These results confirm the idea that twins and twin walls commonly produce vortex structures [110][111], as shown in Figure 11.
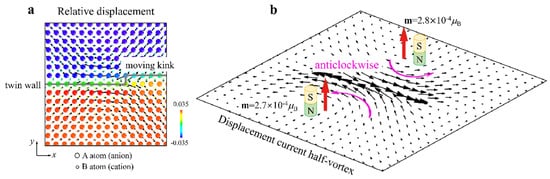
Figure 11. (a) Displacement currents and the corresponding magnetic fields produced by moving a kink inside a twin wall. Relative displacements of cations and anions near the moving kink during a time interval of 0.5 ps. The colours are coded by the atomic-level shear strain. Ionic displacements are amplified by a factor of 50 for clarity. (b) Two half-vortices of the displacement currents rotate in the same direction in both domains. The current density was calculated based on the relative displacements of anions and cations. The local displacement current is ~10−19 A. The magnetic field is ~2.7 × 10−4 μB for each half-vortex (after [109]).
Twin domains are seen at the surface of the mineral, the walls between twin domains appear as lines, which are often referred to as ‘striation’. This leads to the question how the surface properties of a mineral are influenced by the emerging properties of the twin walls. While this problem is greatly discussed in the case of magnetic and ferroelectric materials, much less is known for ferroelastic twin boundaries. The first result is that the surface is bent near the striation line [112][113]. Figure 12 depicts a cut through of the sample perpendicular to the surface. It shows that the surface plane is compressed near the twin boundary, and that long ranging relaxations extend over the surface. These relaxations make the twin boundary appear in optical studies blurred and much wider than their intrinsic geometrical core of some nanometers. The surface forms valleys and ridges where the two twin variants meet at the twin boundary.

Figure 12. Distribution of the order parameter shear deformation (~order parameter Q) at the surface of the lattice (first 50 layers). Lines represent constant Q, with Q0 = 1 in the bulk. There are three lines in the middle of the twin domain wall that are not labelled, they represent the Q values of 0.40, 0.00, and −0.40 respectively. Notice the steepness of the gradient of Q through the twin domain wall. The two structures represent sheared twin atomic configurations in the bulk (far from the twin domain wall and surfaces). Reproduced with permission from [112], published by IOP Publishing Ltd., 1998.
When the mineral is not mono-atomic, the cations and anions will form dipoles, as discussed above. When these dipoles approach the surface, they are modified by surface relaxations [114], as shown in Figure 13.
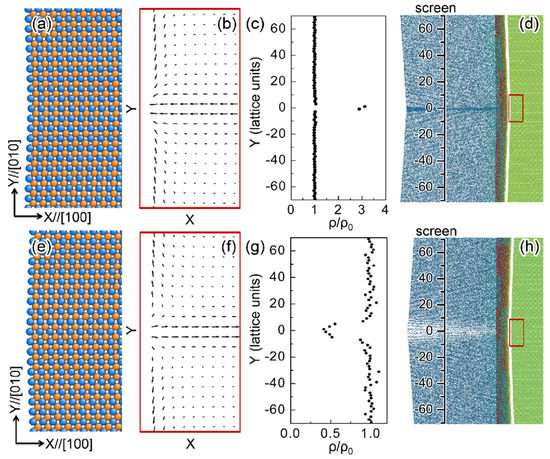
Figure 13. Polarity at anion-terminated surfaces. (a,b) The atomic configurations and polarizations near twin boundary I (a valley). The dipole displacement is amplified by a factor of 25 for clarity. Cations are colored in orange and anions are colored in blue. (c,d) A snapshot illustrates incident electrons being reflected by the surface. Red electrons are approaching the surface and blue electrons are departing from the surface (the mixture gives rise to the gray color of the electrons). The red rectangle in the green sample indicates the region shown in (a) and (b). The reduced density (ρ/ρ0) of electrons projected on the virtual screen is shown in (c), ρ0 is the electron density in the initial configuration. (e–h) are the corresponding results for twin boundary II (a ridge). Reproduced with permission from [114]), published by American Physical Society, 2019.
The electron scattering MEM image shown in Figure 14 shows the intricate twin pattern in a perovskite mineral (a) and the equivalent AFM pattern (b). The twin domains show the same surface charges and, hence, no variation in the surface polarization. In contrast, the twin walls show the typical positive or negative surface polarization, which confirms the fact that twin walls in perovskite are polar and piezoelectric.

Figure 14. (a) Experimental images of electron back scattered MEM image of the CaTiO3 (111) surface showing bright and dark domain walls. Far from the domain wall there is no surface potential contrast between domains. The domain walls are either dark or bright lines, reflecting positive or negative surface topological charge (upward- or downwards-pointing polarity). The orange square is the zone analysed by AFM in (b). Reproduced with permission from [114]), published by American Physical Society, 2019.
6. Outlook
Twin structures were well studied in several minerals. Their remarkable feature is that the joint between twins is not simply a ‘glue’ that holds the twins together, but a highly complex structural unit that differs greatly from the atomic structure of the twin domains. The simple interpolation between atomic positions of adjacent twin domains does not yield the structure of the twin wall. Many exciting properties exist only in the twin wall, but not in the twin domains. Some were discussed in this short review, such as chemical storage, polarity, piezoelectricity, topological defects, like kinks, and surface deformations. This observation leads to the question of what happens to twins in minerals that are not ferroelastic [115]. Growth twins are an excellent candidate for further research. We have no information regarding the atomic structure of such twin walls, but we may speculate that the same principles, which were discussed in this paper, also apply. An atypical example is the twinning in cordierte that contains ferroelastic and topological aspects [116]. This means that these twinned minerals may contain a multitude of ‘emerging’ properties that we simply do not know. They may contain pockets of material with homeopathic doses of dopants and novel structural elements which are stable only under the geometrical confinement of the twin wall. This has significantly wider consequences: many properties of solids have first been found in minerals before laboratory-based work reproduced the same materials for technological applications. This ‘learning from nature’ served us well over the last decades. It may well be, I beg to predict, that some of the most exciting properties that are related to twinning are still to be discovered.
References
- Kunz, G.F. The Life and Work of Haüy. Am. Miner. 1918, 3, 59–89.
- Gruner, J.W. Structural reasons for oriented intergrowths in some minerals. Am. Miner. 1929, 14, 227–237.
- Aminoff, G.; Broomé, B. Strukturtheoretische Studien über Zwillinge. I. Z. Für Krist. Cryst. Mater. 1931, 80, 355–376.
- Taylor, W.H.; Darbyshire, J.A.; Strunz, H. An X-ray investigation of the felspars. Z. Für Krist. Cryst. Mater. 1934, 87, 464–498.
- Zachariasen, W.H. The Crystal Structure of Sodium Formate, NaHCO21. J. Am. Chem. Soc. 1940, 62, 1011–1013.
- Friedel, G. Leçons de Cristallographie; Berger-Levrault: Paris, France, 1926.
- Goldsmith, J.R.; Laves, F. Uber die Mischkristallreihe Mikrokline-Albite. Angew. Chem. 1956, 68, 755–756.
- Bragg, W.L. Geological Magazine, London: Humphrey Milford; Oxford University Press: Oxford, UK, 1937.
- Strunz, H. Systematik und Struktur der Silikate. Z. Für Krist. Cryst. Mater. 1938, 98, 60–83.
- Klockmann’s Lehrbuch der Mineralogie. Paul Ramdohr. J. Geol. 1955, 63, 99.
- Aird, A.; Salje, E.K.H. Sheet superconductivity in twin walls: Experimental evidence of. J. Phys. Condens. Matter 1998, 10, L377.
- Aird, A.; Domeneghetti, M.C.; Mazzi, F.; Tazzoli, V.; Salje, E.K.H. Sheet superconductivity in WO3: Crystal structure of the tetragonal matrix. J. Phys. Condens. Matter 1998, 10, L569.
- Kim, Y.; Alexe, M.; Salje, E.K.H. Nanoscale properties of thin twin walls and surface layers in piezoelectric WO3−x. Appl. Phys. Lett. 2010, 96, 032904.
- Salje, E.K.H. Multiferroic Domain Boundaries as Active Memory Devices: Trajectories Towards Domain Boundary Engineering. ChemPhysChem 2010, 11, 940–950.
- Salje, E.; Zhang, H. Domain boundary engineering. Phase Transit. 2009, 82, 452–469.
- Nataf, G.F.; Salje, E.K.H. Avalanches in ferroelectric, ferroelastic and coelastic materials: Phase transition, domain switching and propagation. Ferroelectrics 2020, 569, 82–107.
- Nataf, G.F.; Guennou, M.; Gregg, J.M.; Meier, D.; Hlinka, J.; Salje, E.K.H.; Kreisel, J. Domain-wall engineering and topological defects in ferroelectric and ferroelastic materials. Nat. Rev. Phys. 2020, 2, 634–648.
- Carpenter, M.A.; Salje, E.K.H.; Graeme-Barber, A.; Wruck, B.; Dove, M.T.; Knight, K.S. Calibration of excess thermodynamic properties and elastic constant variations associated with the alpha beta phase transition in quartz. Am. Miner. 1998, 83, 2–22.
- Salje, E.K.H.; Ridgwell, A.; Guttler, B.; Wruck, B.; Dove, M.T.; Dolino, G. On the displacive character of the phase transition in quartz: A hard-mode spectroscopy study. J. Phys. Condens. Matter 1992, 4, 571.
- Calleja, M.; Dove, M.T.; Salje, E.K.H. Anisotropic ionic transport in quartz: The effect of twin boundaries. J. Phys. Condens. Matter 2001, 13, 9445–9454.
- Salje, E.; Kuscholke, B.; Wruck, B.; Kroll, H. Thermodynamics of sodium feldspar II: Experimental results and numerical calculations. Phys. Chem. Miner. 1985, 12, 99–107.
- Salje, E. Thermodynamics of sodium feldspar I: Order parameter treatment and strain induced coupling effects. Phys. Chem. Min. 1985, 12, 93–98.
- Tsatskis, I.; Salje, E.K.H. Time evolution of pericline twin domains in alkali feldspars; a computer-simulation study. Am. Miner. 1996, 81, 800–810.
- Salje, E.; Kuscholke, B.; Wruck, B. Domain wall formation in minerals: I. theory of twin boundary shapes in Na-feldspar. Phys. Chem. Miner. 1985, 12, 132–140.
- Salje, E.K. Phase Transitions in Ferroelastic and Co-Elastic Crystals; Cambridge University Press: Cambridge, UK, 1993; ISBN 0521429366.
- Salje, E.K.H. Application of Landau theory for the analysis of phase transitions in minerals. Phys. Rep. 1992, 215, 49–99.
- Carpenter, M.A.; Salje, E.K.H. Elastic anomalies in minerals due to structural phase transitions. Eur. J. Miner. 1998, 10, 693–812.
- Carpenter, M.A.; Salje, E.K.H.; Graeme-Barber, A. Spontaneous strain as a determinant of thermodynamic properties for phase transitions in minerals. Eur. J. Mineral. 1998, 10, 621–691.
- Carpenter, M.A.; Salje, E. Time-dependent Landau theory for order/disorder processes in minerals. Mineral. Mag. 1989, 53, 483–504.
- Sapriel, J. Domain-wall orientations in ferroelastics. Phys. Rev. B Condens. Matter 1975, 12, 5128–5140.
- Yokota, H.; Matsumoto, S.; Salje, E.K.H.; Uesu, Y. Polar nature of domain boundaries in purely ferroelastic Pb3(PO4)2 investigated by second harmonic generation microscopy. Phys. Rev. B 2019, 100, 024101.
- Bismayer, U.; Salje, E. Ferroelastic phases in Pb3(PO4)2–Pb3(AsO4)2; X-ray and optical experiments. Acta Crystallogr. Sect. A 1981, 37, 145–153.
- Hayward, S.A.; Salje, E.K.H. Twin memory and twin amnesia in anorthoclase. Miner. Mag. 2000, 64, 195–200.
- Hayward, S.A.; Salje, E.K.H.; Chrosch, J. Local fluctuations in feldspar frameworks. Mineral. Mag. 1998, 62, 639–645.
- Salje, E.K.H.; Bismayer, U.; Hayward, S.A.; Novak, J. Twin walls and hierarchical mesoscopic structures. Miner. Mag. 2000, 64, 201–211.
- Cámara, F.; Doukhan, J.C.; Salje, E.K.H. Twin walls in anorthoclase are enriched in alkali and depleted in Ca and Al. Phase Transit. 2000, 71, 227–242.
- Aird, A.; Salje, E.K.H. Enhanced reactivity of domain walls in with sodium. Eur. Phys. J. B Condens. Matter Complex. Syst. 2000, 15, 205–210.
- Salje, E.K.H. Fast Ionic Transport Along Twin Walls in Ferroelastic Minerals. In Properties of Complex Inorganic Solids 2; Springer: Berlin/Heidelberg, Germany, 2000; pp. 3–15.
- Yund, R.A.; Quigley, J.; Tullis, J. The effect of dislocations on bulk diffusion in feldspars during metamorphism. J. Metamorph. Geol. 1989, 7, 337–341.
- Hayward, S.A.; Chrosch, J.; Salje, E.K.H.; Carpenter, M.A. Thickness of pericline twin walls in anorthoclase: An X-ray diffraction study. Eur. J. Mineral. 1997, 8, 1301–1310.
- He, X.; Salje, E.K.H.; Ding, X.; Sun, J. Immobile defects in ferroelastic walls: Wall nucleation at defect sites. Appl. Phys. Lett. 2018, 112, 092904.
- Casals, B.; Nataf, G.F.; Salje, E.K.H. Avalanche criticality during ferroelectric/ferroelastic switching. Nat. Commun. 2021, 12, 345.
- Casals, B.; Nataf, G.F.; Pesquera, D.; Salje, E.K.H. Avalanches from charged domain wall motion in BaTiO3 during ferroelectric switching. Appl. Mater. 2020, 8, 011105.
- Salje, E.K.H.; Ding, X.; Zhao, Z.; Lookman, T.; Saxena, A. Thermally activated avalanches: Jamming and the progression of needle domains. Phys. Rev. B Condens. Matter 2011, 83, 104109.
- Harrison, R.J.; Salje, E.K.H. Ferroic switching, avalanches, and the Larkin length: Needle domains in LaAlO3. Appl. Phys. Lett. 2011, 99, 151915.
- Salje, E.K.H.; Dahmen, K.A. Crackling Noise in Disordered Materials. Annu. Rev. Condens. Matter Phys. 2014, 5, 233–254.
- He, X.; Li, S.; Ding, X.; Sun, J.; Selbach, S.M.; Salje, E.K.H. The interaction between vacancies and twin walls, junctions, and kinks, and their mechanical properties in ferroelastic materials. Acta Mater. 2019, 178, 26–35.
- Saidani, S.; Smith, A.; El Hafiane, Y.; Ben Tahar, L. Role of dopants (B, P and S) on the stabilization of β-Ca2SiO4. J. Eur. Ceram. Soc. 2021, 41, 880–891.
- Qin, H.; Zhu, J.; Li, N.; Wu, H.; Guo, F.; Sun, S.; Qin, D.; Pennycook, S.J.; Zhang, Q.; Cai, W.; et al. Enhanced mechanical and thermoelectric properties enabled by hierarchical structure in medium-temperature Sb2Te3 based alloys. Nano Energy 2020, 78, 105228.
- Boryakov, A.V.; Gladilin, A.A.; Il’ichev, N.N.; Kalinushkin, V.P.; Mironov, S.A.; Rezvanov, R.R.; Uvarov, O.V.; Chegnov, V.P.; Chegnova, O.I.; Chukichev, M.V.; et al. The Influence of Annealing in Zinc Vapor on the Visible and Mid-IR Luminescence of ZnSe:Fe2+. Opt. Spectrosc. 2020, 128, 1844–1850.
- Padrón-Navarta, J.A.; Barou, F.; Daneu, N. Twinning in SnO2-based ceramics doped with CoO and Nb2O5: Morphology of multiple twins revealed by electron backscatter diffraction. Acta Cryst. B Struct Sci Cryst Eng. Mater. 2020, 76, 875–883.
- Ji, X.; Krishnamurthy, M.N.; Lv, D.; Li, J.; Jin, C. Post-synthesis Tellurium Doping Induced Mirror Twin Boundaries in Monolayer Molybdenum Disulfide. Appl. Sci. 2020, 10, 4758.
- Wang, B.; Xia, Y.; Zhang, J.; Komsa, H.-P.; Xie, M.; Peng, Y.; Jin, C. Niobium doping induced mirror twin boundaries in MBE grown WSe2 monolayers. Nano Res. 2020, 13, 1889–1896.
- Yokota, H.; Matsumoto, S.; Hasegawa, N.; Salje, E.K.H.; Uesu, Y. Enhancement of polar nature of domain boundaries in ferroelastic Pb3(PO4)2 by doping divalent-metal ions. J. Phys. Condens. Matter 2020, 32, 345401.
- Calleja, M.; Dove, M.T.; Salje, E.K.H. Trapping of oxygen vacancies on twin walls of CaTiO3: A computer simulation study. J. Phys. Condens. Matter 2003, 15, 2301–2307.
- Goncalves-Ferreira, L.; Redfern, S.A.T.; Artacho, E.; Salje, E.; Lee, W.T. Trapping of oxygen vacancies in the twin walls of perovskite. Phys. Rev. B 2010, 81, 024109.
- Wruck, B.; Salje, E.K.H.; Zhang, M.; Abraham, T.; Bismayer, U. On the thickness of ferroelastic twin walls in lead phosphate Pb3(PO4)2 an X-ray diffraction study. Phase Transit. 1994, 48, 135–148.
- Locherer, K.R.; Chrosch, J.; Salje, E.K.H. Diffuse X-ray scattering in WO3. Phase Transit. 1998, 67, 51–63.
- Chrosch, J.; Salje, E.K.H. Temperature dependence of the domain wall width in LaAlO3. J. Appl. Phys. 1999, 85, 722–727.
- Van Aert, S.; Turner, S.; Delville, R.; Schryvers, D.; Van Tendeloo, G.; Salje, E.K.H. Direct observation of ferrielectricity at ferroelastic domain boundaries in CaTiO3 by electron microscopy. Adv. Mater. 2012, 24, 523–527.
- Salje, E.K.H.; Lee, W.T. Pinning down the thickness of twin walls. Nat. Mater. 2004, 3, 425–426.
- Lee, W.T.; Salje, E.K.H.; Bismayer, U. Surface relaxations at mineral surfaces. Z. Für Krist. Cryst. Mater. 2005, 220, 683–690.
- Lee, W.T.; Salje, E.K.H. Chemical turnstile. Appl. Phys. Lett. 2005, 87, 143110.
- Shilo, D.; Mendelovich, A.; Novák, V. Investigation of twin boundary thickness and energy in CuAlNi shape memory alloy. Appl. Phys. Lett. 2007, 90, 193113.
- Shilo, D.; Ravichandran, G.; Bhattacharya, K. Investigation of twin-wall structure at the nanometre scale using atomic force microscopy. Nat. Mater. 2004, 3, 453–457.
- Houchmandzadeh, B.; Lajzerowicz, J.; Salje, E. Order parameter coupling and chirality of domain walls. J. Phys. Condens. Matter 1991, 3, 5163–5169.
- Houchmanzadeh, B.; Lajzerowicz, J.; Salje, E. Interfaces and ripple states in ferroelastic crystals—A simple model. Phase Transit. 1992, 38, 77–87.
- Houchmandzadeh, B.; Lajzerowicz, J.; Salje, E. Relaxations near surfaces and interfaces for first-, second- and third-neighbour interactions: Theory and applications to polytypism. J. Phys. Condens. Matter 1992, 4, 9779–9794.
- Salje, E.K.H. Ferroelastic domain walls as templates for multiferroic devices. J. Appl. Phys. 2020, 128, 164104.
- Salje, E.K.H.; Aktas, O.; Carpenter, M.A.; Laguta, V.V.; Scott, J.F. Domains within domains and walls within walls: Evidence for polar domains in cryogenic SrTiO3. Phys. Rev. Lett. 2013, 111, 247603.
- Aktas, O.; Salje, E.K.H.; Crossley, S.; Lampronti, G.I.; Whatmore, R.W.; Mathur, N.D.; Carpenter, M.A. Ferroelectric precursor behavior in PbSc0.5Ta0.5O3detected by field-induced resonant piezoelectric spectroscopy. Phys. Rev. B 2013, 88, 174112.
- Viehland, D.D.; Salje, E.K.H. Domain boundary-dominated systems: Adaptive structures and functional twin boundaries. Adv. Phys. 2014, 63, 267–326.
- Lee, W.T.; Salje, E.K.H.; Goncalves-Ferreira, L.; Daraktchiev, M.; Bismayer, U. Intrinsic activation energy for twin-wall motion in the ferroelastic perovskite CaTiO3. Phys. Rev. B Condens. Matter 2006, 73, 214110.
- Yokota, H.; Usami, H.; Haumont, R.; Hicher, P.; Kaneshiro, J.; Salje, E.K.H.; Uesu, Y. Direct evidence of polar nature of ferroelastic twin boundaries inCaTiO3 obtained by second harmonic generation microscope. Phys. Rev. B 2014, 89, 144109.
- Salje, E.K.H. Hard mode Spectroscopy: Experimental studies of structural phase transitions. Phase Transit. 1992, 37, 83–110.
- Nataf, G.F.; Guennou, M. Optical studies of ferroelectric and ferroelastic domain walls. J. Phys. Condens. Matter 2020, 32, 183001.
- Yokota, H.; Hasegawa, N.; Glazer, M.; Salje, E.K.H.; Uesu, Y. Direct evidence of polar ferroelastic domain boundaries in semiconductor BiVO4. Appl. Phys. Lett. 2020, 116, 232901.
- Bridge, P.J.; Pryce, M.W. Clinobisvanite, monoclinic BiVO4, a new mineral from Yinnietharra, Western Australia. Mineral. Mag. 1974, 39, 847–849.
- Yokota, H.; Haines, C.R.S.; Matsumoto, S.; Hasegawa, N.; Carpenter, M.A.; Heo, Y.; Marin, A.; Salje, E.K.H.; Uesu, Y. Domain wall generated polarity in ferroelastics: Results from resonance piezoelectric spectroscopy, piezoelectric force microscopy, and optical second harmonic generation measurements in LaAlO3 with twin and tweed microstructures. Phys. Rev. B 2020, 102, 104117.
- Salje, E.; Parlinski, K. Microstructures in high Tc superconductors. Supercond. Sci. Technol. 1991, 4, 93.
- Parlinski, K.; Heine, V.; Salje, E.K.H. Origin of tweed texture in the simulation of a cuprate superconductor. J. Phys. Condens. Matter 1993, 5, 497–518.
- Wang, X.; Salje, E.K.H.; Sun, J.; Ding, X. Glassy behavior and dynamic tweed in defect-free multiferroics. Appl. Phys. Lett. 2018, 112, 012901.
- Bratkovsky, A.M.; Marais, S.C.; Heine, V.; Salje, E.K.H. The theory of fluctuations and texture embryos in structural phase transitions mediated by strain. J. Phys. Condens. Matter 1994, 6, 3679.
- Putnis, A.; Salje, E. Tweed microstructures: Experimental observations and some theoretical models. Phase Transit. 1994, 48, 85–105.
- Bratkovsky, A.M.; Salje, E.K.H.; Heine, V. Overview of the origin of tweed texture. Phase Transitions 1994, 52, 77–83.
- Salje, E.K.H. Tweed, twins, and holes. Am. Miner. 2015, 100, 343–351.
- Tribaudino, M.; Benna, P.; Bruno, E. I 1-I 2/c phase transition in alkaline-earth feldspars: Evidence from TEM observations of Sr-rich feldspar along the CaAl2Si2O8-SrAl2Si2O8 join. Am. Miner. 1995, 80, 907–915.
- Janney, D.E.; Wenk, H.-R. Peristerite exsolution in metamorphic plagioclase from the Lepontine Alps: An analytical and transmission electron microscope study. Am. Miner. 1999, 84, 517–527.
- McGuinn, M.D.; Redfern, S.A.T. High-temperature ferroelastic strain below the I2/c-I1 transition in Ca1−xSrxAl2Si2O8 feldspars. Eur. J. Miner. 1997, 9, 1159–1172.
- Viehland, D.; Dai, X.H.; Li, J.F.; Xu, Z. Effects of quenched disorder on La-modified lead zirconate titanate: Long- and short-range ordered structurally incommensurate phases, and glassy polar clusters. J. Appl. Phys. 1998, 84, 458–471.
- Lee, M.R.; Hodson, M.E.; Parsons, I. The role of intragranular microtextures and microstructures in chemical and mechanical weathering: Direct comparisons of experimentally and naturally weathered alkali feldspars. Geochim. Cosmochim. Acta 1998, 62, 2771–2788.
- Lee, M.R.; Brown, D.J.; Smith, C.L.; Hodson, M.E.; MacKenzie, M.; Hellmann, R. Characterization of mineral surfaces using FIB and TEM: A case study of naturally weathered alkali feldspars. Am. Miner. 2007, 92, 1383–1394.
- Carpenter, M.A.; Zhang, Z. Anelasticity maps for acoustic dissipation associated with phase transitions in minerals. Geophys. J. Int. 2011, 186, 279–295.
- Carpenter, M.A. Static and dynamic strain coupling behaviour of ferroic and multiferroic perovskites from resonant ultrasound spectroscopy. J. Phys. Condens. Matter 2015, 27, 263201.
- Perks, N.J.; Zhang, Z.; Harrison, R.J.; Carpenter, M.A. Strain relaxation mechanisms of elastic softening and twin wall freezing associated with structural phase transitions in (Ca,Sr)TiO3 perovskites. J. Phys. Condens. Matter 2014, 26, 505402.
- Oravova, L.; Zhang, Z.; Church, N.; Harrison, R.J.; Howard, C.J.; Carpenter, M.A. Elastic and anelastic relaxations accompanying magnetic ordering and spin-flop transitions in hematite, Fe2O3. J. Phys. Condens. Matter 2013, 25, 116006.
- Zhang, Z.; Koppensteiner, J.; Schranz, W.; Carpenter, M.A. Variations in elastic and anelastic properties of Co3O4 due to magnetic and spin-state transitions. Am. Mineral. 2012, 97, 399–406.
- Zhang, Z.; Schranz, W.; Carpenter, M.A. Acoustic attenuation due to transformation twins in CaCl2: Analogue behaviour for stishovite. Phys. Earth Planet. Inter. 2012, 206–207, 43–50.
- Carpenter, M.A.; Salje, E.K.H.; Howard, C.J. Magnetoelastic coupling and multiferroic ferroelastic/magnetic phase transitions in the perovskite KMnF3. Phys. Rev. B Condens. Matter Mater. Phys. 2012, 85, 224430.
- Salje, E.K.H.; Zhao, Z.; Ding, X.; Sun, J. Mechanical spectroscopy in twinned minerals: Simulation of resonance patterns at high frequencies. Am. Miner. 2013, 98, 1449–1458.
- Zhao, Z.; Ding, X.; Lookman, T.; Sun, J.; Salje, E.K.H. Mechanical loss in multiferroic materials at high frequencies: Friction and the evolution of ferroelastic microstructures. Adv. Mater. 2013, 25, 3244–3248.
- Salje, E.K.H.; Ding, X.; Zhao, Z.; Lookman, T. How to generate high twin densities in nano-ferroics: Thermal quench and low temperature shear. Appl. Phys. Lett. 2012, 100, 222905.
- Kustov, S.; Liubimova, I.; Salje, E.K.H. Domain Dynamics in Quantum-Paraelectric SrTiO3. Phys. Rev. Lett. 2020, 124, 016801.
- Kustov, S.; Liubimova, I.; Salje, E.K.H. LaAlO3: A substrate material with unusual ferroelastic properties. Appl. Phys. Lett. 2018, 112, 042902.
- Salje, E.K.H.; Wang, X.; Ding, X.; Scott, J.F. Ultrafast switching in avalanche-driven ferroelectrics by supersonic kink movements. Adv. Funct. Mater. 2017, 27, 1700367.
- Kälbermann, G. The sine-Gordon wobble. J. Phys. A Math. Gen. 2004, 37, 11603–11612.
- Barashenkov, I.V.; Oxtoby, O.F. Wobbling kinks in Φ4 theory. Phys. Rev. E 2009, 80, 026608.
- Aktas, O.; Carpenter, M.A.; Salje, E.K.H. Elastic softening of leucite and the lack of polar domain boundaries. Am. Miner. 2015, 100, 2159–2162.
- Lu, G.; Li, S.; Ding, X.; Sun, J.; Salje, E.K.H. Current vortices and magnetic fields driven by moving polar twin boundaries in ferroelastic materials. NPJ Comput. Mater. 2020, 6, 1–6.
- Salje, E.K.H.; Li, S.; Stengel, M.; Gumbsch, P.; Ding, X. Flexoelectricity and the polarity of complex ferroelastic twin patterns. Phys. Rev. B Condens. Matter 2016, 94, 024114.
- Zhao, Z.; Ding, X.; Salje, E.K.H. Flicker vortex structures in multiferroic materials. Appl. Phys. Lett. 2014, 105, 112906.
- Novak, J.; Salje, E.K.H. Surface structure of domain walls. J. Phys. Condens. Matter 1998, 10, L359–L366.
- Conti, S.; Weikard, U. Interaction between free boundaries and domain walls in ferroelastics. Eur. Phys. J. B Condens. Matter Complex. Syst. 2004, 41, 413–420.
- Zhao, Z.; Barrett, N.; Wu, Q.; Martinotti, D.; Tortech, L.; Haumont, R.; Pellen, M.; Salje, E.K.H. Interaction of low-energy electrons with surface polarity near ferroelastic domain boundaries. Phys. Rev. Mater. 2019, 3, 043601.
- Salje, E.K.H. Ferroelastic materials. Annu. Rev. Mater. Res. 2012, 42, 265–283.
- Blackburn, J.F.; Salje, E.K.H. Time evolution of twin domains in cordierite: A computer simulation study. Phys. Chem. Miner. 1999, 26, 275–291.




