1. Introduction

The challenges associated with the growing world population and the increased degree of interconnection of electronic devices worldwide bring about an increase in energy consumption, which needs to be tackled off-grid by a new generation of stand-alone electrical energy storage systems (EESSs) compensating for the discontinuity of renewable energy sources ^[1]. In fact, renewable energies are unavailable for long periods (e.g., solar energy is predominantly available in the daytime and wind energy in the early mornings). Hence, converting harvested renewable energy to electrical energy and storing it to be readily available anytime for the needs of electronic devices is the primary solution. To achieve this, efficient EESSs tuned to specific applications are needed. EESSs can be broadly classified into four main classes, such as (1) solid oxide fuel cells; (2) traditional batteries (Li-ion batteries); (3) electrochemical capacitors, and (4) dielectric capacitors ^[2]. These EESS classes' appropriateness for a specific application is generally decided by two important parameters, namely the energy density (ED) and the power density. The ED is the energy stored in a given amount of substance, expressed in volume (volumetric ED: Wh/L or J/cm³) or mass (Specific ED: Wh/kg). Power density is the measure of power output from a particular amount of substance and is often expressed in W/kg. A Ragone plot, named after David. V. Ragone ^[3], is often used to show the energy and power available for a certain load, i.e., energy density vs. power density. Here, it is important to note that the Ragone plot depicts the maximum energy in a finite power region that is based on the type of EESSs. The loss mechanisms, such as leakage currents, internal heating, etc., are not included in a Ragone plot, although they are crucial for end applications.

From the Ragone plot shown in Figure 1, it is clear that EESSs have to be chosen depending on the needs because an EESS that combines high power and ED is currently unavailable. In much simpler terms, this plot shows why traditional batteries can supply energy for a longer time (>100 s) but need more time to replenish compared to a dielectric capacitor (<0.01 s). Despite the low ED of dielectric capacitors (cf. Figure 1), higher operating voltages, lower cost, size flexibility, thermal and cyclic stability, and range of possibilities to tune the leakage currents are some of the major advantages. Realizing high ED in a dielectric capacitor while retaining its high-power density would set up new possibilities towards versatility, cost-effectiveness, miniaturization, etc. ^[4].

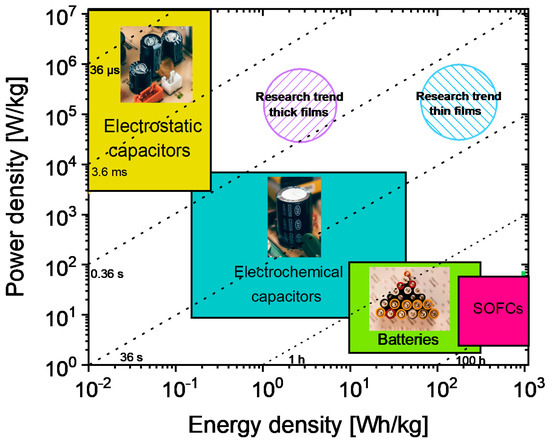
Figure 1. Ragone plot comparing energy density against power density for different electrical energy storage systems (EESSs).

Dielectrics are materials with high electrical resistivity, typically greater than 10⁸ Ω·m and can store electrical energy through lattice polarization resulting from the formation or reorientation of electric dipoles. When a dielectric is placed in an electric field, there is no long-range flow of charge; however, atoms or ions locally react to oppose the electric field by polarizing or setting up a dipole moment that opposes the external applied electric field ^[5]. Hence, dielectric capacitors can quickly deliver charges whereas traditional batteries rely on chemical reactions, making them less time-efficient. Dielectric capacitors can also have a longer lifetime for the very reason contrary to batteries in which the chemical reactions are not always completely reversible.

For a ceramic dielectric, the stored ED, J_s, is given by,

where ε_o is the permittivity of the free space, ε_r is the dielectric permittivity of the ceramic material and E is the applied electric field. J_s can be represented as an integral function of polarization (P) since P = εrE,

The above equations represent the amount of energy that can be stored in a ceramic dielectric when the polarization is increased from 0 to polarization saturation (P_s) under the applied field increasing from 0 to E_max, respectively.

Whereas the recoverable energy density will be,

where P_r is the remnant polarization. Based on these equations, for superior ED properties, a ceramic dielectric should have high ε_r, large P_s, low P_r, and high dielectric breakdown strength (BDS). The BDS is one of the primary deciding factors of ED properties of EESSs ^[6]. Dielectrics with all the stated properties originate from the broad class of ferroelectric materials.

2. Perovskite-Based Relaxor Ferroelectrics

Ferroelectrics (FE) are polar materials with spontaneous polarization that can be reoriented by changing the direction of the external applied electric field. In general, the overall polarization of the ferroelectric crystal is zero because of the equal number of domains oriented in random directions. As E increases, the cations obtain sufficient energy to overcome the local electrical potential barrier and will be able to jump from one random potential well position to another permissible well position most closely aligned with the field, which results in switching of domains. At strong enough E (E_max), switching will result in a domain saturation state (i.e., at the field above which no further domain reorientation in field direction is possible) at which the exhibited polarization is the P_s. Upon reducing and reversing E, the converse process takes place, but traces along a new path consistent with the creation of new domains in the opposite direction. The polarization exhibited at zero field after field reduction is P_r, which is not equal to zero in a FE material. The required E that can switch the ferroelectric material domains back and forth is the coercive field (E_c). Once poled, the material continues to follow the hysteresis loop and will return to zero net polarization at −E_c or if the material is raised above T_c, but not at E = 0 ^[7]. This phenomenon is called polarization-electric field (PE) hysteresis; shown in Figure 2 for a ferroelectric material. Also shown in Figure 2 is the polarization versus electric field (P–E) for relaxors and linear dielectrics.

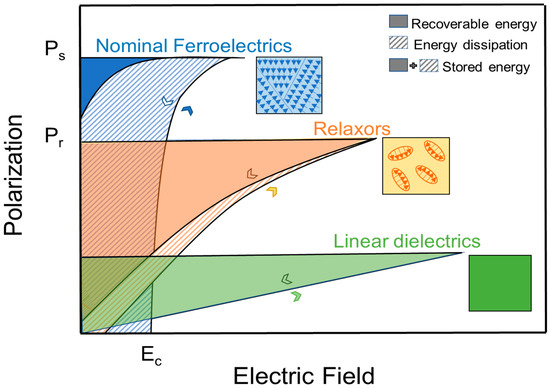
Figure 2. Polarization versus electric field (P−E) for typical ferroelectrics, relaxors, and linear dielectrics.

Because of P−E hysteresis, the recoverable ED, J_r, is usually smaller than J_s in ferroelectric ceramics, as shown in Figure 2. The figure marks the difference in stored and recovered energy in ferroelectric materials by stripes and fillings. The ratio of J_r and J_s is the energy-storage efficiency η.

The difference in J_s and J_r is a direct consequence of non-zero P_r and J_r can be drastically different with different P_r values, also shown in Figure 2 (nominal ferroelectrics vs. relaxors).

Ferroelectricity is reported in four material classes: (1) Oxygen octahedral group (i.e., perovskite) (2) pyrochlore group (3) tungsten-bronze group, and (4) bismuth layer–structure group ^[8]. From a structural point of view, FE materials belong to non-centrosymmetric point groups with orientable spontaneous polarization. From an electrical point of view, an FE material, in addition to the defined P–E loops, will exhibit a sharp rise in the temperature dependent ε_r response when the material undergoes a transition from non-centrosymmetric FE state (where the spontaneous polarization exists) to a centrosymmetric paraelectric (PE) state. This transition temperature is called the Curie temperature (T_c). Such transitions in barium titanate perovskite FE will be discussed later. The most studied FE material class is the oxygen octahedral group, also categorized as perovskite ^[9], and we refer further only to this material class in this review. In addition to the recent interests on perovskite-based relaxors for EESSs, which is addressed in this review, this material class has gained interest for various applications such as photovoltaics ^[10][11], catalysis ^[12], smart windows, etc., because of their versatile structure and the possibility to achieve a wide range of electrical, magnetic, optical, and mechanical properties ^[13]. We also caution the reader that non-perovskite systems may also possess high ED properties (for instance, tetragonal tungsten bronzes ^[14][15]) and that the discussion about using additives and novel processing methods may apply to those systems as well.

Perovskite is the classification name given to materials based on the mineral calcium titanate's general crystal structure and bonding arrangement (CaTiO₃) ^[13]. CaTiO3 has the orthorhombic Pbnm crystal structure at room temperature and undergoes reversible phase transformation to tetragonal I4/mcm at ~1240 °C. It transforms to ideal cubic Pm3¯m at a temperature of ~1360 °C and remains Pm3¯m cubic until its melting temperature of ~1975 °C. According to the displacive model, in the ideal cubic perovskite structure (ABO₃), Pm3¯m, (see Figure 3), atoms have a face-centered arrangement, and the structure is cubic close-packed with larger A-site (A) cations and C-site (C) anion forming an FCC lattice with the smaller B-site (B) cation possessing octahedral coordination with anions. This octahedral coordination of the B-site cations classifies perovskites under the oxygen octahedral group. In the perovskite structure, the co-ordination number of A cation is twelve and the B cation and C anion coordination numbers are six each ^[7].

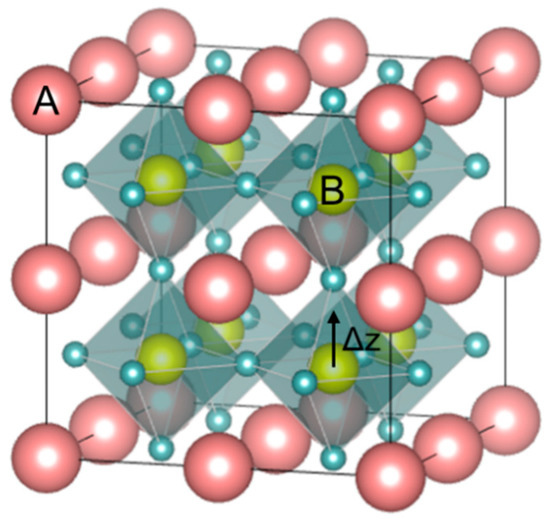
Figure 3. Perovskite ABO₃ structure with the face-centered arrangement. The B cation sits with VI-fold coordination at the center of the oxygen octahedral.

For ferroelectrics and related material systems, the perovskite structure can tolerate a wide range of substitutions in the A and B sites, resulting in significant variations of material properties because of the substitutions changing the polarization energy unit volume, band structure, etc. ^[16][17]. The close-packed perovskite structure's theoretical packing density can range from 0.52 to 0.76 and can be increased further by selective elemental substitution. Each lattice site may incorporate multiple ions of unique ionic radii and valence states that can lead to complex perovskites like PbMg_1/3Nb_2/3O₃ (PMN), Na_1/2Bi_1/2TiO_3, etc. As a result, a perovskite can take on a wide range of crystal structures depending upon the nature of the incorporated atoms, and thus the material rarely forms the ideal cubic perovskite structure. The non-cubic or non-ideal perovskite structure typically transforms into the ideal cubic perovskite structure at elevated temperatures.

Perovskite materials are often structurally understood by applying a semi-empirical relationship known as the Goldschmidt tolerance factor (GTF) ^[18], which is expressed by the following equation,

where R_A, R_B, and R_C are the ionic radii of the A, B, and C-site atom(s), respectively. In Goldschmidt's formalism, T ranges from about 0.77 to about 1.05, with the "ideal" cubic perovskite forming when T is about 1.00. For T > 1, the material is often associated with high permittivity material properties, including ferroelectric materials. For T < 1 is often associated with low symmetry materials. The scientific community has utilized the GTF as a relatively simple tool for nearly a century to guide the discovery and development of new perovskite materials; however, it does not consider effects deviating from pure ionic bonding behavior and thus might not be applicable to all perovskite systems ^[19].

Most of the technologically relevant perovskite materials are based on PbTiO₃, where the A-site of the lattice is occupied by Pb²⁺. The lone electron pair of Pb²⁺ induces a hybridization with the neighboring oxygen anions, thereby shifting the bonding character to covalent. As a result, the Pb²⁺ cation goes off-center, which has important implications in the giant electromechanical properties of PbZr_1-xTi_xO₃ (PZT) and PbMg_1/3Nb_2/3O₃-PbTiO₃ (PMN-PT) solid solutions ^[20]. However, lead-based FE materials are subject of restrictions due to the toxicity of lead-containing compounds, especially during processing steps, and because of the risk of Pb leaking to the environment after end-of-use of electronic components ^[21]. The study of lead-free FE materials is far from being concluded and it is yet unclear how lead-free materials have to be designed to attain desired properties. Thus, the scope of the present work is to review the state-of-the-art of lead-free perovskites, especially for EESSs.

One of the most widely studied lead-free perovskite-based FE materials is barium titanate (BaTiO₃, BTO). Historically, BTO was discovered simultaneously in the United States by Wainer and Salomon in 1942, in Russia by Vul in 1944, and in Japan by Ogawa in 1944. The crystal structure of BTO was first reported by Megaw ^[22] and Von Hippel ^[23]. BTO is an ideal cubic structure above 120–128 °C (Curie temperature-T_c) and follows a Curie–Weiss law:

where C is Curie constant.

Below T_c, BTO undergoes two ferroelectric–ferroelectric phase transitions: a structural phase transformation from tetragonal (space group: P4mm) to orthorhombic (space group: Amm2) at 6–12 °C, followed by a transition from orthorhombic to rhombohedral (space group: R3m) at −77–(−92) °C ^[24]. Figure 4. shows the dielectric and structural properties of BTO ceramics.

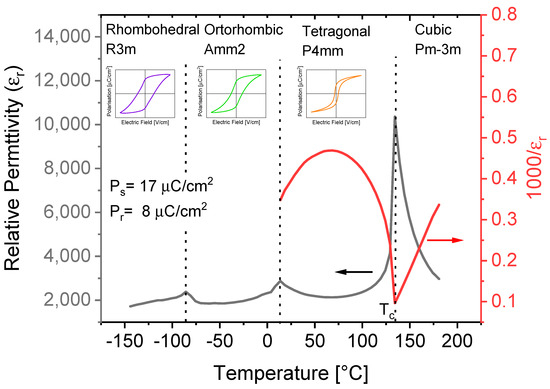
Figure 4. Dielectric and structural properties of BaTiO₃ (BTO) ceramics. Values of saturation polarization (P_s) and remnant polarization (P_r) are at 30 °C.

A chemical modification that includes both chemical substitution and additives is a widespread approach in BTO to enhance or tune the material properties. This modification is later combined with novel fabrication methods for various technological needs ^[25]. In addition to macroscopic material properties, chemical alterations have profound effects on the parent material's fundamental FE nature. Here parent material can be referred to any FE perovskite system that is constituted by one variation of atomic species at every crystallographic site in a perovskite structure without affecting the translational symmetry. Interestingly, chemical alterations, even on an atomic level in an FE parent material, can have a notable impact on the macroscopic properties. From now on, considering the scope of this review, discussions are based primarily on changes observed in macroscopic properties (dielectric properties, PE loops, microstructure, etc.) as a consequence of chemical alterations; however, changes at the atomic scale cannot be completely ignored. Upon chemical alteration, mainly substitutions at a lower concentration level, the lattice continuum of the FE matrix is disrupted, resulting in increased diffusivity of the temperature-dependent ε_r in addition to changes in the well-defined features of the P–E loops that are typical for an FE material. This type of FE material, although chemically modified, retains the long-range FE order and so exhibits a diffuse FE-PE phase transition at the T_c and follows the Curie–Weiss law above T_c. Such FE systems with a broad ε_r response are categorized as FE with ‘diffuse phase transition-DPT' ^[26][27]. The nature of FE phase transitions in DPT is controversial and is outside of the scope of this review. Upon further chemical modification, a peculiar material state, called the ‘relaxor-state', can be achieved. There are three main features that characterize relaxors: (1) A diffuse temperature-dependent relative permittivity response, (2) the dispersion of the relative permittivity maximum as a function of frequency, and (3) the absence of macroscopic symmetry breaking as a function of temperature (the permittivity maximum is hence denoted as T_m instead of T_c). The transition from FE state to a DPT state and finally to a relaxor state is reported in many FE parent materials and this transition sequence is especially valid in BTO based systems ^{[28][29][30][31]}. The compositions between a DPT state and a full relaxor state are generally called "crossover compositions." The exact concentration for this series of composition-driven transitions until the relaxor state varies with different substituting ions and is discussed more in detail in the subsequent sections. This article primarily focuses on BTO-based systems showing relaxor characteristics at high substituent content.

Relaxors are attractive for EESSs because of their relatively high BDS, high ε_r, and slim P–E loops (i.e., low remnant polarization-P_r). Figure 2 depicts the drastic difference in the appearance of the PE loops of relaxors compared to a FE system ^[32]. The slim PE loops are a direct consequence of the chemical heterogeneity that results from chemical modifications, disrupting the long-range polar FE order into a fragmented short-range polar-state ^[33]. The disruptions are of different origin and there are numerous theories available in the literature that differentiate ‘relaxor' states based on the nature of the substituents ^{[34][35][36][37]}. The most recent theory suggests the occurrence of slush-like polar structures, which primarily elucidates the dynamics of electric dipoles as a function of temperature ^[38]. Electric dipoles can originate from static (i.e., defect-induced) and dynamic (cation hopping-induced) lattice disorder. These dipoles are the source of random electric fields (RF) that play a crucial role in inducing relaxor behavior independent of the substitution types. The dynamic disorder is temperature-driven and is not only specific to relaxors but is also present in the cubic phase of BTO, resulting in broad Raman spectra well above the T_c ^[39][40]. The intrinsic static disorder is related to defects and is present even in single-crystal BTO—for example, due to oxygen vacancies ^[41]. It is understood that relaxor behavior might have a different origin in Pb-based or Ba-based systems, since cation off-centering has a role in local lattice polarization.