
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Amir Mosavi | + 8267 word(s) | 8267 | 2018-11-11 21:58:52 | | | |
| 2 | Rita Xu | -421 word(s) | 7846 | 2020-04-29 10:44:51 | | | | |
| 3 | Peter Tang | -78 word(s) | 7768 | 2020-11-01 13:07:01 | | | | |
| 5 | Shaker M. A. Qaidi | + 1 word(s) | 7769 | 2022-12-03 21:11:33 | | |
Video Upload Options
Floods are among the most destructive natural disasters, which are highly complex to model. The research on the advancement of flood prediction models contributed to risk reduction, policy suggestion, minimization of the loss of human life, and reduction of the property damage associated with floods. To mimic the complex mathematical expressions of physical processes of floods, during the past two decades, machine learning (ML) methods contributed highly in the advancement of prediction systems providing better performance and cost-effective solutions. Due to the vast benefits and potential of ML, its popularity dramatically increased among hydrologists.
Researchers through introducing novel ML methods and hybridizing of the existing ones aim at discovering more accurate and efficient prediction models. The main contribution of this paper is to demonstrate the state of the art of ML models in flood prediction and to give insight into the most suitable models. In this paper, the literature where ML models were benchmarked through a qualitative analysis of robustness, accuracy, effectiveness, and speed are particularly investigated to provide an extensive overview on the various ML algorithms used in the field. The performance comparison of ML models presents an in-depth understanding of the different techniques within the framework of a comprehensive evaluation and discussion. As a result, this paper introduces the most promising prediction methods for both long-term and short-term floods. Furthermore, the major trends in improving the quality of flood prediction models are investigated. Among them, hybridization, data decomposition, algorithm ensemble, and model optimization are reported as the most effective strategies for the improvement of ML methods. This survey can be used as a guideline for hydrologists as well as climate scientists in choosing the proper ML method according to the prediction task.
1. Introduction
Among the natural disasters, floods are the most destructive, causing massive damage to human life, infrastructure, agriculture, and the socioeconomic system. Governments, therefore, are under pressure to develop reliable and accurate maps of flood risk areas and further plan for sustainable flood risk management focusing on prevention, protection, and preparedness [1]. Flood prediction models are of significant importance for hazard assessment and extreme event management. Robust and accurate prediction contribute highly to water recourse management strategies, policy suggestions and analysis, and further evacuation modeling [2]. Thus, the importance of advanced systems for short-term and long-term prediction for flood and other hydrological events is strongly emphasized to alleviate damage [3]. However, the prediction of flood lead time and occurrence location is fundamentally complex due to the dynamic nature of climate condition. Therefore, today's major flood prediction models are mainly data-specific and involve various simplified assumptions [4]. Thus, to mimic the complex mathematical expressions of physical processes and basin behavior, such models benefit from specific techniques e.g., event-driven, empirical black box, lumped and distributed, stochastic, deterministic, continuous, and hybrids [5].
Physically based models [6] were long used to predict hydrological events, such as storms [7][8], rainfall/runoff [9][10], shallow water conditions [11], hydraulic models of flow [12][13], and further global circulation phenomena [14], including the coupled effects of atmosphere, ocean, and floods [15]. Although physical models showed great capabilities for predicting a diverse range of flooding scenarios, they often require various types of hydro-geomorphological monitoring datasets, requiring intensive computation, which prohibits short-term prediction [16]. Furthermore, as stated in Reference [17], the development of physically based models often requires in-depth knowledge and expertise regarding hydrological parameters, reported to be highly challenging. Moreover, numerous studies suggest that there is a gap in the short-term prediction capability of physical models (Costabile and Macchione [15]). For instance, on many occasions, such models failed to predict properly [18]. Van den Honert and McAneney [18] documented the failure in the prediction of floods accrued in Queensland, Australia in 2010. Similarly, numerical prediction models [19] were reported in the advancement of deterministic calculations and were not reliable due to systematic errors [20]. Nevertheless, major improvements in physically based models of the flood were recently reported through the hybridization of models [21], as well as advanced flow simulations [22][23].
In addition to numerical and physical models, data-driven models also have a long tradition in flood modeling, which recently gained more popularity. Data-driven methods of prediction assimilate the measured climate indices and hydro-meteorological parameters to provide better insight. Among them, statistical models of autoregressive moving average (ARMA) [24], multiple linear regression (MLR) [25], and autoregressive integrated moving average (ARIMA) [26] are the most common flood frequency analysis (FFA) methods for modeling flood prediction. FFA was among the early statistical methods for predicting floods [27]. Regional flood frequency analyses (RFFA) [28], more advanced versions, were reported to be more efficient when compared to physical models considering computation cost and generalization. Assuming floods as stochastic processes, they can be predicted using certain probability distributions from historical streamflow data [29]. For instance, the climatology average method (CLIM) [28], empirical orthogonal function (EOF) [30], multiple linear regressions (MLR), quantile regression techniques (QRT) [31], and Bayesian forecasting models [32] are widely used for predicting major floods. However, they were reported to be unsuitable for short-term prediction, and, in this context, they need major improvement due to the lack of accuracy, complexity of the usage, computation cost, and robustness of the method. Furthermore, for reliable long-term prediction, at least, a decade of data from measurement gauges should be analyzed for a meaningful forecast [32]. In the absence of such a dataset, however, FFA can be done using hydrologic models of RFFA, e.g., MISBA [33] and Sacramento [34], as reliable empirical methods with regional applications, where streamflow measurements are unavailable. In this context, distributed numerical models are used as an attractive solution [35]. Nonetheless, they do not provide quantitative flood predictions, and their forecast skill level is "only moderate" and they lack accuracy [36].
The drawbacks of the physically based and statistical models mentioned above encourage the usage of advanced data-driven models, e.g., machine learning (ML). A further reason for the popularity of such models is that they can numerically formulate the flood nonlinearity, solely based on historical data without requiring knowledge about the underlying physical processes. Data-driven prediction models using ML are promising tools as they are quicker to develop with minimal inputs. ML is a field of artificial intelligence (AI) used to induce regularities and patterns, providing easier implementation with low computation cost, as well as fast training, validation, testing, and evaluation, with high performance compared to physical models, and relatively less complexity [37]. The continuous advancement of ML methods over the last two decades demonstrated their suitability for flood forecasting with an acceptable rate of outperforming conventional approaches [38]. A recent investigation by Reference [39], which compared performance of a number of physical and ML prediction models, showed a higher accuracy of ML models. Furthermore, the literature includes numerous successful experiments of quantitative precipitation forecasting (QPF) using ML methods for different lead-time predictions [40][41]. In comparison to traditional statistical models, ML models were used for prediction with greater accuracy [42]. Ortiz-García et al. [43] described how ML techniques could efficiently model complex hydrological systems such as floods. Many ML algorithms, e.g., artificial neural networks (ANNs) [44], neuro-fuzzy [45][46], support vector machine (SVM) [47], and support vector regression (SVR) [48][49], were reported as effective for both short-term and long-term flood forecast. In addition, it was shown that the performance of ML could be improved through hybridization with other ML methods, soft computing techniques, numerical simulations, and/or physical models. Such applications provided more robust and efficient models that can effectively learn complex flood systems in an adaptive manner. Although the literature includes numerous evaluation performance analyses of individual ML models [49][50][51][52], there is no definite conclusion reported with regard to which models function better in certain applications. In fact, the literature includes only a limited number of surveys on specific ML methods in specific hydrology fields [53][54][55]. Consequently, there is a research gap for a comprehensive literature review in the general applications of ML in all flood resource variables from the perspective of ML modeling and data-driven prediction systems.
Nonetheless, ML algorithms have important characteristics that need to be carefully taken into consideration. The first is that they are as good as their training, whereby the system learns the target task based on past data. If the data is scarce or does not cover varieties of the task, their learning falls short, and hence, they cannot perform well when they are put into work. Therefore, using robust data enrichment is essential through, e.g., implementing a distribution function of sums of weights [56], invariance assessments to retain the group characteristics [57], or recovering the missing variables using causally dependent coefficients [58].
The second aspect is the capability of each ML algorithm, which may vary across different types of tasks. This can also be called a "generalization problem", which indicates how well the trained system can predict cases it was not trained for, i.e., whether it can predict beyond the range of the training dataset. For example, some algorithms may perform well for short-term predictions, but not for long-term predictions. These characteristics of the algorithms need to be clarified with respect to the type and amount of available training data, and the type of prediction task, e.g., water level and streamflow. In this review, we look into examples of the use of various ML algorithms for various types of tasks. At the abstract level, we decided to divide the target tasks into short-term and long-term prediction. We then reviewed ML applications for flood-related tasks, where we structured ML methods as single methods and hybrid methods. Hybrid methods are those that combine more than one ML method.
Here, we should note that this paper surveys ML models used for predictions of floods on sites where rain gauges or intelligent sensing systems used. Our goal was to survey prediction models with various lead times to floods at a particular site. From this perspective, spatial flood prediction was not involved in this study, as we did not study prediction models used to estimate/identify the location of floods. In fact, we were concerned only with the lead time for an identified site.
2. Method and Outline
This survey identifies the state of the art of ML methods for flood prediction where peer-reviewed articles in top-level subject fields are reviewed. Among the articles identified, through search queries using the search strategy, those including the performance evaluation and comparison of ML methods were given priority to be included in the review to identify the ML methods that perform better in particular applications. Furthermore, to choose an article, four types of quality measure for each article were considered, i.e., source normalized impact per paper (SNIP), CiteScore, SCImago journal rank (SJR), and h-index. The papers were reviewed in terms of flood resource variables, ML methods, prediction type, and the obtained results.
The applications in flood prediction can be classified according to flood resource variables, i.e., water level, river flood, soil moisture, rainfall–discharge, precipitation, river inflow, peak flow, river flow, rainfall–runoff, flash flood, rainfall, streamflow, seasonal stream flow, flood peak discharge, urban flood, plain flood, groundwater level, rainfall stage, flood frequency analysis, flood quantiles, surge level, extreme flow, storm surge, typhoon rainfall, and daily flows [59]. Among these key influencing flood resource variables, rainfall and the spatial examination of the hydrologic cycle had the most remarkable role in runoff and flood modeling [60]. This is the reason why quantitative rainfall prediction, including avalanches, slush flow, and melting snow, is traditionally used for flood prediction, especially in the prediction of flash floods or short-term flood prediction [61]. However, rainfall prediction was shown to be inadequate for accurate flood prediction. For instance, the prediction of streamflow in a long-term flood prediction scenario depends on soil moisture estimates in a catchment, in addition to rainfall [62]. Although, high-resolution precipitation forecasting is essential, other flood resource variables were considered in the [63]. Thus, the methodology of this literature review aims to include the most effective flood resource variables in the search queries.
A combination of these flood resource variables and ML methods was used to implement the complete list of search queries. Note that the ML methods for flood prediction may vary significantly according to the application, dataset, and prediction type. For instance, ML methods used for short-term water level prediction are significantly different from those used for long-term streamflow prediction. Figure 1 represents the organization of the search queries and further describes the survey search methodology.
The search query included three main search terms. The flood resource variables were considered as term 1 of the search (<Flood resource variable1-n>), which included 25 keywords for search queries mentioned above. Term 2 of search (<ML method1-m>) included the ML algorithms. The collection of the references [16][26][28][37][38][42][44] provides a complete list of ML methods, from which the 25 most popular algorithms in engineering applications were used as the keywords of this search. Term 3 included the four search terms most often used in describing flood prediction, i.e., "prediction", "estimation", "forecast", or "analysis". The total search resulted in 6596 articles. Among them, 180 original research papers were refined through our quality measure included in the survey.
Figure 1. Flowchart of the search queries.
Section 3 presents the state of the art of ML in flood prediction. A technical description on the ML method and a brief background in flood applications are provided. Section 4 presents the survey of ML methods used for short-term flood prediction. Section 5 presents the survey of ML methods used for long-term flood prediction. Section 6 presents the conclusions.
3. State of the Art of ML Methods in Flood Prediction
For creating the ML prediction model, the historical records of flood events, in addition to real-time cumulative data of a number of rain gauges or other sensing devices for various return periods, are often used. The sources of the dataset are traditionally rainfall and water level, measured either by ground rain gauges, or relatively new remote-sensing technologies such as satellites, multisensor systems, and/or radars [62]. Nevertheless, remote sensing is an attractive tool for capturing higher-resolution data in real time. In addition, the high resolution of weather radar observations often provides a more reliable dataset compared to rain gauges [63]. Thus, building a prediction model based on a radar rainfall dataset was reported to provide higher accuracy in general [64]. Whether using a radar-based dataset or ground gauges to create a prediction model, the historical dataset of hourly, daily, and/or monthly values is divided into individual sets to construct and evaluate the learning models. To do so, the individual sets of data undergo training, validation, verification, and testing. The principle behind the ML modeling workflow and the strategy for flood modeling are described in detail in the literature [48][65]. Figure 2 represents the basic flow for building an ML model. The major ML algorithms applied to flood prediction include ANNs [66], neuro-fuzzy [67], adaptive neuro-fuzzy inference systems (ANFIS) [68], support vector machines (SVM) [69], wavelet neural networks (WNN) [70], and multilayer perceptron (MLP) [71]. In the following subsections, a brief description and background of these fundamental ML algorithms are presented.
Figure 2. Basic flow for building the machine learning (ML) model.
3.1. Artificial Neural Networks (ANNs)
ANNs are efficient mathematical modeling systems with efficient parallel processing, enabling them to mimic the biological neural network using inter-connected neuron units. Among all ML methods, ANNs are the most popular learning algorithms, known to be versatile and efficient in modeling complex flood processes with a high fault tolerance and accurate approximation [39]. In comparison to traditional statistical models, the ANN approach was used for prediction with greater accuracy [72]. ANN algorithms are the most popular for modeling flood prediction since their first usage in the 1990s [73]. Instead of a catchment's physical characteristics, ANNs derive meaning from historical data. Thus, ANNs are considered as reliable data-driven tools for constructing black-box models of complex and nonlinear relationships of rainfall and flood [74], as well as river flow and discharge forecasting [75]. Furthermore, a number of surveys (e.g., Reference [76]) suggest ANN as one of the most suitable modeling techniques which provide an acceptable generalization ability and speed compared to most conventional models. References [77][78] provided reviews on ANN applications in flood. ANNs were already successfully used for numerous flood prediction applications, e.g., streamflow forecasting [79], river flow [80][81], rainfall–runoff [82], precipitation–runoff modeling [83], water quality [55], evaporation [57], river stage prediction [84], low-flow estimation [85], river flows [86], and river time series [56]. Despite the advantages of ANNs, there are a number drawbacks associated with using ANNs in flood modeling, e.g., network architecture, data handling, and physical interpretation of the modeled system. A major drawback when using ANNs is the relatively low accuracy, the urge to iterate parameter tuning, and the slow response to gradient-based learning processes [87]. Further drawbacks associated with ANNs include precipitation prediction [88][89] and peak-value prediction [90].
The feed-forward neural network (FFNN) [25] is a class of ANN, whereby the network's connections are not in cyclical form. FFNNs are the simplest type of ANN, whereby information moves in a forward direction from input nodes to the hidden layer and later to output nodes. On the other hand, a recurrent neural network (RNN) [91] is a class of ANN, whereby the network's connections form a time sequence for dynamic temporal behavior. Furthermore, RNNs benefit from extra memory to analyze input sequences. In ANNs, backpropagation (BP) is a multi-layered NN where weights are calculated using the propagation of the backward error gradient. In BP, there are more phases in the learning cycle, using a function for activation to send signals to the other nodes. Among various ANNs, the backpropagation ANN (BPNN) was identified as the most powerful prediction tool suitable for flood time-series prediction [26]. Extreme learning machine (ELM) [92] is an easy-to-use form of FFNN, with a single hidden layer. Here, ELM was studied under the scope of ANN methods. ELM for flood prediction recently became of interest for hydrologists and was used to model short-term streamflow with promising results [93][94].
3.2. Multilayer Perceptron (MLP)
The vast majority of ANN models for flood prediction are often trained with a BPNN [95]. While BPNNs are today widely used in this realm, the MLP—an advanced representation of ANNs— recently gained popularity [96]. The MLP [97] is a class of FFNN which utilizes the supervised learning of BP for training the network of interconnected nodes of multiple layers. Simplicity, nonlinear activation, and a high number of layers are characteristics of the MLP. Due to these characteristics, the model was widely used in flood prediction and other complex hydrogeological models [98]. In an assessment of ANN classes used in flood modeling, MLP models were reported to be more efficient with better generalization ability. Nevertheless, the MLP is generally found to be more difficult to optimize [99]. Back-percolation learning algorithms are used to individually calculate the propagation error in hidden network nodes for a more advanced modeling approach.
Here, it is worth mentioning that the MLP, more than any other variation of ANNs (e.g., FFNN, BPNN, and FNN), gained popularity among hydrologists. Furthermore, due to the vast number of case studies using the standard form of MLP, it diverged from regular ANNs. In addition, the authors of articles in the realm of flood prediction using the MLP refer to their models as MLP models. From this perspective, we decided to devote a separate section to the MLP.
3.3. Adaptive Neuro-Fuzzy Inference System (ANFIS)
The fuzzy logic of Zadeh [100] is a qualitative modeling scheme with a soft computing technique using natural language. Fuzzy logic is a simplified mathematical model, which works on incorporating expert knowledge into a fuzzy inference system (FIS). An FIS further mimics human learning through an approximation function with less complexity, which provides great potential for nonlinear modeling of extreme hydrological events [101][102], particularly floods [103]. For instance, Reference [104] studied river level forecasting using an FIS, as did Lohani et al. (2011) [4] for rainfall–runoff modeling for water level. As an advanced form of fuzzy-rule-based modeling, neuro-fuzzy presents a hybrid of the BPNN and the widely used least-square error method [46]. The Takagi–Sugeno (T–S) fuzzy modeling technique [4], which is created using neuro-fuzzy clustering, is also widely applied in RFFA [28].
Adaptive neuro-FIS, or so-called ANFIS, is a more advanced form of neuro-fuzzy based on the T–S FIS, first coined [67][77]. Today, ANFIS is known to be one of the most reliable estimators for complex systems. ANFIS technology, through combining ANN and fuzzy logic, provides higher capability for learning [101]. This hybrid ML method corresponds to a set of advanced fuzzy rules suitable for modeling flood nonlinear functions. An ANFIS works by applying neural learning rules for identifying and tuning the parameters and structure of an FIS. Through ANN training, the ANFIS aims at catching the missing fuzzy rules using the dataset [67]. Due to fast and easy implementation, accurate learning, and strong generalization abilities, ANFIS became very popular in flood modeling. The study of Lafdani et al. [60] further described its capability in modeling short-term rainfall forecasts with high accuracy, using various types of streamflow, rainfall, and precipitation data. Furthermore, the results of Shu and [67] showed easier implementation and better generalization capability, using the one-pass subtractive clustering algorithm, which led several rounds of random selection being avoided.
3.4. Wavelet Neural Network (WNN)
Wavelet transform (WT) [46] is a mathematical tool which can be used to extract information from various data sources by analyzing local variations in time series [50]. In fact, WT has significantly positive effects on modeling performance [105]. Wavelet transforms supports the reliable decomposition of an original time series to improve data quality. The accuracy of prediction is improved through discrete WT (DWT), which decomposes the original data into bands, leading to an improvement of flood prediction lead times [106]. DWT decomposes the initial data set into individual resolution levels for extracting better-quality data for model building. DWTs, due to their beneficial characteristics, are widely used in flood time-series prediction. In flood modeling, DWTs were widely applied in, e.g., rainfall–runoff [51], daily streamflow [106], and reservoir inflow [107]. Furthermore, hybrid models of DWTs, e.g., wavelet-based neural networks (WNNs) [108], which combine WT and FFNNs, and wavelet-based regression models [109], which integrate WT and multiple linear regression (MLR), were used in time-series predictions of floods [110]. The application of WNN for flood prediction was reviewed in Reference [70], where it was concluded that WNNs can highly enhance model accuracy. In fact, most recently, WNNs, due to their potential in enhancing time-series data, gained popularity in flood modeling [50], for applications such as daily flow [111], rainfall–runoff [112], water level [113], and flash floods [114].
3.5. Support Vector Machine (SVM)
Hearst et al. [115] proposed and classified the support vector (SV) as a nonlinear search algorithm using statistical learning theory. Later, the SVM [116] was introduced as a class of SV, used to minimize over-fitting and reduce the expected error of learning machines. SVM is greatly popular in flood modeling; it is a supervised learning machine which works based on the statistical learning theory and the structural risk minimization rule. The training algorithm of SVM builds models that assign new non-probabilistic binary linear classifiers, which minimize the empirical classification error and maximize the geometric margin via inverse problem solving. SVM is used to predict a quantity forward in time based on training from past data. Over the past two decades, the SVM was also extended as a regression tool, known as support vector regression (SVR) [117].
SVMs are today know as robust and efficient ML algorithms for flood prediction [118]. SVM and SVR emerged as alternative ML methods to ANNs, with high popularity among hydrologists for flood prediction. They use the statistical learning theory of structural risk minimization (SRM), which provides a unique architecture for delivering great generalization and superior efficiency. Most importantly, SVMs are both suitable for linear and nonlinear classification, and the efficient mapping of inputs into feature spaces [119]. Thus, they were applied in numerous flood prediction cases with promising results, excellent generalization ability, and better performance, compared to ANNs and MLRs, e.g., extreme rainfall [120], precipitation [43], rainfall–runoff [121], reservoir inflow [122], streamflow [123], flood quantiles [48], flood time series [124], and soil moisture [125]. Unlike ANNs, SVMs are more suitable for nonlinear regression problems, to identify the global optimal solution in flood models [126]. Although the high computation cost of using SVMs and their unrealistic outputs might be demanding, due to their heuristic and semi-black-box nature, the least-square support vector machine (LS-SVM) highly improved performance with acceptable computational efficiency [127]. The alternative approach of LS-SVM involves solving a set of linear tasks instead of complex quadratic problems [128]. Nevertheless, there are still a number of drawbacks that exist, especially in the application of seasonal flow prediction using LS-SVM [129].
3.6. Decision Tree (DT)
The ML method of DT is one of the contributors in predictive modeling with a wide application in flood simulation. DT uses a tree of decisions from branches to the target values of leaves. In classification trees (CT), the final variables in a DT contain a discrete set of values where leaves represent class labels and branches represent conjunctions of features labels. When the target variable in a DT has continuous values and an ensemble of trees is involved, it is called a regression tree (RT) [130]. Regression and classification trees share some similarities and differences. As DTs are classified as fast algorithms, they became very popular in ensemble forms to model and predict floods [131]. The classification and regression tree (CART) [132][133], which is a popular type of DT used in ML, was successfully applied to flood modeling; however, its applicability to flood prediction is yet to be fully investigated [134]. The random forests (RF) method [69][135] is another popular DT method for flood prediction [136]. RF includes a number of tree predictors. Each individual tree creates a set of response predictor values associated with a set of independent values. Furthermore, an ensemble of these trees selects the best choice of classes [69]. Reference [137] introduced RF as an effective alternative to SVM, which often delivers higher performance in flood prediction modeling. Later, Bui et al. [138] compared the performances of ANN, SVM, and RF in general applications to floods, whereby RF delivered the best performance. Another major DT is the M5 decision-tree algorithm [139]. M5 constructs a DT by splitting the decision space and single attributes, thereby decreasing the variance of the final variable. Further DT algorithms popular in flood prediction include reduced-error pruning trees (REPTs), Naïve Bayes trees (NBTs), chi-squared automatic interaction detectors (CHAIDs), logistic model trees (LMTs), alternating decision trees (ADTs), and exhaustive CHAIDs (E-CHAIDs).
3.7. Ensemble Prediction Systems (EPSs)
A multitude of ML modeling options were introduced for flood modeling with a strong background [140]. Thus, there is an emerging strategy to shift from a single model of prediction to an ensemble of models suitable for a specific application, cost, and dataset. ML ensembles consist of a finite set of alternative models, which typically allow more flexibility than the alternatives. Ensemble ML methods have a long tradition in flood prediction. In recent years, ensemble prediction systems (EPSs) [141] were proposed as efficient prediction systems to provide an ensemble of N forecasts. In EPS, N is the number of independent realizations of a model probability distribution. EPS models generally use multiple ML algorithms to provide higher performance using an automated assessment and weighting system [140]. Such a weighting procedure is carried out to accelerate the performance evaluation process. The advantage of EPS is the timely and automated management and performance evaluation of the ensemble algorithms. Therefore, the performance of EPS, for flood modeling in particular, can be improved. EPSs may use multiple fast-learning or statistical algorithms as classifier ensembles, e.g., ANNs, MLP, DTs, rotation forest (RF) bootstrap, and boosting, allowing higher accuracy and robustness. The subsequent ensemble prediction systems can be used to quantify the probability of floods, based on the prediction rate used in the event [142][143][144]. Therefore, the quality of ML ensembles can be calculated based on the verification of probability distribution. Ouyang et al [145] and Zhang et al. [146] presented a review of the applications of ensemble ML methods used for floods. EPSs were demonstrated to have the capability for improving model accuracy in flood modeling [140][141][142][143][144][145][146].
To improve the accuracy of import data and to achieve better dataset management, the ensemble mean was proposed as a powerful approach coupled with ML methods [140][141]. Empirical mode decomposition (EMD) [142], and ensemble EMD (EEMD) [143] are widely used for flood prediction [144]. Nevertheless, EMD-based forecast models are also subject to a number of drawbacks [145]. The literature includes numerous studies on improving the performance of decomposition and prediction models in terms of additivity and generalization ability [146].
3.8. Classification of ML Methods and Applications
The most popular ML modeling methods for flood prediction were identified in the previous section, including ANFIS, MLP, WNN, EPS, DT, RF, CART, and ANN. Figure 3 presents the major ML methods used for flood prediction, and the number of corresponding articles in the literature over the last decade. This figure was designed to communicate to the readers which ML methods increased in popularity among hydrologists for flood modeling within the past decade.
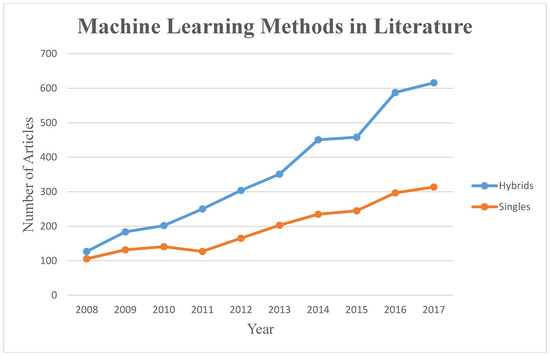
Figure 3. Major ML methods used for flood prediction in the literature. Reference year: 2008 (source: Scopus).
Considering the ML methods for application to floods, it is apparent that ANNs, SVMs, MLPs, DTs, ANFIS, WNNs, and EPSs are the most popular. These ML methods can be categorized as single and hybrid methods. In addition to the fundamental hybrid ML methods, i.e., ANFIS, WNNs, and basic EPSs, several different research strategies for obtaining better prediction evolved [137]. The strategies involved developing hybrid ML models using soft computing techniques, statistical methods, and physical models rather than individual ML approaches, whereby the extra components complement each other with respect to their drawbacks and shortcomings. The success of such hybrid approaches motivated the research community to explore more advanced hybrid models. Figure 4 presents the progress of single vs. hybrid ML methods for flood prediction in the literature over the past decade. The figure shows an apparent continuous increase and notable progress in using novel hybrid methods. Through Figure 4, the taxonomy of our research was justified, based on distinguishing hybrid and single ML prediction models.

Figure 4. The progress of single vs. hybrid ML methods for flood prediction in the literature. Reference year: 2008 (source: Scopus).
Furthermore, the types of prediction are often studied with different lead-time predictions due to the flood. Real-time, hourly, daily, weekly, monthly, seasonal, annual, short-term, and long-term are the terms most often used in the literature. Real-time prediction is concerned with anywhere between few minutes and an hour preceding the flood. Hourly predictions can be 1–3 h ahead of the flood forecasting lead time or, in some cases, 18 h or 24 h. Daily predictions can be 1–6 days ahead of the forecast. Monthly forecasts can be, for instance, up to three months. In hydrology, the definitions of short-term and long-term in studying the different phenomena vary. Short-term predictions for floods often refer to hourly, daily, and weekly predictions, and they are used as warning systems. On the other hand, long-term predictions are mostly used for policy analysis purposes. Furthermore, if the prediction leading time to flood is three days longer than the confluence time, the prediction is considered to be long-term [37][58]. From this perspective, in this study, we considered a lead time greater than a week as a long-term prediction. It was observed that the characteristics of the ML methods used varied significantly according to the period of prediction. Thus, dividing the survey on the basis of short-term and long-term was essential.
Here, it is also worth emphasizing that, in this paper, the prediction lead-time was classified as "short-term" or "long-term". Although flash floods happen in a short period of time with great destructive power, they can be predicted with either "short-term" or "long-term" lead times to the actual flood. In fact, this paper is concerned with the lead times instead of the duration or type of flood. If the lead-time prediction to a flash flood was short-term, then it was studied as a short-term lead time. However, sometimes flash floods can be predicted with long lead times. In other words, flash floods might be predicted one month ahead. In this case, the prediction was considered as long-term. Regardless of the type of flood, we only focused on the lead time.
In this study, the ML methods were reviewed using two classes—single methods and hybrid methods. Figures 5 and 6 represent the taxonomy of the research.
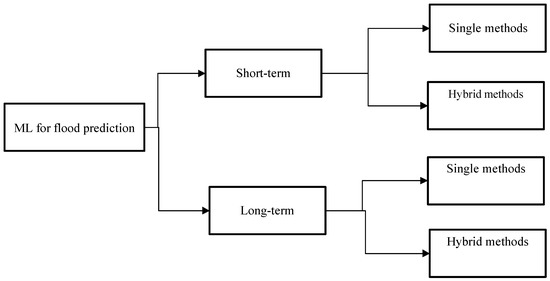
Figure 5. Taxonomy of the survey—ML methods for flood prediction.
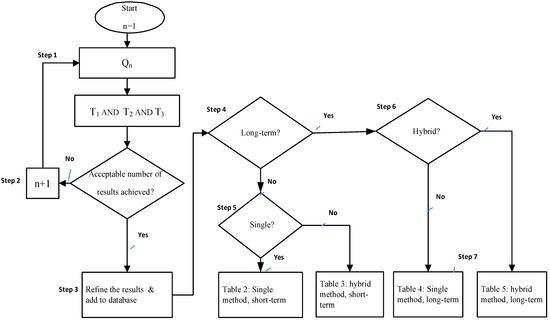
Figure 6. Taxonomy of the survey.
Step 1 involved running the queries one by one; step 2 involved checking the results of the search, and initiating the next search; step 3 involved identifying the comparative studies on ML models of prediction, refining the results and building the database; step 4 involved identifying whether it was a long-term or short-term prediction; steps 5 and 6 involved identifying if it was a single or hybrid method, constructing Table 1, and step 7 involved constructing the other Tables. The four tables provide the list of studies on different prediction techniques, which entail the organized comprehensive surveys of the literature.
4. Short-Term Flood Prediction with ML
Short-term lead-time flood predictions are considered important research challenges, particularly in highly urbanized areas, for timely warnings to residences so to reduce damage [146]. In addition, short-term predictions contribute highly to water recourse management. Even with the recent improvements in numerical weather prediction (NWP) models, artificial intelligence (AI) methods, and ML, short-term prediction remains a challenging task [147][148][149][150][151][152]. This section is divided into two subsections—single and hybrid methods of ML—to individually investigate each group of methods.
4.1. Short-Term Flood Prediction Using Single ML Methods
To gain insight into the performance of ML methods, a comprehensive comparison was required to investigate ML methods. Table 1 presents a summary of the major ML methods, i.e., ANNs, MLP, nonlinear autoregressive network with exogenous inputs (NARX), M5 model trees, DTs, CART, SVR, and RF, followed by a comprehensive performance comparison of single ML methods in short-term flood prediction. A revision and discussion of these methods follow so as to identify the most suitable methods presented in the literature.
Table 1. Short-term predictions using single machine learning (ML) methods.
|
Modeling Technique |
Reference |
Flood Resource Variable |
Prediction Type |
Region |
|
ANN vs. statistical |
[1] |
Streamflow and flash food |
Hourly |
USA |
|
ANN vs. traditional |
[44] |
Water and surge level |
Hourly |
Japan |
|
ANN vs. statistical |
[149] |
Flood |
Real-time |
UK |
|
ANN vs. statistical |
[150] |
Extreme flow |
Hourly |
Greece |
|
FFANN vs. ANN |
[151] |
Water level |
Hourly |
India |
|
ANN vs. T–S |
[4] |
Flood |
Hourly |
India |
|
ANN vs. AR |
[153] |
Stage level and streamflow |
Hourly |
Brazil |
|
MLP vs. Kohonen NN |
[154] |
Flood frequency analysis |
Long-term |
China |
|
BPANN |
[155] |
Peak flow of flood |
Daily |
Canada |
|
BPANN vs. DBPANN |
[156] |
Rainfall–runoff |
Monthly and daily |
China |
|
BPANN |
[157] |
Flash flood |
Real-time |
Hawaii |
|
BPANN |
[158] |
Runoff |
Daily |
India |
|
ELM vs. SVM |
[159] |
Streamflow |
Daily |
China |
|
BPANN vs. NARX |
Urban flood |
Real-time |
Taiwan |
|
|
FFANN vs. Functional ANN |
[162] |
River flows |
Real-time |
Ireland |
|
Recurrent NN vs. Z–R relation |
[163] |
Rainfall prediction |
Real-time |
Taiwan |
|
ANN vs. M5 model tree |
[164] |
Peak flow |
Hourly |
India |
|
NBT vs. DT vs. Multinomial regression |
[165] |
Flash flood |
Real-time, hourly |
Austria |
|
DTs vs. NBT vs. ADT vs. LMT, and REPT |
[166] |
Flood |
Hourly/daily |
Iran |
|
MLP vs. MLR |
River flow and rainfall–runoff |
Daily |
Algeria |
|
|
MLP vs. MLR |
[98] |
River runoff |
Hourly |
Morocco |
|
MLP vs. WT vs. MLR vs. ANN |
[169] |
River flood forecasting |
Daily |
Canada |
|
ANN vs. MLP |
[170] |
River level |
Hourly |
Ireland |
|
MLP vs. DT vs. CART vs. CHAID |
[171] |
Flood during typhoon |
Rainfall–runoff |
China |
|
SVM vs. ANN |
[120] |
Rainfall extreme events |
Daily |
India |
|
ANN vs. SVR |
[48] |
Flood |
Daily |
Canada |
|
RF vs. SVM |
[69] |
Rainfall |
Hourly |
Taiwan |
Kim and Barros [148] modified an ANN model to improve flood forecasting short-term lead time through consideration of atmospheric conditions. They used satellite data from the ISCCP-B3 dataset [172]. This dataset includes hourly rainfall from 160 rain gauges within the region. The ANN was reported to be considerably more accurate than the statistical models. In another similar work, Reference [44] developed an ANN forecast model for hourly lead time. In their study, various datasets were used, consisting of meteorological and hydrodynamic parameters of three typhoons. Testing of the ANN forecast models showed promising results for 5-h lead time. In another attempt, Danso-Amoako [1] provided a rapid system for predicting floods with an ANN. They provided a reliable forecasting tool for rapidly assessing floods. An value of 0.70 for the ANN model proved that the tool was suitable for predicting flood variables with a high generalization ability. The results of [149] provides similar conclusions. Furthermore, Panda, Pramanik, and Bala [151] compared the accuracy of ANN with FFANN, and the results were benchmarked with the physical model of MIKE 11 for short-term water level prediction. This dataset includes the hourly discharge and water level between 2006 and 2009. The data of the year 2006 was used for testing root-mean-square error (RMSE). The results indicated that the FFANN performed faster and relatively more accurately than the ANN model. Here, it is worth mentioning that the overall results indicated that the neural networks were superior compared to the one-dimensional model MIKE 11. Nevertheless, there were great advancements reported in the implementation of two-dimensional MIKE 11 [8].
Kourgialas, Dokou, and Karatzas [150] created a modeling system for the prediction of extreme flow based on ANNs 3 h, 12 h, and 19 h ahead of the flood. They analyzed five years of hourly data to investigate the ANN effectiveness in modeling extreme flood events. The results indicated it to be highly effective compared to conventional hydrological models. Lohani, Goel, and Bhatia [4] improved the real-time forecasting of rainfall–runoff of foods, and the results were compared to the T–S fuzzy model and the subtractive-clustering-based T–S (TSC-T–S) fuzzy model. They, however, concluded that the fuzzy model provided more accurate predictions with longer lead time. The hourly rainfall data from 1989 to 1995 of a gauge site, in addition to the rainfall during a monsoon, was used. Pereira Filho and dos Santos [153] compared the AR model with an ANN in simulating forecast stage level and streamflow. The dataset was created from independent flood events, radar-derived rainfall, and streamflow rain gauges available between 1991 and 1995. The AR and ANN were employed to model short-term flood in an urban area utilizing streamflow and weather data. They showed that the ANN performed better in its verification and it was proposed as a better alternative to the AR model.
Ahmad and Simonovic [155] used a BPNN for predicting peak flow utilizing causal meteorological parameters. This dataset included daily discharge data for 1958–1997 from gauging stations. BPNN proved to be a fast and accurate approach with the ability of generalization for application to other locations with similar rivers. Furthermore, to improve the simulation of daily streamflow using BPNN, Reference [156] used division-based backpropagation to obtain satisfying results. The raw data of local evaporation and rainfall gauges of six years were used for the short-term flood prediction of a streamflow time series. The dataset of one decade from 1988 was used for training and the dataset of five subsequent years was used for testing. The BPNN model provided promising results; however, it lacked efficiency in using raw data for the time-series prediction of streamflow. In addition, Reference [157] showed the application of BPNN for assessing flash floods using measured data. This dataset included 5-min-frequency water quality data and 15-min-frequency rainfall data of 20 years from two rain gauge stations. Their experiments introduced ANN models as simple ML methods to apply, while simultaneously requiring expert knowledge by the user. In addition, their ANN prediction model showed great ability to deal with a noisy dataset. Ghose [158] predicted the daily runoff using a BPNN prediction model. The data of daily water level of two years from 2013–2015 were used. The accurate BPNN model was reported with an efficiency of 96.4% and an R2 of 0.94 for flood prediction.
Pan, Cheng, and Cai [159] compared the performances of ELM and SVM for short-term streamflow prediction. Both methods demonstrated a similar level of accuracy. However, ELM was suggested as a faster method for parameter selection and learning loops. Reference [154] also conducted a comparison between fuzzy c-means, ANN, and MLP using a common dataset of sites to investigate ML method efficiency and accuracy. The MLP and ANN methods were proposed as the best methods. Chang, Chen, Lu, Huang, and Chang [160] and Reference [161] modeled multi-step urban flood forecasts using BPNN and a nonlinear autoregressive network with exogenous input (NARX) for hourly forecasts. The results demonstrated that NARX worked better in short-term lead-time prediction compared to BPNN. The NARX network produced an average R2 value of 0.7. This study suggested that the NARX model was effective in urban flood prediction. Furthermore, Valipour et al. [24] showed how the accuracy of ANN models could be increased through integration with autoregressive (AR) models.
Bruen and Yang [162] modeled real-time rainfall–runoff forecasting for different lead times using FFNN, ARMA, and functional networks. Here, functional networks [173] were compared with an FFNN model. The models were tested using a storm time-series dataset. The result was that functional networks allowed quicker training in the prediction of rainfall–runoff processes with different lead times. The models were able to predict floods with short lead times. Reference [164] estimated water level–discharge using M5 trees and ANN. This dataset was collected from the period of 1990 to 1998, and the inputs were supplied by computing the average mutual information. The ANN and M5 model tree performed similar in terms of accuracy. Reference [166] tested four DT models, i.e., alternating decision trees (ADTs), reduced-error pruning trees (REPTs), logistic model trees (LMTs), and NBTs, using a dataset of 200 floods. The ADT model was reported to perform better for flash-flood prediction for a speedy determination of flood-susceptible areas. In other research, Reference [165] compared the performance of an NBT and DT prediction model, using geomorphological disposition parameters. Both models and their hybrids were compared in terms of prediction accuracy in a catchment. The advanced DTs were found to be promising for flood assessment in prone areas. They concluded that an independent dataset and benchmarking of other ML methods were required for judgment of the accuracy and efficiency of the method. Reference [171] worked on a dataset including more than 100 tropical cyclones (TCs) affecting a watershed for the hourly prediction of precipitation. The performances of MLP, CART, CHAID, exhaustive CHAID, MLR, and CLIM were compared. The evaluation results showed that MLP and DTs provided better prediction. Reference [163] applied a dynamic ANN, as well as a Z–R relation approach for constructing a one-hour-ahead prediction model. This dataset included three-dimensional radar data of typhoon events and rain gauges from 1990 to 2004, including various typhoons. The results indicated that the ANN performed better.
Aichouri, Hani, Bougherira, Djabri, Chaffai, and Lallahem [167] implemented an MLP model for flood prediction, and compared the results with the traditional MLR model. The rainfall–runoff daily data from 1986 to 2003 were used for model building. The results and comparative study indicated that the MLP approach performed with better yield for river rainfall–runoff. In a similar research, Reference [98] modeled and predicted the river rainfall–runoff relationship through training six years of collected daily rainfall data using MLP and MLR (1990 to 1995). Furthermore, the data of 1996 were used for testing to select the best performing network model. The R2 values for the ANN and MLR models were 0.888 and 0.917, respectively, showing that the MLP approach gave a much better prediction than MLR. Reference [169] proposed a number of data-based flood predictions for daily stream flows models using MLP, WT, MLR, ARIMA, and ANN. This dataset included two time series of streamflow and a meteorological dataset including records from 1970 to 2001. The results showed that MLP, WT, and ANN performed generally better. However, the proposed WT prediction model was evaluated to be not as accurate as ANN and MLP for a one-week lead time. Reference [170] designed optimal models of ANN and MLP for the prediction of river level. This study indicated that an optimization tool for the ANN network can highly improve prediction quality. The candidate inputs included river levels and mean sea-level pressure (SLP) for the period of 2001–2002. The MLP was identified as the most accurate model for short-term river flood prediction.
Nayak and Ghosh [120] used SVM and ANN to predict hourly rainfall–runoff using weather patterns. A model of SVM classifier for rainfall prediction was used and the results were compared to ANN and another advanced statistical technique. The SVM model appeared to predict extreme floods better than the ANN. Furthermore, the SVM model proved to function better in terms of uncertainty. Gizaw and Gan [48] developed SVR and ANN models for creating RFFA to estimate regional flood quantiles and to assess climate change impact. This dataset included daily precipitation data obtained from gauges from 1950 to 2016. RMSE and R2 were used for the evaluation of the models. The SVR model estimated regional flood more accurately than the ANN model. SVR was reported to be a suitable choice for predicting future flood under the uncertainty of climate change scenarios [118]. In a similar attempt, Reference [69] provided effective real-time flood prediction using a rainfall dataset measured by radar. Two models of RF and SVM were developed and their prediction performances were compared. Their performance comparison revealed the effectiveness of SVM in real-time flood forecasting.
Table 2 represents a comparative analysis of single ML models for the prediction of short-term floods, considering the complexity of the algorithm, ease of use, running speed, accuracy, and input dataset. This table was created based on the revisions that were made on the articles of Table 1 and also the accuracy analysis of Figure 3, where the values of R2 and RMSE of the single ML methods were considered. The quality of ML model prediction, in terms of speed, complexity, accuracy, and ease of use, was continuously improved through using ensembles of ML methods, hybridization of ML methods, optimization algorithms, and/or soft computing techniques. This trend of improvement is discussed in detail in the discussion.
Table 2. Comparative analysis of single ML models for the prediction of short-term floods.
|
Modeling Technique |
Complexity of Algorithm |
Ease of Use |
Speed |
Accuracy |
Input Dataset |
|
ANN |
High |
Low |
Fair |
Fair |
Historical |
|
BPANN |
Fairly high |
Low |
Fairly high |
Fairly high |
Historical |
|
MLP |
Fairly high |
Fair |
High |
Fairly high |
Historical |
|
ELM |
Fair |
Fairly high |
Fairly high |
Fair |
Historical |
|
CART |
Fair |
Fair |
Fair |
Fairly high |
Historical |
|
SVM |
Fairly high |
Low |
Low |
Fair |
Historical |
|
ANFIS |
Fair |
Fairly high |
Fair |
Fairly high |
Historical |
4.2. Short-Term Flood Prediction Using Hybrid ML Methods
To improve the quality of prediction, in terms of accuracy, generalization, uncertainty, longer lead time, speed, and computation costs, there is an ever increasing trend in building hybrid ML methods. These hybrid methods are numerous, including more popular ones, such as ANFIS and WNN, and further novel algorithms, e.g., SVM–FR, HEC–HMS–ANN, SAS–MP, SOM–R-NARX, wavelet-based NARX, WBANN, WNN–BB, RNN–SVR, RSVRCPSO, MLR–ANN, FFRM–ANN, and EPSs. Table 3 presents these methods; a revision of the methods and applications follows along with a discussion on the ML methods.
Table 3. Short-term flood prediction using hybrid ML methods.
|
Modeling Technique |
Reference |
Flood resource Variable |
Prediction Type |
Region |
|
ANFIS vs. ANN |
[174] |
Flash floods |
Real-time |
Spain |
|
ANFIS vs. ANN |
Water level |
Hourly |
Taiwan |
|
|
ANFIS vs. ANN |
[46] |
Watershed rainfall |
Hourly |
Taiwan |
|
ANFIS vs. ANN |
[67] |
Flood quantiles |
Real-time |
Canada |
|
ANN vs. ANFIS |
[177] |
Daily flow |
Daily |
Iran |
|
CART vs. ANFIS vs. MLP vs. SVM |
[134] |
Sediment transport |
Daily |
Iran |
|
MLP vs. GRNNM vs. NNM |
[96] |
Flood prediction |
Daily |
Korea |
|
SVM-FR vs. DT |
[178] |
Rainfall–runo |
References
- Ebenezer Danso-Amoako; Miklas Scholz; Nickolas Kalimeris; Qinli Yang; Junming Shao; Predicting dam failure risk for sustainable flood retention basins: A generic case study for the wider Greater Manchester area. Computers, Environment and Urban Systems 2012, 36, 423-433, 10.1016/j.compenvurbsys.2012.02.003.
- Kun Xie; Kaan Ozbay; Yuan Zhu; Hong Yang; Evacuation Zone Modeling under Climate Change: A Data-Driven Method. Journal of Infrastructure Systems 2017, 23, 04017013, 10.1061/(asce)is.1943-555x.0000369.
- Pitt, M. Learning Lessons from the 2007 Floods; Cabinet Office: London, UK, 2008.
- Anil Kumar Lohani; N.K. Goel; K.K.S. Bhatia; Improving real time flood forecasting using fuzzy inference system. Journal of Hydrology 2014, 509, 25-41, 10.1016/j.jhydrol.2013.11.021.
- Mosavi, A.; Bathla, Y.; Varkonyi-Koczy, A. Predicting the Future Using Web Knowledge: State of the Art Survey. In Recent Advances in Technology Research and Education; Springer: Cham, Switzerland, 2017; pp. 341–349.
- Mei Zhao; Harry H. Hendon; Representation and prediction of the Indian Ocean dipole in the POAMA seasonal forecast model. Quarterly Journal of the Royal Meteorological Society 2009, 135, 337-352, 10.1002/qj.370.
- Deva K. Borah; Hydrologic procedures of storm event watershed models: a comprehensive review and comparison. Hydrological Processes 2011, 25, 3472-3489, 10.1002/hyp.8075.
- Pierfranco Costabile; Carmelina Costanzo; Francesco Macchione; A storm event watershed model for surface runoff based on 2D fully dynamic wave equations. Hydrological Processes 2013, 27, 554-569, 10.1002/hyp.9237.
- Luís Cea; M. Garrido; Jerónimo Puertas; Experimental validation of two-dimensional depth-averaged models for forecasting rainfall–runoff from precipitation data in urban areas. Journal of Hydrology 2010, 382, 88-102, 10.1016/j.jhydrol.2009.12.020.
- Javier Fernández Pato; Daniel Caviedes-Voullième; Pilar García-Navarro; Rainfall/runoff simulation with 2D full shallow water equations: Sensitivity analysis and calibration of infiltration parameters. Journal of Hydrology 2016, 536, 496-513, 10.1016/j.jhydrol.2016.03.021.
- Daniel Caviedes-Voullième; Pilar García-Navarro; Javier Murillo; Influence of mesh structure on 2D full shallow water equations and SCS Curve Number simulation of rainfall/runoff events. Journal of Hydrology 2012, 448, 39-59, 10.1016/j.jhydrol.2012.04.006.
- Pierfranco Costabile; Carmelina Costanzo; Francesco Macchione; Comparative analysis of overland flow models using finite volume schemes. Journal of Hydroinformatics 2012, 14, 122-135, 10.2166/hydro.2011.077.
- Xilin Xia; Qiuhua Liang; Xiaodong Ming; Jingming Hou; An efficient and stable hydrodynamic model with novel source term discretization schemes for overland flow and flood simulations. Water Resources Research 2017, 53, 3730-3759, 10.1002/2016wr020055.
- Xu Liang; Dennis P. Lettenmaier; Eric F. Wood; Stephen J. Burges; A simple hydrologically based model of land surface water and energy fluxes for general circulation models. Journal of Geophysical Research 1994, 99, 14415, 10.1029/94jd00483.
- Pierfranco Costabile; Francesco Macchione; Enhancing river model set-up for 2-D dynamic flood modelling. Environmental Modelling & Software 2015, 67, 89-107, 10.1016/j.envsoft.2015.01.009.
- Nayak, P.; Sudheer, K.; Rangan, D.; Ramasastri, K. Short-term flood forecasting with a neurofuzzy model. Water Resour. Res. 2005, 41.
- Byunghyun Kim; Brett F. Sanders; James Famiglietti; Vincent Guinot; Urban flood modeling with porous shallow-water equations: A case study of model errors in the presence of anisotropic porosity. Journal of Hydrology 2015, 523, 680-692, 10.1016/j.jhydrol.2015.01.059.
- Robin Van Den Honert; John McAneney; The 2011 Brisbane Floods: Causes, Impacts and Implications. Water 2011, 3, 1149-1173, 10.3390/w3041149.
- Tim H. Lee; Konstantine P. Georgakakos; Operational Rainfall Prediction on Meso-γ Scales for Hydrologic Applications. Water Resources Research 1996, 32, 987-1003, 10.1029/95wr03814.
- Durga Shrestha; David Robertson; Quan Wang; T.C. Pagano; H. A. P. Hapuarachchi; Evaluation of numerical weather prediction model precipitation forecasts for short-term streamflow forecasting purpose. Hydrology and Earth System Sciences 2013, 17, 1913-1931, 10.5194/hess-17-1913-2013.
- Vasilis Bellos; George Tsakiris; A hybrid method for flood simulation in small catchments combining hydrodynamic and hydrological techniques. Journal of Hydrology 2016, 540, 331-339, 10.1016/j.jhydrol.2016.06.040.
- B. Bout; V.G. Jetten; The validity of flow approximations when simulating catchment-integrated flash floods. Journal of Hydrology 2018, 556, 674-688, 10.1016/j.jhydrol.2017.11.033.
- Costabile, P.; Macchione, F.; Natale, L.; Petaccia, G; Flood mapping using lidar dem. Limitations of the 1-D modeling highlighted by the 2-D approach. Nat. Hazards 2015, 77, 181–204.
- Perlaza Samir; Mohammad Valipour; Mohammad Ebrahim Banihabib; Seyyed Mahmood Reza Behbahani; Parameters Estimate of Autoregressive Moving Average and Autoregressive Integrated Moving Average Models and Compare Their Ability for Inflow Forecasting. Journal of Mathematics and Statistics 2012, 8, 330-338, 10.3844/jmssp.2012.330.338.
- Adamowski, J.; Fung Chan, H.; Prasher, S.O.; Ozga-Zielinski, B.; Sliusarieva, A. Comparison of multiple linear and nonlinear regression, autoregressive integrated moving average, artificial neural network, and wavelet artificial neural network methods for urban water demand forecasting in montreal, Canada. Water Resour. Res. 2012, 48.
- Mohammad Valipour; Mohammad Ebrahim Banihabib; Seyyed Mahmood Reza Behbahani; Comparison of the ARMA, ARIMA, and the autoregressive artificial neural network models in forecasting the monthly inflow of Dez dam reservoir. Journal of Hydrology 2013, 476, 433-441, 10.1016/j.jhydrol.2012.11.017.
- Chow, V.T.; Maidment, D.R.; Larry, W. Mays. Applied hydrology; International Edition; MacGraw-Hill, Inc.: New York, NY, USA, 1988; p. 149.
- K. Aziz; Ataur Rahman; G. Fang; S. Shrestha; Application of artificial neural networks in regional flood frequency analysis: a case study for Australia. Stochastic Environmental Research and Risk Assessment 2014, 28, 541-554, 10.1007/s00477-013-0771-5.
- Charles Kroll; Richard M. Vogel; Probability Distribution of Low Streamflow Series in the United States. Journal of Hydrologic Engineering 2002, 7, 137-146, 10.1061/(asce)1084-0699(2002)7:2(137).
- Tomoki Ushiyama; Takahiro Sayama; Yoichi Iwami; Ensemble Flood Forecasting of Typhoons Talas and Roke at Hiyoshi Dam Basin. Journal of Disaster Research 2016, 11, 1032-1039, 10.20965/jdr.2016.p1032.
- Khaled Haddad; Ataur Rahman; Regional flood frequency analysis in eastern Australia: Bayesian GLS regression-based methods within fixed region and ROI framework – Quantile Regression vs. Parameter Regression Technique. Journal of Hydrology 2012, 430, 142-161, 10.1016/j.jhydrol.2012.02.012.
- Thompson, S.A. Hydrology for Water Management; CRC Press: Boca Raton, FL, USA, 2017.
- Ernst Kerkhoven; Thian Yew Gan; A modified ISBA surface scheme for modeling the hydrology of Athabasca River Basin with GCM-scale data. Advances in Water Resources 2006, 29, 808-826, 10.1016/j.advwatres.2005.07.016.
- Burnash, R.J.; Ferral, R.L.; McGuire, R.A. A Generalized Streamflow Simulation System, Conceptual Modeling for Digital Computers; Stanford University: Stanford, CA, USA, 1973.
- Yamazaki, D.; Kanae, S.; Kim, H.; Oki, T. A physically based description of floodplain inundation dynamics in a global river routing model. Water Resour. Res. 2011, 47.
- R Fawcett; R Stone; A comparison of two seasonal rainfall forecasting systems for Australia. Australian Meteorological and Oceanographic Journal 2010, 60, 15–24, 10.22499/2.6001.002.
- F. Mekanik; M.A. Imteaz; S. Gato-Trinidad; Amgad Elmahdi; Multiple regression and Artificial Neural Network for long-term rainfall forecasting using large scale climate modes. Journal of Hydrology 2013, 503, 11-21, 10.1016/j.jhydrol.2013.08.035.
- Mosavi, A.; Rabczuk, T.; Varkonyi-Koczy, A.R. Reviewing the novel machine learning tools for materials design. In Recent Advances in Technology Research and Education; Springer: Cham, Switzerland, 2017; pp. 50–58.
- John Abbot; Jennifer Marohasy; Input selection and optimisation for monthly rainfall forecasting in Queensland, Australia, using artificial neural networks. Atmospheric Research 2014, 138, 166-178, 10.1016/j.atmosres.2013.11.002.
- Neil I. Fox; Christopher K. Wikle; A Bayesian Quantitative Precipitation Nowcast Scheme. Weather and Forecasting 2005, 20, 264-275, 10.1175/waf845.1.
- Bruno Merz; Jim W. Hall; Markus Disse; A. Schumann; Fluvial flood risk management in a changing world. Natural Hazards and Earth System Sciences 2010, 10, 509-527, 10.5194/nhess-10-509-2010.
- Z.X. Xu; J. Y. Li; Short-term inflow forecasting using an artificial neural network model. Hydrological Processes 2002, 16, 2423-2439, 10.1002/hyp.1013.
- E.G. Ortiz-Garcia; S. Salcedo-Sanz; C. Casanova-Mateo; Accurate precipitation prediction with support vector classifiers: A study including novel predictive variables and observational data. Atmospheric Research 2014, 139, 128-136, 10.1016/j.atmosres.2014.01.012.
- Soo Youl Kim; Yoshiharu Matsumi; Shun-Qi Pan; Hajime Mase; A real-time forecast model using artificial neural network for after-runner storm surges on the Tottori coast, Japan. Ocean Engineering 2016, 122, 44-53, 10.1016/j.oceaneng.2016.06.017.
- Mosavi, A.; Edalatifar, M. A.; Edalatifar, M. A Hybrid Neuro-Fuzzy Algorithm for Prediction of Reference Evapotranspiration. In Recent Advances in Technology Research and Education; Springer: Cham, Switzerland, 2018; pp. 235–243.
- Dineva, A.; Várkonyi-Kóczy, A.R.; Tar, J.K. Fuzzy expert system for automatic wavelet shrinkage procedure selection for noise suppression. In Proceedings of the 2014 IEEE 18th International Conference on Intelligent Engineering Systems (INES), Tihany, Hungary, 3–5 July 2014; pp. 163–168.
- Suykens, J.A.; Vandewalle, J; Least squares support vector machine classifiers. Neural Process. Lett. 1999, 9, 395-405.
- Mesgana Seyoum Gizaw; Thian Yew Gan; Regional Flood Frequency Analysis using Support Vector Regression under historical and future climate. Journal of Hydrology 2016, 538, 387-398, 10.1016/j.jhydrol.2016.04.041.
- Pezhman Taherei Ghazvinei; Hossein Hassanpour Darvishi; Amir Mosavi; Khamaruzaman Bin Wan Yusof; Meysam Alizamir; Shahaboddin Shamshirband; Mohammad Ahmadi; Sugarcane growth prediction based on meteorological parameters using extreme learning machine and artificial neural network. Engineering Applications of Computational Fluid Mechanics 2018, 12, 738-749, 10.1080/19942060.2018.1526119.
- K.S. Kasiviswanathan; Jianxun He; K. P. Sudheer; Joo-Hwa Tay; Potential application of wavelet neural network ensemble to forecast streamflow for flood management. Journal of Hydrology 2016, 536, 161-173, 10.1016/j.jhydrol.2016.02.044.
- Masoud Ravansalar; Taher Rajaee; Ozgur Kisi; Wavelet-linear genetic programming: A new approach for modeling monthly streamflow. Journal of Hydrology 2017, 549, 461-475, 10.1016/j.jhydrol.2017.04.018.
- Mosavi, A.; Rabczuk, T. Learning and intelligent optimization for material design innovation. In Learning and Intelligent Optimization; Springer: Cham, Switzerland, 2017; pp. 358–363.
- Dandagala, S.; Reddy, M.S.; Murthy, D.S.; Nagaraj, G. Artificial neural networks applications in groundwater hydrology—A review. Artif. Intell. Syst. Mach. Learn. 2017, 9, 182–187.
- Sujay Raghavendra. N; Paresh Chandra Deka; Support vector machine applications in the field of hydrology: A review. Applied Soft Computing 2014, 19, 372-386, 10.1016/j.asoc.2014.02.002.
- Farnaz Fotovatikhah; Manuel Herrera; Shahaboddin Shamshirband; Mohammad Ahmadi; Sina Faizollahzadeh Ardabili; Jalil Piran; Survey of computational intelligence as basis to big flood management: challenges, research directions and future work. Engineering Applications of Computational Fluid Mechanics 2018, 12, 411-437, 10.1080/19942060.2018.1448896.
- Sina F. Ardabili; Bahman Najafi; Meysam Alizamir; Amir Mosavi; Shahaboddin Shamshirband; Timon Rabczuk; Using SVM-RSM and ELM-RSM Approaches for Optimizing the Production Process of Methyl and Ethyl Esters. Energies 2018, 11, 2889, 10.3390/en11112889.
- Liang Ting Tsai; Chih-Chien Yang; Improving measurement invariance assessments in survey research with missing data by novel artificial neural networks. Expert Systems with Applications 2012, 39, 10456-10464, 10.1016/j.eswa.2012.02.048.
- Sivapalan, M.; Blöschl, G.; Merz, R.; Gutknecht, D. Linking flood frequency to long-term water balance: Incorporating effects of seasonality. Water Resour. Res. 2005, 41.
- Holger R. Maier; Ashu Jain; Graeme C. Dandy; K.P. Sudheer; Methods used for the development of neural networks for the prediction of water resource variables in river systems: Current status and future directions. Environmental Modelling & Software 2010, 25, 891-909, 10.1016/j.envsoft.2010.02.003.
- Lafdani, E.K.; Nia, A.M.; Pahlavanravi, A.; Ahmadi, A.; Jajarmizadeh, M. Research article daily rainfall-runoff prediction and simulation using ANN, ANFIS and conceptual hydrological MIKE11/NAM models. Int. J. Eng. Technol. 2013, 1, 32–50.
- Collier, C. Flash flood forecasting: What are the limits of predictability? Q. J. R. Meteorol. Soc. 2007, 133, 3–23.
- Dong-Jun Seo; J. P. Breidenbach; Real-Time Correction of Spatially Nonuniform Bias in Radar Rainfall Data Using Rain Gauge Measurements. Journal of Hydrometeorology 2002, 3, 93-111, 10.1175/1525-7541(2002)003<0093:rtcosn>2.0.co;2.
- M. Grecu; Witold Krajewski; A large-sample investigation of statistical procedures for radar-based short-term quantitative precipitation forecasting. Journal of Hydrology 2000, 239, 69-84, 10.1016/s0022-1694(00)00360-7.
- Robert A. Maddox; Jian Zhang; Bin Yong; Kenneth Howard; Weather Radar Coverage over the Contiguous United States. Weather and Forecasting 2002, 17, 927-934, 10.1175/1520-0434(2002)017<0927:wrcotc>2.0.co;2.
- Marina Campolo; Paolo Andreussi; Alfredo Soldati; River flood forecasting with a neural network model. Water Resources Research 1999, 35, 1191-1197, 10.1029/1998wr900086.
- Om Prakash; K. P. Sudheer; K. Srinivasan; Improved higher lead time river flow forecasts using sequential neural network with error updating. Journal of Hydrology and Hydromechanics 2014, 62, 60-74, 10.2478/johh-2014-0010.
- C. Shu; Taha B. M. J. Ouarda; Regional flood frequency analysis at ungauged sites using the adaptive neuro-fuzzy inference system. Journal of Hydrology 2008, 349, 31-43, 10.1016/j.jhydrol.2007.10.050.
- Mohammad Ashrafi; Lloyd Hock Chye Chua; Chai Quek; Xiaosheng Qin; A fully-online Neuro-Fuzzy model for flow forecasting in basins with limited data. Journal of Hydrology 2017, 545, 424-435, 10.1016/j.jhydrol.2016.11.057.
- Pao-Shan Yu; Tao-Chang Yang; Szu-Yin Chen; Chen-Min Kuo; Hung-Wei Tseng; Comparison of random forests and support vector machine for real-time radar-derived rainfall forecasting. Journal of Hydrology 2017, 552, 92-104, 10.1016/j.jhydrol.2017.06.020.
- Vahid Nourani; Aida Hosseini Baghanam; Jan Adamowski; Ozgur Kisi; Applications of hybrid wavelet–Artificial Intelligence models in hydrology: A review. Journal of Hydrology 2014, 514, 358-377, 10.1016/j.jhydrol.2014.03.057.
- Mehdi Rezaeianzadeh; Seifollah Amin; Davar Khalili; Vijay P. Singh; Daily Outflow Prediction by Multi Layer Perceptron with Logistic Sigmoid and Tangent Sigmoid Activation Functions. Water Resources Management 2010, 24, 2673-2688, 10.1007/s11269-009-9573-4.
- Lanhai Li; Honggang Xu; Xi Chen; S. P. Simonovic; Streamflow Forecast and Reservoir Operation Performance Assessment Under Climate Change. Water Resources Management 2009, 24, 83-104, 10.1007/s11269-009-9438-x.
- Nasrin Fathollahzadeh Attar; Quoc Bao Pham; Sajad Nowbandegani; Mohammad Rezaie-Balf; Chow Ming Fai; Ali Najah Ahmed; Saeed Pipelzadeh; Duc Dung Tran; Pham Thi Thao Nhi; Nguyen-Khoi Dao; Ahmed El-Shafie; Enhancing the Prediction Accuracy of Data-Driven Models for Monthly Streamflow in Urmia Lake Basin Based upon the Autoregressive Conditionally Heteroskedastic Time-Series Model. Applied Sciences 2020, 10, 571, 10.3390/app10020571.
- Sulaiman, J.; Wahab, S.H. Heavy rainfall forecasting model using artificial neural network for flood prone area. In It Convergence and Security 2017; Springer: Singapore, 2018; pp. 68–76.
- Anil Kumar Karl; Anil Kumar Lohani; Development of Flood Forecasting System Using Statistical and ANN Techniques in the Downstream Catchment of Mahanadi Basin, India. Journal of Water Resource and Protection 2010, 2, 880-887, 10.4236/jwarp.2010.210105.
- Jain, A.; Prasad Indurthy, S. Closure to “comparative analysis of event-based rainfall-runoff modeling techniques—Deterministic, statistical, and artificial neural networks” by ASHU JAIN and SKV prasad indurthy. J. Hydrol. Eng. 2004, 9, 551–553.
- A.K. Lohani; Rakesh Kumar; R.D. Singh; Hydrological time series modeling: A comparison between adaptive neuro-fuzzy, neural network and autoregressive techniques. Journal of Hydrology 2012, 442, 23-35, 10.1016/j.jhydrol.2012.03.031.
- Khandekar Sachin Dadu; Paresh Chandra Deka; Applications of Wavelet Transform Technique in Hydrology—A Brief Review. The Ecology of Transportation: Managing Mobility for the Environment 2016, 73, 241-253, 10.1007/978-3-319-40195-9_19.
- Ozgur Kisi; Streamflow Forecasting Using Different Artificial Neural Network Algorithms. Journal of Hydrologic Engineering 2007, 12, 532-539, 10.1061/(asce)1084-0699(2007)12:5(532).
- A Y Shamseldin; Artificial neural network model for river flow forecasting in a developing country. Journal of Hydroinformatics 2009, 12, 22-35, 10.2166/hydro.2010.027.
- Honey Badrzadeh; Ranjan Sarukkalige; A.W. Jayawardena; Impact of multi-resolution analysis of artificial intelligence models inputs on multi-step ahead river flow forecasting. Journal of Hydrology 2013, 507, 75-85, 10.1016/j.jhydrol.2013.10.017.
- Roberto Baratti; B. Cannas; A. Fanni; M. Pintus; Giovanni M. Sechi; N. Toreno; River flow forecast for reservoir management through neural networks. Neurocomputing 2003, 55, 421-437, 10.1016/s0925-2312(03)00387-4.
- Riccardo Taormina; Mohammad Ahmadi; Rajandrea Sethi; Artificial neural network simulation of hourly groundwater levels in a coastal aquifer system of the Venice lagoon. Engineering Applications of Artificial Intelligence 2012, 25, 1670-1676, 10.1016/j.engappai.2012.02.009.
- Ming-Hsi Hsu; Shu-Horng Lin; Jin-Cheng Fu; Shih-Feng Chung; Albert S. Chen; Longitudinal stage profiles forecasting in rivers for flash floods. Journal of Hydrology 2010, 388, 426-437, 10.1016/j.jhydrol.2010.05.028.
- Dionysia Panagoulia; Artificial neural networks and high and low flows in various climate regimes. Hydrological Sciences Journal 2006, 51, 563-587, 10.1623/hysj.51.4.563.
- A multi-stage methodology for selecting input variables in ANN forecasting of river flows. Global NEST: the international Journal 2017, 19, 49-57, 10.30955/gnj.002067.
- Wen Liu; Mehmet Şahin; Application of the Artificial Neural Network model for prediction of monthly Standardized Precipitation and Evapotranspiration Index using hydrometeorological parameters and climate indices in eastern Australia. Atmospheric Research 2015, 161, 65-81, 10.1016/j.atmosres.2015.03.018.
- Paulin Coulibaly; Yonas Dibike; François Anctil; Downscaling Precipitation and Temperature with Temporal Neural Networks. Journal of Hydrometeorology 2005, 6, 483-496, 10.1175/jhm409.1.
- Justin Schoof; Sara C. Pryor; Downscaling temperature and precipitation: a comparison of regression-based methods and artificial neural networks. International Journal of Climatology 2001, 21, 773-790, 10.1002/joc.655.
- Zulkarnain Hassan; Supiah Shamsudin; Sobri Harun; Marlinda Abdul Malek; Nuramidah Hamidon; Suitability of ANN applied as a hydrological model coupled with statistical downscaling model: a case study in the northern area of Peninsular Malaysia. Environmental Geology 2015, 74, 463-477, 10.1007/s12665-015-4054-y.
- Jia-Shu Zhang; Xian-Ci Xiao; Predicting Chaotic Time Series Using Recurrent Neural Network. Chinese Physics Letters 2000, 17, 88-90, 10.1088/0256-307x/17/2/004.
- Guang-Bin Huang; Qin-Yu Zhu; Chee-Kheong Siew; Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489-501, 10.1016/j.neucom.2005.12.126.
- Aranildo R. Lima; Alex J. Cannon; William W. Hsieh; Forecasting daily streamflow using online sequential extreme learning machines. Journal of Hydrology 2016, 537, 431-443, 10.1016/j.jhydrol.2016.03.017.
- Zaher Mundher Yaseen; Othman Jaafar; Wen Liu; Ozgur Kisi; Jan Adamowski; John Quilty; Ahmed El-Shafie; Stream-flow forecasting using extreme learning machines: A case study in a semi-arid region in Iraq. Journal of Hydrology 2016, 542, 603-614, 10.1016/j.jhydrol.2016.09.035.
- G.B. Sahoo; Chittaranjan Ray; Flow forecasting for a Hawaii stream using rating curves and neural networks. Journal of Hydrology 2006, 317, 63-80, 10.1016/j.jhydrol.2005.05.008.
- Sungwon Kim; Vijay P. Singh; Flood Forecasting Using Neural Computing Techniques and Conceptual Class Segregation. JAWRA Journal of the American Water Resources Association 2013, 49, 1421-1435, 10.1111/jawr.12093.
- David E. Rumelhart; Geoffrey E. Hinton; Ronald J. Williams; Learning representations by back-propagating errors. Nature 1986, 323, 533-536, 10.1038/323533a0.
- A. Sezin Tokar; Peggy A. Johnson; Rainfall-Runoff Modeling Using Artificial Neural Networks. Journal of Hydrologic Engineering 1999, 4, 232-239, 10.1061/(asce)1084-0699(1999)4:3(232).
- A. R. Senthil Kumar; K. P. Sudheer; S. K. Jain; P. K. Agarwal; Rainfall-runoff modelling using artificial neural networks: comparison of network types. Hydrological Processes 2005, 19, 1277-1291, 10.1002/hyp.5581.
- Zadeh, L.A. Soft computing and fuzzy logic. In Fuzzy Sets, Fuzzy Logic, and Fuzzy Systems: Selected Papers by Lotfi a Zadeh; World Scientific: Singapore, 1996; pp. 796–804.
- Bahram Choubin; Shahram Khalighi-Sigaroodi; Arash Malekian; Sajjad Ahmad; Pedram Attarod; Drought forecasting in a semi-arid watershed using climate signals: a neuro-fuzzy modeling approach. Journal of Mountain Science 2014, 11, 1593-1605, 10.1007/s11629-014-3020-6.
- Bahram Choubin; Shahram Khalighi-Sigaroodi; Arash Malekian; Ozgur Kisi; Multiple linear regression, multi-layer perceptron network and adaptive neuro-fuzzy inference system for the prediction of precipitation based on large-scale climate signals. Hydrological Sciences Journal 2016, 61, 1001-1009, 10.1080/02626667.2014.966721.
- Bogardi, I.; Duckstein, L. The fuzzy logic paradigm of risk analysis. In Risk-Based Decisionmaking in Water Resources X; American Society of Civil Engineers: Reston, VA, USA, 2003; pp. 12–22.
- Linda See; Stan Openshaw; A hybrid multi-model approach to river level forecasting. Hydrological Sciences Journal 2000, 45, 523-536, 10.1080/02626660009492354.
- Mukesh K. Tiwari; C. Chatterjee; Development of an accurate and reliable hourly flood forecasting model using wavelet–bootstrap–ANN (WBANN) hybrid approach. Journal of Hydrology 2010, 394, 458-470, 10.1016/j.jhydrol.2010.10.001.
- Celso Augusto Guimarães Santos; Gustavo Barbosa Lima Da Silva; Daily streamflow forecasting using a wavelet transform and artificial neural network hybrid models. Hydrological Sciences Journal 2014, 59, 312-324, 10.1080/02626667.2013.800944.
- Siriporn Supratid; Thannob Aribarg; Seree Supharatid; An Integration of Stationary Wavelet Transform and Nonlinear Autoregressive Neural Network with Exogenous Input for Baseline and Future Forecasting of Reservoir Inflow. Water Resources Management 2017, 31, 4023-4043, 10.1007/s11269-017-1726-2.
- Muhammad Shoaib; A Y Shamseldin; Bruce Melville; Comparative study of different wavelet based neural network models for rainfall–runoff modeling. Journal of Hydrology 2014, 515, 47-58, 10.1016/j.jhydrol.2014.04.055.
- E. Dubossarsky; Jerome H. Friedman; J. T. Ormerod; Matt Wand; Wavelet-based gradient boosting. Statistics and Computing 2014, 26, 93-105, 10.1007/s11222-014-9474-0.
- Turgay Partal; Wavelet regression and wavelet neural network models for forecasting monthly streamflow. Journal of Water and Climate Change 2016, 8, 48-61, 10.2166/wcc.2016.091.
- Maryam Shafaei; Ozgur Kisi; Predicting river daily flow using wavelet-artificial neural networks based on regression analyses in comparison with artificial neural networks and support vector machine models. Neural Computing and Applications 2016, 28, 15-28, 10.1007/s00521-016-2293-9.
- Sanjeet Kumar; Mukesh Kumar Tiwari; Chandranath Chatterjee; Ashok Mishra; Reservoir Inflow Forecasting Using Ensemble Models Based on Neural Networks, Wavelet Analysis and Bootstrap Method. Water Resources Management 2015, 29, 4863-4883, 10.1007/s11269-015-1095-7.
- Youngmin Seo; Sungwon Kim; Ozgur Kisi; Vijay P. Singh; Daily water level forecasting using wavelet decomposition and artificial intelligence techniques. Journal of Hydrology 2015, 520, 224-243, 10.1016/j.jhydrol.2014.11.050.
- Sudhishri, S.; Kumar, A.; Singh, J.K. Comparative evaluation of neural network and regression based models to simulate runoff and sediment yield in an outer Himalayan watershed. J. Agric. Sci. Technol. 2016, 18, 681–694.
- Reshma Khemchandani; Keshav Goyal; Suresh Chandra; TWSVR: Regression via Twin Support Vector Machine. Neural Networks 2016, 74, 14-21, 10.1016/j.neunet.2015.10.007.
- Xiaoqin Shan; Jie Zhou; Feng Xiao; Support Vector Machine Method for Multivariate Density Estimation Based on Copulas. 2011 International Conference on Internet Computing and Information Services 2011, null, 140-143, 10.1109/icicis.2011.41.
- Li, S.; Ma, K.; Jin, Z.; Zhu, Y. A new flood forecasting model based on SVM and boosting learning algorithms. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016; pp. 1343–1348.
- Majid Dehghani; Bahram Saghafian; Farzin Nasiri Saleh; Ashkan Farokhnia; Roohollah Noori; Uncertainty analysis of streamflow drought forecast using artificial neural networks and Monte-Carlo simulation. International Journal of Climatology 2013, 34, 1169-1180, 10.1002/joc.3754.
- Yonas Dibike; Slavco Velickov; Dimitri Solomatine; Michael B. Abbott; Model Induction with Support Vector Machines: Introduction and Applications. Journal of Computing in Civil Engineering 2001, 15, 208-216, 10.1061/(asce)0887-3801(2001)15:3(208).
- Munir Ahmad Nayak; Subimal Ghosh; Prediction of extreme rainfall event using weather pattern recognition and support vector machine classifier. Meteorology and Atmospheric Physics 2013, 114, 583-603, 10.1007/s00704-013-0867-3.
- Francesco Granata; Rudy Gargano; Giovanni De Marinis; Support Vector Regression for Rainfall-Runoff Modeling in Urban Drainage: A Comparison with the EPA’s Storm Water Management Model. Water 2016, 8, 69, 10.3390/w8030069.
- Yicheng Gong; Yongxiang Zhang; Shuangshuang Lan; Huan Wang; A Comparative Study of Artificial Neural Networks, Support Vector Machines and Adaptive Neuro Fuzzy Inference System for Forecasting Groundwater Levels near Lake Okeechobee, Florida. Water Resources Management 2015, 30, 375-391, 10.1007/s11269-015-1167-8.
- Milad Jajarmizadeh; Elham Kakaei Lafdani; Sobri Harun; Azadeh Ahmadi; Application of SVM and SWAT models for monthly streamflow prediction, a case study in South of Iran. KSCE Journal of Civil Engineering 2014, 19, 345-357, 10.1007/s12205-014-0060-y.
- Yukun Bao; Tao Xiong; Zhongyi Hu; Multi-step-ahead time series prediction using multiple-output support vector regression. Neurocomputing 2014, 129, 482-493, 10.1016/j.neucom.2013.09.010.
- Da Wei Han; Ian Cluckie; Shie-Yui Liong; Kok-Kwang Phoon; Vladan Babovic; SUPPORT VECTOR MACHINES IDENTIFICATION FOR RUNOFF MODELLING. Hydroinformatics 2004, null, 1597-1604, 10.1142/9789812702838_0197.
- Mahyat Shafapour Tehrany; Biswajeet Pradhan; Shattri Mansor; Noordin Ahmad; Flood susceptibility assessment using GIS-based support vector machine model with different kernel types. CATENA 2015, 125, 91-101, 10.1016/j.catena.2014.10.017.
- Ozgur Kisi; Kulwinder Singh Parmar; Application of least square support vector machine and multivariate adaptive regression spline models in long term prediction of river water pollution. Journal of Hydrology 2016, 534, 104-112, 10.1016/j.jhydrol.2015.12.014.
- Shie-Yui Liong; Chandrasekaran Sivapragasam; FLOOD STAGE FORECASTING WITH SUPPORT VECTOR MACHINES. JAWRA Journal of the American Water Resources Association 2002, 38, 173-186, 10.1111/j.1752-1688.2002.tb01544.x.
- D. A. Sachindra; F. Huang; Andrew Barton; B. J. C. Perera; Least square support vector and multi-linear regression for statistically downscaling general circulation model outputs to catchment streamflows. International Journal of Climatology 2012, 33, 1087-1106, 10.1002/joc.3493.
- Glenn De'ath; Katharina E. Fabricius; Classification and Regression Trees: A Powerful Yet Simple Technique for Ecological Data Analysis. Ecology 2000, 81, 3178-3192, 10.2307/177409.
- Mahyat Shafapour Tehrany; Biswajeet Pradhan; Mustafa Neamah Jebur; Spatial prediction of flood susceptible areas using rule based decision tree (DT) and a novel ensemble bivariate and multivariate statistical models in GIS. Journal of Hydrology 2013, 504, 69-79, 10.1016/j.jhydrol.2013.09.034.
- Majid Dehghani; Bahram Saghafian; Firoozeh Rivaz; Ahmad Khodadadi; Evaluation of dynamic regression and artificial neural networks models for real-time hydrological drought forecasting. Arabian Journal of Geosciences 2017, 10, , 10.1007/s12517-017-2990-4.
- Bahram Choubin; Gholamreza Zehtabian; Ali Azareh; Elham Rafiei-Sardooi; Farzaneh Sajedi Hosseini; Ozgur Kisi; Precipitation forecasting using classification and regression trees (CART) model: a comparative study of different approaches. Environmental Geology 2018, 77, 314, 10.1007/s12665-018-7498-z.
- Bahram Choubin; Hamid Darabi; Omid Rahmati; Farzaneh Sajedi Hosseini; Bjørn Kløve; River suspended sediment modelling using the CART model: A comparative study of machine learning techniques. Science of The Total Environment 2018, 615, 272-281, 10.1016/j.scitotenv.2017.09.293.
- Mikio Kaihara; Satoshi Kikuchi; Discriminant Analysis of Countries Growing Wakame Seaweeds: A Preliminary Comparison of Visible-Near Infrared Spectra Using Soft Independent Modelling, Randomforests and Classification and Regression Trees. Journal of Near Infrared Spectroscopy 2007, 15, 371-377, 10.1255/jnirs.752.
- Zhaoli Wang; Lai Chengguang; Xiaohong Chen; Bing Yang; Shiwei Zhao; Xiaoyan Bai; Flood hazard risk assessment model based on random forest. Journal of Hydrology 2015, 527, 1130-1141, 10.1016/j.jhydrol.2015.06.008.
- Mahyat Shafapour Tehrany; Biswajeet Pradhan; Mustafa Neamah Jebur; Flood susceptibility mapping using a novel ensemble weights-of-evidence and support vector machine models in GIS. Journal of Hydrology 2014, 512, 332-343, 10.1016/j.jhydrol.2014.03.008.
- Dieu Tien Bui; Tran Anh Tuan; Harald Klempe; Biswajeet Pradhan; Inge Revhaug; Spatial prediction models for shallow landslide hazards: a comparative assessment of the efficacy of support vector machines, artificial neural networks, kernel logistic regression, and logistic model tree. Landslides 2015, 13, 361-378, 10.1007/s10346-015-0557-6.
- Amir Etemad-Shahidi; J. Mahjoobi; Comparison between M5′ model tree and neural networks for prediction of significant wave height in Lake Superior. Ocean Engineering 2009, 36, 1175-1181, 10.1016/j.oceaneng.2009.08.008.
- Dietterich, T.G. Ensemble methods in machine learning. In International Workshop on Multiple Classifier Systems; Springer: Berlin/Heidelberg, Germany, 2000; pp. 1–15.
- Farzaneh Sajedi Hosseini; Arash Malekian; Bahram Choubin; Omid Rahmati; Sabrina Cipullo; Frederic Coulon; Biswajeet Pradhan; A novel machine learning-based approach for the risk assessment of nitrate groundwater contamination. Science of The Total Environment 2018, 644, 954-962, 10.1016/j.scitotenv.2018.07.054.
- Keegan Moore; Mehmet Kurt; Melih Eriten; D. Michael McFarland; Lawrence A. Bergman; A. F. Vakakis; Wavelet-bounded empirical mode decomposition for measured time series analysis. Mechanical Systems and Signal Processing 2018, 99, 14-29, 10.1016/j.ymssp.2017.06.005.
- Wen-Chuan Wang; Mohammad Ahmadi; Dong-Mei Xu; Xiao-Yun Chen; Improving Forecasting Accuracy of Annual Runoff Time Series Using ARIMA Based on EEMD Decomposition. Water Resources Management 2015, 29, 2655-2675, 10.1007/s11269-015-0962-6.
- Mohanad S. Al-Musaylh; Wen Liu; Yan Li; Jan F. Adamowski; Two-phase particle swarm optimized-support vector regression hybrid model integrated with improved empirical mode decomposition with adaptive noise for multiple-horizon electricity demand forecasting. Applied Energy 2018, 217, 422-439, 10.1016/j.apenergy.2018.02.140.
- Qi Ouyang; Wenxi Lu; Xin Xin; Yu Zhang; Weiguo Cheng; Ting Yu; Monthly Rainfall Forecasting Using EEMD-SVR Based on Phase-Space Reconstruction. Water Resources Management 2016, 30, 2311-2325, 10.1007/s11269-016-1288-8.
- Zhang, J.; Hou, G.; Ma, B.; Hua, W. Operating characteristic information extraction of flood discharge structure based on complete ensemble empirical mode decomposition with adaptive noise and permutation entropy. J. Vib. Control 2018.
- Honey Badrzadeh; Ranjan Sarukkalige; A.W. Jayawardena; Hourly runoff forecasting for flood risk management: Application of various computational intelligence models. Journal of Hydrology 2015, 529, 1633-1643, 10.1016/j.jhydrol.2015.07.057.
- Gwangseob Kim; Ana Barros; Quantitative flood forecasting using multisensor data and neural networks. Journal of Hydrology 2001, 246, 45-62, 10.1016/s0022-1694(01)00353-5.
- Bahram Saghafian; Amin Haghnegahdar; Majid Dehghani; Effect of ENSO on annual maximum floods and volume over threshold in the southwestern region of Iran. Hydrological Sciences Journal 2017, 62, 1039-1049, 10.1080/02626667.2017.1296229.
- Nektarios Kourgialas; Zoi Dokou; George P. Karatzas; Statistical analysis and ANN modeling for predicting hydrological extremes under climate change scenarios: The example of a small Mediterranean agro-watershed. Journal of Environmental Management 2015, 154, 86-101, 10.1016/j.jenvman.2015.02.034.
- Rabindra K. Panda; Niranjan Pramanik; Biplab Bala; Simulation of river stage using artificial neural network and MIKE 11 hydrodynamic model. Computers & Geosciences 2010, 36, 735-745, 10.1016/j.cageo.2009.07.012.
- Roohollah Noori; A. R. Karbassi; Ashkan Farokhnia; Majid Dehghani; Predicting the Longitudinal Dispersion Coefficient Using Support Vector Machine and Adaptive Neuro-Fuzzy Inference System Techniques. Environmental Engineering Science 2009, 26, 1503-1510, 10.1089/ees.2008.0360.
- Augusto José Pereira Filho; Cláudia Cristina Dos Santos; Modeling a densely urbanized watershed with an artificial neural network, weather radar and telemetric data. Journal of Hydrology 2006, 317, 31-48, 10.1016/j.jhydrol.2005.05.007.
- Zhang Jingyi; M.J. Hall; Regional flood frequency analysis for the Gan-Ming River basin in China. Journal of Hydrology 2004, 296, 98-117, 10.1016/j.jhydrol.2004.03.018.
- Sajjad Ahmad; Slobodan P. Simonovic; An artificial neural network model for generating hydrograph from hydro-meteorological parameters. Journal of Hydrology 2005, 315, 236-251, 10.1016/j.jhydrol.2005.03.032.
- Qin Ju; Zhongbo Yu; Zhenchun Hao; Gengxin Ou; Jian Zhao; Dedong Liu; Division-based rainfall-runoff simulations with BP neural networks and Xinanjiang model. Neurocomputing 2009, 72, 2873-2883, 10.1016/j.neucom.2008.12.032.
- G.B. Sahoo; Chittaranjan Ray; E.H. De Carlo; Use of neural network to predict flash flood and attendant water qualities of a mountainous stream on Oahu, Hawaii. Journal of Hydrology 2006, 327, 525-538, 10.1016/j.jhydrol.2005.11.059.
- Ghose, D.K. Measuring Discharge Using Back-Propagation Neural Network: A Case Study on Brahmani River Basin; Springer: Singapore, 2018; pp. 591–598.
- Guo-Jian Cheng; Lei Cai; Hua-Xian Pan; Comparison of Extreme Learning Machine with Support Vector Regression for Reservoir Permeability Prediction. 2009 International Conference on Computational Intelligence and Security 2009, 2, 173-176, 10.1109/cis.2009.124.
- Li-Chiu Chang; Pin-An Chen; Ying-Ray Lu; Eric Huang; Kai-Yao Chang; Real-time multi-step-ahead water level forecasting by recurrent neural networks for urban flood control. Journal of Hydrology 2014, 517, 836-846, 10.1016/j.jhydrol.2014.06.013.
- H.-Y. Shen; Li-Chiu Chang; Online multistep-ahead inundation depth forecasts by recurrent NARX networks. Hydrology and Earth System Sciences 2013, 17, 935-945, 10.5194/hess-17-935-2013.
- Michael Bruen; Jianqing Yang; Functional networks in real-time flood forecasting—a novel application. Advances in Water Resources 2005, 28, 899-909, 10.1016/j.advwatres.2005.03.001.
- Yen-Ming Chiang; Li-Chiu Chang; Ben Jong Dao Jou; Pin-Fang Lin; Dynamic ANN for precipitation estimation and forecasting from radar observations. Journal of Hydrology 2007, 334, 250-261, 10.1016/j.jhydrol.2006.10.021.
- B. Bhattacharya; D.P. Solomatine; Neural networks and M5 model trees in modelling water level–discharge relationship. Neurocomputing 2005, 63, 381-396, 10.1016/j.neucom.2004.04.016.
- M. Heiser; C. Scheidl; J. Eisl; B. Spangl; J. Hübl; Process type identification in torrential catchments in the eastern Alps. Geomorphology 2015, 232, 239-247, 10.1016/j.geomorph.2015.01.007.
- Khabat Khosravi; Binh Thai Pham; Kamran Chapi; Ataollah Shirzadi; Himan Shahabi; Inge Revhaug; Indra Prakash; Dieu Tien Bui; A comparative assessment of decision trees algorithms for flash flood susceptibility modeling at Haraz watershed, northern Iran. Science of The Total Environment 2018, 627, 744-755, 10.1016/j.scitotenv.2018.01.266.
- Imen Aichouri; Azzedine Hani; Nabil Bougherira; Larbi Djabri; Hicham Chaffai; Sami Lallahem; River Flow Model Using Artificial Neural Networks. Energy Procedia 2015, 74, 1007-1014, 10.1016/j.egypro.2015.07.832.
- Torabi, M.; Hashemi, S.; Saybani, M.R.; Shamshirband, S.; Mosavi, A. A Hybrid clustering and classification technique for forecasting short-term energy consumption. Environ. Prog. Sustain. Energy 2018, 47.
- Jan Franklin Adamowski; Development of a short-term river flood forecasting method for snowmelt driven floods based on wavelet and cross-wavelet analysis. Journal of Hydrology 2008, 353, 247-266, 10.1016/j.jhydrol.2008.02.013.
- Paul. G. Leahy; Ger Kiely; Gearóid Corcoran; Gerard Kiely; Structural optimisation and input selection of an artificial neural network for river level prediction. Journal of Hydrology 2008, 355, 192-201, 10.1016/j.jhydrol.2008.03.017.
- Chih-Chiang Wei; Soft computing techniques in ensemble precipitation nowcast. Applied Soft Computing 2013, 13, 793-805, 10.1016/j.asoc.2012.10.006.
- R Schiffer, R.A.; Rossow, W.B. The International Satellite Cloud Climatology Project (ISCCP): The first project of the world climate research programme. Bull. Am. Meteorol. Soc. 1983, 64, 779–784.
- Kernel Networks Inc.; Treatment of Functional Abdominal Distension. Case Medical Research 2019, null, , 10.31525/ct1-nct04043208.
- Patricia Jimeno-Sáez; Javier Senent-Aparicio; Julio Pérez-Sánchez; David Pulido-Velazquez; José M. Cecilia; Estimation of Instantaneous Peak Flow Using Machine-Learning Models and Empirical Formula in Peninsular Spain. Water 2017, 9, 347, 10.3390/w9050347.
- Fi-John Chang; Ya-Ting Chang; Adaptive neuro-fuzzy inference system for prediction of water level in reservoir. Advances in Water Resources 2006, 29, 1-10, 10.1016/j.advwatres.2005.04.015.
- Mosavi, A.; Lopez, A.; Varkonyi-Koczy, A.R. Industrial Applications of Big Data: State of the Art Survey. In Recent Advances in Technology Research and Education; Springer: Cham, Switzerland, 2017; pp. 225–232.
- Rezaeianzadeh, M.; Tabari, H.; Yazdi, A.A.; Isik, S.; Kalin, L; Flood flow forecasting using ANN, ANFIS and regression models. Neural Comput. Appl. 2014, 25, 25–37.
- Mahyat Shafapour Tehrany; Biswajeet Pradhan; Mustafa Neamah Jebur; Flood susceptibility analysis and its verification using a novel ensemble support vector machine and frequency ratio method. Stochastic Environmental Research and Risk Assessment 2015, 29, 1149-1165, 10.1007/s00477-015-1021-9.




