1. Introduction

Among the natural disasters, floods are the most destructive, causing massive damage to human life, infrastructure, agriculture, and the socioeconomic system. Governments, therefore, are under pressure to develop reliable and accurate maps of flood risk areas and further plan for sustainable flood risk management focusing on prevention, protection, and preparedness ^[1]. Flood prediction models are of significant importance for hazard assessment and extreme event management. Robust and accurate prediction contribute highly to water recourse management strategies, policy suggestions and analysis, and further evacuation modeling ^[2]. Thus, the importance of advanced systems for short-term and long-term prediction for flood and other hydrological events is strongly emphasized to alleviate damage ^[3]. However, the prediction of flood lead time and occurrence location is fundamentally complex due to the dynamic nature of climate condition. Therefore, today's major flood prediction models are mainly data-specific and involve various simplified assumptions ^[4]. Thus, to mimic the complex mathematical expressions of physical processes and basin behavior, such models benefit from specific techniques e.g., event-driven, empirical black box, lumped and distributed, stochastic, deterministic, continuous, and hybrids ^[5].

Physically based models ^[6] were long used to predict hydrological events, such as storm ^[7][8], rainfall/runoff ^[9][10], shallow water condition ^[11], hydraulic models of flow ^[12][13], and further global circulation phenomena ^[14], including the coupled effects of atmosphere, ocean, and floods ^[15]. Although physical models showed great capabilities for predicting a diverse range of flooding scenarios, they often require various types of hydro-geomorphological monitoring datasets, requiring intensive computation, which prohibits short-term prediction ^[16]. Furthermore, as stated in Reference ^[17], the development of physically based models often requires in-depth knowledge and expertise regarding hydrological parameters, reported to be highly challenging. Moreover, numerous studies suggest that there is a gap in short-term prediction capability of physical models (Costabile and Macchione ^[15]). For instance, on many occasions, such models failed to predict properly ^[18]. Van den Honert and McAneney ^[18] documented the failure in the prediction of floods accrued in Queensland, Australia in 2010. Similarly, numerical prediction models ^[19] were reported in the advancement of deterministic calculations, and were not reliable due to systematic errors ^[20]. Nevertheless, major improvements in physically based models of flood were recently reported through the hybridization of models ^[21], as well as advanced flow simulations ^[22][23].

In addition to numerical and physical models, data-driven models also have a long tradition in flood modeling, which recently gained more popularity. Data-driven methods of prediction assimilate the measured climate indices and hydro-meteorological parameters to provide better insight. Among them, statistical models of autoregressive moving average (ARMA) ^[24], multiple linear regression (MLR) ^[25], and autoregressive integrated moving average (ARIMA) ^[26] are the most common flood frequency analysis (FFA) methods for modeling flood prediction. FFA was among the early statistical methods for predicting floods ^[27]. Regional flood frequency analyses (RFFA) ^[28], more advanced versions, were reported to be more efficient when compared to physical models considering computation cost and generalization. Assuming floods as stochastic processes, they can be predicted using certain probability distributions from historical streamflow data ^[29]. For instance, the climatology average method (CLIM) ^[28], empirical orthogonal function (EOF) ^[30], multiple linear regressions (MLR), quantile regression techniques (QRT) ^[31], and Bayesian forecasting models ^[32] are widely used for predicting major floods. However, they were reported to be unsuitable for short-term prediction, and, in this context, they need major improvement due to the lack of accuracy, complexity of the usage, computation cost, and robustness of the method. Furthermore, for reliable long-term prediction, at least, a decade of data from measurement gauges should be analyzed for a meaningful forecast ^[32]. In the absence of such a dataset, however, FFA can be done using hydrologic models of RFFA, e.g., MISBA ^[33] and Sacramento ^[34], as reliable empirical methods with regional applications, where streamflow measurements are unavailable. In this context, distributed numerical models are used as an attractive solution ^[35]. Nonetheless, they do not provide quantitative flood predictions, and their forecast skill level is "only moderate" and they lack accuracy ^[36].

The drawbacks of the physically based and statistical models mentioned above encourage the usage of advanced data-driven models, e.g., machine learning (ML). A further reason for the popularity of such models is that they can numerically formulate the flood nonlinearity, solely based on historical data without requiring knowledge about the underlying physical processes. Data-driven prediction models using ML are promising tools as they are quicker to develop with minimal inputs. ML is a field of artificial intelligence (AI) used to induce regularities and patterns, providing easier implementation with low computation cost, as well as fast training, validation, testing, and evaluation, with high performance compared to physical models, and relatively less complexity ^[37]. The continuous advancement of ML methods over the last two decades demonstrated their suitability for flood forecasting with an acceptable rate of outperforming conventional approaches ^[38]. A recent investigation by Reference ^[39], which compared performance of a number of physical and ML prediction models, showed a higher accuracy of ML models. Furthermore, the literature includes numerous successful experiments of quantitative precipitation forecasting (QPF) using ML methods for different lead-time predictions ^[40][41]. In comparison to traditional statistical models, ML models were used for prediction with greater accuracy ^[42]. Ortiz-García et al. ^[43] described how ML techniques could efficiently model complex hydrological systems such as floods. Many ML algorithms, e.g., artificial neural networks (ANNs) ^[44], neuro-fuzzy ^[45][46], support vector machine (SVM) ^[47], and support vector regression (SVR) ^[48][49], were reported as effective for both short-term and long-term flood forecast. In addition, it was shown that the performance of ML could be improved through hybridization with other ML methods, soft computing techniques, numerical simulations, and/or physical models. Such applications provided more robust and efficient models that can effectively learn complex flood systems in an adaptive manner. Although the literature includes numerous evaluation performance analyses of individual ML models ^{[49][50][51][52]}, there is no definite conclusion reported with regards to which models function better in certain applications. In fact, the literature includes only a limited number of surveys on specific ML methods in specific hydrology fields ^[53][54][55]. Consequently, there is a research gap for a comprehensive literature review in the general applications of ML in all flood resource variables from the perspective of ML modeling and data-driven prediction systems.

Nonetheless, ML algorithms have important characteristics that need to be carefully taken into consideration. The first is that they are as good as their training, whereby the system learns the target task based on past data. If the data is scarce or does not cover varieties of the task, their learning falls short, and hence, they cannot perform well when they are put into work. Therefore, using robust data enrichment is essential through, e.g., implementing a distribution function of sums of weights ^[56], invariance assessments to retain the group characteristics ^[57], or recovering the missing variables using causally dependent coefficients ^[58].

The second aspect is the capability of each ML algorithm, which may vary across different types of tasks. This can also be called a "generalization problem", which indicates how well the trained system can predict cases it was not trained for, i.e., whether it can predict beyond the range of the training dataset. For example, some algorithms may perform well for short-term predictions, but not for long-term predictions. These characteristics of the algorithms need to be clarified with respect to the type and amount of available training data, and the type of prediction task, e.g., water level and streamflow. In this review, we look into examples of the use of various ML algorithms for various types of tasks. At the abstract level, we decided to divide the target tasks into short-term and long-term prediction. We then reviewed ML applications for flood-related tasks, where we structured ML methods as single methods and hybrid methods. Hybrid methods are those that combine more than one ML method.

Here, we should note that this paper surveys ML models used for predictions of floods on sites where rain gauges or intelligent sensing systems used. Our goal was to survey prediction models with various lead times to floods at a particular site. From this perspective, spatial flood prediction was not involved in this study, as we did not study prediction models used to estimate/identify the location of floods. In fact, we were concerned only with the lead time for an identified site.

2. Method and Outline

This survey identifies the state of the art of ML methods for flood prediction where peer-reviewed articles in top-level subject fields are reviewed. Among the articles identified, through search queries using the search strategy, those including the performance evaluation and comparison of ML methods were given priority to be included in the review to identify the ML methods that perform better in particular applications. Furthermore, to choose an article, four types of quality measure for each article were considered, i.e., source normalized impact per paper (SNIP), CiteScore, SCImago journal rank (SJR), and h-index. The papers were reviewed in terms of flood resource variables, ML methods, prediction type, and the obtained results.

The applications in flood prediction can be classified according to flood resource variables, i.e., water level, river flood, soil moisture, rainfall–discharge, precipitation, river inflow, peak flow, river flow, rainfall–runoff, flash flood, rainfall, streamflow, seasonal stream flow, flood peak discharge, urban flood, plain flood, groundwater level, rainfall stage, flood frequency analysis, flood quantiles, surge level, extreme flow, storm surge, typhoon rainfall, and daily flows ^[59]. Among these key influencing flood resource variables, rainfall and the spatial examination of the hydrologic cycle had the most remarkable role in runoff and flood modeling ^[60]. This is the reason why quantitative rainfall prediction, including avalanches, slush flow, and melting snow, is traditionally used for flood prediction, especially in the prediction of flash floods or short-term flood prediction ^[61]. However, rainfall prediction was shown to be inadequate for accurate flood prediction. For instance, the prediction of streamflow in a long-term flood prediction scenario depends on soil moisture estimates in a catchment, in addition to rainfall ^[62]. Although, high-resolution precipitation forecasting is essential, other flood resource variables were considered in the ^[63]. Thus, the methodology of this literature review aims to include the most effective flood resource variables in the search queries.

A combination of these flood resource variables and ML methods was used to implement the complete list of search queries. Note that the ML methods for flood prediction may vary significantly according to the application, dataset, and prediction type. For instance, ML methods used for short-term water level prediction are significantly different from those used for long-term streamflow prediction. Figure 1 represents the organization of the search queries and further describes the survey search methodology.

The search query included three main search terms. The flood resource variables were considered as term 1 of the search (<Flood resource variable1-n>), which included 25 keywords for search queries mentioned above. Term 2 of search (<ML method1-m>) included the ML algorithms. The collection of the references ^{[16][26][28][37][38][42][44]} provides a complete list of ML methods, from which the 25 most popular algorithms in engineering applications were used as the keywords of this search. Term 3 included the four search terms most often used in describing flood prediction, i.e., "prediction", "estimation", "forecast", or "analysis". The total search resulted in 6596 articles. Among them, 180 original research papers were refined through our quality measure included in the survey.

Figure 1. Flowchart of the search queries.

Section 3 presents the state of the art of ML in flood prediction. A technical description on the ML method and a brief background in flood applications are provided. Section 4 presents the survey of ML methods used for short-term flood prediction. Section 5 presents the survey of ML methods used for long-term flood prediction. Section 6 presents the conclusions.

3. State of the Art of ML Methods in Flood Prediction

For creating the ML prediction model, the historical records of flood events, in addition to real-time cumulative data of a number of rain gauges or other sensing devices for various return periods, are often used. The sources of the dataset are traditionally rainfall and water level, measured either by ground rain gauges, or relatively new remote-sensing technologies such as satellites, multisensor systems, and/or radars ^[62]. Nevertheless, remote sensing is an attractive tool for capturing higher-resolution data in real time. In addition, the high resolution of weather radar observations often provides a more reliable dataset compared to rain gauges ^[63]. Thus, building a prediction model based on a radar rainfall dataset was reported to provide higher accuracy in general ^[64]. Whether using a radar-based dataset or ground gauges to create a prediction model, the historical dataset of hourly, daily, and/or monthly values is divided into individual sets to construct and evaluate the learning models. To do so, the individual sets of data undergo training, validation, verification, and testing. The principle behind the ML modeling workflow and the strategy for flood modeling are described in detail in the literature ^[48][65]. Figure 2 represents the basic flow for building an ML model. The major ML algorithms applied to flood prediction include ANNs ^[66], neuro-fuzzy ^[67], adaptive neuro-fuzzy inference systems (ANFIS) ^[68], support vector machines (SVM) ^[69], wavelet neural networks (WNN) ^[70], and multilayer perceptron (MLP) ^[71]. In the following subsections, a brief description and background of these fundamental ML algorithms are presented.

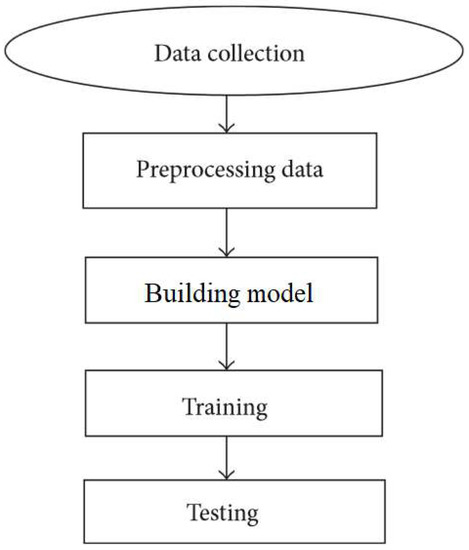
Figure 2. Basic flow for building the machine learning (ML) model.

3.1. Artificial Neural Networks (ANNs)

ANNs are efficient mathematical modeling systems with efficient parallel processing, enabling them to mimic the biological neural network using inter-connected neuron units. Among all ML methods, ANNs are the most popular learning algorithms, known to be versatile and efficient in modeling complex flood processes with a high fault tolerance and accurate approximation ^[39]. In comparison to traditional statistical models, the ANN approach was used for prediction with greater accuracy ^[72]. ANN algorithms are the most popular for modeling flood prediction since their first usage in the 1990s ^[73]. Instead of a catchment's physical characteristics, ANNs derive meaning from historical data. Thus, ANNs are considered as reliable data-driven tools for constructing black-box models of complex and nonlinear relationships of rainfall and flood ^[74], as well as river flow and discharge forecasting ^[75]. Furthermore, a number of surveys (e.g., Reference ^[76]) suggest ANN as one of the most suitable modeling techniques which provide an acceptable generalization ability and speed compared to most conventional models. References ^[77][78] provided reviews on ANN applications in flood. ANNs were already successfully used for numerous flood prediction applications, e.g., streamflow forecasting ^[79], river flow ^[80][81], rainfall–runoff ^[82], precipitation–runoff modeling ^[83], water quality ^[55], evaporation ^[57], river stage prediction ^[84], low-flow estimation ^[85], river flows ^[86], and river time series ^[56]. Despite the advantages of ANNs, there are a number drawbacks associated with using ANNs in flood modeling, e.g., network architecture, data handling, and physical interpretation of the modeled system. A major drawback when using ANNs is the relatively low accuracy, the urge to iterate parameter tuning, and the slow response to gradient-based learning processes ^[87]. Further drawbacks associated with ANNs include precipitation prediction ^[88][89] and peak-value prediction ^[90].

The feed-forward neural network (FFNN) ^[25] is a class of ANN, whereby the network's connections are not in cyclical form. FFNNs are the simplest type of ANN, whereby information moves in a forward direction from input nodes to the hidden layer and later to output nodes. On the other hand, a recurrent neural network (RNN) ^[91] is a class of ANN, whereby the network's connections form a time sequence for dynamic temporal behavior. Furthermore, RNNs benefit from extra memory to analyze input sequences. In ANNs, backpropagation (BP) is a multi-layered NN where weights are calculated using the propagation of the backward error gradient. In BP, there are more phases in the learning cycle, using a function for activation to send signals to the other nodes. Among various ANNs, the backpropagation ANN (BPNN) was identified as the most powerful prediction tool suitable for flood time-series prediction ^[26]. Extreme learning machine (ELM) ^[92] is an easy-to-use form of FFNN, with a single hidden layer. Here, ELM was studied under the scope of ANN methods. ELM for flood prediction recently became of interest for hydrologists and was used to model short-term streamflow with promising results ^[93][94].

3.2. Multilayer Perceptron (MLP)

The vast majority of ANN models for flood prediction are often trained with a BPNN ^[95]. While BPNNs are today widely used in this realm, the MLP—an advanced representation of ANNs— recently gained popularity ^[96]. The MLP ^[97] is a class of FFNN which utilizes the supervised learning of BP for training the network of interconnected nodes of multiple layers. Simplicity, nonlinear activation, and a high number of layers are characteristics of the MLP. Due to these characteristics, the model was widely used in flood prediction and other complex hydrogeological models ^[98]. In an assessment of ANN classes used in flood modeling, MLP models were reported to be more efficient with better generalization ability. Nevertheless, the MLP is generally found to be more difficult to optimize ^[99]. Back-percolation learning algorithms are used to individually calculate the propagation error in hidden network nodes for a more advanced modeling approach.

Here, it is worth mentioning that the MLP, more than any other variation of ANNs (e.g., FFNN, BPNN, and FNN), gained popularity among hydrologists. Furthermore, due to the vast number of case studies using the standard form of MLP, it diverged from regular ANNs. In addition, the authors of articles in the realm of flood prediction using the MLP refer to their models as MLP models. From this perspective, we decided to devote a separate section to the MLP.

3.3. Adaptive Neuro-Fuzzy Inference System (ANFIS)

The fuzzy logic of Zadeh ^[100] is a qualitative modeling scheme with a soft computing technique using natural language. Fuzzy logic is a simplified mathematical model, which works on incorporating expert knowledge into a fuzzy inference system (FIS). An FIS further mimics human learning through an approximation function with less complexity, which provides great potential for nonlinear modeling of extreme hydrological events ^[101][102], particularly floods ^[103]. For instance, Reference ^[104] studied river level forecasting using an FIS, as did Lohani et al. (2011) ^[4] for rainfall–runoff modeling for water level. As an advanced form of fuzzy-rule-based modeling, neuro-fuzzy presents a hybrid of the BPNN and the widely used least-square error method ^[46]. The Takagi–Sugeno (T–S) fuzzy modeling technique ^[4], which is created using neuro-fuzzy clustering, is also widely applied in RFFA ^[28].

Adaptive neuro-FIS, or so-called ANFIS, is a more advanced form of neuro-fuzzy based on the T–S FIS, first coined ^[67][77]. Today, ANFIS is known to be one of the most reliable estimators for complex systems. ANFIS technology, through combining ANN and fuzzy logic, provides higher capability for learning ^[101]. This hybrid ML method corresponds to a set of advanced fuzzy rules suitable for modeling flood nonlinear functions. An ANFIS works by applying neural learning rules for identifying and tuning the parameters and structure of an FIS. Through ANN training, the ANFIS aims at catching the missing fuzzy rules using the dataset ^[67]. Due to fast and easy implementation, accurate learning, and strong generalization abilities, ANFIS became very popular in flood modeling. The study of Lafdani et al. ^[60] further described its capability in modeling short-term rainfall forecasts with high accuracy, using various types of streamflow, rainfall, and precipitation data. Furthermore, the results of Shu and ^[67] showed easier implementation and better generalization capability, using the one-pass subtractive clustering algorithm, which led several rounds of random selection being avoided.

3.4. Wavelet Neural Network (WNN)

Wavelet transform (WT) ^[46] is a mathematical tool which can be used to extract information from various data sources by analyzing local variations in time series ^[50]. In fact, WT has significantly positive effects on modeling performance ^[105]. Wavelet transforms supports the reliable decomposition of an original time series to improve data quality. The accuracy of prediction is improved through discrete WT (DWT), which decomposes the original data into bands, leading to an improvement of flood prediction lead times ^[106]. DWT decomposes the initial data set into individual resolution levels for extracting better-quality data for model building. DWTs, due to their beneficial characteristics, are widely used in flood time-series prediction. In flood modeling, DWTs were widely applied in, e.g., rainfall–runoff ^[51], daily streamflow ^[106], and reservoir inflow ^[107]. Furthermore, hybrid models of DWTs, e.g., wavelet-based neural networks (WNNs) ^[108], which combine WT and FFNNs, and wavelet-based regression models ^[109], which integrate WT and multiple linear regression (MLR), were used in time-series predictions of floods ^[110]. The application of WNN for flood prediction was reviewed in Reference ^[70], where it was concluded that WNNs can highly enhance model accuracy. In fact, most recently, WNNs, due to their potential in enhancing time-series data, gained popularity in flood modeling ^[50], for applications such as daily flow ^[111], rainfall–runoff ^[112], water level ^[113], and flash floods ^[114].

3.5. Support Vector Machine (SVM)

Hearst et al. ^[115] proposed and classified the support vector (SV) as a nonlinear search algorithm using statistical learning theory. Later, the SVM ^[116] was introduced as a class of SV, used to minimize over-fitting and reduce the expected error of learning machines. SVM is greatly popular in flood modeling; it is a supervised learning machine which works based on the statistical learning theory and the structural risk minimization rule. The training algorithm of SVM builds models that assign new non-probabilistic binary linear classifiers, which minimize the empirical classification error and maximize the geometric margin via inverse problem solving. SVM is used to predict a quantity forward in time based on training from past data. Over the past two decades, the SVM was also extended as a regression tool, known as support vector regression (SVR) ^[117].

SVMs are today know as robust and efficient ML algorithms for flood prediction ^[118]. SVM and SVR emerged as alternative ML methods to ANNs, with high popularity among hydrologists for flood prediction. They use the statistical learning theory of structural risk minimization (SRM), which provides a unique architecture for delivering great generalization and superior efficiency. Most importantly, SVMs are both suitable for linear and nonlinear classification, and the efficient mapping of inputs into feature spaces ^[119]. Thus, they were applied in numerous flood prediction cases with promising results, excellent generalization ability, and better performance, compared to ANNs and MLRs, e.g., extreme rainfall ^[120], precipitation ^[43], rainfall–runoff ^[121], reservoir inflow ^[122], streamflow ^[123], flood quantiles ^[48], flood time series ^[124], and soil moisture ^[125]. Unlike ANNs, SVMs are more suitable for nonlinear regression problems, to identify the global optimal solution in flood models ^[126]. Although the high computation cost of using SVMs and their unrealistic outputs might be demanding, due to their heuristic and semi-black-box nature, the least-square support vector machine (LS-SVM) highly improved performance with acceptable computational efficiency ^[127]. The alternative approach of LS-SVM involves solving a set of linear tasks instead of complex quadratic problems ^[128]. Nevertheless, there are still a number of drawbacks that exist, especially in the application of seasonal flow prediction using LS-SVM ^[129].

3.6. Decision Tree (DT)

The ML method of DT is one of the contributors in predictive modeling with a wide application in flood simulation. DT uses a tree of decisions from branches to the target values of leaves. In classification trees (CT), the final variables in a DT contain a discrete set of values where leaves represent class labels and branches represent conjunctions of features labels. When the target variable in a DT has continuous values and an ensemble of trees is involved, it is called a regression tree (RT) ^[130]. Regression and classification trees share some similarities and differences. As DTs are classified as fast algorithms, they became very popular in ensemble forms to model and predict floods ^[131]. The classification and regression tree (CART) ^[132][133], which is a popular type of DT used in ML, was successfully applied to flood modeling; however, its applicability to flood prediction is yet to be fully investigated ^[134]. The random forests (RF) method ^[69][135] is another popular DT method for flood prediction ^[136]. RF includes a number of tree predictors. Each individual tree creates a set of response predictor values associated with a set of independent values. Furthermore, an ensemble of these trees selects the best choice of classes ^[69]. Reference ^[137] introduced RF as an effective alternative to SVM, which often delivers higher performance in flood prediction modeling. Later, Bui et al. ^[138] compared the performances of ANN, SVM, and RF in general applications to floods, whereby RF delivered the best performance. Another major DT is the M5 decision-tree algorithm ^[139]. M5 constructs a DT by splitting the decision space and single attributes, thereby decreasing the variance of the final variable. Further DT algorithms popular in flood prediction include reduced-error pruning trees (REPTs), Naïve Bayes trees (NBTs), chi-squared automatic interaction detectors (CHAIDs), logistic model trees (LMTs), alternating decision trees (ADTs), and exhaustive CHAIDs (E-CHAIDs).

3.7. Ensemble Prediction Systems (EPSs)

A multitude of ML modeling options were introduced for flood modeling with a strong background ^[140]. Thus, there is an emerging strategy to shift from a single model of prediction to an ensemble of models suitable for a specific application, cost, and dataset. ML ensembles consist of a finite set of alternative models, which typically allow more flexibility than the alternatives. Ensemble ML methods have a long tradition in flood prediction. In recent years, ensemble prediction systems (EPSs) ^[141] were proposed as efficient prediction systems to provide an ensemble of N forecasts. In EPS, N is the number of independent realizations of a model probability distribution. EPS models generally use multiple ML algorithms to provide higher performance using an automated assessment and weighting system ^[140]. Such a weighting procedure is carried out to accelerate the performance evaluation process. The advantage of EPS is the timely and automated management and performance evaluation of the ensemble algorithms. Therefore, the performance of EPS, for flood modeling in particular, can be improved. EPSs may use multiple fast-learning or statistical algorithms as classifier ensembles, e.g., ANNs, MLP, DTs, rotation forest (RF) bootstrap, and boosting, allowing higher accuracy and robustness. The subsequent ensemble prediction systems can be used to quantify the probability of floods, based on the prediction rate used in the event ^{[142][143][144]}. Therefore, the quality of ML ensembles can be calculated based on the verification of probability distribution. Ouyang et al ^[145] and Zhang et al. ^[146] presented a review of the applications of ensemble ML methods used for floods. EPSs were demonstrated to have the capability for improving model accuracy in flood modeling ^{[140][141][142][143][144][145][146]}.

To improve the accuracy of import data and to achieve better dataset management, the ensemble mean was proposed as a powerful approach coupled with ML methods ^[140][141]. Empirical mode decomposition (EMD) ^[142], and ensemble EMD (EEMD) ^[143] are widely used for flood prediction ^[144]. Nevertheless, EMD-based forecast models are also subject to a number of drawbacks ^[145]. The literature includes numerous studies on improving the performance of decomposition and prediction models in terms of additivity and generalization ability ^[146].

3.8. Classification of ML Methods and Applications

The most popular ML modeling methods for flood prediction were identified in the previous section, including ANFIS, MLP, WNN, EPS, DT, RF, CART, and ANN. Figure 3 presents the major ML methods used for flood prediction, and the number of corresponding articles in the literature over the last decade. This figure was designed to communicate to the readers which ML methods increased in popularity among hydrologists for flood modeling within the past decade.

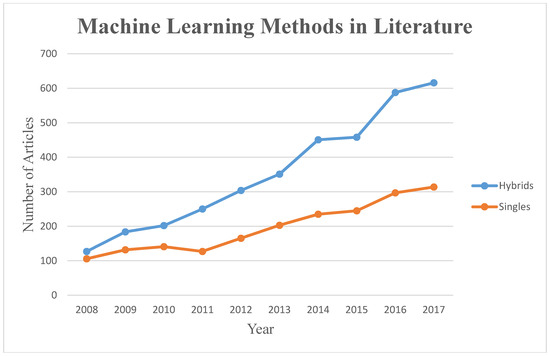
Figure 3. Major ML methods used for flood prediction in the literature. Reference year: 2008 (source: Scopus).

Considering the ML methods for application to floods, it is apparent that ANNs, SVMs, MLPs, DTs, ANFIS, WNNs, and EPSs are the most popular. These ML methods can be categorized as single and hybrid methods. In addition to the fundamental hybrid ML methods, i.e., ANFIS, WNNs, and basic EPSs, several different research strategies for obtaining better prediction evolved ^[137]. The strategies involved developing hybrid ML models using soft computing techniques, statistical methods, and physical models rather than individual ML approaches, whereby the extra components complement each other with respect to their drawbacks and shortcomings. The success of such hybrid approaches motivated the research community to explore more advanced hybrid models. Figure 4 presents the progress of single vs. hybrid ML methods for flood prediction in the literature over the past decade. The figure shows an apparent continuous increase and notable progress in using novel hybrid methods. Through Figure 4, the taxonomy of our research was justified, based on distinguishing hybrid and single ML prediction models.

Figure 4. The progress of single vs. hybrid ML methods for flood prediction in the literature. Reference year: 2008 (source: Scopus).

Furthermore, the types of prediction are often studied with different lead-time predictions due to the flood. Real-time, hourly, daily, weekly, monthly, seasonal, annual, short-term, and long-term are the terms most often used in the literature. Real-time prediction is concerned with anywhere between few minutes and an hour preceding the flood. Hourly predictions can be 1–3 h ahead of the flood forecasting lead time or, in some cases, 18 h or 24 h. Daily predictions can be 1–6 days ahead of the forecast. Monthly forecasts can be, for instance, up to three months. In hydrology, the definitions of short-term and long-term in studying the different phenomena vary. Short-term predictions for floods often refer to hourly, daily, and weekly predictions, and they are used as warning systems. On the other hand, long-term predictions are mostly used for policy analysis purposes. Furthermore, if the prediction leading time to flood is three days longer than the confluence time, the prediction is considered to be long-term ^[37][58]. From this perspective, in this study, we considered a lead time greater than a week as a long-term prediction. It was observed that the characteristics of the ML methods used varied significantly according to the period of prediction. Thus, dividing the survey on the basis of short-term and long-term was essential.

Here, it is also worth emphasizing that, in this paper, the prediction lead-time was classified as "short-term" or "long-term". Although flash floods happen in a short period of time with great destructive power, they can be predicted with either "short-term" or "long-term" lead times to the actual flood. In fact, this paper is concerned with the lead times instead of the duration or type of flood. If the lead-time prediction to a flash flood was short-term, then it was studied as a short-term lead time. However, sometimes flash floods can be predicted with long lead times. In other words, flash floods might be predicted one month ahead. In this case, the prediction was considered as long-term. Regardless of the type of flood, we only focused on the lead time.

In this study, the ML methods were reviewed using two classes—single methods and hybrid methods. Figures 5 and 6 represent the taxonomy of the research.

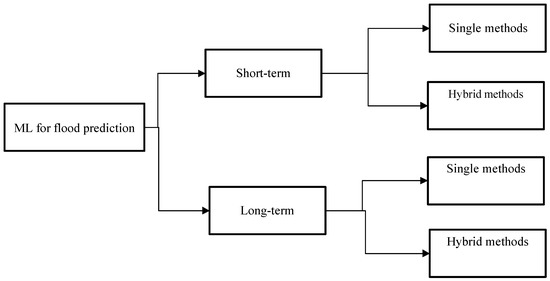
Figure 5. Taxonomy of the survey—ML methods for flood prediction.

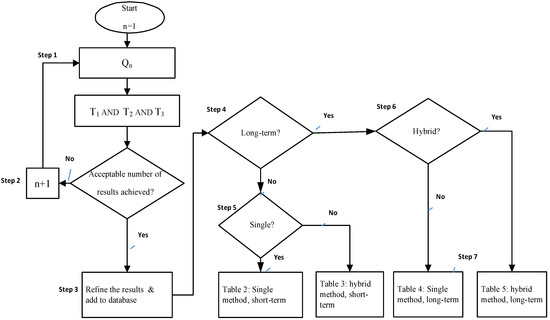
Figure 6. Taxonomy of the survey.

Step 1 involved running the queries one by one; step 2 involved checking the results of the search, and initiating the next search; step 3 involved identifying the comparative studies on ML models of prediction, refining the results and building the database; step 4 involved identifying whether it was a long-term or short-term prediction; steps 5 and 6 involved identifying if it was a single or hybrid method, constructing Table 1, and step 7 involved constructing the other Tables. The four tables provide the list of studies on different prediction techniques, which entail the organized comprehensive surveys of the literature.

4. Short-Term Flood Prediction with ML

Short-term lead-time flood predictions are considered important research challenges, particularly in highly urbanized areas, for timely warnings to residences so to reduce damage ^[146]. In addition, short-term predictions contribute highly to water recourse management. Even with the recent improvements in numerical weather prediction (NWP) models, artificial intelligence (AI) methods, and ML, short-term prediction remains a challenging task ^{[147][148][149][150][151][152]}. This section is divided into two subsections—single and hybrid methods of ML—to individually investigate each group of methods.

4.1. Short-Term Flood Prediction Using Single ML Methods

To gain insight into the performance of ML methods, a comprehensive comparison was required to investigate ML methods. Table 1 presents a summary of the major ML methods, i.e., ANNs, MLP, nonlinear autoregressive network with exogenous inputs (NARX), M5 model trees, DTs, CART, SVR, and RF, followed by a comprehensive performance comparison of single ML methods in short-term flood prediction. A revision and discussion of these methods follow so as to identify the most suitable methods presented in the literature.

Table 1. Short-term predictions using single machine learning (ML) methods.

Kim and Barros ^[148] modified an ANN model to improve flood forecasting short-term lead time through consideration of atmospheric conditions. They used satellite data from the ISCCP-B3 dataset ^[172]. This dataset includes hourly rainfall from 160 rain gauges within the region. The ANN was reported to be considerably more accurate than the statistical models. In another similar work, Reference ^[44] developed an ANN forecast model for hourly lead time. In their study, various datasets were used, consisting of meteorological and hydrodynamic parameters of three typhoons. Testing of the ANN forecast models showed promising results for 5-h lead time. In another attempt, Danso-Amoako ^[1] provided a rapid system for predicting floods with an ANN. They provided a reliable forecasting tool for rapidly assessing floods. An value of 0.70 for the ANN model proved that the tool was suitable for predicting flood variables with a high generalization ability. The results of ^[149] provides similar conclusions. Furthermore, Panda, Pramanik, and Bala ^[151] compared the accuracy of ANN with FFANN, and the results were benchmarked with the physical model of MIKE 11 for short-term water level prediction. This dataset includes the hourly discharge and water level between 2006 and 2009. The data of the year 2006 was used for testing root-mean-square error (RMSE). The results indicated that the FFANN performed faster and relatively more accurately than the ANN model. Here, it is worth mentioning that the overall results indicated that the neural networks were superior compared to the one-dimensional model MIKE 11. Nevertheless, there were great advancements reported in the implementation of two-dimensional MIKE 11 ^[8].

Kourgialas, Dokou, and Karatzas ^[150] created a modeling system for the prediction of extreme flow based on ANNs 3 h, 12 h, and 19 h ahead of the flood. They analyzed five years of hourly data to investigate the ANN effectiveness in modeling extreme flood events. The results indicated it to be highly effective compared to conventional hydrological models. Lohani, Goel, and Bhatia ^[4] improved the real-time forecasting of rainfall–runoff of foods, and the results were compared to the T–S fuzzy model and the subtractive-clustering-based T–S (TSC-T–S) fuzzy model. They, however, concluded that the fuzzy model provided more accurate predictions with longer lead time. The hourly rainfall data from 1989 to 1995 of a gauge site, in addition to the rainfall during a monsoon, was used. Pereira Filho and dos Santos ^[153] compared the AR model with an ANN in simulating forecast stage level and streamflow. The dataset was created from independent flood events, radar-derived rainfall, and streamflow rain gauges available between 1991 and 1995. The AR and ANN were employed to model short-term flood in an urban area utilizing streamflow and weather data. They showed that the ANN performed better in its verification and it was proposed as a better alternative to the AR model.

Ahmad and Simonovic ^[155] used a BPNN for predicting peak flow utilizing causal meteorological parameters. This dataset included daily discharge data for 1958–1997 from gauging stations. BPNN proved to be a fast and accurate approach with the ability of generalization for application to other locations with similar rivers. Furthermore, to improve the simulation of daily streamflow using BPNN, Reference ^[156] used division-based backpropagation to obtain satisfying results. The raw data of local evaporation and rainfall gauges of six years were used for the short-term flood prediction of a streamflow time series. The dataset of one decade from 1988 was used for training and the dataset of five subsequent years was used for testing. The BPNN model provided promising results; however, it lacked efficiency in using raw data for the time-series prediction of streamflow. In addition, Reference ^[157] showed the application of BPNN for assessing flash floods using measured data. This dataset included 5-min-frequency water quality data and 15-min-frequency rainfall data of 20 years from two rain gauge stations. Their experiments introduced ANN models as simple ML methods to apply, while simultaneously requiring expert knowledge by the user. In addition, their ANN prediction model showed great ability to deal with a noisy dataset. Ghose ^[158] predicted the daily runoff using a BPNN prediction model. The data of daily water level of two years from 2013–2015 were used. The accurate BPNN model was reported with an efficiency of 96.4% and an R² of 0.94 for flood prediction.

Pan, Cheng, and Cai ^[159] compared the performances of ELM and SVM for short-term streamflow prediction. Both methods demonstrated a similar level of accuracy. However, ELM was suggested as a faster method for parameter selection and learning loops. Reference ^[154] also conducted a comparison between fuzzy c-means, ANN, and MLP using a common dataset of sites to investigate ML method efficiency and accuracy. The MLP and ANN methods were proposed as the best methods. Chang, Chen, Lu, Huang, and Chang ^[160] and Reference ^[161] modeled multi-step urban flood forecasts using BPNN and a nonlinear autoregressive network with exogenous input (NARX) for hourly forecasts. The results demonstrated that NARX worked better in short-term lead-time prediction compared to BPNN. The NARX network produced an average R² value of 0.7. This study suggested that the NARX model was effective in urban flood prediction. Furthermore, Valipour et al. ^[24] showed how the accuracy of ANN models could be increased through integration with autoregressive (AR) models.

Bruen and Yang ^[162] modeled real-time rainfall–runoff forecasting for different lead times using FFNN, ARMA, and functional networks. Here, functional networks ^[173] were compared with an FFNN model. The models were tested using a storm time-series dataset. The result was that functional networks allowed quicker training in the prediction of rainfall–runoff processes with different lead times. The models were able to predict floods with short lead times. Reference ^[164] estimated water level–discharge using M5 trees and ANN. This dataset was collected from the period of 1990 to 1998, and the inputs were supplied by computing the average mutual information. The ANN and M5 model tree performed similar in terms of accuracy. Reference ^[166] tested four DT models, i.e., alternating decision trees (ADTs), reduced-error pruning trees (REPTs), logistic model trees (LMTs), and NBTs, using a dataset of 200 floods. The ADT model was reported to perform better for flash-flood prediction for a speedy determination of flood-susceptible areas. In other research, Reference ^[165] compared the performance of an NBT and DT prediction model, using geomorphological disposition parameters. Both models and their hybrids were compared in terms of prediction accuracy in a catchment. The advanced DTs were found to be promising for flood assessment in prone areas. They concluded that an independent dataset and benchmarking of other ML methods were required for judgment of the accuracy and efficiency of the method. Reference ^[171] worked on a dataset including more than 100 tropical cyclones (TCs) affecting a watershed for the hourly prediction of precipitation. The performances of MLP, CART, CHAID, exhaustive CHAID, MLR, and CLIM were compared. The evaluation results showed that MLP and DTs provided better prediction. Reference ^[163] applied a dynamic ANN, as well as a Z–R relation approach for constructing a one-hour-ahead prediction model. This dataset included three-dimensional radar data of typhoon events and rain gauges from 1990 to 2004, including various typhoons. The results indicated that the ANN performed better.

Aichouri, Hani, Bougherira, Djabri, Chaffai, and Lallahem ^[167] implemented an MLP model for flood prediction, and compared the results with the traditional MLR model. The rainfall–runoff daily data from 1986 to 2003 were used for model building. The results and comparative study indicated that the MLP approach performed with better yield for river rainfall–runoff. In a similar research, Reference ^[98] modeled and predicted the river rainfall–runoff relationship through training six years of collected daily rainfall data using MLP and MLR (1990 to 1995). Furthermore, the data of 1996 were used for testing to select the best performing network model. The R² values for the ANN and MLR models were 0.888 and 0.917, respectively, showing that the MLP approach gave a much better prediction than MLR. Reference ^[169] proposed a number of data-based flood predictions for daily stream flows models using MLP, WT, MLR, ARIMA, and ANN. This dataset included two time series of streamflow and a meteorological dataset including records from 1970 to 2001. The results showed that MLP, WT, and ANN performed generally better. However, the proposed WT prediction model was evaluated to be not as accurate as ANN and MLP for a one-week lead time. Reference ^[170] designed optimal models of ANN and MLP for the prediction of river level. This study indicated that an optimization tool for the ANN network can highly improve prediction quality. The candidate inputs included river levels and mean sea-level pressure (SLP) for the period of 2001–2002. The MLP was identified as the most accurate model for short-term river flood prediction.

Nayak and Ghosh ^[120] used SVM and ANN to predict hourly rainfall–runoff using weather patterns. A model of SVM classifier for rainfall prediction was used and the results were compared to ANN and another advanced statistical technique. The SVM model appeared to predict extreme floods better than the ANN. Furthermore, the SVM model proved to function better in terms of uncertainty. Gizaw and Gan ^[48] developed SVR and ANN models for creating RFFA to estimate regional flood quantiles and to assess climate change impact. This dataset included daily precipitation data obtained from gauges from 1950 to 2016. RMSE and R² were used for the evaluation of the models. The SVR model estimated regional flood more accurately than the ANN model. SVR was reported to be a suitable choice for predicting future flood under the uncertainty of climate change scenarios ^[118]. In a similar attempt, Reference ^[69] provided effective real-time flood prediction using a rainfall dataset measured by radar. Two models of RF and SVM were developed and their prediction performances were compared. Their performance comparison revealed the effectiveness of SVM in real-time flood forecasting.

Table 2 represents a comparative analysis of single ML models for the prediction of short-term floods, considering the complexity of the algorithm, ease of use, running speed, accuracy, and input dataset. This table was created based on the revisions that were made on the articles of Table 1 and also the accuracy analysis of Figure 3, where the values of R² and RMSE of the single ML methods were considered. The quality of ML model prediction, in terms of speed, complexity, accuracy, and ease of use, was continuously improved through using ensembles of ML methods, hybridization of ML methods, optimization algorithms, and/or soft computing techniques. This trend of improvement is discussed in detail in the discussion.

Table 2. Comparative analysis of single ML models for the prediction of short-term floods.

4.2. Short-Term Flood Prediction Using Hybrid ML Methods

To improve the quality of prediction, in terms of accuracy, generalization, uncertainty, longer lead time, speed, and computation costs, there is an ever increasing trend in building hybrid ML methods. These hybrid methods are numerous, including more popular ones, such as ANFIS and WNN, and further novel algorithms, e.g., SVM–FR, HEC–HMS–ANN, SAS–MP, SOM–R-NARX, wavelet-based NARX, WBANN, WNN–BB, RNN–SVR, RSVRCPSO, MLR–ANN, FFRM–ANN, and EPSs. Table 3 presents these methods; a revision of the methods and applications follows along with a discussion on the ML methods.

Table 3. Short-term flood prediction using hybrid ML methods.

This entry is adapted from the peer-reviewed paper 10.3390/w10111536