1000/1000
Hot
Most Recent

The strata model inside the earth is close to physical reality. The strata layers can be macro-anisotropic but transversely isotropic, where some are vertically symmetric and the others are not. The macroscopic anisotropy is significant for seismic waves with long wave-length regarding propagation, reflection, refraction, and polarization. This topic review provides the most recent theoretical development related to geophysical applications.
The acoustic waves at the interface between two different types of anisotropic media play an important role in acoustic applications, including geophysical applications [1][2], seismic research [3][4], petroleum logging [5][6][7][8][9], energy conversion device [5][10], and medical imaging device [11].
A good model needs to be as simple as possible while remaining close to physical reality, such as the strata model inside the earth. The strata layers can be macro-anisotropic but transversely isotropic, where some are vertically symmetric and the others not [12]. The macroscopic anisotropy and related properties have been modeled based on the so-called elastic tensor, which is usually reserved for the hexagonal crystals [1][2]. Obviously, macroscopic anisotropy is significant for seismic waves with long wave-length regarding propagation, reflection, refraction, and polarization.
The refraction and reflection coefficients and their corresponding phase factors are the typical physical qualities that deserve special attention. Discussions have been focused mostly on and limited to the models of the transversely isotropic rock layers [13][14][15][16][17][18]. Due to mathematical complexity, there have been temptations and interests in approximate expressions [19][20][21][22] However, the analytic solutions of the amplitudes of the reflected and refracted waves are desirable, yet difficult [23].
For angles of reflection and refraction, at the interface between similar types of strata, a fourth-order polynomial has been established for transversely isotropic media with a vertical axis of symmetry (VTI) [24][25]. At the interface between unlike strata, an eighth-order polynomial has been established for transversely isotropic media with a tilting axis of symmetry (TTI).
While an interface between likewise-media has a relatively simple geometric structure [24][25][26][27][28][29][30][31][32][33][34], the interface between unlike-media can be much more complicated [35].
Sedimentary rocks are typically anisotropic media but treated as transversely isotropic. Mostly, they are polar anisotropic. The VTI and TTI media, as medium models, are the most common structures of the strata, as shown in Figure 1. At the interface between VTI and TTI media, the reflection and refraction coefficients are affected by many factors, including anisotropy, tilting-angle of rock-layer, and incident-angle.
Figure 2 is a schematic presentation of the interface between VTI and TTI media, showing the symmetric axes of the media and the geometric relationship between the VTI and TTI media with a TTI tilt-angle, φ.

Figure 1. A schematic representation of the anisotropic rock media: (a) transversely isotropic media with a vertical axis of symmetry (VTI), (b) transversely isotropic media with a tilting axis of symmetry (TTI) [35].
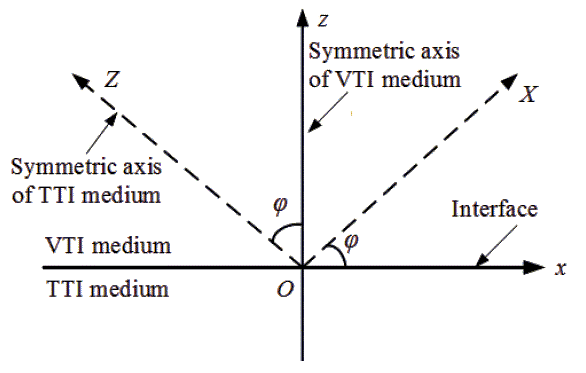
Figure 2. Schematic representation of VTI-TTI media interface, where Z-axis is the symmetric-axis of TTI medium; z-axis is the symmetric-axis of VTI medium, normal to the interface [35].
An incident P-wave from the VTI medium striking on the interface would induce several new waves at the interface, e.g., reflected P-wave, reflected SV-wave, refracted P-wave, and refracted SV-wave, as shown in Figure 3.
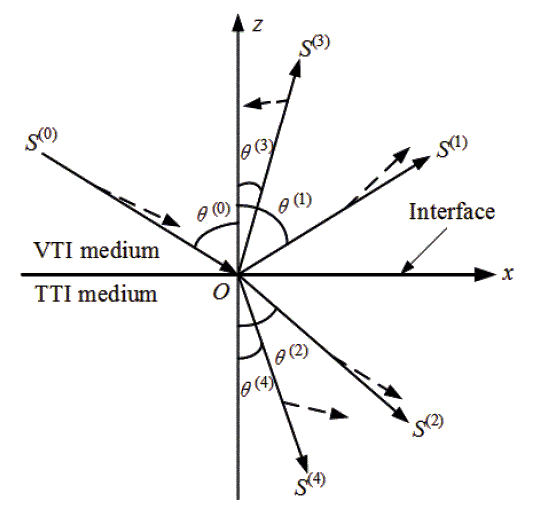
Figure 3. At the interface between VTI and TTI media, a P-wave from VTI medium leads to reflection and refraction, which produces the reflected P-wave, reflected SV-wave, refracted P-wave, and refracted SV-wave, corresponding to the index (1,2,3,4) [35].
The mechanical and physical properties of a general anisotropic medium can be described by an elastic stiffness tensor that may have up to 21 independent elements. The elastic stiffness tensors of the VTI and TTI media have only 5 independent elements [36][37].
Now, consider an incident P-wave from VTI to TTI medium with an incident angle (θ). For the TTI medium, Bond transformation can be used to convert its tilt-angle structure to the same tensor form of the VTI structure [24][25][26][27][28][29][30][31][32][33][34]; Kelvin-Christoffel equation can be solved for the reflected and refracted coefficients; Snell’s law can be applied to determine the angles of reflection and refraction and to guarantee energy conservation.
Inside the incident VTI medium, Snell’s law yields a fourth-order polynomial for the angles of reflection of the reflected P-wave and SV-wave [24][25],
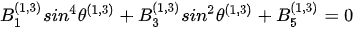 . (1)
. (1)
Inside the refraction TTI medium, an eighth-order polynomial of the angles of refraction is obtained for the refracted P-wave and SV-wave [35],
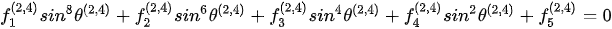 . . (2)
. . (2)
In equations (1)-(2), θ is an incident angle; the coefficients (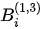 and
and 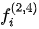 ) are functions of the incident angle, the anisotropy, and the mechanical parameters of the media.
) are functions of the incident angle, the anisotropy, and the mechanical parameters of the media.
Consider the interface between VTI and TTI media, where the TTI medium has a tilting-angle, φ. The typical mechanical and anisotropy parameters for the VTI and TTI media have been reported in the literature [13][14][25][35][38][39]. Typically, the tilting level of the TTI medium shows a significant influence on the critical incident angle, the reflection and refraction coefficients, the magnitude of power density flux, and the state of polarization.
The critical incidence angle (θc), corresponding to the refracted P-wave, has been affected significantly by the tilting level of the TTI medium and its anisotropy, as shown in Table 1. The tilting-angle and anisotropy of the TTI medium also influence the coefficients of the reflection and refraction. The calculated refraction coefficients and corresponding phase angles are shown in Figure 4.
Table 1: The critical incident angle versus the tilting-angle of TTI medium at the interface between VTI and TTI media.
|
TTI tilting-angle, φ |
0° |
45° |
60° |
|
Critical incident-angle, θc |
41.3° |
51.1° |
55.3° |
It should be noted that the reflection and refraction coefficients are not smooth continuous at the angle of critical incidence.
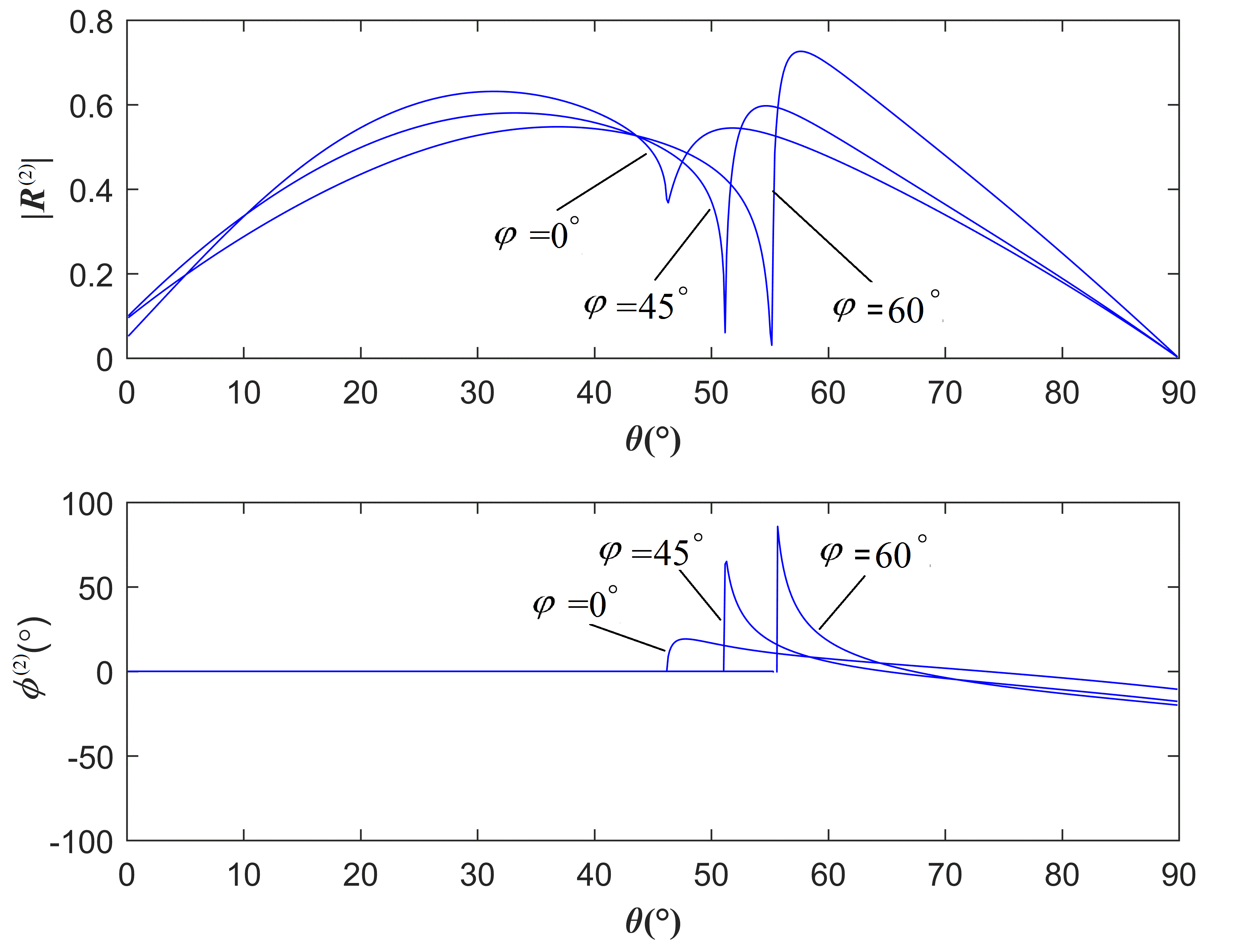
Figure 4. The amplitude and corresponding phase angle of the refracted wave, at the interface between VTI and TTI media, versus incident angle (θ) for three selected values of TTI tilting-angle (φ) [35].
The anisotropy influences the magnitude of power density flux but not the sum of the real parts of power density fluxes of the induced waves in the z-direction. The influence of the tilting-angle is even more significantly on the reflection and refraction coefficients, much more than anisotropy does. The real-parts of the energy density fluxes as a function of incident angle, for the induced waves in the z-direction, are calculated for several parameters and are presented in Figure 5.
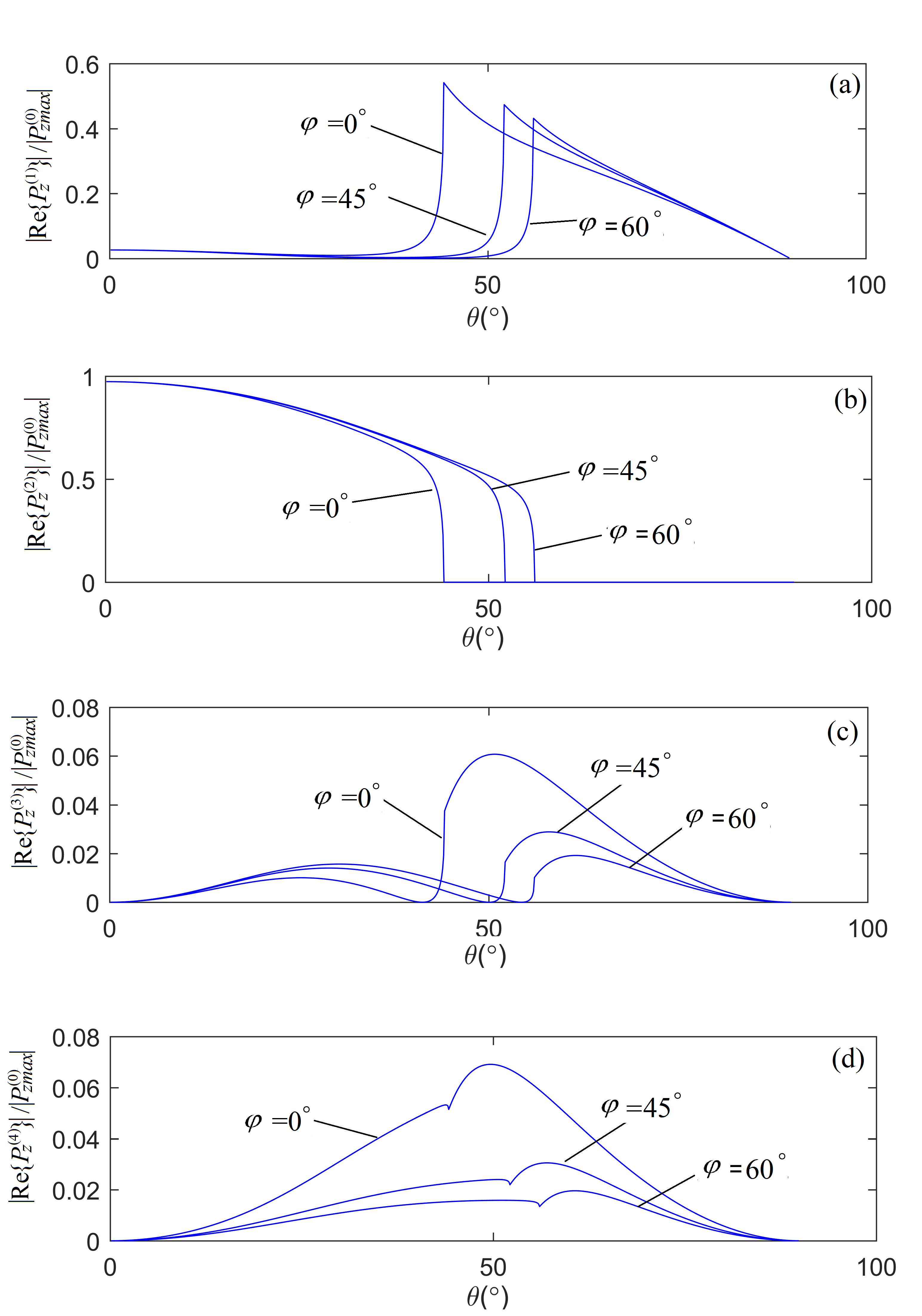
Figure 5. The energy density fluxes of the reflected and refracted waves perpendicular to the interface between VTI and TTI media versus incident angle (θ), for selected tilting-angles (φ) of the TTI media. The blue, red, and black curves are for the cases of TTI tilting-angle φ = 0°, 45°, and 60° [35].
The polarization state of the refracted wave is also influenced by the tilting-angle and anisotropy of the refraction medium [29][31][40].
Prior to the critical incident angle, the polarization coefficients of the waves are all mathematically real numbers, including the incident P-wave, reflected P-wave, reflected SV-waves, refracted P-wave, and refracted SV-wave.
In the post-critical angle region, except for the refracted P-wave, the polarization coefficients are complex numbers for all waves. The polarization coefficients of the refracted P-wave have two possible solutions. Each solution has two independent components (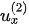 and
and 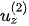 ), where one component is purely real; the other is purely imaginary. If the x-component is purely real, the z-component must be purely imaginary; vice versa. The choice of the solution determines the direction of polarization.
), where one component is purely real; the other is purely imaginary. If the x-component is purely real, the z-component must be purely imaginary; vice versa. The choice of the solution determines the direction of polarization.
Based on our current knowledge from the studies of the VTI-VTI anisotropic media interface, the VTI-TTI interface can be explained, through Bond transformation, by borrowing the techniques used in the VTI-VTI interface. Additional work will lead to improved understanding of the interface between different types of anisotropic media, such as the interface between TVI and TTI anisotropic media. In practical applications for energy conversion, on the transient response of the acoustic-electric transducers, a similar issue may appear for acoustic scattering from spheres and cylinders [41][42][43].
The next steps may include the determinations of anomalous refraction if it ever exists, the effect of the competition between anisotropy and tilting-angle of the media, and the effect of anisotropy and the tilting-angle on polarization conversion. With respect to reflection and refraction, it is extremely desirable to achieve a better understanding of the relative importance of the anisotropy and TTI angle tilting, i.e., the competition between the anisotropy and angle-tilting of the media.