1000/1000
Hot
Most Recent

Nuclear symmetry energy is a measure of the energy cost to make nuclear systems more neutron rich. It depends on the density of the system. Information about the density dependence of nuclear symmetry energy has broad ramifications on the mechanisms of supernova explosions, properties of neutron stars and gravitational waves from their mergers. It is also important for understanding properties of nuclei as well as the dynamics and products of their collisions in laboratory experiments.
The Equation of State (EOS) of uniform neutron-rich nucleonic matter of isospin asymmetry δ = (ρn− ρp)/ρ and density ρ can be expressed in terms of the energy per nucleon E(ρ, δ) within the parabolic approximation as [1][2][3][4].
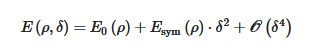
where Esym(ρ) ≈ E(ρ, 1) − E(ρ, 0) is the symmetry energy of asymmetric nuclear matter (ANM). It is approximately the energy cost of converting symmetric nuclear matter (SNM, with equal numbers of protons and neutrons) into pure neutron matter (PNM). Many interesting questions including the dynamics of supernova explosions, heavy-ion collisions, structures of neutron stars and rare isotopes, frequencies and strain amplitudes of gravitational waves from both isolated pulsars and collisions involving neutron stars all depend critically on the EOS of neutron-rich nucleonic matter. Thanks to the great efforts of scientists in both nuclear physics and astrophysics over the last four decades, much knowledge about the EOS of SNM, i.e, the E(ρ, 0) term in Eq. (1), has been obtained. In more recent years, significant efforts have been devoted to exploring the poorly known Esym(ρ) using both terrestrial laboratory experiments and astrophysical observations. Theoretically, essentially all available nuclear forces have been used to calculate the Esym(ρ) within various microscopic many-body theories and/or phenomenological models. However, model predictions still vary largely at both sub-saturation and supra-saturation densities although they agree often by construction at the saturation density ρ0. Therefore, accurate experimental constraints are imperative for making further progresses in our understanding of the density dependence of nuclear symmetry energy.
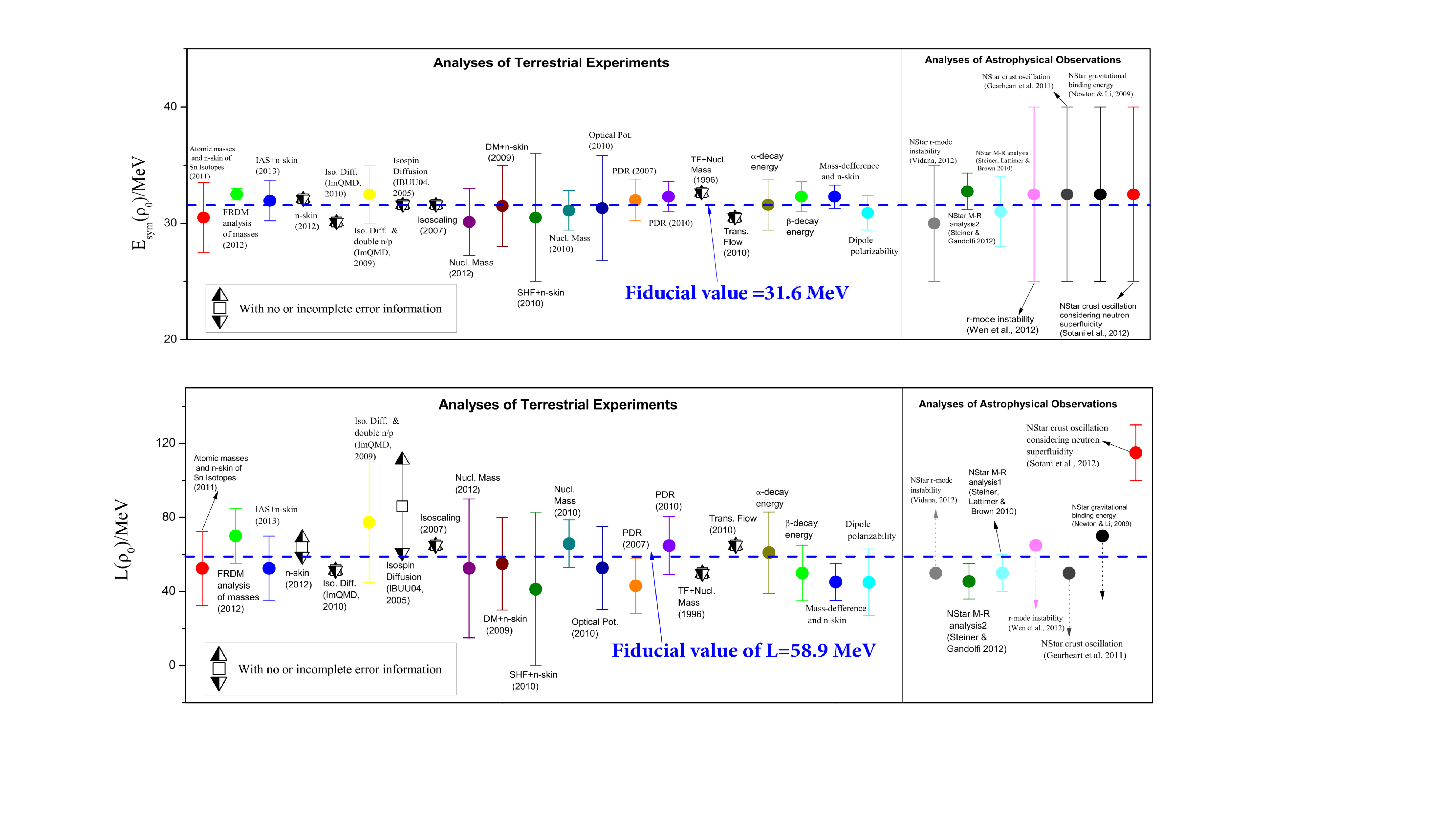
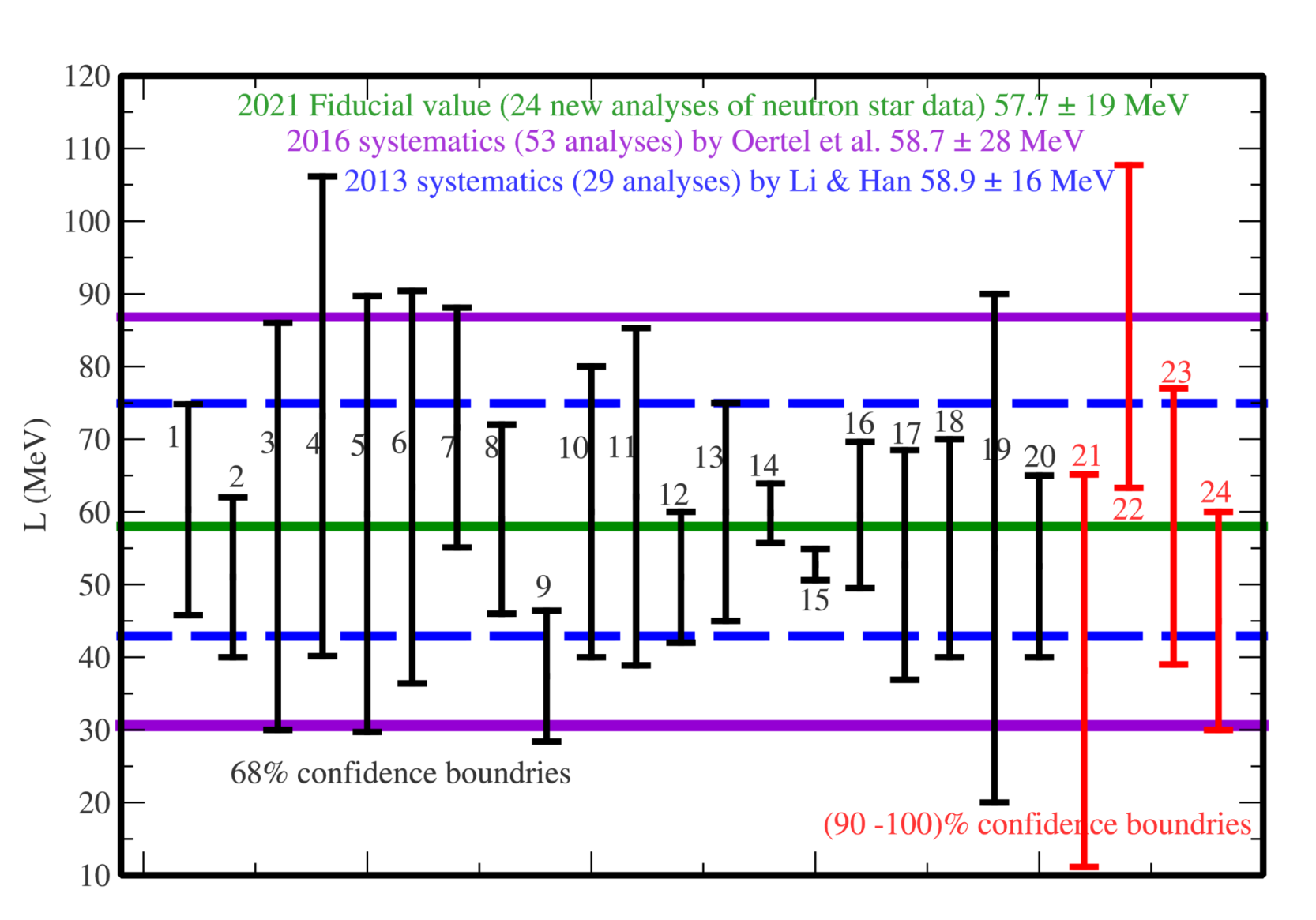
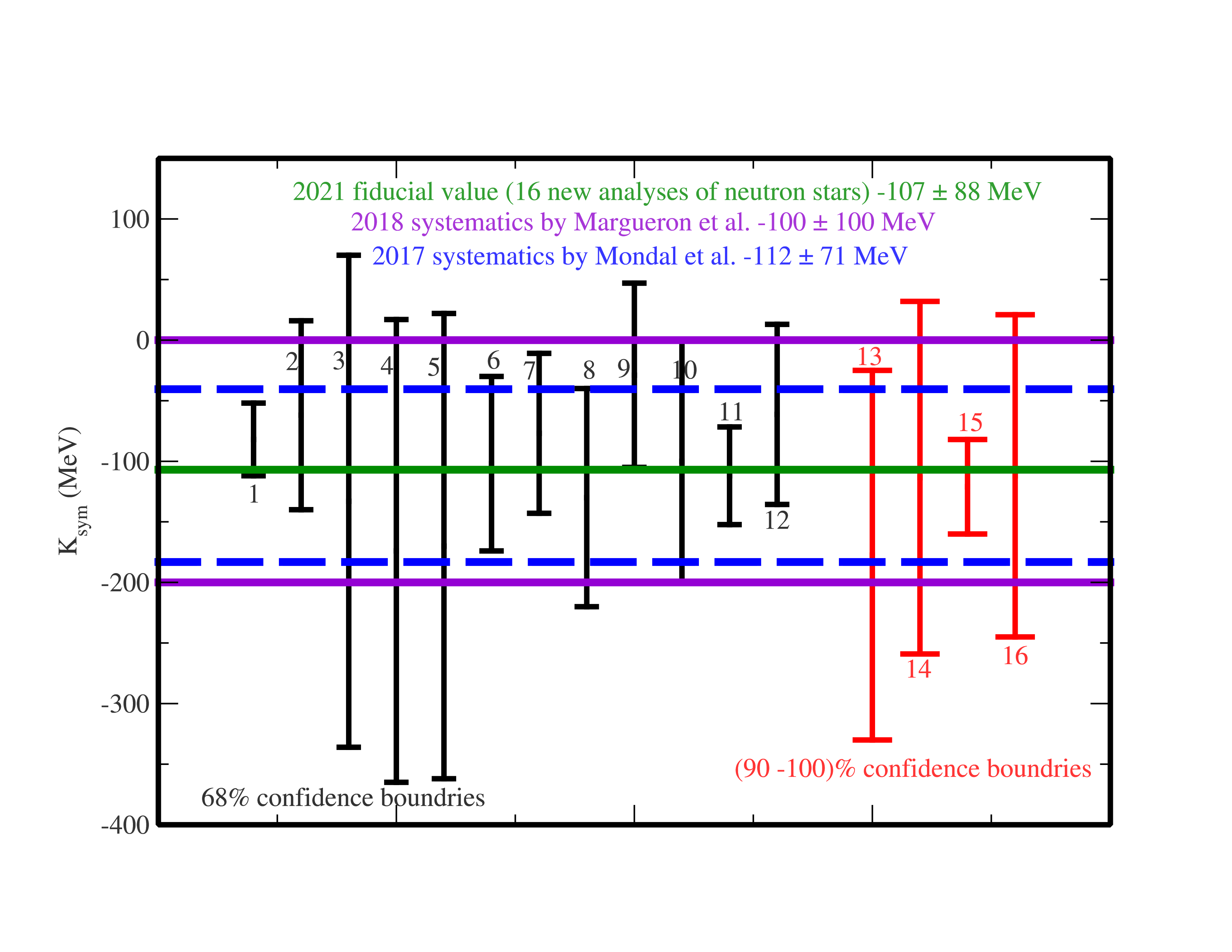
Significant progresses have been made in constraining the Esym(ρ) around and below the saturation density ρ0 over the last two decades. Comprehensive reviews on the recent progress and remaining challenges in constraining the Esym(ρ) can be found in the reviews in Refs. [4][5][6][7][8][9][10][11][12][13][14][15]. The density dependence of nuclear symmetry energy around ρ0 can be characterized by its magnitude Esym(ρ0), slope L and curvature Ksym. Efforts by many people in both nuclear physics and astrophysics especially since the discovery of the first neutron star merger event GW170817 have significantly enriched our knowledge about the symmetry energy and provided tighter constraints on its characteristics as illustrated in the following three figures. The first is from a survey of 29 analyses of various observables in terrestrial nuclear laboratory experiments and astrophysical observations done by 2013 (taken from B.A. Li and X. Han, Phys. Lett. B727, 276 (2013)). Results from 24 new analyses of neutron star observables since the discovery of GW170817 are compared with the 2013 survey in the second figure. While the third figure shows the values of curvature of symmetry energy extracted from the earlier analyses and the new studies of neutron star observables as indicated in the figure.
 While the symmetry energy at supra-saturation densities remains rather uncertain, some interesting information about its magnitude at twice the saturation density of nuclear matter has been obtained from analyses of neutron star observables since GW170817 as shown in the following figure.
While the symmetry energy at supra-saturation densities remains rather uncertain, some interesting information about its magnitude at twice the saturation density of nuclear matter has been obtained from analyses of neutron star observables since GW170817 as shown in the following figure.
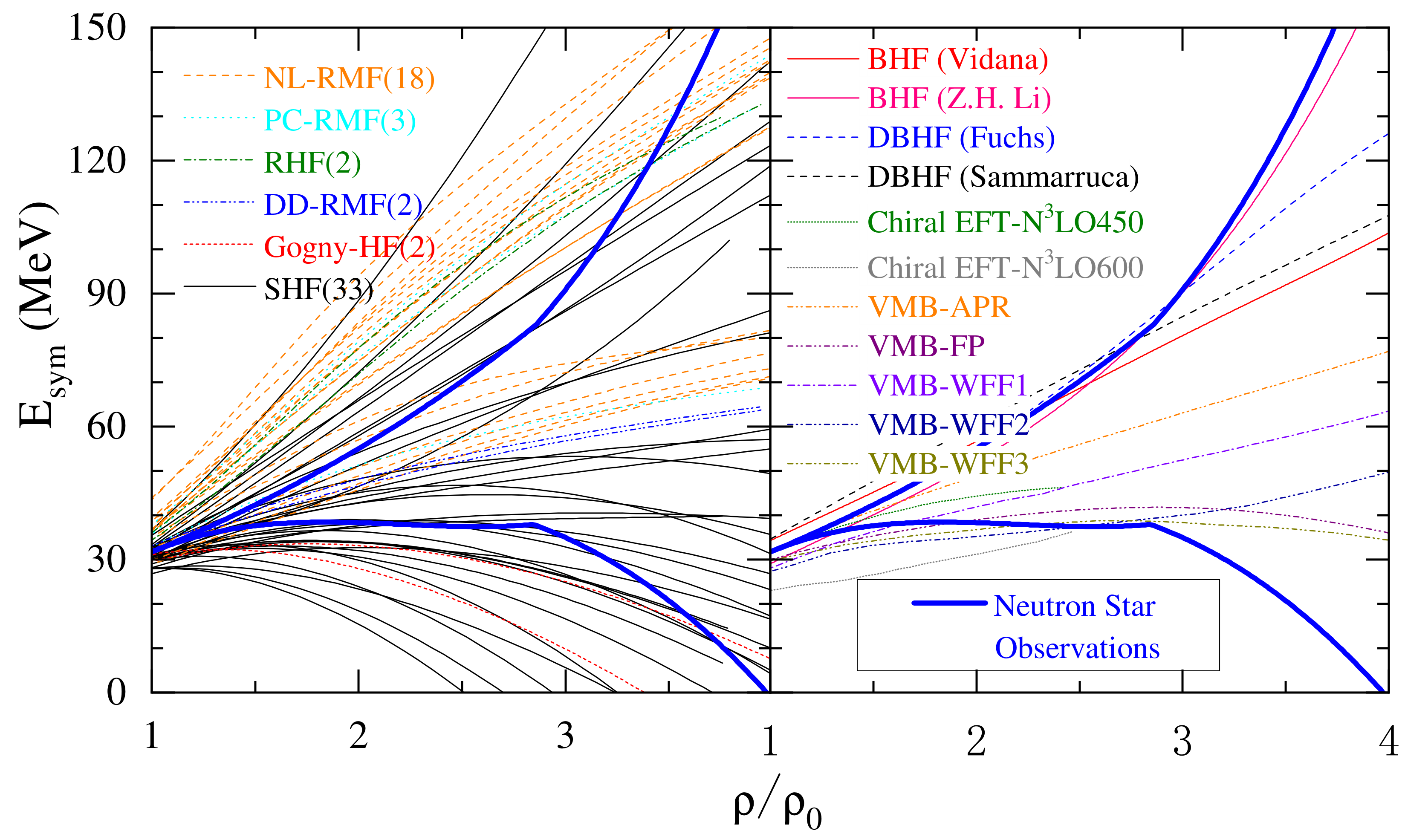
 Shown in the following is a comparison of the upper and lower limits of symmetry energy (blue curves) from analyzing neutron star properties with predictions of phenomenological (left window) and microscopic (right window) nuclear many-body theories. Detailed discussions of these predictions and references can be found in Universe 7 (6), 82 (2021).
Shown in the following is a comparison of the upper and lower limits of symmetry energy (blue curves) from analyzing neutron star properties with predictions of phenomenological (left window) and microscopic (right window) nuclear many-body theories. Detailed discussions of these predictions and references can be found in Universe 7 (6), 82 (2021).
Combining results from ongoing and planned new laboratory experiments with high energy radioactive beams and astrophysical observations using advanced x-ray observatories and next generation gravitational wave detectors has the great promise of determining more precisely the symmetry energy of dense neutron-rich matter in the near future.