Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Di Zhang
 + 2977 word(s) 2977 2021-07-09 08:54:53 |
2 update layout and references
Amina Yu
 + 13 word(s) 2990 2021-07-16 11:01:42 |

Video Upload Options

Do you have a full video?
Send video materials Upload full video

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Zhang, D. Tilting Mapping Function. Encyclopedia. Available online: https://encyclopedia.pub/entry/12108 (accessed on 20 April 2024).
Zhang D. Tilting Mapping Function. Encyclopedia. Available at: https://encyclopedia.pub/entry/12108. Accessed April 20, 2024.
Zhang, Di. "Tilting Mapping Function" Encyclopedia, https://encyclopedia.pub/entry/12108 (accessed April 20, 2024).
Zhang, D. (2021, July 15). Tilting Mapping Function. In Encyclopedia. https://encyclopedia.pub/entry/12108
Zhang, Di. "Tilting Mapping Function." Encyclopedia. Web. 15 July, 2021.
Tilting Mapping Function
Edit
This entry is adapted from the peer-reviewed paper 10.3390/rs13132568

Tilting Mapping Function (TMF) is a tropospheric mapping function to scale the slant tropospheric delays from various elevation and azimuth angles to the zenith direction. Based on the theory of tilting troposphere, TMF can represent the neutral atmosphere's asymmetry more accurately than traditional continued fraction mapping functions.

tropospheric delay ray-trace mapping function tilting troposphere gradient

1. Introduction

Tropospheric delay refers to the effect caused by the propagation of the radio signals among the neutral atmosphere, which can be divided into a hydrostatic part and a wet part [1]. Many regional or global tropospheric delay models have been built to reduce the tropospheric delay error, which can be divided into two categories, depending on whether meteorological factors are needed or not [2]. Models of the first category use pressure, temperature, and humidity as their input parameters, such as Hopfield [3], Saastamoinen [4], Davis [5], Baby [6], Ifadis [7], Askne, Nordius [8], and MSAAS [9]. If in-situ meteorological observations are not available, the standard atmosphere [10][11][12] or empirical meteorological models [13][14][15] may also be used in many GNSS data processing applications. The second category doesn’t rely on meteorological measurements, such as UNB [16], MOPS [17], TropGrid [18], ITG [19], IGGTrop [20], and SHAtropE [21].
However, due to the irregular spatial and temporal distribution of water vapor, it is challenging to precisely model the wet part of the tropospheric delay. Thus it has been a commonly used strategy for Global Navigation Satellites Systems (GNSS) data processing to estimate the tropospheric zenith delay [22][23][24], especially for high precision applications [25][26]. The estimated Zenith Wet Delay (ZWD) can be converted into Precipitable Water Vapor (PWV) [27][28][29], and therefore GNSS meteorology has gradually become a fundamental and effective method for sounding the atmosphere under any weather condition. Barriot, et al. [30] proposed an approach based on perturbation theory, with the ability to separate eddy-scale variations of the wet refractivity.
The mapping function has been used to scale the slant delays from various elevation angles to the zenith direction. Consequently, the mapping function’s accuracy has significant and direct impacts on the determination of the ZWD and station coordinate. Since Marini first proposed the continued fraction form [31], almost all modern mapping functions, including Ifadis [7], MTT [32], NMF [33], IMF [34], UNBabc [35], VMF [36], GMF [37], VMF1 [38], GPT2 [39], and VMF3/GPT3 [40], have taken it as their model expression. Each mapping function has two subtypes: the hydrostatic part and the wet part. The main difference among various mapping functions is the specific value of each coefficient.
However, the Marini concept mapping functions were built on the assumption of the neutral atmosphere’s spherical symmetry [41][42][43], which can be clearly seen from the expression being independent on azimuth (will be discussed in Section 2). This assumption holds only approximately even for the troposphere’s normal state, mainly due to the atmospheric bulge, high variation of tropospheric meteorological parameters such as water vapor and temperature. Therefore, such mapping functions would degrade the estimated ZWD and station height in the GNSS data processing. The tropospheric delay’s horizontal gradients, including a North-South and an East-West component, have been used to model the tropospheric delay’s anisotropy [32][44][45][46]. The inclusion of gradient models can significantly improve the accuracy of slant delays [43], station positions [44][47][48][49][50], zenith delays [51][52], and PWV [27][53]. Nevertheless, only total gradients [54][55][56] can be estimated in the GNSS data processing, since the hydrostatic and wet gradient mapping functions are very similar. Spherical harmonics were used by Zhang [57] (using ray-traced delays) and Zhang, et al. [58] (using GPS-derived delays) to replace the mapping function and gradients. However, many more unknown parameters have to be fitted for those approaches.
To overcome the shortcomings due to the assumption that atmospheric refractivity is spherically symmetric, we tested a new mapping function—TMF—where a concept of tilting the tropospheric zenith by an angle introduced by Gardner [59], Herring [32], Chen, et al. [44], Meindl, et al. [49] is utilized in this study. The TMF takes not only the elevation but also the azimuth as its input parameter. Ray-tracing [60] through Numerical Weather Model (NWM) is one of the most accurate approaches to obtaining tropospheric delays. Hence, ERA5 data [61] of the highest spatio-temporal resolution provided by the European Centre for Medium-range Weather Forecast (ECMWF) was adopted for computing ray-traced delays, using the software WHURT programmed in FORTRAN and developed by Zhang [2]. In the second part, we discuss some critical algorithms for ray-tracing. A detailed definition of the TMF is given. In the third part, we firstly investigate the asymmetry of the slant tropospheric delays. Then the coefficients of TMF are fitted by the Levenberg–Marquardt nonlinear least-squares method, using ray-traced tropospheric delays. Four fitting schemes were compared, with a different spatial resolution of NWM and different sampling on elevations and azimuths. The performance of TMF against mapping functions based on the VMF3 concept, without or with an estimation of gradient parameters, is presented in the results and discussion section. The summaries and conclusions are given in the last part.

2.TMF: A GNSS Tropospheric Mapping Function for the Asymmetrical Neutral Atmosphere

2.1. Tropospheric Delay Asymmetry

The tropospheric delays’ asymmetry can be assessed visually by skyplots with the removal of the average value over all azimuths on each elevation angle. Due to space limitation, only a few of them are present here exemplarily to demonstrate the spatio-temporal variability. Figure 1 and Figure 2 are the IGS station SHAO results on 21 July and 26 December 2018, respectively. The epoch of the left and right panel is 0:00 UTC and 5:00 UTC, respectively.
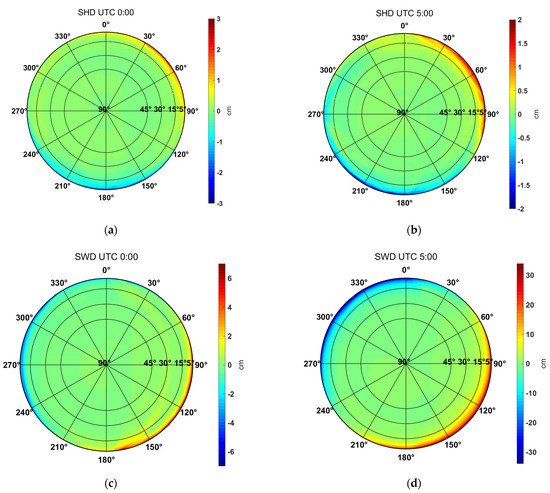
Remotesensing 13 02568 g007 550
Figure 1. The asymmetry of ray-tracing slant delays calculated by removal of the mean value of each elevation on all azimuths, for the IGS station SHAO located in Shanghai on 21 July 2018 (a) SHDs at 00:00 UTC, (b) SHDs at 05:00 UTC, (c) SWDs at 00:00 UTC, (d) SWDs at 05:00 UTC. Please note the difference between the bound of the colour bar on the right side of each subfigure.
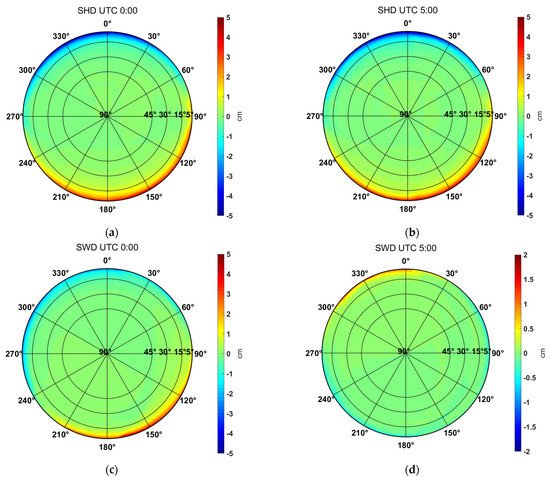
Remotesensing 13 02568 g008 550
Figure 2. The asymmetry of ray-tracing slant delays calculated by removal of the mean value of each elevation, for the IGS station SHAO located in Shanghai on 26 December 2018. (a) SHDs at 00:00 UTC, (b) SHDs at 05:00 UTC, (c) SWDs at 00:00 UTC, (d) SWDs at 05:00 UTC. Please note the difference between the bound of the colorbar.
Figure 1d shows much more significant anisotropy (please note the disparity in the bounds of the colour bars) than Figure 1c, which means that there was a quick variation of SWD from 0:00 to 5:00 UTC. This may be due to the fast-changing distribution of humidity, the typical summer weather conditions at Shanghai, where the SHAO station is located.
The situation is a little different on 26 December. As shown in Figure 2, although the elevation-dependent pattern is similar to Figure 2, SHD shows more spatial variability than SWD this time. The SHD range can reach up to ~10 cm at 5° elevation, while the SWD range is no more than several centimeters. This result may be caused by the fact that there is much less water vapor in winter than in summer in Shanghai. However, a comparison between Figure 2c,d shows that the temporal variations of SWD are still more complicated than SHD.
In order to get a more quantitative investigation on the results at low elevations, we summarise the statistical result of slant delays at four specific elevations: 5°, 10°, 15° and 20° in Table 1 and Table 2. There is much in common between the two tables. Firstly, the SHD and SWD and their range and RMS all tend to increase positively as elevation angle decreases. However, the SHD is always 6–15 times as large as the SWD. Secondly, the RMS of SHD and SWD at an elevation above 15° are mainly at the level of several millimetres. Furthermore, the RMS and range at the 5° elevation are always ten times as lager as that at the 20° elevation, both for SHD and SWD. Results above indicate that both the SHD and the SWD may present decametric asymmetry at low elevations.
Table 1. Representative ray-tracing slant delays for SHAO located in Shanghai on 21 July 2018.
UTC Elevation
Angle		 SHD (m) SWD (m)
Mean Range RMS Mean Range RMS
0:00 5° 23.135 0.040 0.012 3.515 0.119 0.037
10° 12.706 0.015 0.004 1.850 0.029 0.007
15° 8.703 0.007 0.002 1.255 0.018 0.004
20° 6.636 0.004 0.001 0.953 0.012 0.003
5:00 5° 23.102 0.039 0.011 3.894 0.678 0.245
10° 12.689 0.015 0.004 2.078 0.245 0.080
15° 8.691 0.007 0.002 1.410 0.118 0.037
20° 6.627 0.004 0.001 1.071 0.066 0.021
Table 2. Representative ray-tracing slant delays for SHAO located in Shanghai on 26 December 2018.
UTC Elevation
Angle		 SHD (m) SWD (m)
Mean Range RMS Mean Range RMS
  5° 23.525 0.100 0.034 1.632 0.075 0.026
0:00 10° 12.896 0.035 0.012 0.858 0.024 0.008
  15° 8.828 0.017 0.006 0.581 0.012 0.004
  20° 6.730 0.010 0.003 0.440 0.007 0.002
  5° 23.492 0.100 0.035 1.540 0.022 0.007
5:00 10° 12.876 0.036 0.012 0.806 0.005 0.001
  15° 8.814 0.019 0.006 0.545 0.003 0.001
  20° 6.719 0.011 0.003 0.414 0.002 0.000

2.2. TMF Fitting

The results of the four fitting schemes introduced in Table 1 are listed in Table 3, in which elevations are divided into two bands: low elevation  (3°≤θ≤15°) and high elevation (15°<θ<90°). As shown in Table 3, there is no apparent difference for bias and RMS between the two elevation and azimuth angle selection strategies (1 vs. 2, or 3 vs. 4). However, the horizontal resolution of ERA5 has a significant impact on the results. The RMS of the fitted SWDs based on ERA5 with 1° × 1° horizontal resolution is four and 7~9 times larger than that of the 0.25° × 0.25°, at low and high elevation angle bands, respectively. Results for SHD are similar but a little better. Hence, we use Scheme 2 in Table 1 (ERA5 with a horizontal resolution of 0.25° × 0.25°, at 18 selected elevations and 24 azimuths) to implement ray-tracing in the following research, which aims to keep a balance between the computational accuracy and the efficiency.
Table 3. Statistic result of TMF-derived slant delays, which are the product of the TMF and the ray-traced zenith delays. 
Elevation
Angle		 ΔSHD (cm)
bias1 RMS1 bias2 RMS2 bias3 RMS3 bias4 RMS4
3°–15° 0.0 0.3 0.0 0.3 −0.3 0.7 −0.3 0.7
15°–89° 0.0 0.0 0.0 0.1 −0.2 0.3 −0.2 0.3
Elevation
Angle		 ΔSWD (cm)
bias1 RMS1 bias2 RMS2 bias3 RMS3 bias4 RMS4
3°–15° 0.0 1.9 0.0 2.0 0.0 8.0 0.0 7.9
15°–89° 0.0 0.3 0.1 0.4 0.4 2.8 0.3 2.8

2.3. TMF Performance

The MF-derived slant delays are the production of the mapping factors and the ray-traced zenith delay. The discrepancy compared with the ray-traced slant delays can directly reflect the accuracy of a mapping function.
Figure 3 shows the RMS scatters of the discrepancies between MF-derived and ray-traced delays at the 5° elevation angle for the 12 globally distributed IGS stations listed in Table 1, at 96 epochs on four days (doy: 74, 202, 246, and 360) in 2018. Since each station’s computation is independent of each other, such a graph would be an excellent way to reflect the global applicability of a mapping function. As shown in Figure 3, the TMFabc performs the best globally, with RMS of almost the same level for each station. Notably, the station FAIR and YAKT have the highest accuracy of wet delays. This may be due to the cold and dry weather on high latitudes in the northern hemisphere.
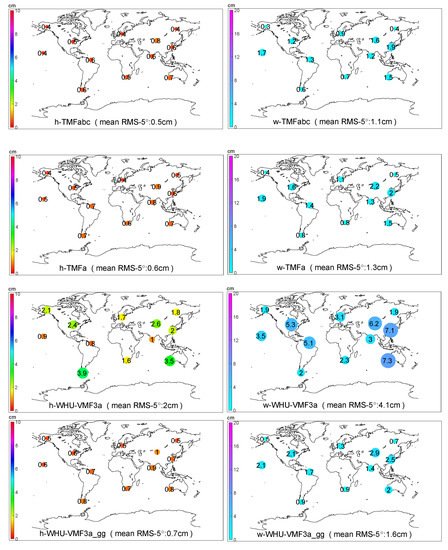
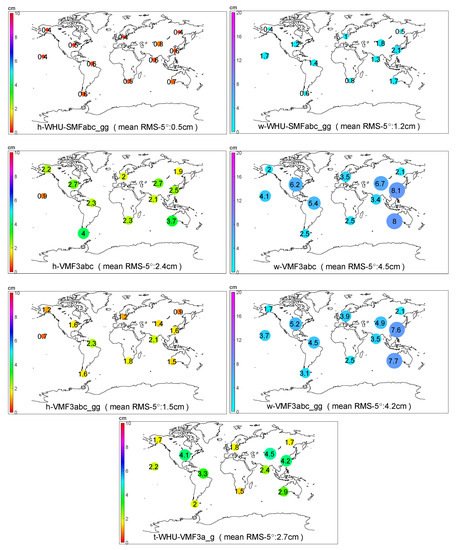
Remotesensing 13 02568 g009a 550Remotesensing 13 02568 g009b 550
Figure 3. The RMS of various mapping functions at the 5° elevation angle without or with gradients estimation for the 12 IGS stations on doy 74, 202, 246, and 360 in 2018. The size and the color of a circle denote the RMS5° value of the station, of which digit is also marked inside the circle.
In contrast, there are much more variations with the symmetric mapping functions based on the VMF3 concept (WHU-VMF3a, WHU-VMF3a_gg, and WHU-VMF3a_g), especially for the wet delays. However, comparing WHU-VMF3a_gg with WHU-VMF3a shows that the estimation of gradients improves the result dramatically, although not as good as that of TMFs.
The performances of the original VMF3 (VMF3abc and VMF3abc_gg) are the worst but not surprising since the resolution of the NWM used by us (0.25° × 0.25°, 137 model levels, 1 h) is superior to that of VMF3 (1° × 1°, 25 pressure levels, 6 h [40]). VMF3abc_gg improves accuracy mainly on hydrostatic delays but very slightly on wet delays. We can conclude that the resolution of the NWM limits the accuracy of VMF3-derived wet gradients.
TMFabc performs the best among all hydrostatic mapping functions, with the minimal RMSall (RMS for all elevation angles) and the minimal RMS5° (RMS for the 5° elevation angle). Compared with WHU-VMF3a, TMFabc improves the RMSall and the RMS5° by 68% and 74%, respectively. By the extra estimation of hydrostatic gradients, WHU-VMF3a_gg improves these by 62% and 65%, respectively. The accuracy of WHU-SMFabc_gg is only slightly lower than TMFabc. For VMF3, with gradients, the RMSall and the RMS5° can be improved by 35% and 39%, respectively. However, it seems that there are some slight systematic errors between the VMF3-derived and the WHURT-derived hydrostatic slant delays, which would be mainly due to the difference in the NWMs. By adopting the b and c coefficients of VMF3, TMFa can achieve higher accuracy than WHU-VMF3a_gg, with less computational cost than TMFabc, which could be meaningful for large-scale computing.
All MF-derived wet delays’ biases are closer to zero than the hydrostatic ones, but mostly with larger RMSs. TMFabc is still the most accurate, followed by the WHU-SMFabc_gg and TMFa. There is no significant difference between TMFabc and WHU-SMFabc_gg for most stations at most epochs, except for some particular conditions. Figure 4 shows this exemplarily for IGS station SHAO on the doy 202, 2018, when typhoon “Ampil” passed Shanghai. During 3:00–5:00 and 18:00–20:00 UTC, there are apparent improvements for TMFabc against WHU-SMF3abc_gg. WHU-VMF3a_gg improves the RMSall and the RMS5° of WHU-VMF3a by 59% and 62%, respectively.
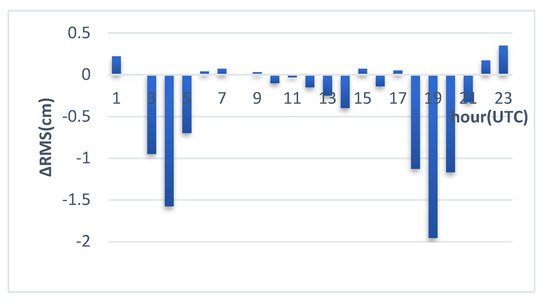
Remotesensing 13 02568 g010 550
Figure 4. The difference of RMS5° computed by w-TMFabc minus w-WHU-SMFabc_gg for station SHAO (Shanghai, China) for doy 202, 2018.
Figure 5 shows the RMS scatters of all kinds of MF-derived total delays at the 5° elevation angle, which are calculated by rmstotal=rms2h+rms2w−−−−−−−−−−−√, where rmsh, and rmsw are the RMS5° of the hydrostatic and wet MF-derived delays respectively. TMFabc performs the best. The improvement percentage of TMFabc against WHU-VMF3a, WHU-VMF3a_g, and WHU-VMF3a_gg can reach up to 73%, 54%, and 29%, respectively. Even by directly adopting the two coefficients b and c of VMF3 instead of estimating them, TMFa can still improve WHU-VMF3a, WHU-VMF3a_g WHU-VMF3a_gg by 68%, 47%, and 18%, respectively. It is worth noting that the improvement percentage of WHU-VMF3a_gg against WHU-VMF3a_g is 35%, which indicates that a separate estimation of the hydrostatic and wet gradients is preferable to a coarse estimation of the total gradients. Compared with WHU-VMF3a, the reduced RMS5° ratio between WHU-VMF3a_gg and TMFabc is 2.8/3.3, which is close to the value found by Landskron, et al. [46] that two-thirds of the azimuthal asymmetry can be described by the first-order gradients based on the VMF3 mapping function.
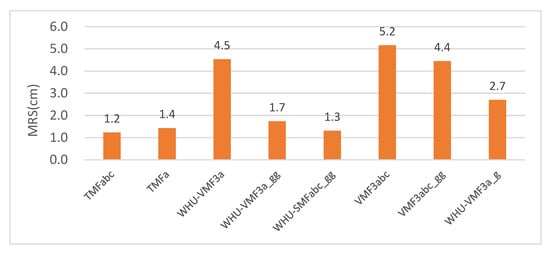
Remotesensing 13 02568 g011 550
Figure 5. The RMS scatters of MF-derived total delays at the 5° elevation angle (units: cm).

3. Discussion

Investigation of 360-degree ray-traced delays based on NWM revealed that both the SHD and SWD show azimuthal asymmetry, reaching up to decimeter level at low elevation angles below 15°. When a symmetric mapping function is used, the accuracy would not be as bad as expected, since the cutoff elevation angle is always set to 10° or 15° for most geodetic applications, which are typically based on double-differenced solutions. However, significant correlations between troposphere zenith delay parameters, station height, and receiver clock parameters are found [48]. The situation may be considerably improved by lowering the elevation cutoff angle. According to the rule of thumb, the delay path error at a 5° elevation will map to the station height at a ratio of 1/3 [34][36]. Therefore, it is essential to model variations of the slant delays on the elevation and the azimuth.
The gradient parameters have been used as a supplement for a symmetric mapping function to model the azimuthal asymmetry for decades. However, in former GNSS studies [43][44][45][51], only the total gradients can be estimated, due to the difficulty of distinguishing the hydrostatic and wet gradient mapping functions. The WHU-VMF3a_g can be deemed a simulation for such tropospheric delay strategy, of which accuracy is not as good as that of separate estimation of hydrostatic and wet gradients (WHU-VMF3a_gg). In contrast, TMF can achieve better accuracy than a VMF3-like symmetric mapping function enhanced by estimation of respective gradients, of which coefficients b and c are not estimated but obtained from climatology data, and a is determined at a single elevation angle. The result of SMFabc_gg indicates that: (1) If a symmetric mapping function is not accurate enough, it would be difficult to precisely model the anisotropy part of the tropospheric delays by gradients. Therefore, estimating coefficients by least-squares on sufficient widespread elevation angles is necessary. (2) Assuming a proper mapping function is applied, gradients can describe the bulk of the tilting troposphere in most situations. However, there could still be some non-negligible high-order residuals [46], especially under some particular conditions such as severe weather scenarios [62].
The assumption of a tilted troposphere can explain most of the actual distribution of the Earth’s troposphere. However, the tropospheric delay error of TMF is about ±1.2 cm at the 5° elevation angle, corresponding to a station height error of ±4 mm. A tilted troposphere may not fully explain the variability of the tropospheric delays, which is also affected by other factors, such as the highly variable water vapor. Therefore, further study should be investigated on how to model the residual delays more precisely based on TMF, if higher accuracy is required. Besides, various NWMs featuring high spatio-temporal resolution produced by different agencies could be utilized together to validate each other and achieve a more robust mapping function.

4. Conclusions

In this research, ERA5 data retrieved from ECMWF with the highest spatial-temporal resolution was applied to compute the tropospheric slant delays by the ray-tracing method. It is found that azimuthal variation of tropospheric delay at low elevation angles can reach up to several decimeters. Traditional three order continued fraction mapping functions have been developed based on the assumption of atmospheric spherical symmetry, in which the azimuthal variation of tropospheric delays is neglected. To overcome shortcomings caused by such mapping functions, TMF is built by tilting the zenith direction of the mapping function, of which coefficients were fitted by Levenberg–Marquardt nonlinear least square method. We found that the horizontal resolution of NWM has a significant impact on mapping functions. However, it is not necessary to choose all elevations and azimuths. Fitting at 18 selected elevations and 24 azimuths are proved to be enough to produce comparable results with complete sampling.
The performances of several mapping functions based on the TMF and VMF3 concept were assessed quantitatively by using the ray-traced slant delays as reference values. Results show that TMF can improve 54% against the VMF3-like symmetric mapping function enhanced by estimating total gradients (WHU-VMF3a_g). According to the rule of thumb, a similar improvement in height parameter estimation is expected in GNSS analysis, which needs to be verified in our further study. A global grid-wise TMF can be developed for an arbitrary station’s interpolation. To balance the accuracy and the computational cost, TMFa may be a good choice. Moreover, it would be necessary for the real-time application to derive TMF based on high-quality operational or forecast versions of NWM, including in-situ meteorological observations if possible.

References

  1. Yang, F.; Guo, J.; Meng, X.; Shi, J.; Xu, Y.; Zhang, D. Determination of Weighted Mean Temperature (Tm) Lapse Rate and Assessment of Its Impact on Tm Calculation. IEEE Access 2019, 7, 155028–155037.
  2. Zhang, D. The Study of the GNSS Tropospheric Zenith Delay Model and Mapping Function. Ph.D. Thesis, Wuhan University, Wuhan, China, 2017.
  3. Hopfield, H. Two-quartic tropospheric refractivity profile for correcting satellite data. J. Geophys. Res. 1969, 74, 4487–4499.
  4. Saastamoinen, J. Atmospheric correction for the troposphere and stratosphere in radio ranging satellites. Geophys. Monogr. Ser. 1972, 15, 247–251.
  5. Davis, J.; Herring, T.; Shapiro, I.; Rogers, A.; Elgered, G. Geodesy by radio interferometry: Effects of atmospheric modeling errors on estimates of baseline length. Radio Sci. 1985, 20, 1593–1607.
  6. Berrada Baby, H.; Gole, P.; Lavergnat, J. A model for the tropospheric excess path length of radio waves from surface meteorological measurements. Radio Sci. 1988, 23, 1023–1038.
  7. Ifadis, I.I. The Atmospheric Delay of Radio Waves: Modeling the Elevation Dependence on a Global Scale; Technical Report 38L; Chalmers University of Technology: GÄoteborg, Sweden, 1986.
  8. Askne, J.; Nordius, H. Estimation of tropospheric delay for microwaves from surface weather data. Radio Sci. 1987, 22, 379–386.
  9. Zhang, D.; Guo, J.; Chen, M.; Shi, J.; Zhou, L. Quantitative assessment of meteorological and tropospheric Zenith Hydrostatic Delay models. Adv. Space Res. 2016, 58, 1033–1043.
  10. COESA. U.S. Standard Atmosphere Supplements, 1966; U.S. Government Printing Office: Washington, DC, USA, 1966; pp. 101–102.
  11. Kirchengast, G.; Hafner, J.; Poetzi, W. The CIRA86aQ_UoG Model: An Extension of the CIRA-86 Monthly Tables Including Humidity Tables and a Fortran95 Global Moist Air Climatology Model; Institute for Meteorology and Geophysics, University of Graz: Graz, Austria, 1999; p. 18.
  12. Picone, J.; Hedin, A.; Drob, D.P.; Aikin, A. NRLMSISE-00 empirical model of the atmosphere: Statistical comparisons and scientific issues. JGR Space Phys. (1978–2012) 2002, 107, SIA 15-1–SIA 15-16.
  13. Leandro, R.; Santos, M.; Langley, R.B. UNB neutral atmosphere models: Development and performance. In Proceedings of the ION NTM, Monterey, CA, USA, 18–20 January 2006.
  14. Morris, A. Standard Temperature and Pressure. Ind. Heat. 2012, 80, 22.
  15. Böhm, J.; Möller, G.; Schindelegger, M.; Pain, G.; Weber, R. Development of an improved empirical model for slant delays in the troposphere (GPT2w). GPS Solut. 2015, 19, 433–441.
  16. Leandro, R.F.; Santos, M.C.; Langley, R.B. A North America wide area neutral atmosphere model for GNSS applications. Navigation 2009, 56, 57.
  17. RTCA. Minimum Operational Performance Standards for Global Positioning System/Wide Area Augmentation System Airborne Equipment; DO-229D; RTCA, Inc.: Washington, DC, USA, 13 December 2006; p. 564.
  18. Schüler, T. The TropGrid2 standard tropospheric correction model. GPS Solut. 2014, 18, 123–131.
  19. Yao, Y.; Xu, C.; Shi, J.; Cao, N.; Zhang, B.; Yang, J. ITG: A New Global GNSS Tropospheric Correction Model. Sci. Rep. 2015, 5, 10273.
  20. Li, W.; Yuan, Y.; Ou, J.; Chai, Y.; Li, Z.; Liou, Y.-A.; Wang, N. New versions of the BDS/GNSS zenith tropospheric delay model IGGtrop. J. Geod. 2015, 89, 73–80.
  21. Chen, J.P.; Wang, J.G.; Wang, A.H.; Ding, J.S.; Zhang, Y.Z. SHAtropE-A Regional Gridded ZTD Model for China and the Surrounding Areas. Remote Sens. 2020, 12, 165.
  22. Tralli, D.M.; Lichten, S.M. Stochastic estimation of tropospheric path delays in global positioning system geodetic measurements. Bull. Géodésique 1990, 64, 127–159.
  23. Webb, S.R. Kinematic GNSS Tropospheric Estimation and Mitigation over a Range of Altitudes. Ph.D. Thesis, Newcastle University, Newcastle, UK, 2015.
  24. Mousa, A.E.L.K.; Aboualy, N.; Sharaf, M.; Zahra, H.; Darrag, M. Tropospheric wet delay estimation using GNSS: Case study of a permanent network in Egypt. NRIAG J. Astron. Geophys. 2016, 5, 76–86.
  25. Dach, R.; Lutz, S.; Walser, P.; Fridez, P. Bernese GNSS Software Version 5.2; University of Bern: Bern, Switzerland, 2015; p. 854.
  26. Herring, T.A.; King, R.W.; Floyd, M.A.; McClusky, S.C. GAMIT Reference Manual Release 10.7; Massachusetts Institute of Technology: Cambridge, MA, USA, 2018; p. 168.
  27. Zhao, Q.; Yao, Y.; Yao, W.; Zhang, S. GNSS-derived PWV and comparison with radiosonde and ECMWF ERA-Interim data over mainland China. J. Atmos. Sol. Terr. Phys. 2018, 182, 85–92.
  28. He, Q.; Zhang, K.; Wu, S.; Shen, Z.; Wan, M.; Li, L. Precipitable Water Vapor Converted From GNSS-ZTD and ERA5 Datasets for the Monitoring of Tropical Cyclones. IEEE Access 2020, 8, 87275–87290.
  29. Yang, F.; Guo, J.; Meng, X.; Shi, J.; Zhang, D.; Zhao, Y. An improved weighted mean temperature (T-m) model based on GPT2w with T-m lapse rate. GPS Solut. 2020, 24.
  30. Barriot, J.-P.; Peng, F. Beyond Mapping Functions and Gradients; IntechOpen: London, UK, 2021.
  31. Marini, J.W. Correction of Satellite Tracking Data for an Arbitrary Tropospheric Profile. Radio Sci. 1972, 7, 223–231.
  32. Herring, T.A. Modeling Atmospheric Delays in the Analysis of Space Geodetic Data. In Refraction of Transatmospheric Signals in Geodesy; De Munck, J.C., Spoelstra, T.A., Eds.; The Netherlands Commission on Geodesy: Delft, The Netherlands, 1992.
  33. Niell, A.E. Global mapping functions for the atmosphere delay at radio wavelengths. J. Geophys. Res. [Solid Earth] 1996, 101, 3227–3246.
  34. Niell, A.E. Preliminary evaluation of atmospheric mapping functions based on numerical weather models. Phys. Chem. Earth Part A 2001, 26, 475–480.
  35. Guo, J.; Langley, R.B. A New Tropospheric Propagation Delay Mapping Function for Elevation Angles Down to 2 degrees. In Proceedings of the ION GPS 2003, Portland, OR, USA, 9–12 September 2003.
  36. Boehm, J.; Schuh, H. Vienna mapping functions in VLBI analyses. Geophys. Res. Lett. 2004, 31, 131–144.
  37. Boehm, J.; Niell, A.; Tregoning, P.; Schuh, H. Global Mapping Function (GMF): A new empirical mapping function based on numerical weather model data. Geophys. Res. Lett. 2006, 33, 4.
  38. Boehm, J.; Werl, B.; Schuh, H. Troposphere mapping functions for GPS and very long baseline interferometry from European Centre for Medium-Range Weather Forecasts operational analysis data. J. Geophys. Res. 2006, 111, B02406.
  39. Lagler, K.; Schindelegger, M.; Böhm, J.; Krásná, H.; Nilsson, T. GPT2: Empirical slant delay model for radio space geodetic techniques. Geophys. Res. Lett. 2013, 40, 1069–1073.
  40. Landskron, D.; Bohm, J. VMF3/GPT3: Refined discrete and empirical troposphere mapping functions. J. Geod. 2018, 92, 349–360.
  41. Zus, F.; Dick, G.; Dousa, J.; Wickert, J. Systematic errors of mapping functions which are based on the VMF1 concept. GPS Solut. 2015, 19, 277–286.
  42. Yuan, Y.B.; Holden, L.; Kealy, A.; Choy, S.; Hordyniec, P. Assessment of forecast Vienna Mapping Function 1 for real-time tropospheric delay modeling in GNSS. J. Geod. 2019, 93, 1501–1514.
  43. Qiu, C.; Wang, X.M.; Li, Z.S.; Zhang, S.T.; Li, H.B.; Zhang, J.L.; Yuan, H. The Performance of Different Mapping Functions and Gradient Models in the Determination of Slant Tropospheric Delay. Remote Sens. 2020, 12, 130.
  44. Chen, G.; Herring, T.A. Effects of atmospheric azimuthal asymmetry on the analysis of space geodetic data. J. Geophys. Res. Solid Earth 1997, 102, 20489–20502.
  45. Böhm, J.; Urquhart, L.; Steigenberger, P.; Heinkelmann, R.; Nafisi, V.; Schuh, H. A Priori Gradients in the Analysis of Space Geodetic Observations. In Reference Frames for Applications in Geosciences; Springer: Berlin/Heidelberg, Germany, 2013; pp. 105–109.
  46. Landskron, D.; Bohm, J. Refined discrete and empirical horizontal gradients in VLBI analysis. J. Geod. 2018, 92, 1387–1399.
  47. Bar-Sever, Y.E.; Kroger, P.M.; Borjesson, J.A. Estimating horizontal gradients of tropospheric path delay with a single GPS receiver. J. Geophys. Res. 1998, 103, 5019–5035.
  48. Rothacher, M.; Springer, T.A.; Schaer, S.; Beutler, G. Processing Strategies for Regional GPS Networks; Springer: Berlin/Heidelberg, Germany, 1998; pp. 93–100.
  49. Meindl, M.; Schaer, S.; Hugentobler, U.; Beutler, G. Tropospheric gradient estimation at CODE: Results from global solutions. J. Meteorol. Soc. Jpn. 2004, 82, 331–338.
  50. Lu, C.; Li, X.; Li, Z.; Heinkelmann, R.; Nilsson, T.; Dick, G.; Ge, M.; Schuh, H. GNSS tropospheric gradients with high temporal resolution and their effect on precise positioning. J. Geophys. Res. 2016, 121, 912–930.
  51. Iwabuchi, T.; Miyazaki, S.i.; Heki, K.; Naito, I.; Hatanaka, Y. An impact of estimating tropospheric delay gradients on tropospheric delay estimations in the summer using the Japanese nationwide GPS array. J. Geophys. Res. 2003, 108, 16.
  52. Zus, F.; Douša, J.; Kačmařík, M.; Václavovic, P.; Balidakis, K.; Dick, G.; Wickert, J. Improving GNSS Zenith Wet Delay Interpolation by Utilizing Tropospheric Gradients: Experiments with a Dense Station Network in Central Europe in the Warm Season. Remote Sens. 2019, 11, 674.
  53. Li, X.; Zus, F.; Lu, C.; Ning, T.; Dick, G.; Ge, M.; Wickert, J.; Schuh, H. Retrieving high-resolution tropospheric gradients from multiconstellation GNSS observations. Geophys. Res. Lett. 2015, 42, 4173–4181.
  54. Davis, J.L.; Elgered, G.; Niell, A.E.; Kuehn, C.E. Ground-based measurement of gradients in the “wet” radio refractivity of air. Radio Sci. 1993, 28, 1003–1018.
  55. Boehm, J.; Schuh, H. Troposphere gradients from the ECMWF in VLBI analysis. J. Geod. 2007, 81, 403–408.
  56. Li, X.; Dick, G.; Ge, M.; Heise, S.; Wickert, J.; Bender, M. Real-time GPS sensing of atmospheric water vapor: Precise point positioning with orbit, clock and phase delay corrections. Geophys. Res. Lett. 2014, 41, 3615–3621.
  57. Zhang, D. A building method for a troposphere mapping function model representing atmospheric anisotropy (patent of China). ZL201610831005.8, 19 September 2016.
  58. Zhang, F.; Barriot, J.P.; Xu, G.; Hopuare, M. Modeling the Slant Wet Delays From One GPS Receiver as a Series Expansion With Respect to Time and Space: Theory and an Example of Application for the Tahiti Island. IEEE Trans. Geosci. Remote Sens. 2020, 58, 7520–7532.
  59. Gardner, C.S. Correction of laser tracking data for the effects of horizontal refractivity gradients. Appl. Opt. 1977, 16, 2427–2432.
  60. Guo, J.; Zhang, D.; Shi, J.; Zhou, M. Using Ray-Tracing to Analyse the Precision of Three Classical Tropospheric Mapping Functions in China. Geomat. Inf. Sci. Wuhan Uni. 2015, 40, 182–187.
  61. Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Quart. J. R. Met. Soc. 2020, 146, 1999–2049.
  62. Masoumi, S.; McClusky, S.; Koulali, A.; Tregoning, P. A directional model of tropospheric horizontal gradients in Global Positioning System and its application for particular weather scenarios. J. Geophys. Res. 2017, 122, 4401–4425.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Remote Sensing
Contributor MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Di Zhang
View Times: 502
Revisions: 2 times (View History)
Update Date: 24 Nov 2021
Table of Contents
    1000/1000
    Hot Most Recent
    Feedback