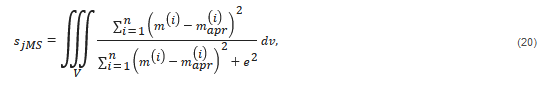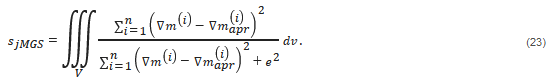1000/1000
Hot
Most Recent

Different geophysical methods provide information about various physical properties of rock formations and mineralization. In many cases, this information is mutually complementary. At the same time, inversion of the data for a particular survey is subject to considerable uncertainty and ambiguity as to causative body geometry and intrinsic physical property contrast. One productive approach to reducing uncertainty is to jointly invert several types of data. Non-uniqueness can also be reduced by incorporating additional information derived from available geological and/or geophysical data in the survey area to reduce the searching space for the solution. This additional information can be incorporated in the form of a joint inversion of multiphysics data.
Information from different surveys is mutually complementary, which makes it natural to consider a joint inversion of the data to a shared model, a process which can be implemented using several different physical and mathematical approaches. Integration of multiphysics data also helps reduce ambiguity, which is typical for geophysical inversions. Over the last decades, several approaches were introduced to joint inversion of geophysical data. The traditional technique is based on using the known petrophysical relationships between different physical properties of the rocks within the framework of the inversion process [1][2][3][4][5][6][7][8][9]. The joint inversion can use these relationships or can indicate and characterize the existence of this correlation, yielding an improved final model.
Another approach to joint inversion uses a clustering concept from statistics, which assumes that the subsurface geology can be described by the models with petrophysical parameters forming a specific number of the known clusters in the space of the models (e.g., [10][11][12]). This approach requires a priori knowledge of the parameters of these clusters, which is related to the lithology of the rocks.
Gramian constraints enforce the correlation between different parameters or their transforms [6][7]. They are implemented by using a Gramian mathematical operator in regularized inversion, which results in producing multimodal inverse solutions with enhanced correlations between the different model parameters or their attributes.
Let us consider forward geophysical problems for multiple geophysical data sets. These problems can be described by the following operator relationships:

Note that diverse model parameters may have different physical dimensions (e.g., density is measured in g/cm3, resistivity is measured in Ohm-m, etc.). It is convenient to introduce the dimensionless weighted model parameters, m ˜ ( i ) = W m ( i ) m ( i ) , where W m ( i ) is the corresponding linear operator of model weighting [7].
Joint inversion of multiphysics data can be reduced to minimization of the following parametric functional,

The selection of the model and data weights was discussed in many publications on inversion theory. For example, in the framework of the probabilistic approach [18], the weights were determined as inverse data covariance or model covariance matrices. In the framework of the deterministic approach [19], the weights were determined as inverse integrated sensitivity matrices.
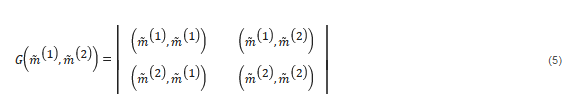



One of the most widely used approaches to imposing the structural constraints on the results of the joint inversion is based on the method of cross gradients [13][14][15][16][17]. The basic idea behind this method is that the gradients of the model parameters should be parallel in order to enforce the geometrical similarities between the interfaces of the models. Within the framework of the cross-gradient method, this requirement can be achieved by minimizing the norm square of the cross product of the gradients of these functions:

In the framework of the Gramian approach, the same requirement for the gradients of the model parameters being parallel is achieved by minimizing the structural Gramian functional, G ∇ , which, in a case of two physical properties, can be written using matrix notations, as follows:
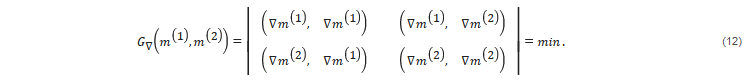

The constraints based on minimization of the Gramian of the model parameters, Equations (5) and (6), or of their gradients, Equations (12) and (13), can be treated as the global constraints, because they enforce similar correlation conditions over the entire inversion domain. In practical applications, however, the specific form of the correlations may vary within the area of investigation. To address this situation, we can subdivide the inversion domain, D, into N subdomains, D k , with potentially different types of relationships between the different model parameters, and define the Gramians, G k , for each of these subdomains separately:

In this case, the localized Gramian constraints will be based on using the following stabilizing functional:
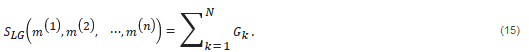
In a similar way, we can introduce localized Gramian-based structural constraints, using the localized Gramian of model parameter gradients, G ∇ k , defined by the following formula:
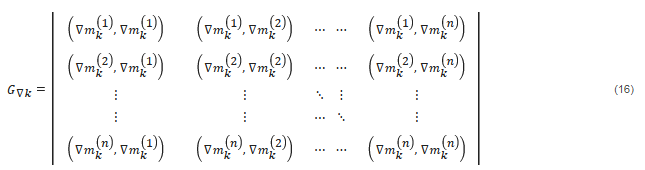
For example, in a case of two model parameters, localized Gramian (16) takes the form:

and the corresponding stabilizing functional is written as follows:

The structural similarities between various petrophysical models of the subsurface can be enforced by using the joint total variation or focusing stabilizers [21][22]. For the solution of a nonlinear inverse problem shown in Equation (1), following [21][22], we introduce the following parametric functional with focusing stabilizers,
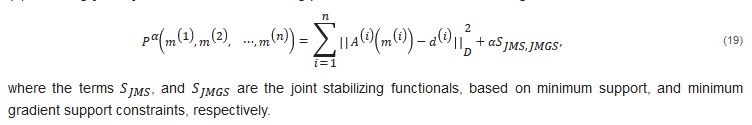
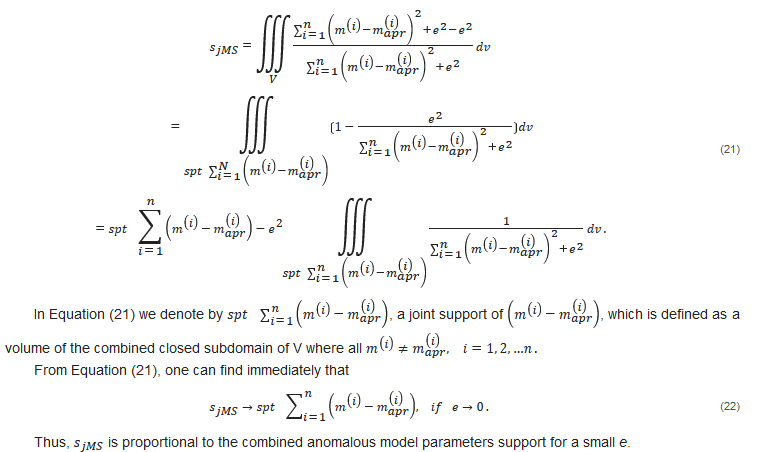
The joint minimum support stabilizer,