
Video Upload Options
Nucleation plays a vital role in polymer crystallization, in which chain connectivity and thus the multiple length and time scales make crystal nucleation of polymer chains an interesting but complex subject. Though the topic has been intensively studied in the past decades, there are still many open questions to answer. The final properties of semicrystalline polymer materials are affected by all of the following: the starting melt, paths of nucleation, organization of lamellar crystals and evolution of the final crystalline structures. In this viewpoint, we attempt to discuss some of the remaining open questions and corresponding concepts: non-equilibrated polymers, self-induced nucleation, microscopic kinetics of different processes, metastability of polymer lamellar crystals, hierarchical order and cooperativity involved in nucleation, etc. Addressing these open questions through a combination of novel concepts, new theories and advanced approaches provides a deeper understanding of the multifaceted process of crystal nucleation of polymers.
1. What Makes Nucleation of Polymer Crystals so Difficult?
2. Beyond Thermodynamic Concepts
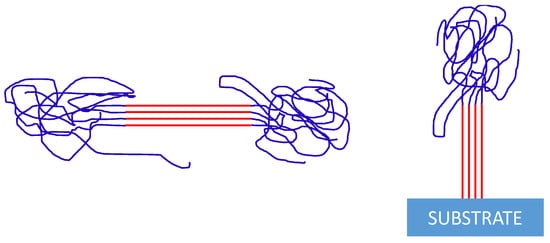
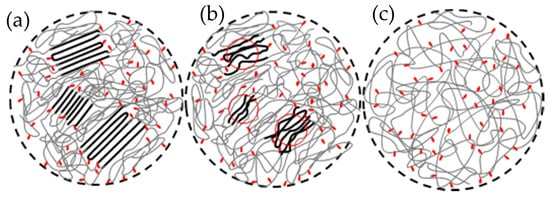
3. Nucleation from Non-Equilibrated Melts
References
- Wittmann, J.C.; Lotz, B. Epitaxial crystallization of polyethylene on organic substrates: A reappraisal of the mode of action of selected nucleating agents. J. Polym. Sci. Polym. Phys. Ed. 1981, 19, 1837–1851.
- Vidotto, G.; Levy, D.; Kovacs, A.J. Crystallization and fusion of self-seeding polymers. I. Poly-1-butene, polyethylene and polyoxyethylene of high molecular weight. Kolloid-Z. Z. Polym. 1969, 230, 289–305.
- Xu, J.; Ma, Y.; Hu, W.; Rehahn, M.; Reiter, G. Cloning polymer single crystals through self-seeding. Nat. Mater. 2009, 8, 348–353.
- Mauritz, K.A.; Baer, E.; Hopfinger, A.J. The epitaxial crystallization of macromolecules. J. Polym. Sci. Macromol. Rev. 1978, 13, 1–61.
- Xin, R.; Zhang, J.; Sun, X.; Li, H.; Qiu, Z.; Yan, S. Epitaxial Effects on Polymer Crystallization. Adv. Polym. Sci. 2015, 277, 55–94.
- Miller, R.L. Flow-Induced Crystallization in Polymer Systems; Gordon and Breach Science: New York, NY, USA, 1977.
- Li, L.; De Jeu, W.H. Flow-induced mesophases in crystallizable polymers. Interphases and Mesophases in Polymer Crystalli-zation II. Adv. Polym. Sci. 2005, 181, 75–120.
- Su, Z.; Dong, M.; Guo, Z.; Yu, J. Study of Polystyrene and Acrylonitrile-Styrene Copolymer as Special β-Nucleating Agents to Induce the Crystallization of Isotactic Polypropylene. Macromolecules 2007, 40, 4217–4224.
- Fillon, B.; Wittmann, J.C.; Lotz, B.; Thierry, A. Self-nucleation and recrystallization of isotactic polypropylene (α phase) investigated by differential scanning calorimetry. J. Polym. Sci. Part B Polym. Phys. 1993, 31, 1383–1393.
- Reid, B.O.; Vadlamudi, M.; Mamun, A.; Janani, H.; Gao, H.; Hu, W.; Alamo, R.G. Strong memory effect of crystallization above the equilibrium melting point of random copolymers. Macromolecules 2013, 46, 6485–6497.
- Mamun, A.; Chen, X.; Alamo, R.G. Interplay between a strong memory effect of crystallization and liquid-liquid phase sepa-ration in melts of broadly distributed ethylene-1-alkene copolymers. Macromolecules 2014, 47, 7958–7970.
- Sangroniz, L.; Cavallo, D.; Santamaria, A.; Müller, A.J.; Alamo, R.G. Thermo-rheologically complex self-seeded melts of pro-pylene-ethylene copolymers. Macromolecules 2017, 50, 642–651.
- Sangroniz, L.; Cavallo, D.; Müller, A.J. Self-Nucleation Effects on Polymer Crystallization. Macromolecules 2020, 53, 4581–4604.
- Fischer, E.W.; Schmidt, G.F. Long Periods in Drawn Polyethylene. Angew. Chem. Int. Ed. 1962, 1, 488–499.
- Chen, X.; Qu, C.; Alamo, R.G. Effect of annealing time and molecular weight on melt memory of random ethylene 1-butene copolymers. Polym. Int. 2019, 68, 248–256.
- Chen, X.; Mamun, A.; Alamo, R.G. Effect of level of crystallinity on melt memory above the equilibrium melting temperature in a random ethylene 1-butene copolymer. Macromol. Chem. Phys. 2015, 216, 1220–1226.
- Kovacs, A.J.; Gonthier, A. Crystallization and fusion of self-seeded polymers. 2. Growth-rate, morphology and isothermal thickening of single-crystals of low molecular-weight poly(ethylene-oxide) fractions. Kolloid-Z. Z. Polym. 1972, 250, 530–551.
- Keith, H.; Chen, W. On the origins of giant screw dislocations in polymer lamellae. Polymer 2002, 43, 6263–6272.
- Kaner, P.; Ruiz-Orta, C.; Boz, E.; Wagener, K.B.; Tasaki, M.; Tashiro, K.; Alamo, R.G. Kinetic Control of Chlorine Packing in Crystals of a Precisely Substituted Polyethylene. Toward Advanced Polyolefin Materials. Macromolecules 2013, 47, 236–245.
- Zhang, H.; Yu, M.; Zhang, B.; Reiter, R.; Vielhauer, M.; Mülhaupt, R.; Xu, J.; Reiter, G. Correlating Polymer Crystals via Self-Induced Nucleation. Phys. Rev. Lett. 2014, 112, 237801.
- Majumder, S.; Reiter, R.; Xu, J.; Reiter, G. Controlling the Growth of Stacks of Correlated Lamellar Crystals of a Block Copolymer. Macromolecules 2019, 52, 9665–9671.
- Majumder, S.; Poudel, P.; Zhang, H.; Xu, J.; Reiter, G. A nucleation mechanism leading to stacking of lamellar crystals in polymer thin films. Polym. Int. 2020, 69, 1058–1065.
- Subbotin, A.V.; Semenov, A.N. Phase Separation in Polymer Solutions under Extension. Polym. Sci. Ser. C 2018, 60, 106–117.
- Alfonso, G.C.; Ziabicki, A. Memory effects in isothermal crystallization II. Isotactic polypropylene. Colloid Polym. Sci. 1995, 273, 317–323.
- Zhang, Y.-S.; Zhong, L.-W.; Yang, S.; Liang, D.-H.; Chen, E.-Q. Memory effect on solution crystallization of high molecular weight poly (ethylene oxide). Polymer 2012, 53, 3621–3628.
- Mamun, A.; Umemoto, S.; Okui, N.; Ishihara, N. Self-Seeding Effect on Primary Nucleation of Isotactic Polystyrene. Macromolecules 2007, 40, 6296–6303.
- Lorenzo, A.T.; Arnal, M.L.; Sanchez, J.J.; Müller, A.J. Effect of annealing time on the self-nucleation behavior of semicrystal-line polymers. J. Polym. Sci. B Polym. Phys. 2006, 44, 1738–1750.
- Häfele, A.; Heck, B.; Hippler, T.; Kawai, T.; Kohn, P.; Strobl, G. Crystallization of poly(ethylene-co-octene): II Melt memory effects on first order kinetics. Eur. Phys. J. E 2005, 16, 217–224.
- Ergoz, E.; Fatou, J.G.; Mandelkern, L. Molecular Weight Dependence of the Crystallization Kinetics of Linear Polyethylene. I. Experimental Results. Macromolecules 1972, 5, 147–157.
- Supaphol, P.; Spruiell, J.E. Crystalline memory effects in isothermal crystallization of syndiotactic polypropylene. J. Appl. Polym. Sci. 2000, 75, 337–346.
- Hu, W.; Mathot, V.B.F.; Alamo, R.G.; Gao, H.; Chen, X. Crystallization of Statistical Copolymers. Adv. Polym. Sci. 2016, 276, 1–43.
- Gao, H.; Vadlamudi, M.; Alamo, R.G.; Hu, W. Monte Carlo simulations of strong memory effect of crystallization in random copolymers. Macromolecules 2013, 46, 6498–6506.
- Fernández-D’Arlas, B.; Balko, J.; Baumann, R.P.; Pöselt, E.; Dabbous, R.; Eling, B.; Thurn-Albrecht, T.; Müller, A.J. Tailoring the morphology and melting points of segmented thermoplastic polyurethanes by self-nucleation. Macromolecules 2016, 49, 7952–7964.
- Luo, C.; Sommer, J.-U. Frozen topology: Entanglements control nucleation and crystallization in polymers. Phys. Rev. Lett. 2014, 112, 195702.
- Maus, A.; Hempel, E.; Thurn-Albrecht, T.; Saalwaechter, K. Memory effect in isothermal crystallization of syndiotactic poly-propylene Role of melt structure and dynamics? Eur. Phys. J. E 2007, 23, 91–101.
- Hamad, F.G.; Colby, R.H.; Milner, S.T. Lifetime of Flow-Induced Precursors in Isotactic Polypropylene. Macromolecules 2015, 48, 7286–7299.
- Schamme, B.; Dargent, E.; Fernandez-Ballester, L. Effect of random ethylene comonomer on relaxation of flow-induced pre-cursors in isotactic polypropylene. Macromolecules 2017, 50, 6396–6403.
- Klein, J.; Briscoe, B.J. The diffusion of long-chain molecules through bulk polyethelene. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1979, 365, 53–73.
- Bartels, C.R.; Crist, B.; Graessley, W.W. Self-diffusion coefficient in melts of linear polymers: Chain length and temperature dependence for hydrogenated polybutadiene. Macromolecules 1984, 17, 2702–2708.
- Schuman, T.; Stepanov, E.V.; Nazarenko, S.; Capaccio, G.; Hiltner, A.; Baer, E. Interdiffusion of linear and branched poly-ethylene in microlayers studied via melting behavior. Macromolecules 1998, 31, 4551–4561.
- Tao, H.; Lodge, T.P.; Von Meerwall, E.D. Diffusivity and Viscosity of Concentrated Hydrogenated Polybutadiene Solutions. Macromolecules 2000, 33, 1747–1758.
- Muthukumar, M. Communication: Theory of melt-memory in polymer crystallization. J. Chem. Phys. 2016, 145, 031105.




