Directed Assembly of Particle-Polymer Composites: History
View Latest Version
Please note this is an old version of this entry, which may differ significantly from the current revision.
Subjects: Polymer Science
Contributor:
Jaime Juarez

Particle-polymer dispersions are ubiquitous in additive manufacturing (AM), where they are used as inks to create composite materials with applications to wearable sensors, energy storage materials, and actuation elements. It has been observed that directional alignment of the particle phase in the polymer dispersion can imbue the resulting composite material with enhanced mechanical, electrical, thermal or optical properties. 

  • directed assembly
  • additive manufacturing
  • external fields
  • 3D printing
  • particle-polymer composites

1. Introduction

Additive manufacturing (AM) is a method by which three-dimensional computer-aided designs (CAD) are fabricated without the need for process planning [1]. This process involves the layer-by-layer deposition of filament, powder, or liquid drops to translate the CAD drawing into a fully realized object. The AM industry generated a revenue of approximately 5.2 billion USD in 2015 [2]. This revenue includes a 769 million USD AM materials market that produces, in descending order of market share, photopolymers, laser-sintered powders, filaments, and metals. These materials are used to support a variety of AM technologies [3] that include 3D printing, stereolithography, laminated object manufacturing, and fused deposition modeling.
Among the materials available for use in AM applications, polymers represent 51% of the products produced by AM systems [2][4]. This fraction does not include the 29% of products that blend polymers and metals together to form composite AM materials. The ubiquity of polymers in the AM industry likely arises from their low cost and high production volume. The U.S. National Research Council reports that polymers, in the form of plastics, fibers, and rubber, are produced in the range of 71 billion pounds per year with a financial return approaching 0.50 USD per pound [5]. As a fundamental building block for AM applications, polymers have properties that can be tuned to achieve specific rheological behavior [6][7][8] or functionalities related to ionic conductivity [9][10][11][12], thermal conductivity [13][14][15], and magnetic [16][17][18] or dielectric [19][20][21] permittivity.
While some of these polymer functionalities can be achieved through chemical modification, an alternative method is to disperse filler micro- or nanoparticles in the polymer solution prior to processing or deposition by AM [22][23][24][25][26]. Inks based on particle-polymer dispersions can be used in the AM process to create compositionally graded composites [27][28] that serve to enhance the multi-material capabilities of finished products [29]. Tuning the AM process for particle-polymer dispersions influences composite properties such as flexibility, mechanical strength, toughness, and optical transparency [30][31][32]. These material properties are directly tied to the filler particle organization within the composite [33].
Directing the assembly of filler particles in a composite toward specifically organized arrangements or orientations enables the fabrication of materials which exhibit hierarchical functionality from the nanoscale to the macroscale [34]. Polymer composites that contain aligned filler particles exhibit increased elastic moduli as compared with composites where the filler particles are randomly arranged [35][36][37][38]. Particle-polymer composites with internal alignment also exhibit anisotropic responses to mechanical, thermal, electric, or magnetic inputs [39][40][41][42]. The anisotropy exhibited by the aligned particle-polymer composites can be used for a variety of emerging soft material applications, including wearable sensing devices [43][44][45], energy storage [46][47][48], artificial muscles [49][50][51], and soft robotics [52][53][54]. The alignment of filler particles used in these materials is often achieved by the application of external fields such as electric [55][56], magnetic [57][58], and acoustic fields [59][60][61].
It is the purpose of this review article to provide an overview of some of the types of external fields used to direct the assembly or alignment of filler particle-polymer dispersions. Figure 1 summarizes the transport mechanisms discussed in this review. Using external fields to tune the internal arrangement of filler particles is a pathway towards fabricating functionally graded particle-polymer composites. Achieving specific arrangements of filler particle distributions requires an understanding of how different directed assembly mechanisms operate. The forces associated with each of these mechanisms can favor different structures and a fundamental understanding of these forces serves as the basis for a paradigm in multi-material AM processing. The review concludes with a discussion of how external fields can contribute to specific filler particle arrangements that enhance intrinsic material properties (e.g., elastic modulus) or can be used as an actuator to improve AM process control.
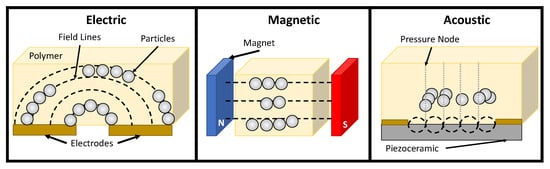
Micromachines 12 00935 g001 550
Figure 1. The diagram shows the three major types of external field mechanisms used in AM processing of particle-polymer composites.

2. Electric Fields

In uniform electric fields, or at low frequencies, particle transport is dominated by electrophoresis, which represents the migration of a charged particle towards an electrode of opposite polarity. The characteristic electrophoretic velocity as a function of frequency is [62][63]:
where b is the Stokes drag factor, εp is the dielectric constant of the particle, εo is the electric permittivity of free space, ζ is the particle zeta potential, E is the applied electric field, η is the medium viscosity, mp is the particle mass, and ω is the angular frequency of the field. Electrophoresis is frequently used to deposit colloidal particles onto surfaces to create functional materials by a process known as electrophoretic deposition [64][65].
In one demonstration of electrophoretic deposition for fabricating particle-polymer composites, poly [3-(3-N,N-diethylaminopropoxy)thiophene] (PDAOT) was dissolved in an acetic acid, water, and ethanol mixture [66]. The mixture was blended with a dispersion of single-wall carbon nanotubes (SWCNTs) and placed in an electrochemical cell, where a 3–15 V direct current (DC) potential was applied over a period of time that varied from 1 to 10 min. The process was used to control the particle-polymer deposition rate for the fabrication of metal oxide nanoparticle-polymer films with a thickness that varied from 100 nm to 15 μm [67][68]. Another polymer, poly (3-octylthiophene) (P3OT), has been blended with SWCNTs to fabricate particle-polymer films with enhanced current density [69]. In these experiments, a 40 V DC potential was applied to create a control particle-polymer film. An alternating current (AC) signal was superimposed onto the input DC signal, resulting in a 12% improvement to current density capacity. The current capacity of electrophoretically deposited particle-polymer films was used as the basis for a sensor which measured changes in resistivity due to in-plane shear stress [70].
Electrodes can also be patterned using photolithography to better concentrate deposition material. Electrode patterning allowed for the fabrication of a conductive particle-polymer film that resulted in a 344% improvement of current density as compared with films fabricated using a DC potential [69]. Photolithography has also been used as part of a process to create a substrate where electrophoretic deposition was applied to Ni fibers dispersed in a polyurethane-modified epoxy resin [71]. An unmodified resin was measured, and its Young’s modulus was 285 MPa after curing, while an electrophoretically deposited Ni fiber resin composite’s Young’s modulus was 6.8 GPa.
When a non-uniform electric field is used, particles migrate towards field minima or maxima depending on particle and medium properties [72][73][74]. This mechanism, known as dielectrophoresis, affects particles with a force that depends on the gradient of the applied electric field [75]:
where εm is the medium dielectric constant, Vp is the particle volume, and fcm is the Clausius–Mossotti factor. The parameter, fcm, is a factor that compares the relative contribution of particle and medium properties to the force acting on the particle. This contribution is as follows:

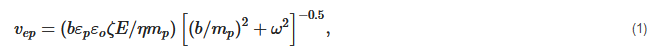
where the operator, Re, is used to find the real component of the Clausius–Mossotti term and ε˜=εεo−iσ/ω is the complex dielectric permittivity of the particle or the medium. In the DC limit, where ω = 0, fcm is dominated by conductivity values, while dielectric constants are important at high frequencies (ω→∞)[76].

Dipolar chains also form in response to electric field-induced polarization of the particles in solution. The dipolar chain energy acting on a single pair of particles in an electric field is [77]:

where p=3εmεoVpfcmE is the dipole moment of the particle pair, r is the center-to-center separation distance between particle pairs, P2 is a Legendre polynomial of order two, and θ is the angular orientation of the particle pair with respect to the direction of the applied electric field. The force representation of Equation (4) is [78]:

where er is a unit vector that connects the particle pair and ez is a unit vector that points in the direction of the electric field.
In uniform electric fields or electric fields with weak gradients, dipolar chain structures are observed in the resulting composite. These dipolar chains assemble with structures oriented in the primary direction of the applied electric field and, with particle loadings in sufficiently high concentrations, bridge the gap between electrodes, forming a percolated network. Spirulina, a microscopic organism with a spring-like structure, is coated with silver and dispersed in polydimethylsiloxane (PDMS) [79]. The Spirulina structures are used to create microcoils, as shown in Figure 2A. These microcoil particles assemble into chains between electrodes to form a composite with a conductivity of 10 S/m, which is eight orders of magnitude larger than non-aligned Spirulina samples (Figure 2B). Carbon nanocones dispersed in an acrylated urethane form chain structures that improve the electrical conductivity of the polymer from 10−7 to 10−3 S/m [80].
Micromachines 12 00935 g002 550
Figure 2. (A) SEM image of a metallic Spirulina-templated microcoil. The inset shows a cross-section of the microcoil particle; (B) the application of a 5 wt% electric field-aligned microcoil/PDMS composite in a functional LED integrated circuit. Reprinted with permission from [79], copyright 2017 American Chemical Society; optical micrographs showing (C) the top view and (D) side view of a thermally cured carbon nanocone film (0.2 vol%), which was assembled by DC field alignment; (E) inset shows an SEM image of the nanocone used in this process. Reprinted with permission from [80], copyright 2011 John Wiley and Sons; (F) hollow glass microspheres dispersed in Norland optical adhesive initially chain before (G) migrating towards an electrode. Reprinted with permission from [81], copyright 2017 Elsevier; (H) an acrylate polymer composite consisting of (I) SWCNT aligned using an AC electric field. Reprinted with permission from [82], copyright 2014 John Wiley and Sons.

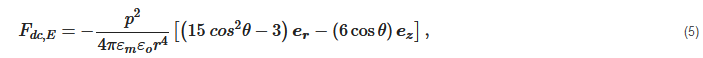
3. Magnetic Fields

Similar as with electric fields, particles respond to magnetic fields by migrating towards magnetic field minima or maxima depending on the intrinsic properties of the particle and the medium in which they are dispersed [83]. The magnetophoretic force responsible for this migration is given as follows:

where χp and χm are the magnetic susceptibilities of the particle and medium, respectively, and μo is the magnetic permeability of free space. The magnetic induction, B, is related to the applied magnetic field, H, by the expression [84] B=μo(1+χm)H. In addition to magnetophoresis, multiple particles also form dipolar chains in the direction of the magnetic field. The interaction energy between a single pair of particles in a magnetic field is [85]:

where m=(χp−χm)VpB/μo is the magnetic moment of the particle and θ is the angle the pair forms with respect to the direction of the magnetic field. The force representation of Equation (7) is [86]:

where er is a unit vector that connects the particle pair and ez is a unit vector that points in the direction of the magnetic field.
The use of magnets as a mechanism for composite fabrication has a long history due to the ease of the process and simplicity of blending para- or ferromagnetic particles with a polymer medium [87][88][89][90][91]. When magnetically sensitive particles are crosslinked in a polymer, the composite forms a magnetoelastomer that deforms in the presence of a magnetic field [92][93]. An alternative method for creating magnetoelastomers was suggested by the authors of this review [94]. In this alternative approach, a sacrificial scaffold was created in PDMS. The scaffold was dissolved, and a magnetorheological fluid was introduced to the evacuated channel, rendering the structure sensitive to magnetic field-induced deflections.
Magnetoelastic soft actuators (sometimes referred to as ferrogels) are designed by coupling magnetic properties of filler particles and elasticity of the polymer matrix. Understanding the deformation and mechanical properties of such actuators is crucial for optimizing their performance [95]. The deformation of these composites in the presence of a magnetic field is analogous to muscle constriction [96], which makes these types of composites ideal for actuation applications such as haptic control surfaces for steering [97].
Magnetite (Fe3O4) is one of the most frequently used filler material due to its high magnetic susceptibility [98], which makes it easy to pattern structures in polymers using externally directed magnetic fields [99]. Fe3O4 can be adsorbed on cellulose nanocrystals to fabricate magnetic cellulose nanocrystals (MGCNCs). The MGCNCs, shown in Figure 3, then are aligned in different configurations (parallel or perpendicular directions) in the polylactic acid matrix through a tunable magnetic field which result in fabrication of particle-polymer nanocomposite with anisotropic electrical and magnetic properties. The percent elongation improvement of the resulting nanocomposite is in the range of 60% to 240% [100]. This use of magnetic fields to locally pattern magnetite-PDMS composites led to a reduction in local elastic modulus by as much as 50% depending on filler particle concentration. While local elastic properties of the composite may see a reduction due to magnetic field-induced concentration, the bulk storage moduli of a magnetite-based composite are observed to increase by a factor of two depending on the field magnitude used to align particles [101]. Magnetite can also be functionally bound to materials that are not ferromagnetic, such as cellulose [102] or glass [103], to create materials with anisotropic mechanical properties or functional structures, like the circuit shown in Figure 4A,B.
Micromachines 12 00935 g003 550
Figure 3. Energy dispersive x-ray images show magnetic cellulose nanocrystals (MGCNC) without (A) an applied magnetic field, (B) a horizontally aligned magnetic field, and (C) a vertically aligned magnetic field. Insets diagrammatically show the field alignment for each case. Reprinted with permission from [103]. Copyright 2011 American Chemical Society.
Micromachines 12 00935 g004 550
Figure 4. A nanocomposite magnetic switch: (A) a gap between an aligned CNT coated composite and a nonmagnetic Pb is (B) closed when a magnet is placed underneath the Pb sheet, which lights an LED. Reprinted with permission from [102]. Copyright 2019 Elsevier. Environmental scanning electron microscopy images show the morphology of an epoxy composite sample processed at (C) no applied magnetic field and (D) at 15 T. The arrow represents the direction of the corresponding magnetic field. Reprinted with permission from [104]. Copyright 2004 John Wiley and Sons. (E) A complex pattern formed in a composite by the superposition of two separate magnetic fields. Reprinted with permission from [105]. Copyright 2017 Springer Nature.
Aside from magnetite, carbon nanotubes (CNTs) are also extensively used with magnetic fields to create aligned composites [106][107][108]. When a magnetic field is applied to anisotropic particle like CNT, the particle rotates with a torque of [109],

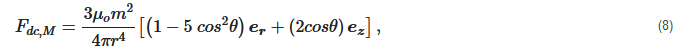
4. Acoustic Fields

An acoustic source, such as a piezeoelectric transducer, generates an acoustic radiation force that can be used to transport particles. The acoustic radiation force responsible for transporting particles is dependent on the gradient of the pressure field generated by the acoustic source [110][111][112]:

where β = 1/ρc2 is the compressibility, ρ is density, c is the speed of sound, Φ is the acoustic contrast factor, λ is the wavelength of the acoustic field, and P is the pressure distribution. The subscripts p and m refer to particle and medium properties, respectively. The pressure distribution for a one-dimensional standing wave is [113] P=Pocos(2πfx/cm), where Po is the pressure amplitude and f is the applied frequency.

Acoustic nodes are created when the acoustic wave is reflected. The resulting superposition of incident and reflected waves interfere with each other [114]. This phenomena, known as standing acoustic waves (SAW), has long been recognized as a method for separating small particles or drops dispersed in a fluid [110][115][116][117]. The relative difference in particle density and compressibility dictates whether particles migrate towards or away from the acoustic pressure node where the wave interference leads to a local pressure of zero. Particles that are more dense and less compressible than the medium, such as polystyrene [118] or cells [119], migrate to acoustic pressure nodes. Particles such as microbubbles [120] or PDMS [121] are less dense or more compressible than the medium in which they are dispersed, leading to migration towards the acoustic pressure antinode, where the pressure gradient is highest.

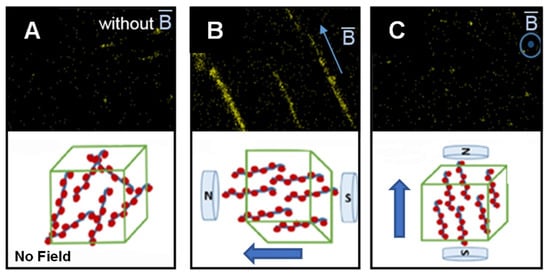
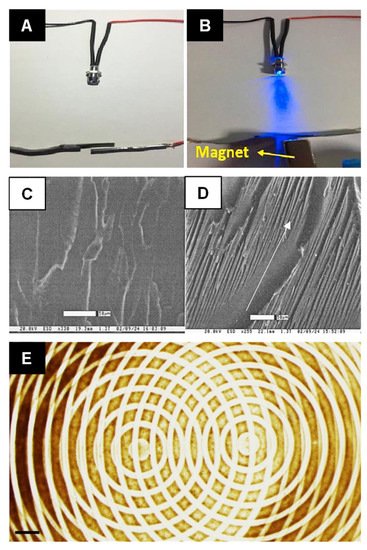
To demonstrate the utility of SAWs as a method for particle-polymer composite fabrication, early studies used polysiloxane as the polymer medium due to its ease of use and low cost [122]. The composite was prepared by blending the polysiloxane with a curing agent at a ratio of 20:1. Ten-micron acrylic spheres were dispersed in the polysiloxane fluid to act as filler particles. The acoustic field frequency was adjusted to create multiple acoustic nodes for filler particle assembly and allowed to set for 8 h. Adjusting the orientation and number of transducers can lead to different internal microstructures, such as lines or lattices [123]. Diffraction experiments showed that acoustic fields were excellent for localizing particles around the acoustic node [124]. Diamond nanoparticles with diameters of 5 nm were successfully arranged in ethanol-diluted epoxy matrix using acoustic standing wave to produce polymer nanocomposite. The radiation force of standing waves in a rectangular chamber was used to pattern clusters of nanoparticles. During the epoxy curing cycle of 5 min, the standing wave was activated and diamond nanoparticles migrated toward the nodes due to acoustic radiation force and formed quasi-parallel planes of particle clusters (Figure 5A) [125]. Complex particle-polymer composite structures can be formed using SAWs if the acoustic signal is first passed through a pattern that acts like a “hologram” for the desired structure (e.g., Figure 5B) [126][127][128].

Micromachines 12 00935 g005 550
Figure 5. (A) An X-ray microtomographic rendering of ~5 nm diamond nanoparticles assembled in an epoxy composite using a 1 MHz ultrasound standing wave. Reprinted with permission from [125], copyright 2011 AIP Publishing; (B) holographic tweezers used acoustic fields to assemble silicone particles to form complex, nonsymmetric structures. Reprinted with permission from [128], copyright 2011 John Wiley and Sons; (C, left) acoustically assembled fibers assembled at an acoustic node in an epoxy; (C, right) the composite is deposited on a substrate at a rate of 3.7 mm/s to form a printed line. Reprinted with permission from [129], copyright 2016 Elsevier; (D) lock (1 mm square) and key (200 μm circle) microgel assemble before excitation (left) and after acoustic excitation (right). Reprinted with permission from [130], copyright 2011 Elsevier; (E) iron oxide nanoparticles (50–100 nm) assemble in a hydrogel through vibrational excitation of the medium. Reprinted with permission from [60], copyright 2018 Elsevier.

This entry is adapted from the peer-reviewed paper 10.3390/mi12080935

References

  1. Gibson, I.; Rosen, D.W.; Stucker, B. Design for Additive Manufacturing. In Additive Manufacturing Technologies: Rapid Prototyping to Direct Digital Manufacturing; Gibson, I., Rosen, D.W., Stucker, B., Eds.; Springer US: Boston, MA, USA, 2010; pp. 299–332. ISBN 978-1-4419-1120-9.
  2. Wohlers Associates. Wohlers Report 2016: 3D Printing and Additive Manufacturing State of the Industry: Annual Worldwide Progress Report; Wohlers Associates: Fort Collins, CO, USA, 2016; ISBN 978-0-9913332-2-6.
  3. Wong, K.V.; Hernandez, A. A Review of Additive Manufacturing. Available online: https://www.hindawi.com/journals/isrn/2012/208760/ (accessed on 6 February 2019).
  4. Dizon, J.R.C.; Espera, A.H.; Chen, Q.; Advincula, R.C. Mechanical characterization of 3D-printed polymers. Addit. Manuf. 2018, 20, 44–67.
  5. National Research Council (U.S.). Polymer Science and Engineering: The Shifting Research Frontiers; National Academy Press: Washington, DC, USA, 1994; ISBN 978-0-309-04998-6.
  6. Siegel, J.E.; Erb, D.C.; Ehrenberg, I.M.; Jain, P.; Sarma, S.E. Local Viscosity Control Printing for High-Throughput Additive Manufacturing of Polymers. 3D Print. Addit. Manuf. 2016, 3, 252–261.
  7. Mackay, M.E. The importance of rheological behavior in the additive manufacturing technique material extrusion. J. Rheol. 2018, 62, 1549–1561.
  8. Cicala, G.; Giordano, D.; Tosto, C.; Filippone, G.; Recca, A.; Blanco, I. Polylactide (PLA) Filaments a Biobased Solution for Additive Manufacturing: Correlating Rheology and Thermomechanical Properties with Printing Quality. Materials 2018, 11, 1191.
  9. Schultz, A.R.; Lambert, P.M.; Chartrain, N.A.; Ruohoniemi, D.M.; Zhang, Z.; Jangu, C.; Zhang, M.; Williams, C.B.; Long, T.E. 3D Printing Phosphonium Ionic Liquid Networks with Mask Projection Microstereolithography. ACS Macro Lett. 2014, 3, 1205–1209.
  10. Karjalainen, E.; Wales, D.J.; Gunasekera, D.H.A.T.; Dupont, J.; Licence, P.; Wildman, R.D.; Sans, V. Tunable Ionic Control of Polymeric Films for Inkjet Based 3D Printing. ACS Sustain. Chem. Eng. 2018, 6, 3984–3991.
  11. Nulwala, H.; Mirjafari, A.; Zhou, X. Ionic liquids and poly(ionic liquid)s for 3D printing—A focused mini-review. Eur. Polym. J. 2018, 108, 390–398.
  12. Maciel, V.G.; Wales, D.J.; Seferin, M.; Sans, V. Environmental performance of 3D-Printing polymerisable ionic liquids. J. Clean. Prod. 2019, 214, 29–40.
  13. Bakarich, S.E.; Gorkin, R.; in het Panhuis, M.I.; Spinks, G.M. 4D Printing with Mechanically Robust, Thermally Actuating Hydrogels. Macromol. Rapid Commun. 2015, 36, 1211–1217.
  14. Zhao, Q.; Zou, W.; Luo, Y.; Xie, T. Shape memory polymer network with thermally distinct elasticity and plasticity. Sci. Adv. 2016, 2, e1501297.
  15. Kalsoom, U.; Peristyy, A.; Nesterenko, P.N.; Paull, B. A 3D printable diamond polymer composite: A novel material for fabrication of low cost thermally conducting devices. RSC Adv. 2016, 6, 38140–38147.
  16. Xia, H.; Wang, J.; Tian, Y.; Chen, Q.-D.; Du, X.-B.; Zhang, Y.-L.; He, Y.; Sun, H.-B. Ferrofluids for Fabrication of Remotely Controllable Micro-Nanomachines by Two-Photon Polymerization. Adv. Mater. 2010, 22, 3204–3207.
  17. Kokkinis, D.; Schaffner, M.; Studart, A.R. Multimaterial Magnetically Assisted 3D Printing of Composite Materials. Nat. Commun. 2015, 6, 8643.
  18. Huber, C.; Abert, C.; Bruckner, F.; Groenefeld, M.; Muthsam, O.; Schuschnigg, S.; Sirak, K.; Thanhoffer, R.; Teliban, I.; Vogler, C.; et al. 3D print of polymer bonded rare-earth magnets, and 3D magnetic field scanning with an end-user 3D printer. Appl. Phys. Lett. 2016, 109, 162401.
  19. Castles, F.; Isakov, D.; Lui, A.; Lei, Q.; Dancer, C.E.J.; Wang, Y.; Janurudin, J.M.; Speller, S.C.; Grovenor, C.R.M.; Grant, P.S. Microwave dielectric characterisation of 3D-printed BaTiO3/ABS polymer composites. Sci. Rep. 2016, 6, 22714.
  20. Yang, Y.; Chen, Z.; Song, X.; Zhu, B.; Hsiai, T.; Wu, P.-I.; Xiong, R.; Shi, J.; Chen, Y.; Zhou, Q.; et al. Three dimensional printing of high dielectric capacitor using projection based stereolithography method. Nano Energy 2016, 22, 414–421.
  21. Zhang, S.; Njoku, C.C.; Whittow, W.G.; Vardaxoglou, J.C. Novel 3D printed synthetic dielectric substrates. Microw. Opt. Technol. Lett. 2015, 57, 2344–2346.
  22. Debelak, B.; Lafdi, K. Use of exfoliated graphite filler to enhance polymer physical properties. Carbon 2007, 45, 1727–1734.
  23. Colombo, P.; Bernardo, E.; Parcianello, G. Multifunctional advanced ceramics from preceramic polymers and nano-sized active fillers. J. Eur. Ceram. Soc. 2013, 33, 453–469.
  24. de Leon, A.C.; Chen, Q.; Palaganas, N.B.; Palaganas, J.O.; Manapat, J.; Advincula, R.C. High performance polymer nanocomposites for additive manufacturing applications. React. Funct. Polym. 2016, 103, 141–155.
  25. Stansbury, J.W.; Idacavage, M.J. 3D printing with polymers: Challenges among expanding options and opportunities. Dent. Mater. 2016, 32, 54–64.
  26. Lebedev, S.M.; Gefle, O.S.; Amitov, E.T.; Berchuk, D.Y.; Zhuravlev, D.V. Poly(lactic acid)-based polymer composites with high electric and thermal conductivity and their characterization. Polym. Test. 2017, 58, 241–248.
  27. Kang, E.; Jeong, G.S.; Choi, Y.Y.; Lee, K.H.; Khademhosseini, A.; Lee, S.-H. Digitally tunable physicochemical coding of material composition and topography in continuous microfibres. Nat. Mater. 2011, 10, 877–883.
  28. Liu, W.; Zhang, Y.S.; Heinrich, M.A.; De Ferrari, F.; Jang, H.L.; Bakht, S.M.; Alvarez, M.M.; Yang, J.; Li, Y.-C.; Trujillo-de Santiago, G.; et al. Rapid Continuous Multimaterial Extrusion Bioprinting. Adv. Mater. 2017, 29, 1604630.
  29. Chung, D.D.L. A review of multifunctional polymer-matrix structural composites. Compos. Part B Eng. 2019, 160, 644–660.
  30. Vaezi, M.; Chianrabutra, S.; Mellor, B.; Yang, S. Multiple material additive manufacturing—Part 1: A review. Virtual Phys. Prototyp. 2013, 8, 19–50.
  31. Ge, Q.; Sakhaei, A.H.; Lee, H.; Dunn, C.K.; Fang, N.X.; Dunn, M.L. Multimaterial 4D Printing with Tailorable Shape Memory Polymers. Sci. Rep. 2016, 6, 31110.
  32. Bandyopadhyay, A.; Heer, B. Additive manufacturing of multi-material structures. Mater. Sci. Eng. R: Rep. 2018, 129, 1–16.
  33. Tsai, P.J.; Ghosh, S.; Wu, P.; Puri, I.K. Tailoring Material Stiffness by Filler Particle Organization. ACS Appl. Mater. Interfaces 2016, 8, 27449–27453.
  34. Holmes, L.R.; Riddick, J.C. Research Summary of an Additive Manufacturing Technology for the Fabrication of 3D Composites with Tailored Internal Structure. JOM 2014, 66, 270–274.
  35. Varga, Z.; Filipcsei, G.; Zrínyi, M. Magnetic field sensitive functional elastomers with tuneable elastic modulus. Polymer 2006, 47, 227–233.
  36. Sorrentino, L.; Aurilia, M.; Forte, G.; Iannace, S. Anisotropic mechanical behavior of magnetically oriented iron particle reinforced foams. J. Appl. Polym. Sci. 2011, 119, 1239–1247.
  37. Song, P.; Peng, Z.-J.; Yue, Y.-L.; Zhang, H.; Zhang, Z.; Fan, Y.-C. Mechanical properties of silicone composites reinforced with micron- and nano-sized magnetic particles. Express Polym. Lett. 2013, 7, 546–553.
  38. Compton, B.G.; Lewis, J.A. 3D-Printing of Lightweight Cellular Composites. Adv. Mater. 2014, 26, 5930–5935.
  39. Kimura, T.; Ago, H.; Tobita, M.; Ohshima, S.; Kyotani, M.; Yumura, M. Polymer Composites of Carbon Nanotubes Aligned by a Magnetic Field. Adv. Mater. 2002, 14, 1380–1383.
  40. Filipcsei, G.; Csetneki, I.; Szilágyi, A.; Zrínyi, M. Magnetic Field-Responsive Smart Polymer Composites. In Oligomers—Polymer Composites—Molecular Imprinting; Advances in Polymer Science; Springer: Berlin/Heidelberg, Germany, 2007; pp. 137–189. ISBN 9783540468295.
  41. Tomer, V.; Randall, C.A.; Polizos, G.; Kostelnick, J.; Manias, E. High- and low-field dielectric characteristics of dielectrophoretically aligned ceramic/polymer nanocomposites. J. Appl. Phys. 2008, 103, 034115.
  42. Tanimoto, M.; Yamagata, T.; Miyata, K.; Ando, S. Anisotropic Thermal Diffusivity of Hexagonal Boron Nitride-Filled Polyimide Films: Effects of Filler Particle Size, Aggregation, Orientation, and Polymer Chain Rigidity. ACS Appl. Mater. Interfaces 2013, 5, 4374–4382.
  43. Lipomi, D.J.; Vosgueritchian, M.; Tee, B.C.-K.; Hellstrom, S.L.; Lee, J.A.; Fox, C.H.; Bao, Z. Skin-like pressure and strain sensors based on transparent elastic films of carbon nanotubes. Nat. Nanotechnol. 2011, 6, 788–792.
  44. Lee, S.; Shin, S.; Lee, S.; Seo, J.; Lee, J.; Son, S.; Cho, H.J.; Algadi, H.; Al-Sayari, S.; Kim, D.E.; et al. Ag Nanowire Reinforced Highly Stretchable Conductive Fibers for Wearable Electronics. Adv. Funct. Mater. 2015, 25, 3114–3121.
  45. Lv, T.; Yao, Y.; Li, N.; Chen, T. Wearable fiber-shaped energy conversion and storage devices based on aligned carbon nanotubes. Nano Today 2016, 11, 644–660.
  46. Weng, W.; Sun, Q.; Zhang, Y.; Lin, H.; Ren, J.; Lu, X.; Wang, M.; Peng, H. Winding Aligned Carbon Nanotube Composite Yarns into Coaxial Fiber Full Batteries with High Performances. Nano Lett. 2014, 14, 3432–3438.
  47. Zhang, M.; Gao, T.; Wang, J.; Liao, J.; Qiu, Y.; Xue, H.; Shi, Z.; Xiong, Z.; Chen, L. Single BaTiO3 nanowires-polymer fiber based nanogenerator. Nano Energy 2015, 11, 510–517.
  48. Pan, S.; Lin, H.; Deng, J.; Chen, P.; Chen, X.; Yang, Z.; Peng, H. Novel Wearable Energy Devices Based on Aligned Carbon Nanotube Fiber Textiles. Adv. Energy Mater. 2015, 5, 1401438.
  49. Martin, J.E.; Anderson, R.A. Electrostriction in field-structured composites: Basis for a fast artificial muscle? J. Chem. Phys. 1999, 111, 4273–4280.
  50. Mirfakhrai, T.; Madden, J.D.W.; Baughman, R.H. Polymer artificial muscles. Mater. Today 2007, 10, 30–38.
  51. Chun, K.-Y.; Hyeong Kim, S.; Kyoon Shin, M.; Hoon Kwon, C.; Park, J.; Tae Kim, Y.; Spinks, G.M.; Lima, M.D.; Haines, C.S.; Baughman, R.H.; et al. Hybrid carbon nanotube yarn artificial muscle inspired by spider dragline silk. Nat. Commun. 2014, 5, 3322.
  52. Morales, D.; Bharti, B.; Dickey, M.D.; Velev, O.D. Bending of Responsive Hydrogel Sheets Guided by Field-Assembled Microparticle Endoskeleton Structures. Small 2016, 12, 2283–2290.
  53. Schmauch, M.M.; Mishra, S.R.; Evans, B.A.; Velev, O.D.; Tracy, J.B. Chained Iron Microparticles for Directionally Controlled Actuation of Soft Robots. ACS Appl. Mater. Interfaces 2017, 9, 11895–11901.
  54. Tognato, R.; Armiento, A.R.; Bonfrate, V.; Levato, R.; Malda, J.; Alini, M.; Eglin, D.; Giancane, G.; Serra, T. A Stimuli-Responsive Nanocomposite for 3D Anisotropic Cell-Guidance and Magnetic Soft Robotics. Adv. Funct. Mater. 2019, 29, 1804647.
  55. Fu, M.; Chaudhary, K.; Lange, J.G.; Kim, H.S.; Juárez, J.J.; Lewis, J.A.; Braun, P.V. Anisotropic Colloidal Templating of 3D Ceramic, Semiconducting, Metallic, and Polymeric Architectures. Adv. Mater. 2014, 26, 1740–1745.
  56. Wang, H.; Zhang, H.; Zhao, W.; Zhang, W.; Chen, G. Preparation of polymer/oriented graphite nanosheet composite by electric field-inducement. Compos. Sci. Technol. 2008, 68, 238–243.
  57. Fragouli, D.; Buonsanti, R.; Bertoni, G.; Sangregorio, C.; Innocenti, C.; Falqui, A.; Gatteschi, D.; Cozzoli, P.D.; Athanassiou, A.; Cingolani, R. Dynamical Formation of Spatially Localized Arrays of Aligned Nanowires in Plastic Films with Magnetic Anisotropy. ACS Nano 2010, 4, 1873–1878.
  58. Erb, R.M.; Libanori, R.; Rothfuchs, N.; Studart, A.R. Composites Reinforced in Three Dimensions by Using Low Magnetic Fields. Science 2012, 335, 199–204.
  59. Scholz, M.-S.; Drinkwater, B.W.; Trask, R.S. Ultrasonic assembly of anisotropic short fibre reinforced composites. Ultrasonics 2014, 54, 1015–1019.
  60. Shabaniverki, S.; Thorud, S.; Juárez, J.J. Vibrationally directed assembly of micro- and nanoparticle-polymer composites. Chem. Eng. Sci. 2018, 192, 1209–1217.
  61. Akella, M.; Juárez, J.J. High-Throughput Acoustofluidic Self-Assembly of Colloidal Crystals. ACS Omega 2018, 3, 1425–1436.
  62. O’Brien, R.W. Electro-acoustic effects in a dilute suspension of spherical-particles. J. Fluid Mech. 1988, 190, 71–86.
  63. Bahukudumbi, P.; Everett, W.N.; Beskok, A.; Bevan, M.A.; Huff, G.H.; Lagoudas, D.; Ounaies, Z. Colloidal microstructures, transport, and impedance properties within interfacial microelectrodes. Appl. Phys. Lett. 2007, 90, 224102–224103.
  64. Ammam, M. Electrophoretic deposition under modulated electric fields: A review. RSC Adv. 2012, 2, 7633–7647.
  65. Neirinck, B.; Van Der Biest, O.; Vleugels, J. A Current Opinion on Electrophoretic Deposition in Pulsed and Alternating Fields. J. Phys. Chem. B 2013, 117, 1516–1526.
  66. Wu, K.; Imin, P.; Adronov, A.; Zhitomirsky, I. Electrophoretic deposition of poly [3 -(3-N,N-diethylaminopropoxy)thiophene] and composite films. Mater. Chem. Phys. 2011, 125, 210–218.
  67. Yang, L.; Pang, X.; Fox-Rabinovich, G.; Veldhuis, S.; Zhitomirsky, I. Electrophoretic deposition of polymer and composite films. Surf. Eng. 2012, 28, 585–589.
  68. Sun, Y.; Ata, M.S.; Zhitomirsky, I. Electrophoretic deposition of linear polyethylenimine and composite films. Surf. Eng. 2013, 29, 495–499.
  69. Itoh, E.; Suzuki, I.; Miyairi, K. Field Emission from Carbon-Nanotube-Dispersed Conducting Polymer Thin Film and Its Application to Photovoltaic Devices. Jpn. J. Appl. Phys. 2005, 44, 636.
  70. An, Q.; Rider, A.N.; Thostenson, E.T. Hierarchical Composite Structures Prepared by Electrophoretic Deposition of Carbon Nanotubes onto Glass Fibers. ACS Appl. Mater. Interfaces 2013, 5, 2022–2032.
  71. Yang, Z.; Wang, H.; Zhang, Z.; Ding, G.; Zhao, X. Microtensile test of an ordered-reinforced electrophoretic polymer matrix composite fabricated by surface micromachining. Surf. Rev. Lett. 2011, 18, 169–175.
  72. Morgan, H.; Green, N.G. AC Electrokinetic: Colloids and Nanoparticles, 1st ed.; Research Studies Pr: Philadelphia, PA, USA, 2002; ISBN 978-0-86380-255-3.
  73. Juárez, J.J.; Cui, J.-Q.; Liu, B.G.; Bevan, M.A. kT-Scale Colloidal Interactions in High Frequency Inhomogeneous AC Electric Fields. I. Single Particles. Langmuir 2011, 27, 9211–9218.
  74. Juárez, J.J.; Liu, B.G.; Cui, J.-Q.; Bevan, M.A. kT-Scale Colloidal Interactions in High-Frequency Inhomogeneous AC Electric Fields. II. Concentrated Ensembles. Langmuir 2011, 27, 9219–9226.
  75. Pethig, R. Dielectrophoresis: Status of the Theory, Technology, and Applications. Biomicrofluidics 2010, 4, 022811.
  76. Jones, T.B. Electromechanics of Particles; Cambridge University Press: Cambridge, UK, 1995; ISBN 0521431964.
  77. Adriani, P.M.; Gast, A.P. A microscopic model of electrorheology. Phys. Fluids 1988, 31, 2757–2768.
  78. Whittle, M. Computer simulation of an electrorheological fluid. J. Non-Newton. Fluid Mech. 1990, 37, 233–263.
  79. Li, X.; Cai, J.; Shi, Y.; Yue, Y.; Zhang, D. Remarkable Conductive Anisotropy of Metallic Microcoil/PDMS Composites Made by Electric Field Induced Alignment. ACS Appl. Mater. Interfaces 2017, 9, 1593–1601.
  80. Knaapila, M.; Høyer, H.; Svåsand, E.; Buchanan, M.; Skjeltorp, A.T.; Helgesen, G. Aligned carbon cones in free-standing UV-Curable polymer composite. J. Polym. Sci. Part B Polym. Phys. 2011, 49, 399–403.
  81. Liu, X.; Liu, J.; Guo, Y.; Cakmak, M. Electric field assisted gradient structure formation of glass microsphere columns in polymer films. Compos. Sci. Technol. 2017, 153, 62–70.
  82. Sengezer, E.C.; Seidel, G.D.; Bodnar, R.J. Phenomenological characterization of fabrication of aligned pristine-SWNT and COOH-SWNT nanocomposites via dielectrophoresis under AC electric field. Polym. Compos. 2015, 36, 1266–1279.
  83. Pethig, R.R. Dielectrophoresis: Theory, Methodology and Biological Applications, 1st ed.; Wiley: Hoboken, NJ, USA, 2017.
  84. McHenry, M.E.; Laughlin, D.E. Magnetic Moment and Magnetization. In Characterization of Materials; Wiley: Hoboken, NJ, USA, 2012; pp. 1–25. ISBN 9780471266969.
  85. Furst, E.M.; Gast, A.P. Micromechanics of magnetorheological suspensions. Phys. Rev. E 2000, 61, 6732.
  86. Ji, D.; Luo, Y.; Ren, H.; Wei, D.; Shao, J. Numerical Simulation and Experimental Analysis of Microstructure of Magnetorheological Fluid. J. Nanomater. 2019, 2019, 6312606.
  87. Ginder, J.M.; Nichols, M.E.; Elie, L.D.; Tardiff, J.L. Magnetorheological elastomers: Properties and applications. In Smart Structures and Materials: Smart Materials Technologies; International Society for Optics and Photonics: Bellingham, WA, USA, 1999; Volume 3675, pp. 131–138.
  88. Jolly, M.R.; Bender, J.W.; Carlson, J.D. Properties and Applications of Commercial Magnetorheological Fluids. J. Intell. Mater. Syst. Struct. 1999, 10, 5–13.
  89. Sauzedde, F.; Elaïssari, A.; Pichot, C. Hydrophilic magnetic polymer latexes. Adsorption of magnetic iron oxide nanoparticles onto various cationic latexes. Colloid Polym. Sci. 1999, 277, 846–855.
  90. Shiga, T.; Okada, A.; Kurauchi, T. Magnetroviscoelastic behavior of composite gels. J. Appl. Polym. Sci. 1995, 58, 787–792.
  91. Shiga, T.; Okada, A.; Kurauchi, T. Electroviscoelastic effect of polymer blends consisting of silicone elastomer and semiconducting polymer particles. Macromolecules 1993, 26, 6958–6963.
  92. Zrínyi, M.; Barsi, L.; Büki, A. Deformation of ferrogels induced by nonuniform magnetic fields. J. Chem. Phys. 1996, 104, 8750–8756.
  93. Zrinyi, M.; Barsi, L.; Szabó, D.; Kilian, H.-G. Direct observation of abrupt shape transition in ferrogels induced by nonuniform magnetic field. J. Chem. Phys. 1997, 106, 5685–5692.
  94. Shabaniverki, S.; Xie, S.; Ren, J.; Juárez, J.J. Soft Ferrofluid Actuator Based on 3D-Printed Scaffold Removal. 3D Print. Addit. Manuf. 2021, 8, 126–135.
  95. Snyder, R.L.; Nguyen, V.Q.; Ramanujan, R.V. Design parameters for magneto-elastic soft actuators. Smart Mater. Struct. 2010, 19, 055017.
  96. Zrínyi, M. Intelligent polymer gels controlled by magnetic fields. Colloid Polym. Sci. 2000, 278, 98–103.
  97. Hatzfeld, C.; Bilz, J.; Fritzsche, T.; Kupnik, M. A Reconfigurable Haptic Joystick Based on Magneto-Rheological Elastomers—System Design and First Evaluation. In Haptics: Perception, Devices, Control, and Applications; Bello, F., Kajimoto, H., Visell, Y., Eds.; Springer International Publishing: London, UK, 2016; pp. 109–119.
  98. Wu, W.; He, Q.; Jiang, C. Magnetic Iron Oxide Nanoparticles: Synthesis and Surface Functionalization Strategies. Nanoscale Res. Lett. 2008, 3, 397–415.
  99. Ghosh, S.; Puri, I.K. Soft polymer magnetic nanocomposites: Microstructure patterning by magnetophoretic transport and self-assembly. Soft Matter 2013, 9, 2024–2029.
  100. Dhar, P.; Kumar, A.; Katiyar, V. Magnetic Cellulose Nanocrystal Based Anisotropic Polylactic Acid Nanocomposite Films: Influence on Electrical, Magnetic, Thermal, and Mechanical Properties. ACS Appl. Mater. Interfaces 2016, 8, 18393–18409.
  101. Kwon, S.H.; Lee, C.J.; Choi, H.J.; Chung, K.H.; Jung, J.H. Viscoelastic and mechanical behaviors of magneto-rheological carbonyl iron/natural rubber composites with magnetic iron oxide nanoparticle. Smart Mater. Struct. 2019, 28, 045012.
  102. Cao, L.; Cheng, Z.; Yan, M.; Chen, Y. Anisotropic rubber nanocomposites via magnetic-induced alignment of Fe3O4/cellulose nanocrystals hybrids obtained by templated assembly. Chem. Eng. J. 2019, 363, 203–212.
  103. Goldberg, O.; Greenfeld, I.; Wagner, H.D. Composite Reinforcement by Magnetic Control of Fiber Density and Orientation. ACS Appl. Mater. Interfaces 2018, 10, 16802–16811.
  104. Al-Haik, M.S.; Garmestani, H.; Li, D.S.; Hussaini, M.Y.; Sablin, S.S.; Tannenbaum, R.; Dahmen, K. Mechanical properties of magnetically oriented epoxy. J. Polym. Sci. Part B Polym. Phys. 2004, 42, 1586–1600.
  105. Yang, Z.; Wei, J.; Gizynski, K.; Song, M.-G.; Grzybowski, B.A. Interference-like patterns of static magnetic fields imprinted into polymer/nanoparticle composites. Nat. Commun. 2017, 8, 1564.
  106. Garmestani, H.; Al-Haik, M.S.; Dahmen, K.; Tannenbaum, R.; Li, D.; Sablin, S.S.; Hussaini, M.Y. Polymer-Mediated Alignment of Carbon Nanotubes under High Magnetic Fields. Adv. Mater. 2003, 15, 1918–1921.
  107. Goh, P.S.; Ismail, A.F.; Ng, B.C. Directional alignment of carbon nanotubes in polymer matrices: Contemporary approaches and future advances. Compos. Part A Appl. Sci. Manuf. 2014, 56, 103–126.
  108. Wu, S.; Peng, S.; Wang, C.H. Multifunctional Polymer Nanocomposites Reinforced by Aligned Carbon Nanomaterials. Polymers (Basel) 2018, 10, 542.
  109. Ranzoni, A.; Janssen, X.J.A.; Ovsyanko, M.; Van Ijzendoorn, L.J.; Prins, M.W.J. Magnetically controlled rotation and torque of uniaxial microactuators for lab-on-a-chip applications. Lab Chip 2009, 10, 179–188.
  110. King, L.V. On the Acoustic Radiation Pressure on Spheres. R. Soc. Lond. A Math. Phys. Sci. 1934, 147, 212.
  111. Laurell, T.; Petersson, F.; Nilsson, A. Chip integrated strategies for acoustic separation and manipulation of cells and particles. Chem. Soc. Rev. 2007, 36, 492–506.
  112. Bruus, H. Acoustofluidics 7: The acoustic radiation force on small particles. Lab Chip 2012, 12, 1014–1021.
  113. Owens, C.E.; Shields, C.W.; Cruz, D.F.; Charbonneau, P.; López, G.P. Highly parallel acoustic assembly of microparticles into well-ordered colloidal crystallites. Soft Matter 2016, 12, 717–728.
  114. Pain, H.J.; Rankin, P. Introduction to Vibrations and Waves; Wiley: Hoboken, NJ, USA, 2015; ISBN 978-1-118-69838-9.
  115. Söllner, K.; Bondy, C. The mechanism of coagulation by ultrasonic waves. Trans. Faraday Soc. 1936, 32, 616–623.
  116. Yosioka, K.; Kawasima, Y. Acoustic Radiation Pressure on a Compressible Spherical. Acustica 1955, 5, 167–173.
  117. Gor’kov, L.P. On the Forces Acting on a Small Particle in an Acoustical Field in an Ideal Fluid. Soviet Phys. Doklady 1962, 6, 773.
  118. Kalb, D.M.; Fencl, F.A.; Woods, T.A.; Swanson, A.; Maestas, G.C.; Juárez, J.J.; Edwards, B.S.; Shreve, A.P.; Graves, S.W. Line-Focused Optical Excitation of Parallel Acoustic Focused Sample Streams for High Volumetric and Analytical Rate Flow Cytometry. Anal. Chem. 2017, 89, 9967–9975.
  119. Shi, J.; Ahmed, D.; Mao, X.; Steven Lin, S.-C.; Lawit, A.; Jun Huang, T. Acoustic tweezers: Patterning cells and microparticles using standing surface acoustic waves (SSAW). Lab Chip 2009, 9, 2890–2895.
  120. Kothapalli, S.V.V.N.; Wiklund, M.; Janerot-Sjoberg, B.; Paradossi, G.; Grishenkov, D. Investigation of polymer-shelled microbubble motions in acoustophoresis. Ultrasonics 2016, 70, 275–283.
  121. Cushing, K.W.; Piyasena, M.E.; Carroll, N.J.; Maestas, G.C.; López, B.A.; Edwards, B.S.; Graves, S.W.; López, G.P. Elastomeric Negative Acoustic Contrast Particles for Affinity Capture Assays. Anal. Chem. 2013, 85, 2208–2215.
  122. Saito, M.; Itagaki, K.; Hayashi, K.; Tsubata, K. Composite Materials with Ultrasonically Induced Layer or Lattice Structure. Jpn. J. Appl. Phys. 1999, 38, 3028.
  123. Saito, M.; Imanishi, Y. Host-guest composites containing ultrasonically arranged particles. J. Mater. Sci. 2000, 35, 2373–2377.
  124. Saito, M.; Daian, T.; Hayashi, K.; Izumida, S.-Y. Fabrication of a polymer composite with periodic structure by the use of ultrasonic waves. J. Appl. Phys. 1998, 83, 3490–3494.
  125. Mitri, F.G.; Garzon, F.H.; Sinha, D.N. Characterization of acoustically engineered polymer nanocomposite metamaterials using x-ray microcomputed tomography. Rev. Sci. Instrum. 2011, 82, 034903.
  126. Melde, K.; Mark, A.G.; Qiu, T.; Fischer, P. Holograms for acoustics. Nature 2016, 537, 518–522.
  127. Zhang, J.; Yang, Y.; Zhu, B.; Li, X.; Jin, J.; Chen, Z.; Chen, Y.; Zhou, Q. Multifocal point beam forming by a single ultrasonic transducer with 3D printed holograms. Appl. Phys. Lett. 2018, 113, 243502.
  128. Melde, K.; Choi, E.; Wu, Z.; Palagi, S.; Qiu, T.; Fischer, P. Acoustic Fabrication via the Assembly and Fusion of Particles. Adv. Mater. 2018, 30.
  129. Collino, R.R.; Ray, T.R.; Fleming, R.C.; Cornell, J.D.; Compton, B.G.; Begley, M.R. Deposition of ordered two-phase materials using microfluidic print nozzles with acoustic focusing. Extreme Mech. Lett. 2016, 8, 96–106.
  130. Xu, F.; Finley, T.D.; Turkaydin, M.; Sung, Y.; Gurkan, U.A.; Yavuz, A.S.; Guldiken, R.O.; Demirci, U. The assembly of cell-encapsulating microscale hydrogels using acoustic waves. Biomaterials 2011, 32, 7847–7855.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
This entry is offline, you can click here to edit this entry!
Video Production Service
Feedback